Феномен Гиббса
В математике феномен Гиббса представляет собой колебательное поведение ряда Фурье кусочно - непрерывно дифференцируемой периодической функции вокруг скачка . й частичный ряд Фурье функции ( суммированием образованный самые низкие составляющие синусоиды ряда Фурье функции) создают большие пики вокруг скачка, которые выходят за пределы или занижают значения функции. По мере использования большего количества синусоидов эта ошибка аппроксимации приближается к пределу примерно в 9% скачка, хотя сумма бесконечного Фурье ряда в конечном итоге сходится почти везде (поточечная сходимость в непрерывных точках), за исключением точек разрыва. [1]
Явление Гиббса наблюдали физики-экспериментаторы и считали, что оно вызвано несовершенством измерительной аппаратуры. [2] но на самом деле это математический результат. Это одна из причин появления артефактов при обработке сигналов . Он назван в честь Джозайи Уилларда Гиббса .
Описание [ править ]


Феномен Гиббса представляет собой поведение ряда Фурье функции со скачком и описывается следующим образом:
По мере того, как берется больше составляющих или компонентов ряда Фурье, ряд Фурье показывает первый выброс в колебательном поведении вокруг точки скачка, приближающийся к ~ 9% от (полного) скачка, и это колебание не исчезает, а приближается к точке, так что интеграл колебаний стремится к нулю.
В точке перехода ряд Фурье дает среднее значение обеих сторон функции, приближающихся к этой точке.
Пример прямоугольной волны [ править ]
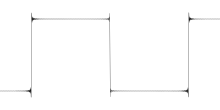
Три изображения справа демонстрируют явление Гиббса для прямоугольной волны (с размахом амплитуды от к и периодичность ) чей й частичный ряд Фурье
где . Точнее, эта прямоугольная волна представляет собой функцию что равно между и и между и для каждого целого числа ; таким образом, эта прямоугольная волна имеет скачок размаха высоты. для каждого целого числа, кратного .
По мере добавления большего количества синусоидальных членов (т. е. увеличения ), ошибка частного ряда Фурье сходится к фиксированной высоте. Но поскольку ширина ошибки продолжает сужаться, площадь ошибки – и, следовательно, энергия ошибки – стремится к 0. [3] Анализ прямоугольных волн показывает, что ошибка превышает высоту (от нуля). прямоугольной волны
или около 9% полного прыжка . В более общем смысле, при любом разрыве кусочно-непрерывно дифференцируемой функции со скачком , й частичный ряд Фурье функции будет (для очень большого значение) превысит этот скачок на ошибку, приближающуюся к на одном конце и на столько же ниже его на другом конце; таким образом, «полный скачок» в частичном ряду Фурье будет примерно на 18% больше, чем полный скачок в исходной функции. На разрыве частичный ряд Фурье будет сходиться к середине скачка (независимо от действительного значения исходной функции на разрыве) как следствие теоремы Дирихле . [4] Количество
История [ править ]
Феномен Гиббса был впервые замечен и проанализирован Генри Уилбрахамом в статье 1848 года. [6] Эта статья не привлекала особого внимания до 1914 года, когда она была упомянута в Генриха Буркхарда обзоре математического анализа в энциклопедии Кляйна . [7] В 1898 году Альберт А. Майкельсон разработал устройство, которое могло вычислять и повторно синтезировать ряд Фурье. [8] Широко распространен миф, согласно которому, когда в машину вводились коэффициенты Фурье для прямоугольной волны, график колебался на разрывах, и что, поскольку это было физическое устройство, подверженное производственным дефектам, Майкельсон был убежден, что перерегулирование было вызвано ошибками. в машине. На самом деле графики, созданные машиной, были недостаточно хороши, чтобы ясно продемонстрировать феномен Гиббса, и Майкельсон, возможно, не заметил этого, поскольку он не упомянул об этом эффекте в своей статье ( Michelson & Stratton 1898 ) о своей машине или в своих более поздних письмах. к Природе . [9]
Вдохновленный перепиской в журнале Nature между Майкельсоном и А.Э. Лавом о сходимости ряда Фурье прямоугольной волновой функции, Дж. Уиллард Гиббс опубликовал в 1898 году заметку, в которой указывалось на важное различие между пределом графиков частичных сумм функции Фурье. ряд пилообразной волны и график предела этих частичных сумм. В своем первом письме Гиббс не заметил феномена Гиббса, а предел, который он описал для графиков частичных сумм, был неточным. В 1899 году он опубликовал поправку, в которой описал выброс в точке разрыва ( «Nature» , 27 апреля 1899, стр. 606). В 1906 году Максим Боше дал подробный математический анализ этого превышения, введя термин «феномен Гиббса». [10] и ввести его в широкое применение. [9]
После того, как о существовании Генри Уилбрахама статьи стало широко известно, в 1925 году Горацио Скотт Карслоу заметил: «Мы все еще можем называть это свойство ряда Фурье (и некоторых других рядов) феноменом Гиббса; но мы больше не должны утверждать, что это свойство было впервые обнаружен Гиббсом». [11]
Объяснение [ править ]
Неформально феномен Гиббса отражает трудность, связанную с приближением функции конечной разрывной серией непрерывных синусоидальных волн. Важно сделать акцент на слове «конечный» , потому что, хотя каждая частичная сумма ряда Фурье выходит за пределы каждого аппроксимируемого разрыва, предел суммирования бесконечного числа синусоидальных волн этого не делает. Пики перерегулирования перемещаются все ближе и ближе к разрыву по мере суммирования большего количества членов, поэтому сходимость возможна.
Противоречия нет (между ошибкой выброса, стремящейся к ненулевой высоте, даже если бесконечная сумма не имеет выброса), поскольку пики выброса движутся в сторону разрыва. Таким образом, явление Гиббса демонстрирует поточечную , но не равномерную сходимость . Для кусочно- непрерывно дифференцируемого (класс C 1 ) функции ряд Фурье сходится к функции в каждой точке, кроме скачкообразных разрывов. При разрывах скачка бесконечная сумма будет сходиться к средней точке разрыва скачка (т. е. к среднему значению функции по обе стороны от скачка), как следствие теоремы Дирихле . [4]
Феномен Гиббса тесно связан с принципом, согласно которому гладкость функции контролирует скорость убывания ее коэффициентов Фурье. Коэффициенты Фурье более гладких функций будут затухать быстрее (что приводит к более быстрой сходимости), тогда как коэффициенты Фурье разрывных функций будут затухать медленно (что приводит к более медленной сходимости). Например, прерывистая прямоугольная волна имеет коэффициенты Фурье который распадается только со скоростью , а непрерывная треугольная волна имеет коэффициенты Фурье которые распадаются с гораздо большей скоростью .
Это лишь частично объясняет феномен Гиббса, поскольку ряды Фурье с абсолютно сходящимися коэффициентами Фурье будут равномерно сходиться по М-критерию Вейерштрасса и, следовательно, не смогут демонстрировать описанное выше колебательное поведение. Точно так же разрывная функция не может иметь абсолютно сходящиеся коэффициенты Фурье, поскольку, таким образом, функция была бы равномерным пределом непрерывных функций и, следовательно, была бы непрерывной, противоречие. См. Сходимость рядов Фурье § Абсолютная сходимость .
Решения [ править ]
Поскольку феномен Гиббса возникает из-за недолета, его можно устранить, используя ядра, которые никогда не бывают отрицательными, например ядро Фейера . [12] [13]
На практике трудности, связанные с явлением Гиббса, можно уменьшить, используя более гладкий метод суммирования рядов Фурье, такой как суммирование Фейера или суммирование Рисса , или используя сигма-аппроксимацию . При использовании непрерывного вейвлет- преобразования вейвлет-феномен Гиббса никогда не превосходит феномен Фурье-Гиббса. [14] Кроме того, при использовании дискретного вейвлет-преобразования с базисными функциями Хаара явление Гиббса вообще не возникает в случае непрерывных данных на скачкообразных разрывах, [15] и минимальна в дискретном случае в больших точках изменения. В вейвлет-анализе это обычно называют феноменом Лонго . В настройке полиномиальной интерполяции явление Гиббса можно смягчить с помощью алгоритма S-Гиббса. [16]
феномена Формальное математическое описание Гиббса
Позволять — кусочно- непрерывно дифференцируемая функция, периодическая с некоторым периодом . Предположим, что в какой-то момент , левый предел и правый предел функции отличаются ненулевым скачком :
Для каждого положительного целого числа ≥ 1, пусть быть й частичный ряд Фурье ( можно рассматривать как математический оператор над функциями.)
где коэффициенты Фурье для целых чисел задаются обычными формулами
Тогда у нас есть
В более общем смысле, если любая последовательность действительных чисел, сходящаяся к как , а если скачок тогда положительно
Если вместо этого прыжок отрицательно, необходимо поменять местами верхний предел ( ) с меньшим пределом ( ), а также поменять местами и знаки в двух приведенных выше неравенствах.
Доказательство явления Гиббса в общем случае [ править ]
Еще раз повторюсь, пусть — кусочно-непрерывно дифференцируемая функция, периодическая с некоторым периодом , и эта функция имеет несколько точек разрыва скачка, обозначенных где и так далее. На каждом разрыве величина вертикального полного прыжка равна .
Затем, можно выразить как сумму непрерывной функции и многоступенчатая функция которая представляет собой сумму ступенчатых функций, таких как [17]
как й частичный ряд Фурье вообще хорошо сойдутся точки, кроме точек вблизи разрывов . Вокруг каждой точки разрыва , будет иметь только свой феномен Гиббса (максимальная ошибка колебательной сходимости ~9% от скачка , как показано в анализе прямоугольных волн ), поскольку другие функции непрерывны ( ) или плоский ноль ( где ) около этой точки. Это доказывает, что феномен Гиббса возникает на каждом разрыве.
Объяснение обработки сигналов [ править ]

С обработки сигналов точки зрения явление Гиббса — это переходная характеристика фильтра нижних частот , а колебания называются звонкими или звонкими артефактами . Усечение преобразования Фурье сигнала на реальной линии или ряда Фурье периодического сигнала (эквивалентно сигналу на круге) соответствует фильтрации более высоких частот с помощью идеального ( кирпичного ) фильтра нижних частот. Это можно представить как свертку исходного сигнала с импульсной характеристикой фильтра (также известного как ядро ), которая является функцией sinc . Таким образом, феномен Гиббса можно рассматривать как результат свертки ступенчатой функции Хевисайда (если периодичность не требуется) или прямоугольной волны (если периодичность) с функцией sinc: колебания функции sinc вызывают пульсации на выходе.

В случае свертки со ступенчатой функцией Хевисайда результирующая функция представляет собой в точности интеграл от функции sinc, синусоидальный интеграл ; для прямоугольной волны описание не так просто. Таким образом, для ступенчатой функции величина отклонения равна точно интегралу от левого хвоста до первого отрицательного нуля: для нормализованного синуса единичного периода выборки это Соответственно, выброс имеет ту же самую величину: интеграл правого хвоста или (что эквивалентно) разницу между интегралом от отрицательной бесконечности до первого положительного нуля минус 1 (значение невылета).
Перелет и недолет можно понимать следующим образом: ядра обычно нормализуются так, чтобы иметь интеграл 1, поэтому они приводят к отображению постоянных функций в постоянные функции - в противном случае они имеют коэффициент усиления . Значение свертки в точке представляет собой линейную комбинацию входного сигнала с коэффициентами (весами) и значениями ядра.
Если ядро неотрицательно, например, для ядра Гаусса , то значение отфильтрованного сигнала будет выпуклой комбинацией входных значений (коэффициенты (ядро) интегрируются до 1 и неотрицательны), и таким образом, будет находиться между минимумом и максимумом входного сигнала – он не будет ниже или выше нормы. Если, с другой стороны, ядро принимает отрицательные значения, такие как функция sinc, тогда значение отфильтрованного сигнала вместо этого будет аффинной комбинацией входных значений и может выходить за пределы минимума и максимума входного сигнала. что приводит к недорегулированию и перерегулированию, как в феномене Гиббса.
Более длительное расширение – резка на более высокой частоте – соответствует в частотной области расширению кирпичной стены, что во временной области соответствует сужению функции sinc и увеличению ее высоты в тот же раз, оставляя интегралы между соответствующими точками неизменными. . Это общая особенность преобразования Фурье: расширение в одной области соответствует сужению и увеличению высоты в другой. Это приводит к тому, что колебания в sinc становятся уже и выше, и (в отфильтрованной функции после свертки) дают колебания, которые уже (и, следовательно, с меньшей площадью ), но не имеют уменьшенной величины : отсечение на любой конечной частоте приводит к функция sinc, какой бы узкой она ни была, с теми же хвостовыми интегралами. Это объясняет постоянство перерегулирования и недорегулирования.
- Колебания можно интерпретировать как свертку с синком.
- Более высокая отсечка делает синк уже, но выше, с хвостовыми интегралами той же величины, что приводит к колебаниям более высокой частоты, но величина которых не исчезает.
Таким образом, особенности феномена Гиббса интерпретируются следующим образом:
- недолет обусловлен тем, что импульсная характеристика имеет отрицательный хвостовой интеграл, что возможно, поскольку функция принимает отрицательные значения;
- перерегулирование компенсирует это за счет симметрии (общий интеграл не меняется при фильтрации);
- сохранение колебаний связано с тем, что увеличение отсечки сужает импульсную характеристику, но не уменьшает ее интеграл – колебания при этом движутся в сторону разрыва, но не уменьшаются по величине.
Анализ прямоугольных волн [ править ]

Мы рассматриваем й частичный ряд Фурье прямоугольной волны с периодичностью и прерывистость вертикального "полного" прыжка от в . Поскольку случай нечетного очень похоже, давайте просто рассмотрим случай, когда четный:
с . ( где - это количество ненулевых синусоидальных компонентов ряда Фурье, поэтому в литературе используется вместо .) Замена (точка разрыва), получаем
Далее находим первый максимум колебания вокруг разрыва проверив первую и вторую производные . Первое условие максимума состоит в том, что первая производная равна нулю при
где 2-е равенство взято из одного из тригонометрических тождеств Лагранжа . Решение этого условия дает для целых чисел исключая кратные чтобы избежать нулевого знаменателя, поэтому и их негативы разрешены.
Вторая производная от в является
Таким образом, первый максимум имеет место при ( ) и в этом значение
Если мы введем нормализованную функцию sinc для , мы можем переписать это как
Для достаточно большого выражение в квадратных скобках представляет собой приближение суммы Римана к интегралу (точнее, это аппроксимация правила средней точки с интервалом ). Поскольку функция sinc непрерывна, это приближение сходится к интегралу как . Таким образом, мы имеем
о чем говорилось в предыдущем разделе. Аналогичный расчет показывает
Последствия [ править ]
Феномен Гиббса нежелателен, поскольку он вызывает артефакты, а именно отсечение от перерегулирования и недорегулирования, а также звенящие артефакты от колебаний. В случае фильтрации нижних частот их можно уменьшить или устранить с помощью различных фильтров нижних частот.
В МРТ феномен Гиббса вызывает артефакты при наличии соседних областей с заметно отличающейся интенсивностью сигнала. Это чаще всего встречается при МРТ позвоночника, где феномен Гиббса может имитировать появление сирингомиелии .
Феномен Гиббса проявляется в виде артефакта перекрестного узора в дискретном преобразовании Фурье изображения. [18] где большинство изображений (например, микрофотографий или фотографий) имеют резкий разрыв между границами сверху/снизу и слева/справа изображения. Когда в преобразовании Фурье накладываются периодические граничные условия, этот скачок разрыва представляется континуумом частот вдоль осей в обратном пространстве (т.е. перекрестной картиной интенсивности в преобразовании Фурье).
И хотя эта статья в основном сосредоточена на сложности попыток построить разрывы без артефактов во временной области с помощью только частичного ряда Фурье, важно также учитывать, что, поскольку обратное преобразование Фурье чрезвычайно похоже на преобразование Фурье , существует эквивалентное сложность с попыткой построить разрывы в частотной области, используя только частичный ряд Фурье. Так, например, поскольку идеализированные кирпичные и прямоугольные фильтры имеют разрывы в частотной области , их точное представление во временной области обязательно требует бесконечно длинной импульсной характеристики синхрофильтра , поскольку конечная импульсная характеристика приведет к пульсациям Гиббса в частотной характеристике. вблизи частот среза , хотя эту пульсацию можно уменьшить с помощью оконных фильтров с конечной импульсной характеристикой (за счет более широких полос перехода). [19]
См. также [ править ]
- Полосы Маха
- Феномен Пински
- Феномен Рунге (аналогичное явление в полиномиальных приближениях)
- σ-аппроксимация , которая корректирует суммирование Фурье для устранения явления Гиббса, которое в противном случае возникало бы на разрывах.
- Синусоидальный интеграл
Примечания [ править ]
- ^ Х. С. Карслоу (1930). «Глава IX» . Введение в теорию рядов и интегралов Фурье (Третье изд.). Нью-Йорк: Dover Publications Inc.
- ^ Вретблад 2000 Раздел 4.7.
- ^ «6.7: Феномены Гиббса» . Инженерные библиотеки LibreTexts . 24 мая 2020 г. Проверено 3 марта 2022 г.
- ^ Jump up to: а б М. Пинский (2002). Введение в анализ Фурье и вейвлеты . Соединенные Штаты Америки: Брукс/Коул. п. 27 .
- ^ Стивен Р. Финч, Математические константы , Cambridge University Press, 2003, раздел 4.1 Константа Гиббса-Уилбрахама, стр. 249.
- ^ Уилбрахам, Генри (1848) «Об некоторой периодической функции» , Кембриджский и Дублинский математический журнал , 3 : 198–201.
- ^ Энциклопедия математических наук, включая их приложения (PDF) . Том II Т. 1 H 1. Висбаден: Vieweg + Teubner Verlag. 1914. с. 1049 . Проверено 14 сентября 2016 г.
- ^ Хаммак, Билл; Кранц, Стив; Карпентер, Брюс (29 октября 2014 г.). Гармонический анализатор Альберта Майкельсона: визуальный обзор машины девятнадцатого века, выполняющей анализ Фурье . Книги по шарнирному шуму. ISBN 9780983966173 . Проверено 14 сентября 2016 г.
- ^ Jump up to: а б Хьюитт, Эдвин; Хьюитт, Роберт Э. (1979). «Феномен Гиббса-Уилбрахама: эпизод анализа Фурье». Архив истории точных наук . 21 (2): 129–160. дои : 10.1007/BF00330404 . S2CID 119355426 . Доступно онлайн по адресу: Национальный университет Цзяо Дун: Open Course Ware: Hewitt & Hewitt, 1979. Архивировано 4 марта 2016 г. в Wayback Machine.
- ^ Боше, Максим (апрель 1906 г.) «Введение в теорию рядов Фурье» , Annals of Mathematics , вторая серия, 7 (3): 81–152. Феномен Гиббса обсуждается на страницах 123–132; Роль Гиббса упомянута на странице 129.
- ^ Карслоу, HS (1 октября 1925 г.). «Историческая справка о явлении Гиббса в рядах и интегралах Фурье» . Бюллетень Американского математического общества . 31 (8): 420–424. дои : 10.1090/s0002-9904-1925-04081-1 . ISSN 0002-9904 . Проверено 14 сентября 2016 г.
- ^ Готлиб, Дэвид; Шу, Чи-Ван (январь 1997 г.). «О феномене Гиббса и его разрешении» . Обзор СИАМ . 39 (4): 644–668. дои : 10.1137/S0036144596301390 . ISSN 0036-1445 .
- ^ Готлиб, Сигал; Юнг, Джэ-Хун; Ким, Саеджа (март 2011 г.). «Обзор работы Дэвида Готлиба по разрешению феномена Гиббса» . Коммуникации в вычислительной физике . 9 (3): 497–519. дои : 10.4208/cicp.301109.170510s . ISSN 1815-2406 .
- ^ Расмуссен, Хенрик О. «Феномен вейвлета Гиббса». В книге «Вейвлеты, фракталы и преобразования Фурье» , Эдс М. Фардж и др., Clarendon Press, Оксфорд, 1993.
- ^ Сьюзен Э., Келли (1995). «Феномен Гиббса для вейвлетов» (PDF) . Прикладной и вычислительный гармонический анализ (3). Архивировано из оригинала (PDF) 9 сентября 2013 г. Проверено 31 марта 2012 г.
- ^ Де Марки, Стефано; Маркетти, Франческо; Перраккьоне, Эмма; Поджиали, Давиде (2020). «Полиномиальная интерполяция через сопоставленные базы без повторной выборки» . Дж. Компьютер. Прил. Математика . 364 : 112347. doi : 10.1016/j.cam.2019.112347 . ISSN 0377-0427 . S2CID 199688130 .
- ^ Фэй, Темпл Х.; Клопперс, П. Хендрик (2001). «Феномен Гиббса» . Международный журнал математического образования в области науки и технологий . 32 (1): 73–89. дои : 10.1080/00207390117151 .
- ^ Р. Ховден, Ю. Цзян, Х. Л. Синь, Л. Ф. Куркутис (2015). «Периодическое уменьшение артефактов при преобразовании Фурье изображений с полным полем атомного разрешения» . Микроскопия и микроанализ . 21 (2): 436–441. arXiv : 2210.09024 . дои : 10.1017/S1431927614014639 . ПМИД 25597865 . S2CID 22435248 .
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ «Феномен Гиббса | Блоги звукозаписи» . www.recordingblogs.com . Проверено 5 марта 2022 г.
Ссылки [ править ]
- Гиббс, Дж. Уиллард (1898), «Серия Фурье» , Nature , 59 (1522): 200, doi : 10.1038/059200b0 , ISSN 0028-0836 , S2CID 4004787
- Гиббс, Дж. Уиллард (1899), «Серия Фурье», Nature , 59 (1539): 606, doi : 10.1038/059606a0 , ISSN 0028-0836 , S2CID 13420929
- Майкельсон, А.А.; Страттон, SW (1898), «Новый гармонический анализатор», Philosophical Magazine , 5 (45): 85–91.
- Зигмунд, Антони (1959). Тригонометрическая серия (2-е изд.). Издательство Кембриджского университета. Том 1 , Том 2 .
- Уилбрахам, Генри (1848), «Об некоторой периодической функции» , Кембриджский и Дублинский математический журнал , 3 : 198–201.
- Пол Дж. Нахин , Невероятная формула доктора Эйлера, Princeton University Press, 2006. Гл. 4, разд. 4.
- Вретблад, Андерс (2000), Анализ Фурье и его приложения , Тексты для аспирантов по математике, том. 223, Нью-Йорк: Springer Publishing , с. 93, ISBN 978-0-387-00836-3
Внешние ссылки [ править ]
 СМИ, связанные с феноменом Гиббса, на Викискладе?
СМИ, связанные с феноменом Гиббса, на Викискладе? - «Феномен Гиббса» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Вайсштейн, Эрик В., « Феномен Гиббса ». Из MathWorld — веб-ресурса Wolfram.
- Прандони, Паоло, « Феномен Гиббса ».
- Радаелли-Санчес, Рикардо и Ричард Баранюк, « Феномен Гиббса ». Проект «Связи». (Лицензия Creative Commons с указанием авторства)
- Горацио С. Карслоу: Введение в теорию рядов Фурье и интегралов.pdf (introductiontot00unkngoog.pdf) на archive.org
- Реализация на Python, алгоритма S-Гиббса смягчающая феномен Гиббса https://github.com/pog87/FakeNodes .

















































































![{\displaystyle \left.{\frac {d^{2}}{dx^{2}}}S_{N}f(x)\right\vert _{x_{0}+kL/(2N)}= {\begin{cases}{\frac {2c}{L}}{\frac {N}{\sin(k\pi /N)}},&{\text{if }}k{\text{ четно ,}}\\[4pt]{\frac {2c}{L}}{\frac {-N}{\sin(k\pi /N)}},&{\text{if }}k{\text { нечетно.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24bbc8762a7e3685fb6fa1e88672c4a4a610d30)





![{\displaystyle S_{N}f\left(x_{0}+{\frac {L}{2N}}\right)=(y_{0}+{\frac {c}{2}})+c\ left[{\frac {2}{N}}\operatorname {sinc} \left({\frac {1}{N}}\right)+{\frac {2}{N}}\operatorname {sinc} \ left({\frac {3}{N}}\right)+\cdots +{\frac {2}{N}}\operatorname {sinc} \left({\frac {(N-1)}{N} }\вправо)\вправо].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6a4711017c14b1447fe200ddc1f2206bebb38b0)



![{\displaystyle {\begin{aligned}\lim _{N\to \infty }S_{N}f\left(x_{0}+{\frac {L}{2N}}\right)&=(y_{ 0}+{\frac {c}{2}})+c\int _{0}^{1}\operatorname {sinc} (x)\,dx\\[8pt]&=(y_{0}+ {\frac {c}{2}})+{\frac {c}{\pi }}\int _{x=0}^{1}{\frac {\sin(\pi x)}{\pi x}}\,d(\pi x)\\[8pt]&=(y_{0}+{\frac {c}{2}})+{\frac {c}{\pi }}\int _ {0}^{\pi }{\frac {\sin(t)}{t}}\ dt\quad =\quad (y_{0}+c)+c\cdot (0.089489872236\dots ),\end{ выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a6af86b733c782cf1f4cfc6fb4200e73cb172e5)
