Равномерная сходимость

Последовательность функций (fₙ) сходится равномерно к f, когда для любого малого ε существует индекс N такой, что график fₙ находится в ε-трубке вокруг f всякий раз, когда n ≥ N.

В математической области анализа поточечная равномерная сходимость — это более сильный способ сходимости функций, чем сходимость . Последовательность ​ функций ​ $(f_{n})$ сходится равномерно к предельной функции $f$ на съемочной площадке $E$ как область определения функции, если для любого сколь угодно малого положительного числа $\epsilon$, число $N$ можно найти так, что каждая из функций $f_{N},f_{N+1},f_{N+2},\ldots$ отличается от $f$ не более чем $\epsilon$ в каждой точке $x$ в $E$. Описывается неформально, если $f_{n}$ сходится к $f$ равномерно, то как быстро функции $f_{n}$ подход $f$ является «однородным» во всем $E$ в следующем смысле: чтобы гарантировать, что $f_{n}(x)$ отличается от $f(x)$ меньше выбранного расстояния $\epsilon$, нам нужно только убедиться, что $n$ больше или равно определенному $N$, который мы можем найти, не зная значения $x\in E$ заранее. Другими словами, существует число $N=N(\epsilon )$ это может зависеть от $\epsilon$ но не зависит от $x$, такой, что выбирая $n\geq N$ будет гарантировать, что $|f_{n}(x)-f(x)|<\epsilon$ для всех $x\in E$. Напротив, поточечная сходимость $f_{n}$ к $f$ просто гарантирует, что для любого $x\in E$ задано заранее, мы можем найти $N=N(\epsilon ,x)$ (т.е. $N$ может зависеть от значений обоих $\epsilon$ и $x$) такой, что для этого конкретного $x$, $f_{n}(x)$ попадает в пределах $\epsilon$ из $f(x)$ в любое время $n\geq N$ (и другое $x$ может потребоваться другой, более крупный $N$ для $n\geq N$ чтобы гарантировать это $|f_{n}(x)-f(x)|<\epsilon$).

Разница между равномерной и поточечной сходимостью не была полностью осознана на ранних этапах истории исчисления, что приводило к случаям ошибочных рассуждений. Концепция, которая была впервые формализована Карлом Вейерштрассом , важна тем, что некоторые свойства функций $f_{n}$, такие как непрерывность , интегрируемость по Риману и, при дополнительных гипотезах, дифференцируемость , переводятся в предел $f$ если сходимость равномерная, но не обязательно, если сходимость неравномерная.

История

В 1821 году Огюстен-Луи Коши опубликовал доказательство того, что сходящаяся сумма непрерывных функций всегда непрерывна, чему Нильс Хенрик Абель в 1826 году нашел предполагаемые контрпримеры в контексте рядов Фурье , утверждая, что доказательство Коши должно быть неверным. В то время не существовало совершенно стандартных представлений о сходимости, и Коши решал сходимость, используя методы бесконечно малых величин. Говоря современным языком, Коши доказал, что равномерно сходящаяся последовательность непрерывных функций имеет непрерывный предел. Неспособность просто поточечно сходящегося предела непрерывных функций сходиться к непрерывной функции иллюстрирует важность различия между различными типами сходимости при работе с последовательностями функций.

Термин «равномерная сходимость», вероятно, впервые был использован Кристофом Гудерманом в статье 1838 года об эллиптических функциях , где он использовал фразу «сходимость равномерным образом», когда «способ сходимости» ряда ${\textstyle \sum _{n=1}^{\infty }f_{n}(x,\phi ,\psi )}$ не зависит от переменных $\phi$ и $\psi .$ Хотя он считал сходимость ряда таким образом «замечательным фактом», он не дал формального определения и не использовал это свойство ни в одном из своих доказательств.

Позже ученик Гудермана Карл Вейерштрасс , посещавший его курс эллиптических функций в 1839–1840 годах, ввёл термин gleichmäßig konvergent ( нем .: равномерно сходящийся ), который он использовал в своей статье 1841 года «Zur Theorie der Potenzreihen» , опубликованной в 1894 году. сформулировано Филиппом Людвигом фон Зейделем и Джордж Габриэль Стоукс . Г.Х. Харди сравнивает три определения в своей статье «Сэр Джордж Стоукс и концепция равномерной сходимости» и отмечает: «Открытие Вейерштрасса было самым ранним, и только он один полностью осознал его далеко идущее значение как одной из фундаментальных идей анализа».

Под влиянием Вейерштрасса и Бернхарда Римана это понятие и связанные с ним вопросы интенсивно изучались в конце XIX века Германом Ханкелем , Полем дю Буа-Реймоном , Улиссом Дини , Чезаре Арзела и другими.

Определение

Сначала мы определяем равномерную сходимость для вещественнозначных функций , хотя эту концепцию легко обобщить на функции, отображающиеся в метрические пространства и, в более общем смысле, в равномерные пространства (см. ниже ).

Предполагать $E$ представляет собой набор и $(f_{n})_{n\in \mathbb {N} }$ представляет собой последовательность вещественных функций на нем. Мы говорим последовательность $(f_{n})_{n\in \mathbb {N} }$ сходится равномерно на $E$ с лимитом $f:E\to \mathbb {R}$ если для каждого $\epsilon >0,$ существует натуральное число $N$ такой, что для всех $n\geq N$ и для всех $x\in E$

$|f_{n}(x)-f(x)|<\epsilon .$

Обозначение равномерной сходимости $f_{n}$ к $f$ не совсем стандартизирован, и разные авторы использовали различные символы, в том числе (примерно в порядке убывания популярности):

$f_{n}\rightrightarrows f,\quad {\underset {n\to \infty }{\mathrm {unif\ lim} }}f_{n}=f,\quad f_{n}{\overset {\mathrm {unif.} }{\longrightarrow }}f,\quad f=\mathrm {u} \!\!-\!\!\!\lim _{n\to \infty }f_{n}.$

Часто специальный символ не используется, а авторы просто пишут

$f_{n}\to f\quad \mathrm {uniformly}$

чтобы указать, что сходимость равномерна. (Напротив, выражение $f_{n}\to f$ на $E$ без наречия понимается как поточечная сходимость на $E$: для всех $x\in E$, $f_{n}(x)\to f(x)$ как $n\to \infty$.)

С $\mathbb {R}$ является полным метрическим пространством , критерий Коши можно использовать для получения эквивалентной альтернативной формулировки равномерной сходимости: $(f_{n})_{n\in \mathbb {N} }$ сходится равномерно на $E$ (в предыдущем смысле) тогда и только тогда, когда для каждого $\epsilon >0$, существует натуральное число $N$ такой, что

$x\in E,m,n\geq N\implies |f_{m}(x)-f_{n}(x)|<\epsilon$.

В еще одной эквивалентной формулировке, если мы определим

$d_{n}=\sup _{x\in E}|f_{n}(x)-f(x)|,$

затем $f_{n}$ сходится к $f$ равномерно тогда и только тогда, когда $d_{n}\to 0$ как $n\to \infty$. Таким образом, мы можем охарактеризовать равномерную сходимость $(f_{n})_{n\in \mathbb {N} }$ на $E$ как (простая) сходимость $(f_{n})_{n\in \mathbb {N} }$ в функциональном пространстве $\mathbb {R} ^{E}$ относительно равномерной метрики (также называемой супремум -метрикой), определяемой формулой

$d(f,g)=\sup _{x\in E}|f(x)-g(x)|.$

Символически,

$f_{n}\rightrightarrows f\iff d(f_{n},f)\to 0$.

Последовательность $(f_{n})_{n\in \mathbb {N} }$ называется локально равномерно сходящимся с пределом $f$ если $E$ является метрическим пространством и для каждого $x\in E$, существует $r>0$ такой, что $(f_{n})$ сходится равномерно на $B(x,r)\cap E.$ Ясно, что равномерная сходимость влечет за собой локальную равномерную сходимость, а значит, и поточечную сходимость.

Примечания

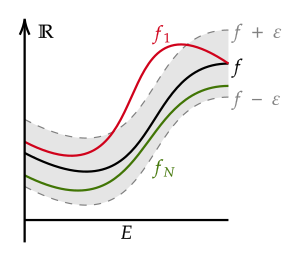
Интуитивно последовательность функций $f_{n}$ сходится равномерно к $f$ если при сколь угодно малом $\epsilon >0$, мы можем найти $N\in \mathbb {N}$ так что функции $f_{n}$ с $n>N$ все попадает в «трубку» по ширине $2\epsilon$ сосредоточен вокруг $f$ (т.е. между $f(x)-\epsilon$ и $f(x)+\epsilon$) для всей области определения функции.

Обратите внимание, что замена порядка кванторов в определении равномерной сходимости путем перемещения «для всех $x\in E$"перед "существует натуральное число $N$" приводит к определению поточечной сходимости последовательности. Чтобы сделать это различие явным, в случае равномерной сходимости: $N=N(\epsilon )$ может зависеть только от $\epsilon$, и выбор $N$ должен работать на всех $x\in E$, для определенного значения $\epsilon$ что дано. Напротив, в случае поточечной сходимости $N=N(\epsilon ,x)$ может зависеть от обоих $\epsilon$ и $x$, и выбор $N$ должен работать только для определенных значений $\epsilon$ и $x$ что дано. Таким образом, равномерная сходимость подразумевает поточечную сходимость, однако обратное неверно, как иллюстрирует пример в разделе ниже.

Обобщения

Эту концепцию можно напрямую распространить на функции E → M , где ( M , d ) — метрическое пространство , заменив $|f_{n}(x)-f(x)|$ с $d(f_{n}(x),f(x))$.

Наиболее общей постановкой является равномерная сходимость сетей функций E → X , где X — равномерное пространство . Мы говорим, что сеть $(f_{\alpha })$ сходится равномерно с пределом f : E → X тогда и только тогда, когда для любого окружения V в X существует $\alpha _{0}$, такой, что для каждого x в E и каждого $\alpha \geq \alpha _{0}$, $(f_{\alpha }(x),f(x))$ в В. находится В этой ситуации равномерный предел непрерывных функций остается непрерывным.

Определение в гиперреальной обстановке

Равномерная сходимость допускает упрощенное определение в гиперреальной среде. Таким образом, последовательность $f_{n}$ сходится к f равномерно, если для всех гипервещественных x в области $f^{*}$ и все бесконечные n , $f_{n}^{*}(x)$ бесконечно близок к $f^{*}(x)$ ( см. в разделе «Микронепрерывность аналогичное определение равномерной непрерывности »). Напротив, поточечная непрерывность требует этого только для вещественного x .

Примеры

Для $x\in [0,1)$, основной пример равномерной сходимости можно проиллюстрировать следующим образом: последовательность $(1/2)^{x+n}$ сходится равномерно, а $x^{n}$ нет. В частности, предположим $\epsilon =1/4$. Каждая функция $(1/2)^{x+n}$ меньше или равно $1/4$ когда $n\geq 2$, независимо от значения $x$. С другой стороны, $x^{n}$ только меньше или равно $1/4$ при постоянно возрастающих значениях $n$ когда значения $x$ выбираются все ближе и ближе к 1 (подробнее объясняется ниже).

Учитывая топологическое пространство X , мы можем снабдить пространство ограниченных действительных или комплекснозначных функций над X с топологией равномерной нормы равномерной метрикой, определяемой формулой

$d(f,g)=\|f-g\|_{\infty }=\sup _{x\in X}|f(x)-g(x)|.$

Тогда равномерная сходимость просто означает сходимость в топологии с равномерной нормой :

$\lim _{n\to \infty }\|f_{n}-f\|_{\infty }=0$.

Последовательность функций $(f_{n})$

${\begin{cases}f_{n}:[0,1]\to [0,1]\\f_{n}(x)=x^{n}\end{cases}}$

является классическим примером последовательности функций, сходящейся к функции $f$ точечно, но не равномерно. Чтобы показать это, сначала заметим, что поточечный предел $(f_{n})$ как $n\to \infty$ это функция $f$, заданный

$f(x)=\lim _{n\to \infty }f_{n}(x)={\begin{cases}0,&x\in [0,1);\\1,&x=1.\end{cases}}$

Поточечная сходимость: сходимость тривиальна для $x=0$ и $x=1$, с $f_{n}(0)=f(0)=0$ и $f_{n}(1)=f(1)=1$, для всех $n$. Для $x\in (0,1)$ и учитывая $\epsilon >0$, мы можем гарантировать, что $|f_{n}(x)-f(x)|<\epsilon$ в любое время $n\geq N$ выбрав $N=\lceil \log \epsilon /\log x\rceil$, который является минимальным целым показателем степени $x$ что позволяет ему достичь или опуститься ниже $\epsilon$ (здесь верхние квадратные скобки обозначают округление в большую сторону, см. функцию потолка ). Следовательно, $f_{n}\to f$ точечно для всех $x\in [0,1]$. Обратите внимание, что выбор $N$ зависит от стоимости $\epsilon$ и $x$. Более того, при фиксированном выборе $\epsilon$, $N$ (который нельзя определить как меньший) неограниченно растет как $x$ подходы 1. Эти наблюдения исключают возможность равномерной сходимости.

Неравномерность сходимости. Сходимость не является равномерной, поскольку мы можем найти $\epsilon >0$ так что независимо от того, насколько большой мы выберем $N,$ будут значения $x\in [0,1]$ и $n\geq N$ такой, что $|f_{n}(x)-f(x)|\geq \epsilon .$ Чтобы убедиться в этом, сначала заметим, что независимо от размера $n$ становится, всегда есть $x_{0}\in [0,1)$ такой, что $f_{n}(x_{0})=1/2.$ Таким образом, если мы выберем $\epsilon =1/4,$ мы никогда не сможем найти $N$ такой, что $|f_{n}(x)-f(x)|<\epsilon$ для всех $x\in [0,1]$ и $n\geq N$. Явно, какого бы кандидата мы ни выбрали $N$, рассмотрим значение $f_{N}$ в $x_{0}=(1/2)^{1/N}$. С

$\left|f_{N}(x_{0})-f(x_{0})\right|=\left|\left[\left({\frac {1}{2}}\right)^{\frac {1}{N}}\right]^{N}-0\right|={\frac {1}{2}}>{\frac {1}{4}}=\epsilon ,$

кандидат терпит неудачу, потому что мы нашли пример $x\in [0,1]$ что «ускользнуло» от нашей попытки «ограничить» каждого $f_{n}\ (n\geq N)$ внутри $\epsilon$ из $f$ для всех $x\in [0,1]$. На самом деле, это легко увидеть

$\lim _{n\to \infty }\|f_{n}-f\|_{\infty }=1,$

вопреки требованию, $\|f_{n}-f\|_{\infty }\to 0$ если $f_{n}\rightrightarrows f$.

На этом примере легко увидеть, что поточечная сходимость не сохраняет дифференцируемости и непрерывности. Хотя каждая функция последовательности является гладкой, то есть для n всех $f_{n}\in C^{\infty }([0,1])$, предел $\lim _{n\to \infty }f_{n}$ даже не является непрерывным.

Экспоненциальная функция

разложение показательной функции в ряд равномерно сходится на любом ограниченном подмножестве. Можно показать, что $S\subset \mathbb {C}$ с помощью М-теста Вейерштрасса .

Теорема (М-критерий Вейерштрасса). Позволять $(f_{n})$ быть последовательностью функций $f_{n}:E\to \mathbb {C}$ и пусть $M_{n}$ — последовательность положительных действительных чисел такая, что $|f_{n}(x)|\leq M_{n}$ для всех $x\in E$ и $n=1,2,3,\ldots$ Если ${\textstyle \sum _{n}M_{n}}$ сходится, то ${\textstyle \sum _{n}f_{n}}$ сходится абсолютно и равномерно на $E$.

Комплексную показательную функцию можно выразить в виде ряда:

$\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.$

Любое ограниченное подмножество является подмножеством некоторого диска $D_{R}$ радиуса $R,$ с центром в начале координат на комплексной плоскости . М-критерий Вейерштрасса требует от нас найти верхнюю границу $M_{n}$ по условиям сериала, с $M_{n}$ независимо от положения на диске:

$\left|{\frac {z^{n}}{n!}}\right|\leq M_{n},\forall z\in D_{R}.$

Для этого замечаем

$\left|{\frac {z^{n}}{n!}}\right|\leq {\frac {|z|^{n}}{n!}}\leq {\frac {R^{n}}{n!}}$

и возьми $M_{n}={\tfrac {R^{n}}{n!}}.$

Если $\sum _{n=0}^{\infty }M_{n}$ сходится, то M-тест утверждает, что исходный ряд сходится равномерно.

тест соотношения Здесь можно использовать :

$\lim _{n\to \infty }{\frac {M_{n+1}}{M_{n}}}=\lim _{n\to \infty }{\frac {R^{n+1}}{R^{n}}}{\frac {n!}{(n+1)!}}=\lim _{n\to \infty }{\frac {R}{n+1}}=0$

а это значит, что сериал окончен $M_{n}$ является конвергентным. Таким образом, исходный ряд сходится равномерно для всех $z\in D_{R},$ и поскольку $S\subset D_{R}$, ряд также сходится равномерно на $S.$

Свойства

• Любая равномерно сходящаяся последовательность сходится локально равномерно.
• Любая локально равномерно сходящаяся последовательность компактно сходящаяся .
• Для локально компактных пространств локальная равномерная сходимость и компактная сходимость совпадают.
• Последовательность непрерывных функций на метрических пространствах с полным образом метрического пространства сходится равномерно тогда и только тогда, когда она равномерно Коши .
• Если $S$ является компактным интервалом (или, вообще, компактным топологическим пространством) и $(f_{n})$ представляет собой монотонно возрастающую последовательность (т.е. $f_{n}(x)\leq f_{n+1}(x)$ для всех n и x ) непрерывных функций с поточечным пределом $f$ которая также непрерывна, то сходимость обязательно равномерная ( теорема Дини ). Равномерная сходимость также гарантируется, если $S$ представляет собой компактный интервал и $(f_{n})$ — равнонепрерывная последовательность, сходящаяся поточечно.

Приложения

Чтобы преемственность

Основная статья: Равномерная предельная теорема

Контрпример к усилению теоремы о равномерной сходимости, в которой предполагается поточечная, а не равномерная сходимость. Непрерывные зеленые функции $\sin ^{n}(x)$ сходятся к прерывистой красной функции. Это может произойти только в том случае, если сходимость не является равномерной.

Если $E$ и $M$ являются топологическими пространствами , то имеет смысл говорить о непрерывности функций $f_{n},f:E\to M$. Если мы далее предположим, что $M$ — метрическое пространство , то (равномерная) сходимость $f_{n}$ к $f$ также четко определен. Следующий результат утверждает, что непрерывность сохраняется при равномерной сходимости:

Равномерная предельная теорема . Предположим, $E$ является топологическим пространством, $M$ является метрическим пространством, и $(f_{n})$ представляет собой последовательность непрерывных функций $f_{n}:E\to M$. Если $f_{n}\rightrightarrows f$ на $E$, затем $f$ также является непрерывным.

Эта теорема доказывается с помощью « трюка ε/3 » и является архетипическим примером этого трюка: для доказательства заданного неравенства ( ε ) используются определения непрерывности и равномерной сходимости, чтобы получить 3 неравенства ( ε/3 ), а затем объединяет их с помощью неравенства треугольника , чтобы получить желаемое неравенство.

Эта теорема является важной в истории вещественного анализа и анализа Фурье, поскольку многие математики XVIII века интуитивно понимали, что последовательность непрерывных функций всегда сходится к непрерывной функции. На изображении выше показан контрпример, и многие разрывные функции фактически могут быть записаны как ряды Фурье непрерывных функций. Ошибочное утверждение о том, что поточечный предел последовательности непрерывных функций непрерывен (первоначально сформулированное в терминах сходящихся рядов непрерывных функций), печально известно как «неправильная теорема Коши». Равномерная предельная теорема показывает, что для обеспечения сохранения непрерывности предельной функции необходима более сильная форма сходимости, равномерная сходимость.

Точнее, эта теорема утверждает, что равномерный предел равномерно непрерывных функций равномерно непрерывен; для локально компактного пространства непрерывность эквивалентна локальной равномерной непрерывности, и, следовательно, равномерный предел непрерывных функций непрерывен.

К дифференцируемости

Если $S$ интервал и все функции $f_{n}$ дифференцируемы и сходятся к пределу $f$, часто желательно определить производную функцию $f'$ взяв предел последовательности $f'_{n}$. Однако это, вообще говоря, невозможно: даже если сходимость равномерна, предельная функция не обязательно должна быть дифференцируемой (даже если последовательность состоит из всюду аналитических функций, см. функцию Вейерштрасса ), и даже если она дифференцируема, производная предельная функция не обязательно должна быть равна пределу производных. Рассмотрим, например $f_{n}(x)=n^{-1/2}{\sin(nx)}$ с единым лимитом $f_{n}\rightrightarrows f\equiv 0$. Четко, $f'$ также тождественно равен нулю. Однако производные последовательности функций имеют вид $f'_{n}(x)=n^{1/2}\cos nx,$ и последовательность $f'_{n}$ не сходится к $f',$ или даже к какой-либо функции вообще. Для того чтобы обеспечить связь предела последовательности дифференцируемых функций с пределом последовательности производных, необходима равномерная сходимость последовательности производных плюс сходимость последовательности функций хотя бы в одной точке:

Если $(f_{n})$ представляет собой последовательность дифференцируемых функций на $[a,b]$ такой, что $\lim _{n\to \infty }f_{n}(x_{0})$ существует (и конечно) для некоторого $x_{0}\in [a,b]$ и последовательность $(f'_{n})$ сходится равномерно на $[a,b]$, затем $f_{n}$ сходится равномерно к функции $f$ на $[a,b]$, и $f'(x)=\lim _{n\to \infty }f'_{n}(x)$ для $x\in [a,b]$.

К интегрируемости

Точно так же часто хочется поменять местами интегралы и ограничить процессы. Для интеграла Римана это можно сделать, если предположить равномерную сходимость:

Если $(f_{n})_{n=1}^{\infty }$ представляет собой последовательность функций, интегрируемых по Риману, определенных на компактном интервале $I$ которые равномерно сходятся с пределом $f$, затем $f$ интегрируема по Риману, и ее интеграл можно вычислить как предел интегралов $f_{n}$:

$$\int _{I}f=\lim _{n\to \infty }\int _{I}f_{n}.$$

Действительно, для равномерно сходящегося семейства ограниченных функций на интервале верхний и нижний интегралы Римана сходятся к верхнему и нижнему интегралам Римана предельной функции. Это следует из того, что при достаточно большом n график $f_{n}$ находится в пределах ε графика f , поэтому верхняя сумма и нижняя сумма $f_{n}$ каждый внутри $\varepsilon |I|$ значений верхней и нижней сумм $f$, соответственно.

Гораздо более сильные теоремы в этом отношении, требующие не более чем поточечной сходимости, можно получить, если отказаться от интеграла Римана и использовать вместо него интеграл Лебега .

К аналитичности

Используя теорему Мореры , можно показать, что если последовательность аналитических функций сходится равномерно в области S комплексной плоскости, то предел является аналитическим в S. Этот пример демонстрирует, что комплексные функции ведут себя более хорошо, чем действительные функции, поскольку равномерный предел аналитических функций на вещественном интервале даже не обязательно должен быть дифференцируемым (см. функцию Вейерштрасса ).

В серию

Мы говорим, что ${\textstyle \sum _{n=1}^{\infty }f_{n}}$ сходится:

1. поточечно на E тогда и только тогда, когда последовательность частичных сумм $s_{n}(x)=\sum _{j=1}^{n}f_{j}(x)$ сходится для каждого $x\in E$.
2. равномерно на E тогда и только тогда, когда s _n сходится равномерно при $n\to \infty$.
3. абсолютно на E тогда и только тогда, когда ${\textstyle \sum _{n=1}^{\infty }|f_{n}|}$ сходится для каждого $x\in E$.

Это определение дает следующий результат:

Пусть x0 _fn содержится в множестве и каждая непрерывна _точке в x0 _. E Если ${\textstyle f=\sum _{n=1}^{\infty }f_{n}}$ на E то f непрерывна в точке x0 _, в E. сходится равномерно Предположим, что $E=[a,b]$ и каждая f _n интегрируема на E . Если ${\textstyle \sum _{n=1}^{\infty }f_{n}}$ сходится равномерно на E , то f интегрируемо на E и ряд интегралов от равен _fn интегралу ряда от _fn .

Почти

Если областью определения функций является пространство с мерой E, связанное с этим понятие почти равномерной сходимости то можно определить . Мы говорим, что последовательность функций $(f_{n})$ сходится почти равномерно на E, если для любого $\delta >0$ существует измеримое множество $E_{\delta }$ с мерой меньше $\delta$ такая, что последовательность функций $(f_{n})$ сходится равномерно на $E\setminus E_{\delta }$. Другими словами, почти равномерная сходимость означает, что существуют множества сколь угодно малой меры, для которых последовательность функций сходится равномерно на своем дополнении.

Заметим, что почти равномерная сходимость последовательности не означает, что она сходится равномерно почти всюду, как следует из названия. Однако теорема Егорова гарантирует, что на конечном пространстве с мерой последовательность функций, сходящаяся почти всюду, также сходится почти равномерно на одном и том же множестве.

Почти равномерная сходимость предполагает сходимость почти всюду и сходимость по мере .

См. также

• Равномерная сходимость по вероятности
• Способы конвергенции (аннотированный указатель)
• Теорема Дини
• Теорема Арсела – Асколи

Ссылки

• Конрад Кнопп , Теория и применение бесконечных рядов ; Блэки и сын, Лондон, 1954 г., перепечатано Dover Publications, ISBN   0-486-66165-2 .
• Г.Х. Харди , сэр Джордж Стоукс и концепция равномерной конвергенции ; Proceedings of the Cambridge Philosophical Society , 19 , стр. 148–156 (1918).
• Бурбаки ; Элементы математики: Общая топология. Главы 5–10 (мягкая обложка) ; ISBN   0-387-19374-X
• Уолтер Рудин , Принципы математического анализа , 3-е изд., McGraw – Hill, 1976.
• Джеральд Фолланд , Реальный анализ: современные методы и их применение, второе издание, John Wiley & Sons, Inc., 1999, ISBN   0-471-31716-0 .
• Уильям Уэйд, Введение в анализ , 3-е изд., Pearson, 2005 г.

Внешние ссылки

• «Равномерная сходимость» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Графические примеры равномерной сходимости рядов Фурье от Университета Колорадо.