Тригонометрический ряд

Эта статья о математической концепции. Чтобы узнать о книге Зигмунда, см. «Тригонометрический ряд» .

В математике тригонометрический ряд — это бесконечный ряд вида

$A_{0}+\sum _{n=1}^{\infty }A_{n}\cos {nx}+B_{n}\sin {nx},$

где $x$ это переменная и $\{A_{n}\}$ и $\{B_{n}\}$являются коэффициентами . Это бесконечная версия тригонометрического полинома .

Тригонометрический ряд называется рядом Фурье интегрируемой функции ${\textstyle f}$ если коэффициенты имеют вид:

$A_{n}={\frac {1}{\pi }}\int _{0}^{2\pi }\!f(x)\cos {nx}\,dx$

$B_{n}={\frac {1}{\pi }}\displaystyle \int _{0}^{2\pi }\!f(x)\sin {nx}\,dx$

Примеры

Ряд Фурье для тождественной функции страдает от явления Гиббса вблизи концов периодического интервала.

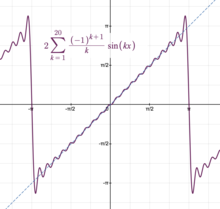
Любой ряд Фурье является примером тригонометрического ряда. Пусть функция $f(x)=x$ на $[-\pi ,\pi ]$периодически расширяться (см. пилообразную волну ). Тогда его коэффициенты Фурье будут:

${\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\cos {nx}\,dx=0,\quad n\geq 0.\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\sin {nx}\,dx\\[4pt]&=-{\frac {x}{n\pi }}\cos {nx}+{\frac {1}{n^{2}\pi }}\sin {nx}{\Bigg \vert }_{x=-\pi }^{\pi }\\[5mu]&={\frac {2\,(-1)^{n+1}}{n}},\quad n\geq 1.\end{aligned}}$

Что дает пример тригонометрического ряда:

$2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin {nx}=2\sin {x}-{\frac {2}{2}}\sin {2x}+{\frac {2}{3}}\sin {3x}-{\frac {2}{4}}\sin {4x}+\cdots$

Тригонометрический ряд sin 2 x /log 2 + sin 3 x /log 3 + sin 4 x /log 4 +... не является рядом Фурье.

Однако обратное неверно: не каждый тригонометрический ряд является рядом Фурье. Сериал

$\sum _{n=2}^{\infty }{\frac {\sin {nx}}{\log {n}}}={\frac {\sin {2x}}{\log {2}}}+{\frac {\sin {3x}}{\log {3}}}+{\frac {\sin {4x}}{\log {4}}}+\cdots$

тригонометрический ряд, сходящийся при всех $x$ но не является рядом Фурье . Здесь $B_{n}={\frac {1}{\log(n)}}$ для $n\geq 2$ а все остальные коэффициенты равны нулю.

тригонометрического

Уникальность и нули тригонометрических рядов были активной областью исследований в Европе XIX века. Во-первых, Георг Кантор доказал, что если тригонометрический ряд сходится к функции $f(x)$ на интервале $[0,2\pi ]$, который тождественно равен нулю или, в более общем смысле, отличен от нуля не более чем в конечном числе точек, то все коэффициенты ряда равны нулю.

Позднее Кантор доказал, что даже если множество S , на котором $f$ненулевое, бесконечное, но производное множество S' из S конечно, то все коэффициенты равны нулю. На самом деле он доказал более общий результат. Пусть S ₀ = S и пусть S _k+1 — производное множество S _k . Если существует конечное число n, которого Sn _для конечно, то все коэффициенты равны нулю. Позже Лебег доказал, что если существует счетный бесконечный ординал α такой, что S _α конечен, то все коэффициенты ряда равны нулю. Работа Кантора над проблемой уникальности, как известно, привела его к изобретению трансфинитных порядковых чисел , которые появились как индексы α в S _α .

Ссылки

• Бари, Нина Карловна (1964). Трактат о тригонометрических рядах . Том. 1. Перевод Маллинза, Маргарет Ф. Пергамон.
• Зигмунд, Антони (1968). Тригонометрический ряд . Том. 1 и 2 (2-е, переиздание). Издательство Кембриджского университета. МР   0236587 .

См. также

• Теорема Данжуа–Лузина