1 + 1 + 1 + 1 + ⋯

Ряд 1 + 1 + 1 + 1 + ⋯

После сглаживания

Асимптотика сглаживания. - пересечение Y линии — ⁠ 1 / 2 ⁠ .

В математике , 1 + 1 + 1 + 1 + ⋯ пишется также ⁠ $\textstyle \sum _{n=1}^{\infty }n^{0}$⁠ , ⁠ $\textstyle \sum _{n=1}^{\infty }1^{n}$⁠ или просто ⁠ $\textstyle \sum _{n=1}^{\infty }1$⁠ — расходящийся ряд . Тем не менее, иногда предполагается, что его стоимость равна ⁠. $-{\tfrac {1}{2}}$⁠ , особенно по физике. Это значение можно обосновать некоторыми математическими методами получения значений из расходящихся рядов, включая регуляризацию дзета-функции .

Как расходящийся сериал

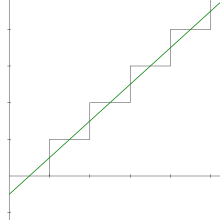
1 + 1 + 1 + 1 + ⋯ — расходящийся ряд, а это означает, что его последовательность частичных сумм не сходится к пределу в действительных числах .

Последовательность 1 ^н можно рассматривать как геометрический ряд с общим отношением 1. Для некоторых других расходящихся геометрических рядов, включая ряд Гранди с отношением −1 и ряд 1 + 2 + 4 + 8 + ⋯ с соотношением 2, можно использовать общий решение суммы геометрической прогрессии с основанием 1 и отношением ⁠ $r$⁠ , получение ⁠ ${\tfrac {1}{1-r}}$⁠ , но этот метод суммирования не работает для 1 + 1 + 1 + 1 + ⋯ , что приводит к делению на ноль .

Вместе с рядом Гранди это одна из двух геометрических серий с рациональным соотношением, расходящихся как для действительных чисел, так и для всех систем p -адических чисел .

В контексте расширенной линии действительных чисел

$\sum _{n=1}^{\infty }1=+\infty \,,$

поскольку его последовательность частичных сумм монотонно и неограниченно возрастает.

Регуляризация дзета-функции

Где сумма n ⁰ происходит в физических приложениях, иногда его можно интерпретировать с помощью регуляризации дзета-функции , как значение при s = 0 Римана дзета-функции :

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1-2^{1-s}}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}\,.$

Однако две приведенные выше формулы недействительны в нуле, но аналитическое продолжение имеет вид

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)$

Используя это, получаем (учитывая, что Γ(1) = 1 ),

$\zeta (0)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \sin \left({\frac {\pi s}{2}}\right)\ \zeta (1-s)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \left({\frac {\pi s}{2}}-{\frac {\pi ^{3}s^{3}}{48}}+...\right)\ \left(-{\frac {1}{s}}+...\right)=-{\frac {1}{2}}$

где разложение в степенной ряд для ζ ( s ) относительно s = 1 следует, потому что ζ ( s ) имеет там простой полюс вычета один. В этом смысле 1 + 1 + 1 + 1 + ⋯ = ζ (0) = − ⁠ 1 / 2 ⁠ .

Эмилио Элизальде представляет комментарий других об этой серии, предполагающий центральную роль регуляризации дзета-функции этого ряда в физике:

За короткий период, менее года, два выдающихся физика, А. Славнов и Ф. Индурайн , провели в Барселоне семинары по разным темам. Примечательно, что в обоих выступлениях в какой-то момент докладчик обратился к аудитории со словами: « Как всем известно , 1 + 1 + 1 + ⋯ = − ⁠ 1/2 ​ ⁠ . ' Подразумевая «может быть»: если вы этого не знаете, продолжать слушать бесполезно.

См. также

• сериал Гранди
• 1 − 2 + 3 − 4 + · · ·
• 1 + 2 + 3 + 4 + · · ·
• 1 + 2 + 4 + 8 + · · ·
• 1 − 2 + 4 − 8 + ⋯
• 1 − 1 + 2 − 6 + 24 − 120 + · · ·
• Гармоническая серия

Внешние ссылки

• Последовательность OEIS A000012 (Простейшая последовательность положительных чисел: последовательность всех единиц)