История тригонометрии
| Тригонометрия |
|---|
 |
| Ссылка |
| Законы и теоремы |
| Исчисление |
| Математики |
Раннее изучение треугольников можно отнести ко 2-му тысячелетию до нашей эры , в египетской математике ( Риндский математический папирус ) и вавилонской математике . Тригонометрия также была распространена в кушитской математике. [1] Систематическое изучение тригонометрических функций началось в эллинистической математике , достигнув Индии как часть эллинистической астрономии . [2] В индийской астрономии изучение тригонометрических функций процветало в период Гуптов , особенно благодаря Арьябхате (шестой век нашей эры), который открыл функции синуса, косинуса и версуса.
В средние века изучение тригонометрии продолжалось в исламской математике такими математиками, как Аль-Хорезми и Абу аль-Вафа . Она стала самостоятельной дисциплиной в исламском мире все шесть тригонометрических функций , где были известны . Переводы арабских и греческих текстов привели к тому, что тригонометрия была принята в качестве предмета на Латинском Западе, начиная с эпохи Возрождения с Региомонтаном .
Развитие современной тригонометрии изменилось в западную эпоху Просвещения , начиная с математики 17-го века ( Исаак Ньютон и Джеймс Стирлинг ) и достигая своей современной формы с Леонардом Эйлером (1748).
Этимология [ править ]
Термин «тригонометрия» произошел от греческого τρίγωνον trigōnon — «треугольник» и μέτρον Metron — «мера». [3]
Современные слова «синус» и «косинус» произошли от латинского слова sinus в результате неправильного перевода с арабского языка (см. Синус и косинус#Этимология ). В частности, Фибоначчи пазуха влияние на создание этого термина оказала прямая . [4]
Слово «тангенс» происходит от латинского tangens, означающего «касание», поскольку линия касается круга единичного радиуса, тогда как секанс происходит от латинского secans «разрез», поскольку линия пересекает круг. [5]
Префикс « co- » (в «косинусе», «котангенсе», «косекансе») встречается в Эдмунда Гюнтера » «Каноне треугольника (1620 г.), в котором косинус определяется как сокращение от sinus Complimenti (синус дополнительного угла). ) и аналогичным образом определяет котангены . [6] [7]
Слова «минута» и «секунда» произошли от латинских фраз partes minutae primae и partes minutae secundae . [8] Это примерно переводится как «первые мелкие детали» и «вторые мелкие детали».
Древний [ править ]
Древний Ближний Восток [ править ]
Древним египтянам и вавилонянам на протяжении многих столетий были известны теоремы о соотношениях сторон подобных треугольников. Однако, поскольку в доэллинских обществах не было понятия меры угла, вместо этого они ограничивались изучением сторон треугольников. [9]
Вавилонские астрономы вели подробные записи о восходе и заходе звезд , движении планет , солнечных и лунных затмениях , и все это требовало знания угловых расстояний, измеряемых на небесной сфере . [10] Основываясь на одной из интерпретаций таблички Плимптона 322 клинописной (ок. 1900 г. до н. э.), некоторые даже утверждали, что у древних вавилонян была таблица секущих, но она не работает в этом контексте, поскольку без использования кругов и углов в ситуации победили современные тригонометрические обозначения. Не применяю. [11] Однако существует много споров о том, является ли это таблицей троек Пифагора , решением квадратных уравнений или тригонометрической таблицей .
С другой стороны, египтяне использовали примитивную форму тригонометрии для строительства пирамид во 2-м тысячелетии до нашей эры. [10] , Математический папирус Ринда написанный египетским писцом Ахмесом (ок. 1680–1620 до н. э.), содержит следующую задачу, связанную с тригонометрией: [10]
«Если высота пирамиды 250 локтей, а длина стороны ее основания 360 локтей, чему равен ее секек ?»
Решение проблемы Ахмесом - это отношение половины стороны основания пирамиды к ее высоте, или отношение высоты к высоте ее грани. Другими словами, найденная им величина для секеда является котангенсом угла основания пирамиды и ее грани. [10]
Классическая античность [ править ]
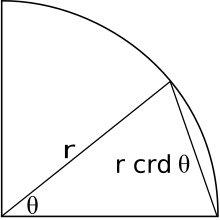
Древнегреческие и эллинистические математики использовали аккорд . Учитывая окружность и дугу на окружности, хорда — это линия, стягивающая дугу. Биссектриса хорды проходит через центр окружности и делит угол пополам. Половина биссектрисы представляет собой синус половины биссектрисы угла, то есть: [12]
и, следовательно, функция синуса также известна как полухорда . Благодаря этой взаимосвязи ряд тригонометрических тождеств и теорем, известных сегодня, были также известны эллинистическим математикам, но в их эквивалентной хордовой форме. [13] [14]
нет тригонометрии Хотя в трудах Евклида и Архимеда , в строгом смысле этого слова есть теоремы, изложенные геометрическим (а не тригонометрическим) способом, эквивалентные конкретным тригонометрическим законам или формулам. [9] Например, двенадцатое и тринадцатое положения второй книги «Начал » представляют собой законы косинусов для тупых и острых углов соответственно. Теоремы о длинах хорд являются приложениями закона синусов . А теорема Архимеда о разорванных хордах эквивалентна формулам синусов сумм и разностей углов. [9] Чтобы компенсировать отсутствие таблицы аккордов , математики времен Аристарха иногда использовали утверждение, что в современных обозначениях sin α /sin β < α / β < tan α /tan β всякий раз, когда 0 ° < β < α < 90°, ныне известное как неравенство Аристарха . [15]
Первая тригонометрическая таблица, по-видимому, была составлена Гиппархом Никейским . (180–125 гг. до н.э.), который теперь известен как «отец тригонометрии» [16] Гиппарх был первым, кто составил таблицу соответствующих значений дуги и хорды для ряда углов. [4] [16]
Хотя неизвестно, когда систематическое использование круга в 360° пришло в математику, известно, что систематическое введение круга в 360° произошло вскоре после того, как Аристарх Самосский сочинил «О размерах и расстояниях Солнца и Луны» (ок. 260 г. до н.э.), так как он измерял угол в долях квадранта. [15] Кажется, что систематическое использование круга в 360° во многом связано с Гиппархом и его таблицей аккордов . Гиппарх, возможно, позаимствовал идею этого деления у Гипсикла , который ранее разделил сутки на 360 частей, деление суток, возможно, было предложено вавилонской астрономией. [17] В древней астрономии зодиак был разделен на двенадцать «знаков» или тридцать шесть «деканов». Сезонный цикл продолжительностью примерно 360 дней мог бы соответствовать знакам и деканам зодиака, если разделить каждый знак на тридцать частей, а каждый декан — на десять частей. [8] Благодаря вавилонской шестидесятеричной системе счисления каждая степень делится на шестьдесят минут, а каждая минута — на шестьдесят секунд. [8]
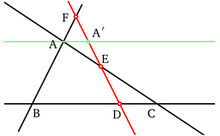
Менелай Александрийский (ок. 100 г. н. э.) написал в трёх книгах свою «Сферику» . В книге I он установил основу сферических треугольников, аналогичную евклидовой основе плоских треугольников. [14] Он установил теорему, не имеющую евклидова аналога, о том, что два сферических треугольника равны, если соответствующие углы равны, но он не различал равные и симметричные сферические треугольники. [14] Другая теорема, которую он установил, заключается в том, что сумма углов сферического треугольника больше 180 °. [14] Книга II «Сферики» применяет сферическую геометрию к астрономии. А в третьей книге содержится «теорема Менелая». [14] Далее он дал свое знаменитое «правило шести величин». [18]
Позже Клавдий Птолемей (ок. 90 – ок. 168 г. н. э.) расширил тему «Акорды в круге » Гиппарха в своем «Альмагесте» , или « Математическом синтаксисе» . «Альмагест» — это прежде всего работа по астрономии, а астрономия опирается на тригонометрию. Таблица хорд Птолемея дает длины хорд круга диаметром 120 в зависимости от количества градусов n в соответствующей дуге круга для n в диапазоне от 1/2 до 180 с шагом 1/2. [19] Тринадцать книг Альмагеста — самый влиятельный и значительный тригонометрический труд всей древности. [20] Теорема, которая была центральной в вычислении хорд Птолемеем, была тем, что до сих пор известно как теорема Птолемея , о том, что сумма произведений противоположных сторон вписанного четырехугольника равна произведению диагоналей. Частный случай теоремы Птолемея появился как предложение 93 в «Данных» Евклида . Теорема Птолемея приводит к эквиваленту четырех формул суммы и разности для синуса и косинуса, которые сегодня известны как формулы Птолемея, хотя сам Птолемей использовал хорды вместо синуса и косинуса. [20] Птолемей далее вывел эквивалент формулы половинного угла.
Птолемей использовал эти результаты для создания своих тригонометрических таблиц, но невозможно определить, были ли эти таблицы получены на основе работы Гиппарха. [20]
Ни таблицы Гиппарха, ни таблицы Птолемея до наших дней не сохранились, хотя описания других античных авторов не оставляют сомнений в их существовании. [21]
Индийская математика [ править ]
Некоторые из первых и очень значительных разработок тригонометрии произошли в Индии . Влиятельные произведения IV–V веков нашей эры, известные как Сиддханты (их было пять, наиболее важным из которых является Сурья Сиддханта). [22] ) первым определил синус как современное соотношение между половиной угла и половиной хорды, а также определил косинус, версус и обратный синус . [23] Вскоре после этого другой индийский математик и астроном , Арьябхата (476–550 гг. н.э.), собрал и расширил разработки сиддхантов в важной работе под названием « Арьябхатия» . [24] Сиддханты (1 - косинус) с интервалами 3,75 ° от 0 ° до и Арьябхатия содержат самые ранние из сохранившихся таблиц значений синуса и версинуса 90 ° с точностью до 4 десятичных знаков. [25] Они использовали слова джья для синуса, коджья для косинуса, уткрама-джья для версины и открам джья для обратного синуса. Слова jya и kojya в конечном итоге стали синусом и косинусом соответственно после неправильного перевода, описанного выше.
В VII веке Бхаскара I вывел формулу для вычисления синуса острого угла без использования таблицы. Он также дал следующую аппроксимирующую формулу для sin( x ), относительная погрешность которой составляла менее 1,9%:
Позже, в VII веке, Брахмагупта переработал формулу.
(также полученная ранее, как упоминалось выше) и интерполяционная формула Брахмагупты для вычисления значений синуса. [11]
Другим более поздним индийским автором тригонометрии был Бхаскара II, живший в XII веке. Бхаскара II разработал сферическую тригонометрию и обнаружил множество тригонометрических результатов.
Бхаскара II был одним из первых, кто открыл и тригонометрические результаты, такие как:
Мадхава (около 1400 г.) добился первых успехов в анализе тригонометрических функций и их разложении в бесконечные ряды . Он разработал концепции степенного ряда и ряда Тейлора , а также разложил степенные ряды синуса, косинуса, тангенса и арктангенса. [26] [27] Используя аппроксимации синуса и косинуса рядами Тейлора, он создал таблицу синусов с точностью до 12 десятичных знаков и таблицу косинусов с точностью до 9 десятичных знаков. Он также дал степенной ряд π и угла , радиуса , диаметра и длины окружности через тригонометрические функции. Его работы были расширены его последователями в школе Кералы до 16 века. [26] [27]
| Нет. | Ряд | Имя | Западные первооткрыватели сериала и примерные даты открытия [28] |
|---|---|---|---|
| 1 | грех х = х - х 3 / 3! + х 5 / 5! − х 7 / 7! + ... | Синусоидальный ряд Мадхавы | Исаак Ньютон (1670 г.) и Вильгельм Лейбниц (1676 г.) |
| 2 | потому что х = 1 - х 2 / 2! + х 4 / 4! − х 6 / 6! + ... | Косинусный ряд Мадхавы | Исаак Ньютон (1670 г.) и Вильгельм Лейбниц (1676 г.) |
| 3 | загар −1 х = х - х 3 / 3 + х 5 / 5 − х 7 / 7 + ... | Арктангенсный ряд Мадхавы | Джеймс Грегори (1671 г.) и Вильгельм Лейбниц (1676 г.) |
Индийский текст Юктибхаша содержит доказательство расширения функций синуса и косинуса , а также вывод и доказательство степенного ряда для обратного тангенса , открытого Мадхавой. Юктибхаша также содержит правила нахождения синусов и косинусов суммы и разности двух углов.
Китайская математика [ править ]

В Китае математическую китайскую таблица синусов Арьябхаты была переведена в книгу Кайюань Чжаньцзин , составленную в 718 году нашей эры во времена династии Тан . [29] Хотя китайцы преуспели в других областях математики, таких как твердотельная геометрия, биномиальная теорема и сложные алгебраические формулы, ранние формы тригонометрии не получили такого широкого признания, как в более ранних греческих, эллинистических, индийских и исламских мирах. [30] Вместо этого ранние китайцы использовали эмпирическую замену, известную как чунг ча , в то время как практическое использование плоской тригонометрии для использования синуса, тангенса и секанса было известно. [29] Однако это зачаточное состояние тригонометрии в Китае начало медленно меняться и развиваться во время династии Сун (960–1279), когда китайские математики начали уделять больше внимания необходимости сферической тригонометрии в календарной науке и астрономических расчетах. [29] Китайский ученый- эрудит , математик и чиновник Шэнь Го (1031–1095) использовал тригонометрические функции для решения математических задач о хордах и дугах. [29] Виктор Дж. Кац пишет, что в формуле Шена «техника пересекающихся кругов» он создал аппроксимацию дуг s круга, учитывая диаметр d , сагитту v и длину c хорды, стягивающей дугу, длину которой он аппроксимируется как [31]
Сал Рестиво пишет, что работы Шена по длинам дуг окружностей легли в основу сферической тригонометрии, разработанной в 13 веке математиком и астрономом Го Шоуцзином (1231–1316). [32] Как утверждают историки Л. Гоше и Джозеф Нидэм, Го Шоуцзин использовал сферическую тригонометрию в своих расчетах для совершенствования календарной системы и китайской астрономии . [29] [33] Наряду с китайской иллюстрацией математических доказательств Го, датированной более поздним XVII веком, Нидхэм утверждает, что:
Го использовал четырехугольную сферическую пирамиду, базальный четырехугольник которой состоял из одной экваториальной и одной эклиптической дуги вместе с двумя дугами меридиана , одна из которых проходила через точку летнего солнцестояния ... Такими методами он смог получить ду люй. (градусы экватора, соответствующие градусам эклиптики), джи ча (значения хорд для заданных дуг эклиптики) и ча лю (разница между хордами дуг, отличающихся на 1 градус). [34]
Несмотря на достижения работ Шэня и Го в области тригонометрии, еще одна существенная работа по китайской тригонометрии не будет опубликована снова до 1607 года, когда «Начала Евклида» были опубликованы одновременно китайским чиновником и астрономом Сюй Гуанци (1562–1633) и итальянским иезуитом Маттео Риччи. (1552–1610). [35]
исламский Средневековый мир

Предыдущие работы были позже переведены и расширены в средневековом исламском мире преимущественно мусульманскими математиками персидского и арабского происхождения , которые сформулировали большое количество теорем, которые освободили предмет тригонометрии от зависимости от полного четырехугольника , как это было в эллинистической математике благодаря к применению теоремы Менелая . По мнению Э.С. Кеннеди, именно после такого развития исламской математики «появилась первая настоящая тригонометрия, в том смысле, что только тогда объектом изучения стал сферический или плоский треугольник , его стороны и углы ». [36]
Были также известны методы работы со сферическими треугольниками, в частности метод Менелая Александрийского , который разработал «теорему Менелая» для решения сферических задач. [14] [37] Однако Э.С. Кеннеди отмечает, что, хотя в доисламской математике было возможно вычислить величины сферической фигуры, в принципе, с помощью таблицы хорд и теоремы Менелая, применение этой теоремы к сферическим задачам было очень трудным. сложно на практике. [38] Чтобы соблюдать святые дни по исламскому календарю, в котором время определялось фазами луны , астрономы сначала использовали метод Менелая для расчета места луны и звезд , хотя этот метод оказался неуклюжим и трудным. Это включало в себя создание двух пересекающихся прямоугольных треугольников ; применив теорему Менелая, можно было решить одну из шести сторон, но только если были известны остальные пять сторон. Например, чтобы определить время по , Солнца высоте требовалось неоднократное применение теоремы Менелая. Перед средневековыми исламскими астрономами стояла очевидная задача найти более простой тригонометрический метод. [39]
В начале 9 века нашей эры Мухаммад ибн Муса аль-Хорезми создал точные таблицы синусов и косинусов, а также первую таблицу тангенсов. Он также был пионером сферической тригонометрии . В 830 году нашей эры Хабаш аль-Хасиб аль-Марвази составил первую таблицу котангенсов. [40] [41] Мухаммад ибн Джабир аль-Харрани аль-Баттани (Албатениус) (853–929 гг. н. э.) открыл взаимные функции секущего и косеканса и составил первую таблицу косекансов для каждой степени от 1 ° до 90 °. [42]
К 10 веку нашей эры в работах Абу аль-Вафа аль-Бузджани все шесть тригонометрических функций . использовались [43] У Абу аль-Вафа были таблицы синусов с шагом 0,25 °, с точностью до 8 десятичных знаков, а также точные таблицы значений тангенсов. [43] Он также разработал следующую тригонометрическую формулу: [44]
- (частный случай формулы сложения углов Птолемея; см. выше)
В своем оригинальном тексте Абу аль-Вафа утверждает: «Если мы хотим этого, мы умножим данный синус на косинус минут , и результат будет половиной синуса двойного числа». [44] Абу аль-Вафа также установил тождества сложения и разности углов, представленные с полными доказательствами: [44]
Для второго в тексте говорится: «Мы умножаем синус каждой из двух дуг на косинус остальных минут . Если нам нужен синус суммы, мы складываем произведения, если мы хотим синус разности , мы берем их разницу». [44]
Он также открыл закон синусов для сферической тригонометрии: [40]
Также в конце 10-го и начале 11-го веков нашей эры египетский астроном Ибн Юнус выполнил множество тщательных тригонометрических расчетов и продемонстрировал следующее тригонометрическое тождество : [45]
Аль-Джайани (989–1079) из Аль-Андалуса написал «Книгу неизвестных дуг сферы », которую считают «первым трактатом по сферической тригонометрии ». [46] Он «содержит формулы для правосторонних треугольников , общий закон синусов и решение сферического треугольника с помощью полярного треугольника». Позже этот трактат оказал «сильное влияние на европейскую математику», а его «определение отношений как чисел» и «метод решения сферического треугольника, когда все стороны неизвестны», вероятно, повлияли на Региомонтануса . [46]
Метод триангуляции был впервые разработан мусульманскими математиками, которые применили его для практических целей, таких как геодезия. [47] и исламская география , описанная Абу Райханом Бируни в начале 11 века. Сам Бируни представил методы триангуляции для измерения размеров Земли и расстояний между различными местами. [48] В конце XI века Омар Хайям (1048–1131) решал кубические уравнения , используя приближенные численные решения, найденные путем интерполяции в тригонометрических таблицах. В 13 веке Насир ад-Дин ат-Туси был первым, кто рассматривал тригонометрию как математическую дисциплину, независимую от астрономии, и развил сферическую тригонометрию в ее нынешнюю форму. [41] Он перечислил шесть различных случаев прямоугольного треугольника в сферической тригонометрии, а в своей работе «О фигуре сектора » он сформулировал закон синусов для плоских и сферических треугольников, открыл закон тангенсов для сферических треугольников и представил доказательства обоих. эти законы. [49] Насир ад-Дин ат-Туси считается создателем тригонометрии как самостоятельной математической дисциплины. [50] [51] [52]
В 15 веке Джамшид аль-Каши предоставил первое явное изложение закона косинусов в форме, подходящей для триангуляции . [ нужна ссылка ] Во Франции закон косинусов до сих пор называют теоремой Аль-Каши . Он также дал тригонометрические таблицы значений функции синуса для четырех шестидесятеричных цифр (что эквивалентно 8 десятичным знакам) для каждого 1 градуса аргумента с разностями, которые необходимо прибавлять для каждой 1/60 1 градуса. [ нужна ссылка ] Примерно в то же время Улугбек также дает точные таблицы синусов и тангенсов с точностью до 8 знаков после запятой. [ нужна ссылка ]
Современный [ править ]
Этот раздел нуждается в расширении . Вы можете помочь, добавив к нему . ( март 2024 г. ) |
Европейский ренессанс и после него [ править ]
В 1342 году Леви бен Гершон, известный как Герсонид , написал «О синусах, хордах и дугах» , в частности доказав закон синуса для плоских треугольников и дав пятизначные таблицы синусов . [53]
Упрощенная тригонометрическая таблица « toleta de marteloio » использовалась моряками в Средиземном море в XIV-XV веках для расчета навигационных курсов. Он описан Рамоном Луллием Майорки венецианского в 1295 году и изложен в атласе 1436 года капитана Андреа Бьянко .
Региомонтан был, пожалуй, первым математиком в Европе, который рассматривал тригонометрию как отдельную математическую дисциплину. [54] в его De triangulis omnimodis, написанном в 1464 году, а также в его более поздней Tabulae Directionum , которая включала безымянную функцию тангенса.Opus palatinum de triangulis Георга Иоахима Ретикуса , ученика Коперника , был, вероятно, первым в Европе, который определил тригонометрические функции непосредственно в терминах прямоугольных треугольников вместо кругов, с таблицами для всех шести тригонометрических функций; эта работа была завершена учеником Ретикуса Валентином Отоном в 1596 году.
В 17 веке Исаак Ньютон и Джеймс Стирлинг разработали общую интерполяционную формулу Ньютона – Стирлинга для тригонометрических функций.
В XVIII веке Леонарда Эйлера ( «Введение в анализ бесконечного анализа» 1748 г.) в основном положило начало аналитической трактовке тригонометрических функций в Европе, вывело их бесконечные ряды и представило « формулу Эйлера » . ix знак равно потому что Икс + я грех Икс . Эйлер использовал почти современные сокращения греха. , потому что. , Тан. , детская кроватка. , сек. , и косек. До этого Роджер Коутс вычислил производную синуса в своей «Harmonia Mensurarum» (1722). [55] Также в 18 веке Брук Тейлор определил общий ряд Тейлора и дал его разложение и приближения для всех шести тригонометрических функций. Работы Джеймса Грегори в 17 веке и Колена Маклорена в 18 веке также оказали большое влияние на развитие тригонометрических рядов.
См. также [ править ]
- Греческая математика
- История математики
- Тригонометрические функции
- Тригонометрия
- Таблица аккордов Птолемея
- Таблица синусов Арьябхаты
- Рациональная тригонометрия
Цитаты и сноски [ править ]
- ^ Отто Нойгебауэр (1975). История древней математической астрономии. 1 . Издательство Спрингер. п. 744. ИСБН 978-3-540-06995-9 .
- ^ Кац 1998 , с. 212.
- ^ «тригонометрия» . Интернет-словарь этимологии .
- ^ Jump up to: Перейти обратно: а б О'Коннор, Джей-Джей; Робертсон, Э.Ф. (1996). «Тригонометрические функции» . MacTutor Архив истории математики . Архивировано из оригинала 4 июня 2007 г.
- ^ Оксфордский словарь английского языка
- ^ Гюнтер, Эдмунд (1620). Канон треугольников
- ^ Рогель, Денис, изд. (6 декабря 2010 г.). «Реконструкция Треугольного канона Гюнтера (1620 г.)» (отчет об исследовании). ХЭЛ. инрия-00543938. Архивировано из оригинала 28 июля 2017 года . Проверено 28 июля 2017 г.
- ^ Jump up to: Перейти обратно: а б с Boyer 1991 , стр. 166–167 , Греческая тригонометрия и измерение: «Следует напомнить, что со времен Гиппарха до наших дней не существовало таких вещей, как тригонометрические отношения . Греки, а после них индусы и арабы использовали тригонометрические линии сначала приняли форму, как мы видели, хорд в круге, и Птолемею пришлось связать числовые значения (или приближения) с хордами [...] Вполне вероятно, что 260-градусная мера была перенесена из астрономии, где зодиак был разделен на двенадцать «знаков» или 36 «деканов». Цикл времен года продолжительностью примерно 360 дней можно было легко привести в соответствие с системой зодиакальных знаков и деканов. путем разделения каждого знака на тридцать частей и каждого декана на десять частей. Наша общая система измерения углов может возникнуть из этого соответствия. для Птолемея было естественным разделить свои степени на шестьдесят partes minutae primae , каждая из последних на шестьдесят partes minutae secundae и так далее. Именно от латинских словосочетаний, которые употребляли в связи с этим переводчики, произошли наши слова «минута» и «секунда». Несомненно, именно шестидесятеричная система побудила Птолемея разделить диаметр своего тригонометрического круга на 120 частей; каждую из них он далее разделил на шестьдесят минут и каждую минуту продолжительностью в шестьдесят секунд».
- ^ Jump up to: Перейти обратно: а б с Бойер 1991 , стр. 158–159 , Греческая тригонометрия и измерение: «Тригонометрия, как и другие разделы математики, не была работой какого-либо одного человека или нации. Теоремы об отношениях сторон подобных треугольников были известны, и использовался древними египтянами и вавилонянами. Ввиду отсутствия в доэллинскую эпоху концепции меры угла такое исследование лучше было бы назвать «трилатерометрией» или мерой трехсторонних многоугольников (трехсторонников), чем «тригонометрией». , мера частей треугольника. У греков мы впервые находим систематическое изучение отношений между углами (или дугами) в круге и длинами стягивающих их хорд. Свойства хорд как мер центральных и вписанных углов в кругах. , были знакомы грекам во времена Гиппократа, и вполне вероятно, что Евдокс использовал пропорции и угловые меры при определении размера Земли и относительных расстояний до Солнца и Луны. В трудах Евклида нет тригонометрии. в строгом смысле слова, но существуют теоремы, эквивалентные конкретным тригонометрическим законам или формулам. Предложения II.12 и 13 Элементы , например, представляют собой законы косинусов для тупых и острых углов соответственно, изложенные на геометрическом, а не тригонометрическом языке и доказанные методом, аналогичным тому, который использовал Евклид в связи с теоремой Пифагора. Теоремы о длинах хорд по сути являются применением современного закона синусов. Мы видели, что теорема Архимеда о разорванной хорде легко переводится на тригонометрический язык, аналогичный формулам для синусов сумм и разностей углов».
- ^ Jump up to: Перейти обратно: а б с д Маор, Эли (1998). Тригонометрические наслаждения . Издательство Принстонского университета . п. 20 . ISBN 978-0-691-09541-7 .
- ^ Jump up to: Перейти обратно: а б Джозеф 2000 , стр. 383–384.
- ^ Кац 1998 , с. 143.
- ^ Поскольку в этих исторических расчетах не использовался единичный круг, в формуле была необходима длина радиуса. Сравните это с современным использованием функции crd , которая предполагает в своем определении единичный круг.
- ^ Jump up to: Перейти обратно: а б с д и ж Бойер 1991 , с. 163 , Греческая тригонометрия и измерение: «В книге I этого трактата Менелай устанавливает основу для сферических треугольников, аналогичную основанию Евклида I для плоских треугольников. Включена теорема, не имеющая евклидова аналога, - что два сферических треугольника конгруэнтны, если соответствующие углы равны. (Менелай не различал конгруэнтные и симметричные сферические треугольники); и теорема А + В + С установлена > 180°. Вторая книга « Сферики» описывает применение сферической геометрии к астрономическим явлениям и не представляет большого математического интереса. III, последняя, содержит хорошо известную «теорему Менелая» как часть того, что по сути является сферической тригонометрией в типичной греческой форме – геометрией или тригонометрией хорд в круге. В кружке на рис. 10.4 мы должны написать эту хорду. AB — это двойной синус половины центрального угла AOB (умноженный на радиус круга). Менелай и его греческие преемники вместо этого называли AB просто хордой, соответствующей дуге AB. Если BOB’ — диаметр круга, то хорда A’ равна удвоенному косинусу половины угла AOB (умноженному на радиус круга)».
- ^ Jump up to: Перейти обратно: а б Бойер 1991 , с. 159 , Греческая тригонометрия и измерения: «Вместо этого у нас есть трактат, возможно, написанный раньше (ок. 260 г. до н.э.), « О размерах и расстояниях Солнца и Луны » , который предполагает геоцентрическую Вселенную. В этой работе Аристарх сделал наблюдение, что когда Луна наполовину полная, угол между лучами зрения на Солнце и Луну меньше прямого угла на одну тридцатую квадранта (Систематическое введение круга в 360° произошло несколько позже. В тригонометрии. На современном языке это означало бы, что отношение расстояний Луны к расстоянию Солнца (отношение ME к SE на рис. 10.1) равно sin(3°), поскольку тригонометрические таблицы еще не были разработаны, и Аристарх обратился к ним. известная геометрическая теорема того времени, которая теперь была бы выражена в неравенствах sin α/ sin β < α/β < tan α/ tan β, для 0° < β < α < 90°.)»
- ^ Jump up to: Перейти обратно: а б Бойер 1991 , с. 162 , Греческая тригонометрия и измерение: «На протяжении примерно двух с половиной столетий, от Гиппократа до Эратосфена, греческие математики изучали отношения между линиями и окружностями и применяли их в различных астрономических задачах, но систематической тригонометрии не получилось. Затем, предположительно во второй половине II века до н. э. первую тригонометрическую таблицу, по-видимому, составил астроном Гиппарх Никейский (ок. 180–ок. 125 до н. э.), заслуживший таким образом право называться «отцом тригонометрии». Аристарх знал, что в данном круге отношение дуги к хорде уменьшается по мере уменьшения дуги от 180 ° до 0 °, стремясь к пределу, равному 1. Однако оказывается, что только после того, как Гиппарх приступил к этой задаче, кто-либо составил таблицу соответствующих значений. дуги и хорды для целого ряда углов».
- ^ Бойер 1991 , с. 162 , Греческая тригонометрия и измерение: «Неизвестно, когда именно систематическое использование круга в 360° вошло в математику, но, по-видимому, это произошло во многом благодаря Гиппарху в связи с его таблицей хорд. Вполне возможно, что он взял на себя это дело. от Гипсикла, который ранее разделил день на части, такое деление, возможно, было предложено вавилонской астрономией».
- ^ Нидхэм 1986 , с. 108.
- ^ Тумер, Джеральд Дж. (1998). Альмагест Птолемея . Издательство Принстонского университета. ISBN 978-0-691-00260-6 .
- ^ Jump up to: Перейти обратно: а б с д Бойер 1991 , стр. 164–166 , Греческая тригонометрия и измерение: «Теорема Менелая сыграла фундаментальную роль в сферической тригонометрии и астрономии, но, безусловно, самая влиятельная и значимая тригонометрическая работа всей древности была написана Птолемеем Александрийским примерно наполовину. спустя столетие после Менелая. [...] О жизни автора мы знаем так же мало, как и о жизни автора «Элементов». Мы не знаем, когда и где родились Евклид и Птолемей. проводил наблюдения в Александрии со 127 по 151 год нашей эры и, следовательно, предположим, что он родился в конце I века. Суидас, писатель, живший в X веке, сообщил, что Птолемей жил при Марке Аврелии (императоре из нашей эры). 161–180).
Птолемея Предполагается, что «Альмагест» во многом обязан своими методами «Аккордам в круге Гиппарха», но степень этого долга невозможно достоверно оценить. Ясно, что в астрономии Птолемей использовал каталог положений звезд, завещанный Гиппархом, но невозможно определить, были ли тригонометрические таблицы Птолемея в значительной степени заимствованы из его выдающегося предшественника. [...] Центральным элементом расчета хорд Птолемея было геометрическое утверждение, до сих пор известное как «теорема Птолемея»: [...] то есть сумма произведений противоположных сторон вписанного четырехугольника равна произведению диагоналей. [...] Частный случай теоремы Птолемея появился в « Данных Евклида» (предложение 93): [...] Теорема Птолемея, следовательно, приводит к результату sin ( α - β ) = sin α cos β - cos α sin Б. Подобные рассуждения приводят к формуле [...] Эти четыре формулы суммы и разности, следовательно, сегодня часто известны как формулы Птолемея.
Именно формулу синуса разности – или, точнее, хорды разности – Птолемей нашел особенно полезной при построении своих таблиц. Другая формула, которая ему эффективно послужила, была эквивалентом нашей формулы половинного угла». - ^ Бойер 1991 , стр. 158–168.
- ^ Бойер 1991 , с. 208.
- ^ Бойер 1991 , с. 209.
- ^ Бойер 1991 , с. 210.
- ^ Бойер 1991 , с. 215.
- ^ Jump up to: Перейти обратно: а б О'Коннор, Джей-Джей; Робертсон, Э.Ф. (2000). «Мадхава Сангамаграммы» . MacTutor Архив истории математики .
- ^ Jump up to: Перейти обратно: а б Пирс, Ян Г. (2002). «Мадхава Сангамаграммы» . MacTutor Архив истории математики .
- ^ Чарльз Генри Эдвардс (1994). Историческое развитие исчисления . Серия Springer Study Edition (3-е изд.). Спрингер. п. 205. ИСБН 978-0-387-94313-8 .
- ^ Jump up to: Перейти обратно: а б с д и Нидэм 1986 , с. 109.
- ^ Нидхэм 1986 , стр. 108–109.
- ^ Кац 2007 , с. 308.
- ^ Рестиво 1992 , с. 32.
- ^ Гоше, Л. (1917). Заметки Коуо Чеу-Кинга о сферической тригонометрии . п. 151.
- ^ Нидхэм 1986 , стр. 109–110.
- ^ Нидхэм 1986 , с. 110.
- ^ Кеннеди, ES (1969). «История тригонометрии». 31-й ежегодник . Вашингтон, округ Колумбия: Национальный совет учителей математики. ( см. Хак, Сайед Номанул (1996). «Индийское и персидское происхождение». В Сейеде Хоссейне Насре ; Оливер Лиман (ред.). История исламской философии . Рутледж . стр. 52–70 [60–63]. ISBN 978-0-415-13159-9 . )
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Менелай Александрийский» , Архив истории математики MacTutor , Университет Сент-Эндрюса «Книга 3 посвящена сферической тригонометрии и включает теорему Менелая».
- ^ Кеннеди, ES (1969). «История тригонометрии». 31-й ежегодник . Вашингтон, округ Колумбия: Национальный совет учителей математики: 337. ( ср. Хак, Сайед Номанул (1996). «Индийское и персидское происхождение». В Сейеде Хоссейне Насре ; Оливер Лиман (ред.). История исламской философии . Рутледж . С. 52–70 [68]. ISBN 978-0-415-13159-9 . )
- ^ Джинджерич, Оуэн (апрель 1986 г.). «Исламская астрономия» . Научный американец . 254 (10): 74. Бибкод : 1986SciAm.254d..74G . doi : 10.1038/scientificamerican0486-74 . Архивировано из оригинала 1 января 2011 г. Проверено 18 мая 2008 г.
- ^ Jump up to: Перейти обратно: а б Жак Сезиано, «Исламская математика», с. 157, в Селин, Хелейн ; Д'Амброзио, Убиратан , ред. (2000). Математика в разных культурах: история незападной математики . Springer Science+Business Media . ISBN 978-1-4020-0260-1 .
- ^ Jump up to: Перейти обратно: а б «тригонометрия» . Британская энциклопедия . Проверено 21 июля 2008 г.
- ^ Маор, Эли (1998). Тригонометрические наслаждения . Принстон: Издательство Принстонского университета. п. 38. ISBN 978-0-691-15820-4 .
- ^ Jump up to: Перейти обратно: а б Бойер 1991 , с. 238.
- ^ Jump up to: Перейти обратно: а б с д Мусса, Али (2011). «Математические методы в Альмагесте Абу аль-Вафа и определениях Киблы». Арабские науки и философия . 21 (1). Издательство Кембриджского университета : 1–56. дои : 10.1017/S095742391000007X . S2CID 171015175 .
- ^ Уильям Чарльз Брайс, « Исторический атлас ислама », стр.413.
- ^ Jump up to: Перейти обратно: а б О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Абу Абдаллах Мухаммад ибн Муаз Аль-Джайани» , Архив истории математики MacTutor , Университет Сент-Эндрюс
- ^ Дональд Рутледж Хилл (1996), «Инженерное дело», в Рошди Рашид, Энциклопедия истории арабской науки , Vol. 3, с. 751–795 [769].
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Абу Аррайхан Мухаммад ибн Ахмад аль-Бируни» , Архив истории математики MacTutor , Университет Сент-Эндрюс
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Издательство Принстонского университета. п. 518. ИСБН 978-0-691-11485-9 .
- ^ «Биография Аль-Туси_Насира» . www-history.mcs.st-andrews.ac.uk . Проверено 5 августа 2018 г.
Одним из наиболее важных математических вкладов ат-Туси было создание тригонометрии как самостоятельной математической дисциплины, а не просто инструмента для астрономических приложений. В «Трактате о четырехугольнике» ат-Туси дал первое дошедшее до нас изложение всей системы плоской и сферической тригонометрии. Эта работа действительно является первой в истории по тригонометрии как самостоятельной отрасли чистой математики и первой, в которой изложены все шесть случаев прямоугольного сферического треугольника.
- ^ Берггрен, Дж. Л. (октябрь 2013 г.). «Исламская математика» . Кембриджская история науки . Издательство Кембриджского университета. стр. 62–83. дои : 10.1017/CHO9780511974007.004 . ISBN 978-0-511-97400-7 .
- ^ electricpulp.com. «ṬUSI, НАЦИР-АД-ДИН i. Биография - Иранская энциклопедия» . www.iranicaonline.org . Проверено 5 августа 2018 г.
Говорят, что его главный вклад в математику (Наср, 1996, стр. 208-214) принадлежит тригонометрии, которая впервые была составлена им как отдельная новая дисциплина. Его усилиям также обязана своим развитием сферическая тригонометрия, в том числе концепция шести основных формул решения сферических прямоугольных треугольников.
- ^ Чарльз Г. Симонсон (зима 2000 г.). «Математика Леви бен Гершона, Ралбага» (PDF) . Бехол Дерахеха Даеху . 10 . Издательство Университета Бар-Илан: 5–21.
- ^ Бойер 1991 , с. 274.
- ^ Кац, Виктор Дж. (ноябрь 1987 г.). «Исчисление тригонометрических функций» . История Математики . 14 (4): 311–324. дои : 10.1016/0315-0860(87)90064-4 . . Доказательство Котеса упомянуто на стр. 315.
Ссылки [ править ]
- Бойер, Карл Бенджамин (1991). История математики (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 978-0-471-54397-8 .
- Джозеф, Джордж Г. (2000). Герб павлина: неевропейские корни математики (2-е изд.). Лондон: Книги Пингвинов . ISBN 978-0-691-00659-8 .
- Кац, Виктор Дж. (1998). История математики / Введение (2-е изд.). Эддисон Уэсли. ISBN 978-0-321-01618-8 .
- Кац, Виктор Дж. (2007). Математика Египта, Месопотамии, Китая, Индии и ислама: справочник . Принстон: Издательство Принстонского университета. ISBN 978-0-691-11485-9 .
- Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о небе и Земле . Тайбэй: Caves Books, Ltd.
- Рестиво, Сал (1992). Математика в обществе и истории: социологические исследования . Дордрехт: Kluwer Academic Publishers. ISBN 1-4020-0039-1 .
Дальнейшее чтение [ править ]
- Браунмюль, Антон фон (1900–1903). тригонометрии ( Лекции по истории на немецком языке). Б. Г. Тойбнер.
- Кеннеди, Эдвард С. (1969). «История тригонометрии» . Исторические темы для урока математики . Ежегодники NCTM. Том. 31. Национальный совет учителей математики. стр. 333–375.
- Маор, Эли (1998). Тригонометрические наслаждения . Издательство Принстонского университета. дои : 10.1515/9780691202204 . ISBN 0691057540 . Архивировано из оригинала 11 июля 2003 г.
- Остерманн, Александр; Ваннер, Герхард (2012). «Тригонометрия». Геометрия в ее истории . Тексты для бакалавриата по математике. Спрингер. стр. 113–155. дои : 10.1007/978-3-642-29163-0 . ISBN 978-3-642-29162-3 .
- Ван Браммелен, Глен (2009). Математика неба и земли: ранняя история тригонометрии . Издательство Принстонского университета.
- Ван Браммелен, Глен (2021). Учение о треугольниках: история современной тригонометрии . Издательство Принстонского университета.














