Джеймс Грегори (математик)

Джеймс Грегори
Джеймс Грегори (1638–1675)
Рожденный	Ноябрь 1638 г. ( 1638-11 ) Друмок , Абердиншир , Шотландия
Умер	октябрь 1675 г. ) ( 1675-10-00 ) ( 36 лет Эдинбург , Шотландия
Национальность	шотландский
Гражданство	Шотландия
Альма-матер	Маришальский колледж Абердинского университета Университет Падуи
Известный	Григорианский телескоп Коэффициенты Грегори Дифракционная решетка Основная теорема исчисления Интеграл от секущей функции
Научная карьера
Поля	Математика Астрономия
Учреждения	Университет Сент-Эндрюс Эдинбургский университет
Примечания
Племянник Александра Андерсона Дядя Дэвида Грегори

Джеймс Грегори ФРС (ноябрь 1638 — октябрь 1675) — шотландский математик и астроном . Его фамилия иногда пишется как Грегори , оригинальное шотландское написание. Он описал раннюю практическую конструкцию телескопа -рефлектора – григорианского телескопа – и добился успехов в тригонометрии , открыв представления бесконечных серий для нескольких тригонометрических функций.

В своей книге «Geometry Part Universalis» (1668 г.) Грегори дал как первое опубликованное утверждение, так и доказательство основной теоремы исчисления (изложенной с геометрической точки зрения и только для специального класса кривых, рассматриваемых в более поздних версиях теоремы), за что он был признан Исааком Барроу .

Биография

Грегори родился в 1638 году. Его мать Джанет была дочерью Джин и Дэвида Андерсонов , а его отцом был Джон Грегори. Священник Епископальной церкви Шотландии , Джеймс был младшим из троих детей, он родился в особняке в Друмоаке , Абердиншир , и первоначально получил домашнее образование у своей матери Джанет Андерсон (~ 1600–1668). Грегори наделила мать Тягу к геометрии , а ее дядя — Александр Андерсон (1582–1619) — был учеником и редактором французского математика Виета . После смерти отца в 1651 году ответственность за его образование взял на себя старший брат Давид. Он учился в Абердинской гимназии , а затем в Маришальском колледже в 1653–1657 годах, окончив AM в 1657 году.

В 1663 году он отправился в Лондон, где встретился с Джоном Коллинзом и шотландцем Робертом Мореем , одним из основателей Королевского общества . В 1664 году он отправился в Падуанский университет в Венецианской республике , пройдя через Фландрию по пути , Париж и Рим. В Падуе он жил в доме своего соотечественника Джеймса Кэдденхеда , профессора философии, и его обучал Стефано Анджели .

По возвращении в Лондон в 1668 году он был избран членом Королевского общества , а затем в конце 1668 года отправился в Сент-Эндрюс, чтобы занять свой пост первого королевского профессора математики в Университете Сент-Эндрюса , должность, созданную для него Карл II , вероятно, по просьбе Роберта Морея. Там, в Университете Сент-Эндрюс , он проложил первую линию меридиана по полу своей лаборатории в 1673 году, то есть за 200 лет до установления Гринвичского меридиана, и, таким образом, «возможно, сделав Сент-Эндрюс местом, где началось время».

Он последовательно был профессором Университета Сент-Эндрюс и Эдинбургского университета .

Он женился на Мэри, дочери Джорджа Джеймсона , художника и вдове Джона Бёрнета из Элрика, Абердин; их сын Джеймс был профессором физики в Королевском колледже в Абердине . Он был дедушкой Джона Грегори (FRS 1756); дядя Дэвида Грегори (FRS 1692) и брат Дэвида Грегори (1627–1720), врача и изобретателя.

Примерно через год после вступления на должность кафедры математики в Эдинбурге у Джеймса Грегори случился инсульт, когда он вместе со своими учениками наблюдал за спутниками Юпитера. Он умер несколько дней спустя в возрасте 36 лет.

Опубликованные работы

Истинная квадратура круга и гиперболы , 1667 г.

Оптика Продвижение

В Optica Promota , опубликованной в 1663 году, Грегори описал свою конструкцию телескопа -рефлектора , « григорианского телескопа ». Он также описал метод использования транзита Венеры для измерения расстояния Земли от Солнца, который позже был предложен Эдмундом Галлеем и принят за основу первого эффективного измерения астрономической единицы .

Истинная квадратура окружностей и гипербол

Прежде чем покинуть Падую, Грегори опубликовал Vera Circuli et Hyperbolae Quadratura (1667), в которой аппроксимировал площади круга и гиперболы сходящимися рядами:

[Джеймсу Грегори] нельзя отрицать авторство многих любопытных теорем об отношении круга к вписанным и описанным многоугольникам , а также их отношении друг к другу. С помощью этих теорем он дает с бесконечно меньшими трудностями, чем при помощи обычных вычислений,… меру круга и гиперболы (и, следовательно, построение логарифмов ) с точностью до двадцати десятичных знаков. По примеру Гюйгенса он дал также конструкции прямых, равных дугам окружности , и ошибка которых еще меньше.

первое доказательство фундаментальной теоремы исчисления , и открытие ряда Тейлора ». « Ему можно приписать и

Книга была переиздана в 1668 году с приложением Geometriae Pars объемы тел вращения , в котором Грегори объяснил, как можно определить .

Григорианский телескоп

Схема григорианского телескопа-рефлектора.

Основная статья: Григорианский телескоп

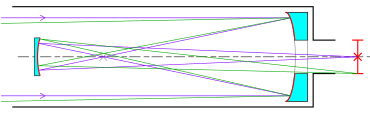
В своей книге Optica Promota 1663 года Джеймс Грегори описал свой телескоп-рефлектор , который стал известен под его именем, — григорианский телескоп. Грегори отметил, что телескоп-рефлектор с параболическим зеркалом исправит сферическую аберрацию , а также хроматическую аберрацию, наблюдаемую в телескопах-рефракторах . В своем проекте он также поместил вогнутое вторичное зеркало с эллиптической поверхностью за фокус параболического главного зеркала , отражая изображение обратно через отверстие в главном зеркале, где его можно было удобно просматривать. По его собственному признанию, Грегори не обладал практическими навыками и не мог найти оптика, способного его изготовить.

Конструкция телескопа привлекла внимание нескольких представителей научного сообщества, таких как Роберт Гук , оксфордский физик, который в конечном итоге построил телескоп 10 лет спустя, и сэр Роберт Морей , эрудит и член-основатель Королевского общества .

Григорианская конструкция телескопа сегодня используется редко, поскольку известно, что другие типы телескопов-рефлекторов более эффективны для стандартных приложений. Григорианская оптика также используется в радиотелескопах, таких как Аресибо , который имеет «григорианский купол».

Математика

Следующий отрывок взят из « Пантологии» . Новая (кабинетная) циклопедия (1813 г.)

Мистер Джеймс Грегори был человеком очень острого и проницательного гения. ... Самой блестящей частью его характера был его математический гений как изобретателя, который был первоклассным; как видно из... его изобретений и открытий, [которые включают] квадратуру круга и гиперболы, бесконечного сходящегося ряда; его метод преобразования кривых; геометрическая демонстрация ряда лорда Браункера для возведения в квадрат гиперболы — его демонстрация того, что линия меридиана аналогична шкале логарифмических тангенсов половинных дополнений широты; он также изобрел и продемонстрировал геометрически, с помощью гиперболы, очень простой сходящийся ряд для вычисления логарифмов; он послал мистеру Коллинзу решение знаменитой проблемы Кеплера бесконечным рядом; он открыл метод геометрического построения касательных к кривым без каких-либо предварительных вычислений; правило прямого и обратного метода касательных, основанное на том же принципе ( истощения ) с таковым у флюксий и мало чем отличается от него по способу применения; ряд для длины дуги окружности от касательной и наоборот; а также для секущего и логарифмического тангенса и секанса, и наоборот. Они, а также другие, для измерения длин эллиптических и гиперболических кривых, были отправлены мистеру Коллинзу в обмен на некоторые полученные от него ньютоновские работы , в которых он последовал элегантному примеру этого автора, излагая свои серии в простой форме. понятия, независимые друг от друга.

Другая работа

В письме 1671 года Джону Коллинзу Грегори дает в степенной ряд (используя современные обозначения) разложение семи функций ${\textstyle \arctan x}$ (часто называемая серией Грегори ), ${\textstyle \tan x,}$ ${\textstyle \sec x,}$ ${\textstyle \log \,\sec x,}$ обратная функция Гудермана ${\textstyle \log \,\tan {\tfrac {1}{2}}{\bigl (}x+{\tfrac {1}{2}}\pi {\bigr )}}$, ${\textstyle \operatorname {arcsec} {\bigl (}{\sqrt {2}}e^{x}{\bigr )},}$ и функция Гудермана ${\textstyle 2\arctan e^{x}-{\tfrac {1}{2}}\pi .}$

Есть свидетельства того, что он открыл метод взятия высших производных для вычисления степенного ряда, который был открыт Тейлором только в 1715 году, но не публиковал свои результаты, думая, что он всего лишь заново открыл «универсальный метод г-на Ньютона», который была основана на другой методике.

Джеймс Грегори обнаружил дифракционную решетку , пропуская солнечный свет через птичье перо и наблюдая возникающую дифракционную картину. В частности, он наблюдал расщепление солнечного света на составляющие цвета – это произошло через год после того, как Ньютон проделал то же самое с призмой , и это явление до сих пор оставалось весьма спорным.

Круглое колесо непригодно для неровных поверхностей, и Грегори разработал подходящее «адаптируемое колесо», используя преобразование Грегори .

Грегори, страстный сторонник Ньютона, позже имел с ним обширную дружескую переписку и включил его идеи в свое учение, идеи, которые в то время были спорными и считались весьма революционными.

Его именем назван кратер Грегори на Луне. Он был дядей математика Дэвида Грегори .

Работает

• 1663 г. - Optica promota (Развитие оптики), ссылка из Google Книги .
• 1667 - Vera Circuli et Hyperbolae Squaretura ( Истинный квадрат круга и гиперболы ) через Интернет-архив.
• 1668 г. - Exercitationesometricae (Геометрические упражнения), ссылка из Google Книги.
• 1668 – Geometriae pars Universalis (Универсальная часть геометрии)

См. также

• Телескоп Джеймса Грегори, Сент-Эндрюс
• Телескоп Грегора в обсерватории Тейде.
• Томас Рид
• Динс Корт

Дальнейшее чтение

• Тернбулл, Герберт Вестрен, изд. (1939). Джеймс Грегори; Том памяти трехсотлетия . Дж. Белл и сыновья для Королевского общества Эдинбурга .
• Тернбулл, Герберт Вестрен (1940–1941). «Ранние отношения Шотландии с Королевским обществом: И. Джеймс Грегори, FRS (1638–1675)» . Заметки и отчеты Лондонского королевского общества . 3 : 22–38. дои : 10.1098/rsnr.1940.0003 . JSTOR   531136 . S2CID   145801030 .
• Малет, Антони (1989). Исследования Джеймса Грегори (1638–1675) (доктор философии). Принстонский университет.

Внешние ссылки

• Тернбулл, HW (1938). «Трехсотлетие со дня рождения Джеймса Грегори» . Проверено 19 октября 2008 г.
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Джеймс Грегори» , Архив истории математики MacTutor , Университет Сент-Эндрюс
• Евклидово доказательство Джеймса Грегори фундаментальной теоремы исчисления при сходимости
• Публичные лекции Джеймса Грегори по религии и науке, Университет Сент-Эндрюс
• Джеймса Грегори (перевод на английский) « Optica Promota »
• » Джеймса Грегори « Универсальная часть геометрии » Грегори (английский перевод Эндрю Лихи « Geometriae Pars Universalis ).
• Джеймс Грегори (1663) Optica promota - цифровое факсимиле из библиотеки Линды Холл