Предел функции

$x$	${\frac {\sin x}{x}}$
1	0.841471...
0.1	0.998334...
0.01	0.999983...

Хотя функция ${\tfrac {\sin x}{x}}$ не определяется в нуле, поскольку $x$ становится все ближе и ближе к нулю, ${\tfrac {\sin x}{x}}$ становится сколь угодно близким к 1. Другими словами, предел ${\tfrac {\sin x}{x}},$ когда $x$ приближается к нулю, равно 1.

В математике предел функции — это фундаментальная концепция исчисления и анализа , касающаяся поведения этой функции вблизи определенного входного сигнала , который может находиться или не находиться в области определения функции.

Ниже приведены формальные определения, впервые разработанные в начале XIX века. Неформально, функция $f$ назначает выход $f (x)$ каждому входу $x$ . Мы говорим, что функция имеет предел $L$ на входе $p$ , если $f (x)$ становится всё ближе и ближе к $L$ по мере того, как $x$ приближается всё ближе и ближе к $p$ . Более конкретно, выходное значение может быть сделано сколь угодно близким к $L$ , если входные данные $f$ взяты достаточно близкими к $p$ . С другой стороны, если некоторые входные данные, очень близкие к $p,$ преобразуются в выходные данные, находящиеся на фиксированном расстоянии друг от друга, то мы говорим, что предела не существует .

Понятие предела имеет множество применений в современном исчислении . В частности, во многих определениях непрерывности используется концепция предела: грубо говоря, функция является непрерывной, если все ее пределы совпадают со значениями функции. Понятие предела появляется и в определении производной : в исчислении одной переменной это предельное значение наклона секущих линий к графику функции.

История [ править ]

Современная идея предела функции, хотя и неявно присутствовала в развитии исчисления 17-18 веков, восходит к Больцано , который в 1817 году представил основы техники эпсилон-дельта (см. (ε, δ)-определение предела ниже) для определения непрерывных функций. Однако при жизни его работы не были известны. ^[1]

В своей книге «Кур анализа» 1821 года Огюстен-Луи Коши обсуждал переменные величины, бесконечно малые величины и пределы, а также определял непрерывность $y=f(x)$ говоря, что бесконечно малое изменение $x$ обязательно приводит к бесконечно малому изменению $y$ , в то время как Грабинер утверждает, что он использовал строгое определение эпсилон-дельта в доказательствах. ^[2] В 1861 году Вейерштрасс впервые представил определение предела эпсилон-дельта в той форме, в которой оно обычно пишется сегодня. ^[3] Он также ввел обозначения ${\textstyle \lim }$ и ${\textstyle \textstyle \lim _{x\to x_{0}}\displaystyle .}$ ^[4]

Современное обозначение размещения стрелки ниже предельного символа принадлежит Харди , которое введено в его книге «Курс чистой математики» в 1908 году. ^[5]

Мотивация [ править ]

Представьте себе человека, идущего по ландшафту, представленному графиком $y = f (x)$ . Их горизонтальное положение определяется $x$ , во многом аналогично положению, заданному на карте местности или в глобальной системе позиционирования . Их высота задается координатой $y$ . Предположим, они идут к позиции $x = p$ , и по мере приближения к этой точке они заметят, что их высота приближается к определенному $L.$ значению Если бы их спросили о высоте, соответствующей $x = p$ , они бы ответили $y = L.$ :

Что же тогда значит, когда говорят, что их высота приближается к $L$ ? Это означает, что их высота становится все ближе и ближе к $L$ — за исключением возможной небольшой погрешности в точности. Например, предположим, что мы установили для нашего путешественника конкретную цель по точности: он должен находиться в пределах десяти метров от $L$ . Они сообщают, что действительно могут оказаться в пределах десяти метров по вертикали от $L$ что пока они находятся в пределах пятидесяти метров по горизонтали от $p$ , их высота всегда находится в пределах десяти метров от $L.$ , утверждая ,

Затем цель точности меняется: смогут ли они попасть в пределах одного вертикального метра? что они могут двигаться в пределах пяти метров по горизонтали от $p$ , их высота всегда будет оставаться в пределах одного метра от целевой высоты $L.$ Да, если предположить , Суммируя вышеупомянутую концепцию, мы можем сказать, что высота путешественника приближается к $L$ по мере того, как его горизонтальное положение приближается к $p$ , то есть для каждой цели целевой точности, какой бы маленькой она ни была, существует некоторая окрестность $p$ , где все (а не только некоторые) высоты соответствуют всем горизонтальным положениям, за исключением, возможно, самого горизонтального положения $p$ , в этой окрестности достигают этой цели точности.

Первоначальное неформальное утверждение теперь можно объяснить:

Пределом функции

f (x)

при

x

приближении

к p

является число

L

со следующим свойством: при любом целевом расстоянии от

L

существует расстояние от

p

, в пределах которого значения

f (x)

остаются в пределах целевого расстояния.

Фактически, это явное утверждение весьма близко к формальному определению предела функции со значениями в топологическом пространстве .

Точнее сказать, что

\lim _{x\to p}f(x)=L,

То есть, $f (x)$ можно сделать настолько близким к $L$ , насколько это необходимо, сделав $x$ достаточно близким, но не равным $p$ .

Следующие определения, известные как $(ε, δ)$ -определения, являются общепринятыми определениями предела функции в различных контекстах.

Функции одной переменной [ править ]

$(e, d)$ - определение предела [ редактировать ]

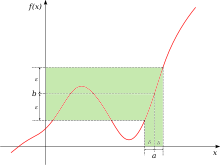
Предполагать $f:\mathbb {R} \rightarrow \mathbb {R}$ — функция, определенная на прямой , и существуют два действительных числа $p$ и $L.$ действительной Можно было бы сказать, что предел $f$ , когда $x$ приближается к $p$ , равен $L$ и записан ^[6]

\lim _{x\to p}f(x)=L,

или, альтернативно, скажем, $f (x)$ стремится к $L,$ поскольку $x$ стремится к $p$ , и записано:

f(x)\to L{\text{ as }}x\to p,

если выполняется следующее свойство: для каждого вещественного $ε > 0$ существует вещественное число $δ > 0$ такое, что для всех вещественных $x$ 0 $< | Икс - р | < δ$ подразумевает $| ж (Икс) - L | < е$ . ^[6] Символически,

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in \mathbb {R} )\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon ).

Например, мы можем сказать

\lim _{x\to 2}(4x+1)=9

потому что для любого вещественного

ε > 0

мы можем взять

δ = ε /4

, так что для всех вещественных

x

, если

0 < | х - 2 | < δ

, то

| 4 х + 1 - 9 | < е

.

Более общее определение применяется к функциям, определенным на подмножествах реальной линии. Пусть $S$ — подмножество $\mathbb {R} .$ Позволять $f:S\to \mathbb {R}$ быть вещественной функцией . Пусть $p$ — такая точка, что существует некоторый открытый интервал $(a, b)$ , содержащий $p$ с $(a,p)\cup (p,b)\subset S.$ Тогда говорят, что предел $f$ при $x$ приближении $к p$ равен $L$ , если:

Для каждого действительного

ε > 0

существует вещественное число

δ > 0

такое, что для всех

x \in (a, b)

,

0 < | Икс - р | < δ

означает, что

| ж (Икс) - L | < е

.

Или, символически:

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon ).

Например, мы можем сказать

\lim _{x\to 1}{\sqrt {x+3}}=2

потому что для любого действительного

ε > 0

мы можем взять

δ = ε

, так что для всех действительных

x \geq -3

, если

0 < | х - 1 | < δ

, то

| ж (Икс) - 2 | < е

. В этом примере

S = [-3, \infty)

содержит открытые интервалы вокруг точки 1 (например, интервал (0, 2)).

Здесь обратите внимание, что значение предела не зависит ни от того, $f$ определено ли $в точке p$ , ни от значения $f (p)$ — если оно определено. Например, пусть $f:[0,1)\cup (1,2]\to \mathbb {R} ,f(x)={\tfrac {2x^{2}-x-1}{x-1}}.$

\lim _{x\to 1}f(x)=3

потому что для любого

ε > 0

мы можем взять

δ = ε /2

, так что для всех действительных

x \neq 1

, если

0 < | х - 1 | < δ

, то

| ж (Икс) - 3 | < е

. Обратите внимание, что здесь

f (1)

не определена.

В действительности предел может существовать в $\{x\in \mathbb {R} \,|\,\exists (a,b)\subset \mathbb {R} \quad p\in (a,b){\text{ and }}(a,p)\cup (p,b)\subset S\},$ что равно $\operatorname {int} S\cup \operatorname {iso} S^{c},$ где $int S$ — внутренняя часть S $,$ а $iso S с$ являются изолированными точками дополнения к $S$ . В нашем предыдущем примере, где $S=[0,1)\cup (1,2],$ $\operatorname {int} S=(0,1)\cup (1,2),$ $\operatorname {iso} S^{c}=\{1\}.$ В частности, мы видим, что это определение предела допускает существование предела в 1, но не в 0 или 2.

Буквы $ε$ и $δ$ можно понимать как «ошибка» и «расстояние». Фактически, Коши использовал $ε$ как сокращение от слова «ошибка» в некоторых своих работах. ^[2] хотя в своем определении непрерывности он использовал бесконечно малую величину $\alpha$ а не $ε$ или $δ$ (см. Курс анализа ). В этих терминах погрешность ( ε ) измерения предельного значения можно сделать настолько малой, насколько это необходимо, за счет уменьшения расстояния ( δ ) до предельной точки. Как обсуждается ниже, это определение также работает для функций в более общем контексте. Идея о том, что $δ$ и $ε$ представляют расстояния, помогает предположить эти обобщения.

Существование и односторонние ограничения [ править ]

Альтернативно, $x$ может приближаться к $p$ сверху (справа) или снизу (слева), и в этом случае пределы можно записать как

\lim _{x\to p^{+}}f(x)=L

или

\lim _{x\to p^{-}}f(x)=L

соответственно. Если эти пределы существуют в точке p и там равны, то это можно назвать пределом f $точке (x)$ в $p$ . ^[7]Если односторонние пределы существуют в $точке p$ нет $, но неравны, то предела в точке p$ (т. е. предела в $точке p$ не существует). Если какой-либо односторонний предел не существует в $точке p$ , то и предел в точке $p$ также не существует.

Формальное определение следующее. Предел , $f$ когда $x$ приближается к $p$ сверху, равен $L$ , если:

Для любого

ε > 0

существует

δ > 0

такое, что всякий раз, когда

0 < x - p < δ

, мы имеем

| ж (Икс) - L | < е

.

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<x-p<\delta \implies |f(x)-L|<\varepsilon ).

Предел L $f$ , когда $x$ приближается к $p$ снизу, равен $,$ если:

Для каждого

ε > 0

существует

δ > 0

такое, что всякий раз, когда

0 < p - x < δ

, мы имеем

| ж (Икс) - L | < е

.

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in (a,b))\,(0<p-x<\delta \implies |f(x)-L|<\varepsilon ).

Если предел не существует, то колебание f $точке$ в $p$ не равно нулю.

Более общее определение с использованием предельных точек и подмножеств [ править ]

Пределы также могут быть определены путем подхода к подмножествам предметной области.

В общем: ^[8] Позволять $f:S\to \mathbb {R}$ быть вещественной функцией, определенной на некотором $S\subseteq \mathbb {R} .$ Пусть $p$ — предельная точка некоторого $T\subset S$ — то есть, $p$ — предел некоторой последовательности элементов $T,$ отличной от $p$ . Тогда мы говорим, что предел $f$ , когда $x$ приближается к $p$ от значений в $T$ , равен $L$ , записанный

\lim _{{x\to p} \atop {x\in T}}f(x)=L

если имеет место следующее:

Для любого

ε > 0

существует

δ > 0

такое, что для всех

x \in T

0

< | Икс - р | < δ

означает, что

| ж (Икс) - L | < е

.

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in T)\,(0<|x-p|<\delta \implies |f(x)-L|<\varepsilon ).

Обратите внимание: $T$ может быть любым подмножеством $S$ , областью определения $f$ . И предел может зависеть от выбора $T$ . Это обобщение включает в себя в качестве частных случаев пределы на интервале, а также левые пределы вещественных функций (например, если взять $T$ в качестве открытого интервала вида $(-\infty, a)$ ) и правые пределы (например, взяв $T$ в качестве открытого интервала формы $(a, \infty)$ ). Он также расширяет понятие односторонних пределов на включенные конечные точки (полу)замкнутых интервалов, поэтому функция квадратного корня $f(x)={\sqrt {x}}$ может иметь предел 0, когда $x$ приближается к 0 сверху:

\lim _{{x\to 0} \atop {x\in [0,\infty )}}{\sqrt {x}}=0

поскольку для любого

ε > 0

мы можем взять

δ = ε

такое, что для всех

x \geq 0

, если

0 < | Икс - 0 | < δ

, то

| ж (Икс) - 0 | < е

.

Это определение позволяет определить предел в предельных точках области $S$ подходящее подмножество $T$ , если выбрано , имеющее ту же предельную точку.

Примечательно, что предыдущее двустороннее определение работает $\operatorname {int} S\cup \operatorname {iso} S^{c},$ которое является подмножеством предельных точек $S$ .

Например, пусть $S=[0,1)\cup (1,2].$ Предыдущее двустороннее определение будет работать при $1\in \operatorname {iso} S^{c}=\{1\},$ но это не сработает при значениях 0 или 2, которые являются предельными точками $S$ .

Удаленные и неудаленные лимиты [ править ]

Определение предела, данное здесь, не зависит от того, как (или $ли) f$ определяется $в точке p$ . Бартл ^[9]называет это удаленным пределом , поскольку исключает значение $f$ в точке $p$ . Соответствующий неудаленный предел зависит от значения $f$ в точке $p$ , если $p$ находится в области определения $f$ . Позволять $f:S\to \mathbb {R}$ быть вещественной функцией. Неудаленный предел $f$ , когда $x$ приближается к $p$ , равен $L$ , если

Для любого

ε > 0

существует

δ > 0

такое, что для

x \in S

|

всех Икс - р | < δ

подразумевает

| ж (Икс) - L | < е

.

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(|x-p|<\delta \implies |f(x)-L|<\varepsilon ).

Определение то же самое, за исключением того, что окрестность $| Икс - р | < δ$ теперь включает точку $p$ , в отличие от удаленной окрестности $0 < | Икс - р | < δ$ . Это делает определение неудаляемого лимита менее общим. Одним из преимуществ работы с неудаляемыми пределами является то, что они позволяют сформулировать теорему о пределах композиции без каких-либо ограничений на функции (кроме существования их неудаляемых пределов). ^[10]

Бартл ^[9] отмечает, что, хотя под «пределом» некоторые авторы подразумевают неудаляемый лимит, удаленные лимиты являются наиболее популярными. ^[11]

Примеры [ править ]

Отсутствие одностороннего лимита(ов) [ править ]

Функция

f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\text{ for }}x<1\\0&{\text{ for }}x=1\\[2pt]{\frac {1}{10x-10}}&{\text{ for }}x>1\end{cases}}

не имеет предела при

x 0 = 1

(левый предел не существует из-за колебательного характера синусоидальной функции, а правый предел не существует из-за асимптотического поведения обратной функции, см. рисунок), но имеет предел по каждой второй

координате x

.

Функция

f(x)={\begin{cases}1&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}

(она же функция Дирихле ) не имеет предела ни в одной

координате x

.

Неравенство односторонних пределов [ править ]

Функция

f(x)={\begin{cases}1&{\text{ for }}x<0\\2&{\text{ for }}x\geq 0\end{cases}}

имеет предел в каждой ненулевой

координате x

(предел равен 1 для отрицательного

x

и равен 2 для положительного

x

). Предела при

x = 0

не существует (левый предел равен 1, а правый предел равен 2).

Ограничения только в одной точке [ править ]

Функции

f(x)={\begin{cases}x&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}

и

f(x)={\begin{cases}|x|&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}

оба имеют предел при

x = 0

и он равен 0.

Пределы в счетном числе точек [ править ]

Функция

f(x)={\begin{cases}\sin x&x{\text{ irrational }}\\1&x{\text{ rational }}\end{cases}}

имеет предел в любой

координате x

вида

{\tfrac {\pi }{2}}+2n\pi ,

где

n

— любое целое число.

Пределы, связанные с бесконечностью

Пределы на бесконечности [ править ]

Позволять $f:S\to \mathbb {R}$ быть функцией, определенной на $S\subseteq \mathbb {R} .$ Пределом $f$ , когда $x$ приближается к бесконечности, является $L$ , обозначаемый

\lim _{x\to \infty }f(x)=L,

Значит это:

Для каждого

ε > 0

существует

c > 0

такое, что всякий раз, когда

+ x > c

, мы имеем

| ж (Икс) - L | < е

.

(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(x>c\implies |f(x)-L|<\varepsilon ).

Аналогично, предел $f$ при $приближении x$ к минус бесконечности равен $L$ , обозначаемый

\lim _{x\to -\infty }f(x)=L,

Значит это:

Для каждого

ε > 0

существует

c > 0

такой, что всякий раз, когда

x < - c

, мы имеем

| ж (Икс) - L | < е

.

(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(x<-c\implies |f(x)-L|<\varepsilon ).

Например,

\lim _{x\to \infty }\left(-{\frac {3\sin x}{x}}+4\right)=4

потому что для любого

ε > 0

мы можем взять

c = 3/ ε

такое, что для всех действительных

x

, если

x > c

, то

| ж (Икс) - 4 | < е

.

Другой пример заключается в том, что

\lim _{x\to -\infty }e^{x}=0

потому что для любого

ε > 0

мы можем взять

c = max{1, -ln(ε)}

так, что для всех вещественных

x

, если

x < - c

, то

| ж (Икс) - 0 | < е

.

Бесконечные пределы [ править ]

Для функции, значения которой неограниченно растут, функция расходится и обычного предела не существует. Однако в этом случае можно ввести пределы с бесконечными значениями.

Позволять $f:S\to \mathbb {R}$ быть функцией, определенной на $S\subseteq \mathbb {R} .$ Утверждение, что предел $f$ при $x$ приближении $к p$ равен бесконечности , обозначается

\lim _{x\to p}f(x)=\infty ,

Значит это:

Для каждого

N > 0

существует

δ > 0

такое, что всякий раз, когда

0 < | Икс - р | < δ

, мы имеем

f (x) > N

.

(\forall N>0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies f(x)>N).

Утверждение, что предел $f$ при $x$ приближении $к p$ равен минус бесконечности , обозначается

\lim _{x\to p}f(x)=-\infty ,

Значит это:

Для каждого

N > 0

существует

δ > 0

такое, что всякий раз, когда

0 < | Икс - р | < δ

, мы имеем

ж (Икс) < - N

.

(\forall N>0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies f(x)<-N).

Например,

\lim _{x\to 1}{\frac {1}{(x-1)^{2}}}=\infty

потому что для каждого

N > 0

мы можем взять

{\textstyle \delta ={\tfrac {1}{{\sqrt {N}}\delta }}={\tfrac {1}{\sqrt {N}}}}

такой, что для всех действительных

x > 0

, если

0 < x - 1 < δ

, то

f (x) > N

.

Эти идеи можно использовать вместе для создания определений различных комбинаций, таких как

\lim _{x\to \infty }f(x)=\infty ,

или

\lim _{x\to p^{+}}f(x)=-\infty .

Например,

\lim _{x\to 0^{+}}\ln x=-\infty

потому что для любого

N > 0

мы можем взять

δ = e - Н

такой, что для всех действительных

x > 0

, если

0 < x - 0 < δ

, то

f (x) < - N

.

Пределы, включающие бесконечность, связаны с понятием асимптот .

Эти понятия предела пытаются дать интерпретацию пределов на бесконечности в метрическом пространстве. Фактически, они согласуются с определением предела в топологическом пространстве, если

окрестность −∞ определяется как содержащая интервал $[-\infty, c)$ для некоторого $c\in \mathbb {R} ,$
окрестность ∞ определяется как содержащая интервал $(c, \infty]$ , где $c\in \mathbb {R} ,$ и
окрестности $a\in \mathbb {R}$ определяется обычным образом метрическое пространство $\mathbb {R} .$

В этом случае, ${\overline {\mathbb {R} }}$ является топологическим пространством и любая функция вида $f:X\to Y$ с $X,Y\subseteq {\overline {\mathbb {R} }}$ подлежит топологическому определению предела. Обратите внимание, что с помощью этого топологического определения легко определить бесконечные пределы в конечных точках, которые не были определены выше в метрическом смысле.

Альтернативное обозначение [ править ]

Многие авторы ^[12]позволяют использовать проективно расширенную действительную линию как способ включения бесконечных значений, а также расширенную действительную линию . В этих обозначениях расширенная действительная линия задается как $\mathbb {R} \cup \{-\infty ,+\infty \}$ а проективно продолженная действительная линия равна $\mathbb {R} \cup \{\infty \}$ где окрестность точки ∞ представляет собой множество вида $\{x:|x|>c\}.$ Преимущество состоит в том, что для охвата всех случаев достаточно всего трех определений пределов (левого, правого и центрального). Как указано выше, для абсолютно строгого учета нам потребуется рассмотреть 15 отдельных случаев для каждой комбинации бесконечностей (пять направлений: −∞, левое, центральное, правое и +∞; три границы: −∞, конечная или + ∞). Есть и примечательные подводные камни. Например, при работе с расширенной действительной линией $x^{-1}$ не имеет центрального предела (что нормально):

\lim _{x\to 0^{+}}{1 \over x}=+\infty ,\quad \lim _{x\to 0^{-}}{1 \over x}=-\infty .

Напротив, при работе с проективной действительной линией бесконечности (как и 0) не имеют знака, поэтому центральный предел действительно существует в этом контексте:

\lim _{x\to 0^{+}}{1 \over x}=\lim _{x\to 0^{-}}{1 \over x}=\lim _{x\to 0}{1 \over x}=\infty .

На самом деле существует множество конфликтующих между собой формальных систем. В некоторых приложениях численного дифференцирования и интегрирования удобно иметь, например, нули со знаком . Простая причина связана с обратным утверждением $\lim _{x\to 0^{-}}{x^{-1}}=-\infty ,$ а именно, это удобно для $\lim _{x\to -\infty }{x^{-1}}=-0$ считать правдой. Такие нули можно рассматривать как приближение к бесконечно малым .

для рациональных функций Пределы на бесконечности

Существует три основных правила оценки пределов на бесконечности для рациональной функции. $f(x)={\tfrac {p(x)}{q(x)}}$ (где $p$ и $q$ — полиномы):

Если степень p $q$ больше степени $,$ то предел равен положительной или отрицательной бесконечности в зависимости от знаков старших коэффициентов;
Если степени $p$ и $q$ равны, пределом является старший коэффициент $p$ , деленный на старший коэффициент $q$ ;
Если степень $p$ меньше степени $q$ , предел равен 0.

Если предел на бесконечности существует, он представляет собой горизонтальную асимптоту $y = L.$ при Полиномы не имеют горизонтальных асимптот; однако такие асимптоты могут возникать и с рациональными функциями.

Функции более чем одной переменной [ править ]

Обычные ограничения [ править ]

Отметив, что $| Икс - р |$ представляет расстояние , определение предела может быть распространено на функции более чем одной переменной. В случае функции $f:S\times T\to \mathbb {R}$ определено на $S\times T\subseteq \mathbb {R} ^{2},$ мы определили предел следующим образом: предел $f$ при $(x, y)$ приближении $к (p, q)$ равен $L$ , записанный

\lim _{(x,y)\to (p,q)}f(x,y)=L

если выполняется следующее условие:

Для каждого

ε > 0

существует

δ > 0

такое, что для всех

x

в

S

и

y

в

T

, всякий раз, когда

{\textstyle 0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta ,}

у нас есть

| ж (Икс, y) - L | < ε

, ^[13]

или формально:

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta \implies |f(x,y)-L|<\varepsilon )).

Здесь ${\textstyle {\sqrt {(x-p)^{2}+(y-q)^{2}}}}$ — евклидово расстояние между $(x, y)$ и $(p, q)$ . (Фактически это можно заменить любой нормой $| | (x, y) - (p, q) | |$ и распространить на любое количество переменных.)

Например, мы можем сказать

\lim _{(x,y)\to (0,0)}{\frac {x^{4}}{x^{2}+y^{2}}}=0

потому что для каждого

ε > 0

мы можем взять

{\textstyle \delta ={\sqrt {\varepsilon }}}

такой, что для всех действительных

x \neq 0

и вещественных

y \neq 0

, если

{\textstyle 0<{\sqrt {(x-0)^{2}+(y-0)^{2}}}<\delta ,}

тогда

| ж (Икс, y) - 0 | < е

.

Как и в случае с одной переменной, значение $f$ в $(p, q)$ не имеет значения в этом определении предела.

Для существования такого многовариантного предела это определение требует, чтобы значение $f$ приближалось к $L$ вдоль каждого возможного пути, приближающегося к $(p, q)$ . ^[14] В приведенном выше примере функция

f(x,y)={\frac {x^{4}}{x^{2}+y^{2}}}

удовлетворяет этому условию. В этом можно убедиться, рассматривая полярные координаты

(x,y)=(r\cos \theta ,r\sin \theta )\to (0,0),

который дает

\lim _{r\to 0}f(r\cos \theta ,r\sin \theta )=\lim _{r\to 0}{\frac {r^{4}\cos ^{4}\theta }{r^{2}}}=\lim _{r\to 0}r^{2}\cos ^{4}\theta .

Здесь

θ = θ (r)

— функция от r , которая управляет формой пути, по которому

f

приближается к

(p, q)

. Поскольку

cos θ

ограничен между [−1, 1] по сэндвич-теореме , этот предел стремится к 0.

Напротив, функция

f(x,y)={\frac {xy}{x^{2}+y^{2}}}

не имеет предела в

(0, 0)

. Пройдя путь

(x, y) = (t, 0) \to (0, 0)

, получаем

\lim _{t\to 0}f(t,0)=\lim _{t\to 0}{\frac {0}{t^{2}}}=0,

идя по пути

(x, y) = (t, t) \to (0, 0)

, мы получаем

\lim _{t\to 0}f(t,t)=\lim _{t\to 0}{\frac {t^{2}}{t^{2}+t^{2}}}={\frac {1}{2}}.

Поскольку эти два значения не совпадают, $f$ не стремится к одному значению, когда $(x, y)$ приближается к $(0, 0)$ .

Множественные ограничения [ править ]

Хотя он используется реже, существует еще один тип предела для функции с несколькими переменными, известный как множественный предел . Для функции с двумя переменными это двойной предел . ^[15] Позволять $f:S\times T\to \mathbb {R}$ быть определены на $S\times T\subseteq \mathbb {R} ^{2},$ мы говорим, что двойной предел $f$ , когда $x$ приближается к $p$ , а $y$ приближается к $q$ , равен $L$ , записанный

\lim _{{x\to p} \atop {y\to q}}f(x,y)=L

если выполняется следующее условие:

Для каждого

ε > 0

существует

δ > 0

такое, что для всех

x

в

S

и

y

в

T

всякий раз, когда

0 < | Икс - р | < δ

и

0 < | у - д | < δ

, мы имеем

| ж (Икс, y) - L | < е

. ^[15]

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,((0<|x-p|<\delta )\land (0<|y-q|<\delta )\implies |f(x,y)-L|<\varepsilon ).

Для существования такого двойного предела это определение требует, чтобы значение $f$ приближалось к $L$ вдоль каждого возможного пути, приближающегося к $(p, q)$ , исключая две линии $x = p$ и $y = q$ . В результате кратный предел является более слабым понятием, чем обычный предел: если обычный предел существует и равен $L$ , то кратный предел существует и также $L.$ равен Обратное неверно: существование множественных пределов не означает существования обычного предела. Рассмотрим пример

f(x,y)={\begin{cases}1\quad {\text{for}}\quad xy\neq 0\\0\quad {\text{for}}\quad xy=0\end{cases}}

где

\lim _{{x\to 0} \atop {y\to 0}}f(x,y)=1

но

\lim _{(x,y)\to (0,0)}f(x,y)

не существует.

Если область определения $f$ ограничена $(S\setminus \{p\})\times (T\setminus \{q\}),$ тогда два определения пределов совпадают. ^[15]

Множественные ограничения на бесконечности [ править ]

Концепция множественного предела может распространяться на предел на бесконечности, аналогично функции с одной переменной. Для $f:S\times T\to \mathbb {R} ,$ мы говорим, что двойной предел $f$ , когда $x$ и $y$ приближаются к бесконечности, равен $L$ , записанный

\lim _{{x\to \infty } \atop {y\to \infty }}f(x,y)=L

если выполняется следующее условие:

Для каждого

ε > 0

существует

c > 0

такой, что для всех

x

в

S

и

y

в

T

, когда

x > c

и

y > c

, мы имеем

| ж (Икс, y) - L | < е

.

(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(\forall y\in T)\,((x>c)\land (y>c)\implies |f(x,y)-L|<\varepsilon ).

Мы говорим, что двойной предел $f$ при $приближении x$ и $y$ к минус бесконечности равен $L$ , записанный

\lim _{{x\to -\infty } \atop {y\to -\infty }}f(x,y)=L

если выполняется следующее условие:

Для каждого

ε > 0

существует

c > 0

такой, что

x

в

S

и

y

в

T

, всякий раз, когда

x < - c

и

y < - c

, мы имеем

| ж (Икс, y) - L | < е

.

(\forall \varepsilon >0)\,(\exists c>0)\,(\forall x\in S)\,(\forall y\in T)\,((x<-c)\land (y<-c)\implies |f(x,y)-L|<\varepsilon ).

Поточечные пределы и равномерные пределы [ править ]

Позволять $f:S\times T\to \mathbb {R} .$ Вместо того, чтобы брать предел как $(x, y) \to (p, q)$ , мы можем рассмотреть возможность использования предела только одной переменной, скажем, $x \to p$ , чтобы получить функцию одной переменной от $y$ , а именно $g:T\to \mathbb {R} .$ Фактически, этот ограничивающий процесс может осуществляться двумя различными способами. Первый из них называется поточечным пределом . Мы говорим, что поточечный предел $f$ при $x$ приближении $к p$ равен $g$ , обозначаемый

\lim _{x\to p}f(x,y)=g(y),

или

\lim _{x\to p}f(x,y)=g(y)\;\;{\text{pointwise}}.

В качестве альтернативы мы можем сказать, $что f$ стремится к $g$ поточечно, когда $x$ приближается к $p$ , что обозначается

f(x,y)\to g(y)\;\;{\text{as}}\;\;x\to p,

или

f(x,y)\to g(y)\;\;{\text{pointwise}}\;\;{\text{as}}\;\;x\to p.

Этот предел существует, если выполняется следующее:

Для каждого

ε > 0

и каждого фиксированного

y

в

T

существует

δ (ε, y) > 0

такое, что для всех

x

в

S

, всякий раз, когда

0 < | Икс - р | < δ

, мы имеем

| ж (Икс, y) - грамм (y) | < е

. ^[16]

(\forall \varepsilon >0)\,(\forall y\in T)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f(x,y)-g(y)|<\varepsilon ).

Здесь $δ = δ (ε, y)$ является функцией как $ε$ , так и $y$ . Каждый $δ$ выбирается для конкретной точки $y$ . Следовательно, мы говорим, что предел поточечен по $y$ . Например,

f(x,y)={\frac {x}{\cos y}}

имеет поточечный предел постоянной нулевой функции

\lim _{x\to 0}f(x,y)=0(y)\;\;{\text{pointwise}}

потому что для каждого фиксированного

y

предел явно равен 0. Этот аргумент неверен, если

y

не фиксирован: если

y

очень близко к

π /2

, значение дроби может отклоняться от 0.

Это приводит к другому определению предела, а именно к равномерному пределу . Мы говорим, что равномерный предел $f$ на $T$ при $x$ приближении $к p$ равен $g$ , обозначаемый

{\underset {{x\to p} \atop {y\in T}}{\mathrm {unif} \lim \;}}f(x,y)=g(y),

или

\lim _{x\to p}f(x,y)=g(y)\;\;{\text{uniformly on}}\;T.

В качестве альтернативы мы можем сказать, $что f$ стремится к $g$ равномерно на $T$ , когда $x$ приближается к $p$ , что обозначается

f(x,y)\rightrightarrows g(y)\;{\text{on}}\;T\;\;{\text{as}}\;\;x\to p,

или

f(x,y)\to g(y)\;\;{\text{uniformly on}}\;T\;\;{\text{as}}\;\;x\to p.

Этот предел существует, если выполняется следующее:

Для каждого

ε > 0

существует

δ (ε) > 0

такое, что для всех

x

в

S

и

y

в

T

, всякий раз, когда

0 < | Икс - р | < δ

, мы имеем

| ж (Икс, y) - грамм (y) | < е

. ^[16]

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,(0<|x-p|<\delta \implies |f(x,y)-g(y)|<\varepsilon ).

Здесь $δ = δ (ε)$ является функцией только $ε$ , но не $y$ . Другими словами, δ ко равномерно применимо всем $y$ в $T$ . Следовательно, мы говорим, что предел равномерен по $y$ . Например,

f(x,y)=x\cos y

имеет равномерный предел постоянной нулевой функции

\lim _{x\to 0}f(x,y)=0(y)\;\;{\text{ uniformly on}}\;\mathbb {R}

потому что для всех реальных

y

y

cos]

ограничен между

[-1, 1

. Следовательно, независимо от того, как

ведет себя y

, мы можем использовать сэндвич-теорему , чтобы показать, что предел равен 0.

Итерированные пределы [ править ]

Позволять $f:S\times T\to \mathbb {R} .$ Мы можем рассмотреть возможность ограничения только одной переменной, скажем, $x \to p$ , чтобы получить функцию одной переменной от $y$ , а именно $g:T\to \mathbb {R} ,$ а затем возьмем предел по другой переменной, а именно $\to q,$ чтобы получить число $L.$ y Символически,

\lim _{y\to q}\lim _{x\to p}f(x,y)=\lim _{y\to q}g(y)=L.

Этот предел известен как повторный предел функции многих переменных. ^[17] Порядок взятия пределов может повлиять на результат, т.е.

\lim _{y\to q}\lim _{x\to p}f(x,y)\neq \lim _{x\to p}\lim _{y\to q}f(x,y)

в общем.

Достаточное условие равенства даёт теорема Мура-Осгуда , которая требует предела $\lim _{x\to p}f(x,y)=g(y)$ быть равномерным на $T$ . ^[18]

Функции в метрических пространствах [ править ]

Предположим, что $и$ N $—$ подмножества метрических пространств $A$ и $B$ соответственно, и $f : M \to N$ определено между $M$ и $N$ , причем $x \in M$ , $p$ предельная точка M $и$ L $M \in N.$ — Говорят, что предел $f$ при $x$ приближении $к p$ равен $L$ , и пишут

\lim _{x\to p}f(x)=L

если выполняется следующее свойство:

Для каждого

ε > 0

существует

δ > 0

такое, что для всех точек

x \in M

из

0 < d A (x, p) < δ

следует

d B (f (x), L) < ε

. ^[19]

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in M)\,(0<d_{A}(x,p)<\delta \implies d_{B}(f(x),L)<\varepsilon ).

Опять же, обратите внимание, что $p$ не обязательно должен находиться в области определения $f$ не $, а L$ обязательно должен находиться в диапазоне $f$ , и даже если $f (p)$ оно не обязательно должно быть равно $L.$ определено ,

Евклидова метрика [ править ]

Предел в евклидовом пространстве является прямым обобщением пределов векторных функций . Например, мы можем рассмотреть функцию $f:S\times T\to \mathbb {R} ^{3}$ такой, что

f(x,y)=(f_{1}(x,y),f_{2}(x,y),f_{3}(x,y)).

Тогда в обычной метрике евклидовой

\lim _{(x,y)\to (p,q)}f(x,y)=(L_{1},L_{2},L_{3})

если имеет место следующее:

Для каждого

ε > 0

существует

δ > 0

такое, что для

x

в

S

и

y

в

T

всех

{\textstyle 0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta }

подразумевает

{\textstyle {\sqrt {(f_{1}-L_{1})^{2}+(f_{2}-L_{2})^{2}+(f_{3}-L_{3})^{2}}}<\varepsilon .}

^[20]

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(\forall y\in T)\,\left(0<{\sqrt {(x-p)^{2}+(y-q)^{2}}}<\delta \implies {\sqrt {(f_{1}-L_{1})^{2}+(f_{2}-L_{2})^{2}+(f_{3}-L_{3})^{2}}}<\varepsilon \right).

В этом примере рассматриваемая функция представляет собой конечномерную векторную функцию. В этом случае предельная теорема для вектор-функции гласит, что если предел каждого компонента существует, то предел вектор-функции равен вектору, каждый компонент которого принимает предел: ^[20]

\lim _{(x,y)\to (p,q)}{\Bigl (}f_{1}(x,y),f_{2}(x,y),f_{3}(x,y){\Bigr )}=\left(\lim _{(x,y)\to (p,q)}f_{1}(x,y),\lim _{(x,y)\to (p,q)}f_{2}(x,y),\lim _{(x,y)\to (p,q)}f_{3}(x,y)\right).

Манхэттенская метрика [ править ]

Можно также рассмотреть пространства, отличные от евклидова. Примером может служить пространство Манхэттена. Учитывать $f:S\to \mathbb {R} ^{2}$ такой, что

f(x)=(f_{1}(x),f_{2}(x)).

Тогда по метрике манхэттенской

\lim _{x\to p}f(x)=(L_{1},L_{2})

если имеет место следующее:

Для каждого

ε > 0

существует

δ > 0

такое, что для всех

x

в

S

0

< | Икс - р | < δ

подразумевает

| ж 1 - L 1 | + | ж 2 - L 2 | < е

.

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies |f_{1}-L_{1}|+|f_{2}-L_{2}|<\varepsilon ).

Поскольку это тоже конечномерная вектор-функция, применима и сформулированная выше предельная теорема. ^[21]

Единая метрика [ править ]

Наконец, мы обсудим предел в функциональном пространстве , которое имеет бесконечные измерения. Рассмотрим функцию $f (x, y)$ в функциональном пространстве $S\times T\to \mathbb {R} .$ Мы хотим выяснить, как $x$ приближается к $p$ , как $f (x, y)$ будет стремиться к другой функции $g (y)$ , которая находится в функциональном пространстве $T\to \mathbb {R} .$ «Близость» в этом функциональном пространстве может быть измерена с помощью единой метрики . ^[22] Тогда мы скажем, что равномерный предел $f$ на $T$ при $x$ приближении $к p$ равен $g$ и напишем

{\underset {{x\to p} \atop {y\in T}}{\mathrm {unif} \lim \;}}f(x,y)=g(y),

или

\lim _{x\to p}f(x,y)=g(y)\;\;{\text{uniformly on}}\;T,

если имеет место следующее:

Для каждого

ε > 0

существует

δ > 0

такое, что для всех

x

в

S

0

< | Икс - р | < δ

подразумевает

\sup _{y\in T}|f(x,y)-g(y)|<\varepsilon .

(\forall \varepsilon >0)\,(\exists \delta >0)\,(\forall x\in S)\,(0<|x-p|<\delta \implies \sup _{y\in T}|f(x,y)-g(y)|<\varepsilon ).

Фактически можно видеть, что это определение эквивалентно определению равномерного предела функции многих переменных, введенному в предыдущем разделе.

Функции в топологических пространствах [ править ]

Предположим, что $X$ и $Y$ — топологические пространства, а $Y$ — хаусдорфово пространство . Пусть $p$ — точка Ω $\subseteq X$ и $L \in Y.$ предельная Для функции $f : Ω \to Y$ говорят, что предел $f$ при $x$ приближении $к p$ равен $L$ , записанный

\lim _{x\to p}f(x)=L,

если выполняется следующее свойство:

Для каждой открытой окрестности

V

точки

L

существует открытая окрестность

U

точки

p

такая, что

f (U \cap Ω - {p}) \subseteq V

.

Эту последнюю часть определения можно также сформулировать так: «существует открытая проколотая окрестность $U$ точки $p$ такая, что $f (U \cap Ω) \subseteq V$ ».

Область определения $f$ не обязательно должна содержать $p$ . Если да, то значение $f$ в точке $p$ не имеет отношения к определению предела. В частности, если областью определения $f$ является $X - {p}$ (или все $X$ ), то предел $f$ при $x \to p$ существует и равен $L$ для всех подмножеств $Ω$ X $p$ с предельной $точкой$ , если предел ограничения $f$ на $Ω$ существует и равен $L$ . Иногда этот критерий используют для установления отсутствия двустороннего предела функции на $\mathbb {R}$ показывая, что односторонние пределы либо не существуют, либо не согласуются друг с другом. Такой взгляд является фундаментальным в области общей топологии , где пределы и непрерывность в точке определяются в терминах специальных семейств подмножеств, называемых фильтрами , или обобщенных последовательностей, известных как сети .

Альтернативно, требование, чтобы $Y$ было хаусдорфовым пространством, можно смягчить до предположения, что $Y$ — общее топологическое пространство, но тогда предел функции может быть неединственным. В частности, уже можно говорить не о пределе функции в точке, а о пределе или множестве пределов в точке.

Функция непрерывна в предельной точке $p$ и в своей области определения тогда и только тогда, когда $f (p)$ является ( или, в общем случае, a ) пределом $f (x)$ , когда $x$ стремится к $p$ .

Существует еще один тип предела функции, а именно последовательный предел . Пусть $f : X \to Y$ — отображение топологического пространства $X$ в хаусдорфово пространство $Y$ , $p \in X$ предельная точка $X$ и $L \in Y.$ — Последовательный предел $f$ при $стремлении x$ к $p$ равен $L$ , если

Для каждой последовательности (

x n

) из

X - {p}

, которая сходится к

p

, последовательность

f (x n)

сходится к

L

.

Если $L$ является пределом (в указанном выше смысле) $f$ при $x$ приближении $к p$ , то это также последовательный предел, однако в общем случае обратное не обязательно. Если, кроме того, $,$ то X метризуемо L $является$ последовательным пределом $f$ при $x$ приближении $к p$ тогда и только тогда, когда это предел (в указанном выше смысле) $f$ при $x$ приближении $к p$ .

Другие характеристики [ править ]

С точки зрения последовательностей [ править ]

Для функций на реальной прямой один из способов определить предел функции — это предел последовательностей. (Это определение обычно приписывают Эдуарду Гейне .) В такой обстановке:

\lim _{x\to a}f(x)=L

тогда и только тогда, когда для всех последовательностей

x n

(где

x n

не равен

a

для всех

n

), сходящихся к

a,

последовательность

f (x n)

сходится к

L

. показал В 1916 году Серпинский , что доказательство эквивалентности этого определения и приведенного выше определения требует и эквивалентно слабой форме аксиомы выбора . последовательности

x n

Обратите внимание, что для определения того, что означает сходимость

к a,

требуется метод эпсилон, дельта .

Подобно определению Вейерштрасса, более общее определение Гейне применимо к функциям, определенным на подмножествах вещественной прямой. Пусть $f$ — вещественная функция с областью определения $Dm (f)$ . Пусть $a$ — предел последовательности элементов из $Dm ( f ) \ { a }.$ Тогда предел (в этом смысле) $f$ равен $L$ , когда $x$ приближается к $p$ если для каждой последовательности $x n ∈ Dm ( f ) \ { a }$ (так что для всех $n$ n $x a$ не равен $a$ ), которая сходится к $,$ последовательность $f (x n)$ сходится к $L$ . Это то же самое, что определение последовательного предела в предыдущем разделе, полученное при рассмотрении подмножества $Dm (f)$ из $\mathbb {R}$ как метрическое пространство с индуцированной метрикой.

В нестандартном расчете [ править ]

В нестандартном исчислении предел функции определяется следующим образом:

\lim _{x\to a}f(x)=L

тогда и только тогда, когда для всех

x\in \mathbb {R} ^{*},

f^{*}(x)-L

бесконечно мало, если

x - a

бесконечно мало. Здесь

\mathbb {R} ^{*}

— гипердействительные числа , а

f*

— естественное расширение

f

до нестандартных действительных чисел. Кейслер доказал, что такое гиперреальное определение предела уменьшает сложность квантора на два квантора. ^[23] С другой стороны, Хрбачек пишет, что для того, чтобы определения были действительными для всех гипердействительных чисел, они должны быть неявно основаны на методе ε-δ, и утверждает, что с педагогической точки зрения надежда на то, что нестандартное исчисление может быть без ε-δ методов невозможно реализовать в полной мере. ^[24]Баащик и др. подробно опишите полезность микронепрерывности для разработки прозрачного определения единообразной непрерывности и охарактеризуйте критику Хрбачека как «сомнительную жалобу». ^[25]

С точки зрения близости [ править ]

На международном математическом конгрессе 1908 года Ф. Рисс представил альтернативный способ определения пределов и непрерывности понятия, названного «близостью». ^[26] Точка $x$ определяется как находящаяся рядом с множеством $A\subseteq \mathbb {R}$ если для любого $r > 0$ существует точка $a \in A$ такая, что $| Икс - а | < р$ . В этой обстановке

\lim _{x\to a}f(x)=L

тогда и только тогда, когда для всех

A\subseteq \mathbb {R} ,

L

находится рядом

с f (A)

когда

a

находится рядом с

A.

, Здесь

f (A)

— множество

\{f(x)|x\in A\}.

Это определение также можно распространить на метрические и топологические пространства.

Отношение преемственности к

Понятие предела функции очень тесно связано с понятием непрерывности. Функция $f$ называется непрерывной в точке $c,$ если она определена в точке $c$ и ее значение в точке $c$ равно пределу функции $f$ при $x$ приближении $к c$ :

\lim _{x\to c}f(x)=f(c).

(Здесь мы предположили, что

c

является предельной точкой области определения

f

.)

Свойства [ править ]

Если функция $f$ вещественнозначна, то предел $f$ в $точке p$ равен $L$ тогда и только тогда, когда и правый предел, и левый предел $f$ в точке $p$ существуют и равны $L$ . ^[27]

Функция $f$ непрерывна тогда и только тогда , в $точке p$ когда предел $f (x)$ при $x$ приближении $к p$ существует и равен $f (p)$ . Если $f : M \to N$ — функция между метрическими пространствами $M$ и $N$ , то это эквивалентно тому, что $f$ преобразует каждую последовательность из $M$ , которая сходится к $p$ , в последовательность из $N$ , которая сходится к $f (p)$ .

Если $N$ — нормированное векторное пространство , то предельная операция линейна в следующем смысле: если предел $f (x)$ , когда $x$ приближается к $p$ , равен $L$ , а предел $g (x)$ , когда $x$ приближается к $p$ , равен $P$ , то предел $f (x) + g (x)$ при $x$ приближении $к p$ равен $L + P$ . Если $a$ является скаляром из базового поля , то пределом $af (x)$ при $x$ приближении $к p$ является $aL$ .

Если $f$ и $g$ — вещественные (или комплекснозначные) функции, то переход к пределу операции над $f (x)$ и $g (x)$ (например, $f + g$ , $f - g$ , $f \times g$ , $f / г$ , $ж г$ ) при определенных условиях совместимо с действием пределов $f (x)$ и $g (x)$ . Этот факт часто называют алгебраической предельной теоремой . Основным условием применения следующих правил является наличие пределов в правых частях уравнений (другими словами, эти пределы представляют собой конечные значения, включая 0). Кроме того, тождество деления требует, чтобы знаменатель в правой части был ненулевым (деление на 0 не определено), а тождество возведения в степень требует, чтобы основание было положительным или нулевым, а показатель степени положителен (конечный ).

{\begin{array}{lcl}\displaystyle \lim _{x\to p}(f(x)+g(x))&=&\displaystyle \lim _{x\to p}f(x)+\lim _{x\to p}g(x)\\\displaystyle \lim _{x\to p}(f(x)-g(x))&=&\displaystyle \lim _{x\to p}f(x)-\lim _{x\to p}g(x)\\\displaystyle \lim _{x\to p}(f(x)\cdot g(x))&=&\displaystyle \lim _{x\to p}f(x)\cdot \lim _{x\to p}g(x)\\\displaystyle \lim _{x\to p}(f(x)/g(x))&=&\displaystyle {\lim _{x\to p}f(x)/\lim _{x\to p}g(x)}\\\displaystyle \lim _{x\to p}f(x)^{g(x)}&=&\displaystyle {\lim _{x\to p}f(x)^{\lim _{x\to p}g(x)}}\end{array}}

Эти правила также действительны для односторонних пределов, в том числе когда $p$ равно ∞ или −∞. В каждом приведенном выше правиле, когда один из пределов справа равен ∞ или −∞, предел слева иногда все еще может определяться следующими правилами.

{\begin{array}{rcl}q+\infty &=&\infty {\text{ if }}q\neq -\infty \\[8pt]q\times \infty &=&{\begin{cases}\infty &{\text{if }}q>0\\-\infty &{\text{if }}q<0\end{cases}}\\[6pt]\displaystyle {\frac {q}{\infty }}&=&0{\text{ if }}q\neq \infty {\text{ and }}q\neq -\infty \\[6pt]\infty ^{q}&=&{\begin{cases}0&{\text{if }}q<0\\\infty &{\text{if }}q>0\end{cases}}\\[4pt]q^{\infty }&=&{\begin{cases}0&{\text{if }}0<q<1\\\infty &{\text{if }}q>1\end{cases}}\\[4pt]q^{-\infty }&=&{\begin{cases}\infty &{\text{if }}0<q<1\\0&{\text{if }}q>1\end{cases}}\end{array}}

(см. также Расширенная строка действительных чисел ).

В других случаях предел слева еще может существовать, хотя правая часть, называемая неопределенной формой , не позволяет определить результат. Это зависит от функций $f$ и $g$ . К неопределенным формам относятся:

{\begin{array}{cc}\displaystyle {\frac {0}{0}}&\displaystyle {\frac {\pm \infty }{\pm \infty }}\\[6pt]0\times \pm \infty &\infty +-\infty \\[8pt]\qquad 0^{0}\qquad &\qquad \infty ^{0}\qquad \\[8pt]1^{\pm \infty }\end{array}}

См. далее правило Лопиталя ниже и неопределенную форму .

Пределы композиций функций [ править ]

В общем, от знания этого $\lim _{y\to b}f(y)=c$ и $\lim _{x\to a}g(x)=b,$ из этого не следует, что $\lim _{x\to a}f(g(x))=c.$ Однако это «цепное правило» действует, если одно из следующих дополнительных выполняется условий:

$f (b) = c$ (то есть $f$ непрерывен в точке $b$ ), или
$g$ не принимает значение $b$ вблизи $a$ (то есть существует $δ > 0$ такое, что если $0 < | x - a | < δ$ , то $| g (x) - b | > 0$ ).

В качестве примера этого явления рассмотрим следующую функцию, которая нарушает оба дополнительных ограничения:

f(x)=g(x)={\begin{cases}0&{\text{if }}x\neq 0\\1&{\text{if }}x=0\end{cases}}

Поскольку значение в точке $f (0)$ является устранимым разрывом ,

\lim _{x\to a}f(x)=0

для всех

а

. Таким образом, правило наивной цепочки предполагает, что предел

f (f (x))

равен 0. Однако это тот случай, когда

f(f(x))={\begin{cases}1&{\text{if }}x\neq 0\\0&{\text{if }}x=0\end{cases}}

и так

\lim _{x\to a}f(f(x))=1

для всех

а

.

Пределы особого интереса [ править ]

Рациональные функции [ править ]

Для $n$ неотрицательное целое число и константы $a_{1},a_{2},a_{3},\ldots ,a_{n}$ и $b_{1},b_{2},b_{3},\ldots ,b_{n},$

\lim _{x\to \infty }{\frac {a_{1}x^{n}+a_{2}x^{n-1}+a_{3}x^{n-2}+\dots +a_{n}}{b_{1}x^{n}+b_{2}x^{n-1}+b_{3}x^{n-2}+\dots +b_{n}}}={\frac {a_{1}}{b_{1}}}

Это можно доказать, разделив числитель и знаменатель на $x. н$ . Если числитель представляет собой многочлен более высокой степени, предела не существует. Если знаменатель имеет более высокую степень, предел равен 0.

Тригонометрические функции [ править ]

{\begin{array}{lcl}\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}&=&1\\[4pt]\displaystyle \lim _{x\to 0}{\frac {1-\cos x}{x}}&=&0\end{array}}

Экспоненциальные функции [ править ]

{\begin{array}{lcl}\displaystyle \lim _{x\to 0}(1+x)^{\frac {1}{x}}&=&\displaystyle \lim _{r\to \infty }\left(1+{\frac {1}{r}}\right)^{r}=e\\[4pt]\displaystyle \lim _{x\to 0}{\frac {e^{x}-1}{x}}&=&1\\[4pt]\displaystyle \lim _{x\to 0}{\frac {e^{ax}-1}{bx}}&=&\displaystyle {\frac {a}{b}}\\[4pt]\displaystyle \lim _{x\to 0}{\frac {c^{ax}-1}{bx}}&=&\displaystyle {\frac {a}{b}}\ln c\\[4pt]\displaystyle \lim _{x\to 0^{+}}x^{x}&=&1\end{array}}

Логарифмические функции [ править ]

{\begin{array}{lcl}\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}&=&1\\[4pt]\displaystyle \lim _{x\to 0}{\frac {\ln(1+ax)}{bx}}&=&\displaystyle {\frac {a}{b}}\\[4pt]\displaystyle \lim _{x\to 0}{\frac {\log _{c}(1+ax)}{bx}}&=&\displaystyle {\frac {a}{b\ln c}}\end{array}}

Правило Лопиталя [ править ]

Это правило использует производные для нахождения пределов неопределенных форм $0/0$ или $\pm\infty/\infty$ и применяется только к таким случаям. В эту форму можно манипулировать и другими неопределенными формами. Учитывая две функции $f (x)$ и $g (x)$ , определенные на открытом интервале $I$ , содержащем желаемую предельную точку $c$ , тогда если:

$\lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0,$ или $\lim _{x\to c}f(x)=\pm \lim _{x\to c}g(x)=\pm \infty ,$ и
$f$ и $g$ дифференцируемы по $I\setminus \{c\},$ и
$g'(x)\neq 0$ для всех $x\in I\setminus \{c\},$ и
$\lim _{x\to c}{\tfrac {f'(x)}{g'(x)}}$ существует,

затем:

\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}.

Обычно первое условие является наиболее важным.

Например: $\lim _{x\to 0}{\frac {\sin(2x)}{\sin(3x)}}=\lim _{x\to 0}{\frac {2\cos(2x)}{3\cos(3x)}}={\frac {2\cdot 1}{3\cdot 1}}={\frac {2}{3}}.$

Суммы и интегралы [ править ]

Указание бесконечной границы суммирования или интеграла является общепринятым сокращением для указания предела.

Короткий способ написать предел $\lim _{n\to \infty }\sum _{i=s}^{n}f(i)$ является $\sum _{i=s}^{\infty }f(i).$ Важным примером пределов таких сумм являются ряды .

Короткий способ написать предел $\lim _{x\to \infty }\int _{a}^{x}f(t)\;dt$ является $\int _{a}^{\infty }f(t)\;dt.$

Короткий способ написать предел $\lim _{x\to -\infty }\int _{x}^{b}f(t)\;dt$ является $\int _{-\infty }^{b}f(t)\;dt.$

См. также [ править ]

Обозначение Big O — описывает предельное поведение функции.
Правило Лопиталя - математическое правило для оценки некоторых пределов.
Список лимитов
Предел последовательности - значение, к которому стремится бесконечная последовательность.
Предельная точка — точка кластера в топологическом пространстве.
Ограничить верхний и нижний предел — границы последовательности.
Сеть (математика) - обобщение последовательности точек.
Нестандартное исчисление – современное применение бесконечно малых.
Теорема о сжатии - метод поиска пределов в исчислении
Последующий предел - предел некоторой подпоследовательности.

Примечания [ править ]

^ Фельшер, Уолтер (2000), «Больцано, Коши, Эпсилон, Дельта», American Mathematical Monthly , 107 (9): 844–862, doi : 10.2307/2695743 , JSTOR 2695743
^ Перейти обратно: ^а ^б Грабинер, Джудит В. (1983), «Кто дал вам эпсилон? Коши и истоки строгого исчисления», American Mathematical Monthly , 90 (3): 185–194, doi : 10.2307/2975545 , JSTOR 2975545 , собрано в Who Дал тебе Эпсилон? , ISBN 978-0-88385-569-0 стр. 5–13. Также доступно по адресу: http://www.maa.org/pubs/Calc_articles/ma002.pdf.
^ Синкевич, Г.И. (2017), «История эпсилонтиков», Antiquitates of Mathematics , 10 , Корнельский университет, arXiv : 1502.06942 , doi : 10.14708/am.v10i0.805
^ Бертон, Дэвид М. (1997), История математики: введение (Третье изд.), Нью-Йорк: McGraw – Hill, стр. 558–559, ISBN. 978-0-07-009465-9
^ Миллер, Джефф (1 декабря 2004 г.), « Самое раннее использование символов исчисления» , получено 18 декабря 2008 г.
^ Перейти обратно: ^а ^б Своковски, Эрл В. (1979), Исчисление с аналитической геометрией (2-е изд.), Тейлор и Фрэнсис, с. 58, ISBN 978-0-87150-268-1
^ Своковски (1979) , с. 72–73.
^ ( Бартл и Шерберт 2000 )
^ Перейти обратно: ^а ^б Бартл (1967)
^ Хаббард (2015)
^ Например, Апостол (1974) , Курант (1924) , Харди (1921) , Рудин (1964) , Уиттакер и Уотсон (1904) все считают «предел» означающим удаленный предел.
^ Например, предел в математической энциклопедии.
^ Стюарт, Джеймс (2020), «Глава 14.2 Пределы и непрерывность», Многомерное исчисление (9-е изд.), Cengage Learning, стр. 952, ISBN 9780357042922
^ Стюарт (2020) , с. 953.
^ Перейти обратно: ^а ^б ^с Закон, Элиас (2011), «Глава 4. Пределы функций и непрерывность», Математический анализ, Том I , Виндзорский университет, стр. 219–220, ISBN 9781617386473
^ Перейти обратно: ^а ^б Закон (2011) , стр. 220.
^ Закон (2011) , стр. 223.
^ Тейлор, Ангус Э. (2012), Общая теория функций и интегрирование , серия Dover Books on Mathematics, стр. 139–140, ISBN 9780486152141
^ Рудин, В. (1986), Принципы математического анализа , Книга C МакГроу-Хилла, стр. 84, ОСЛК 962920758
^ Перейти обратно: ^а ^б Хартман, Грегори (2019), Исчисление векторнозначных функций II , получено 31 октября 2022 г.
^ Закон (2011) , стр. 172.
^ Рудин, В. (1986), Принципы математического анализа , McGraw - Hill Book C, стр. 150–151, OCLC 962920758
^ Кейслер, Х. Джером (2008), «Кванторы в пределах» (PDF) , Анджей Мостовский и фундаментальные исследования , IOS, Амстердам, стр. 151–170.
^ Хрбачек, К. (2007), «Стратифицированный анализ?», Ван Ден Берг, И.; Невес, В. (ред.), Сила нестандартного анализа , Springer.
^ Баащик, Петр; Кац, Михаил ; Шерри, Дэвид (2012), «Десять заблуждений из истории анализа и их разоблачение», Foundations of Science , 18 (1): 43–74, arXiv : 1202.4153 , doi : 10.1007/s10699-012-9285-8 , S2CID 119134151
^ Ф. Рис (7 апреля 1908 г.), «Stetigkeitsbegriff und abstrakte Mengenlehre (Понятие непрерывности и абстрактная теория множеств)», Международный конгресс математиков 1908 г.
^ Своковски (1979) , с. 73.

Ссылки [ править ]

Апостол, Том М. (1974). Математический анализ (2-е изд.). Аддисон-Уэсли. ISBN 0-201-00288-4 .
Бартл, Роберт (1967). Элементы настоящего анализа . Уайли.
Бартл, Роберт Г.; Шерберт, Дональд Р. (2000). Введение в реальный анализ . Уайли.
Курант, Ришар (1924). Лекции по дифференциальному и интегральному исчислению (на немецком языке). Спрингер.
Харди, GH (1921). Курс чистой математики . Издательство Кембриджского университета.
Хаббард, Джон Х. (2015). Векторное исчисление, линейная алгебра и дифференциальные формы: единый подход (5-е изд.). Матричные издания.
Пейдж, Уоррен; Херш, Рубен; Селден, Энни; и др., ред. (2002). «Актуальные новости СМИ». Математический колледж . 33 (2): 147–154. JSTOR 2687124 . .
Рудин, Вальтер (1964). Принципы математического анализа . МакГроу-Хилл.
Сазерленд, Вашингтон (1975). Введение в метрические и топологические пространства . Оксфорд: Издательство Оксфордского университета. ISBN 0-19-853161-3 .
Уиттакер ; Уотсон (1904). Курс современного анализа . Издательство Кембриджского университета.

Внешние ссылки [ править ]

MacTutor История Вейерштрасса.
MacTutor История Больцано
Визуальное исчисление Лоуренса С. Хаша, Университет Теннесси (2001).

[1] Фельшер, Уолтер (2000), «Больцано, Коши, Эпсилон, Дельта», American Mathematical Monthly , 107 (9): 844–862, doi : 10.2307/2695743 , JSTOR 2695743

[Grabiner1983-2] Перейти обратно: ^а ^б Грабинер, Джудит В. (1983), «Кто дал вам эпсилон? Коши и истоки строгого исчисления», American Mathematical Monthly , 90 (3): 185–194, doi : 10.2307/2975545 , JSTOR 2975545 , собрано в Who Дал тебе Эпсилон? , ISBN 978-0-88385-569-0 стр. 5–13. Также доступно по адресу: http://www.maa.org/pubs/Calc_articles/ma002.pdf.

[3] Синкевич, Г.И. (2017), «История эпсилонтиков», Antiquitates of Mathematics , 10 , Корнельский университет, arXiv : 1502.06942 , doi : 10.14708/am.v10i0.805

[4] Бертон, Дэвид М. (1997), История математики: введение (Третье изд.), Нью-Йорк: McGraw – Hill, стр. 558–559, ISBN. 978-0-07-009465-9

[5] Миллер, Джефф (1 декабря 2004 г.), « Самое раннее использование символов исчисления» , получено 18 декабря 2008 г.

[swokowski-6] Перейти обратно: ^а ^б Своковски, Эрл В. (1979), Исчисление с аналитической геометрией (2-е изд.), Тейлор и Фрэнсис, с. 58, ISBN 978-0-87150-268-1

[FOOTNOTESwokowski197972–73-7] Своковски (1979) , с. 72–73.

[8] ( Бартл и Шерберт 2000 )

[Bartle_1967-9] Перейти обратно: ^а ^б Бартл (1967)

[10] Хаббард (2015)

[11] Например, Апостол (1974) , Курант (1924) , Харди (1921) , Рудин (1964) , Уиттакер и Уотсон (1904) все считают «предел» означающим удаленный предел.

[12] Например, предел в математической энциклопедии.

[13] Стюарт, Джеймс (2020), «Глава 14.2 Пределы и непрерывность», Многомерное исчисление (9-е изд.), Cengage Learning, стр. 952, ISBN 9780357042922

[FOOTNOTEStewart2020953-14] Стюарт (2020) , с. 953.

[Zakon_219-15] Перейти обратно: ^а ^б ^с Закон, Элиас (2011), «Глава 4. Пределы функций и непрерывность», Математический анализ, Том I , Виндзорский университет, стр. 219–220, ISBN 9781617386473

[FOOTNOTEZakon2011220-16] Перейти обратно: ^а ^б Закон (2011) , стр. 220.

[FOOTNOTEZakon2011223-17] Закон (2011) , стр. 223.

[18] Тейлор, Ангус Э. (2012), Общая теория функций и интегрирование , серия Dover Books on Mathematics, стр. 139–140, ISBN 9780486152141

[19] Рудин, В. (1986), Принципы математического анализа , Книга C МакГроу-Хилла, стр. 84, ОСЛК 962920758

[Hartman-20] Перейти обратно: ^а ^б Хартман, Грегори (2019), Исчисление векторнозначных функций II , получено 31 октября 2022 г.

[FOOTNOTEZakon2011172-21] Закон (2011) , стр. 172.

[22] Рудин, В. (1986), Принципы математического анализа , McGraw - Hill Book C, стр. 150–151, OCLC 962920758

[23] Кейслер, Х. Джером (2008), «Кванторы в пределах» (PDF) , Анджей Мостовский и фундаментальные исследования , IOS, Амстердам, стр. 151–170.

[24] Хрбачек, К. (2007), «Стратифицированный анализ?», Ван Ден Берг, И.; Невес, В. (ред.), Сила нестандартного анализа , Springer.

[25] Баащик, Петр; Кац, Михаил ; Шерри, Дэвид (2012), «Десять заблуждений из истории анализа и их разоблачение», Foundations of Science , 18 (1): 43–74, arXiv : 1202.4153 , doi : 10.1007/s10699-012-9285-8 , S2CID 119134151

[26] Ф. Рис (7 апреля 1908 г.), «Stetigkeitsbegriff und abstrakte Mengenlehre (Понятие непрерывности и абстрактная теория множеств)», Международный конгресс математиков 1908 г.

[FOOTNOTESwokowski197973-27] Своковски (1979) , с. 73.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

История [ править ]

Мотивация [ править ]

Функции одной переменной [ править ]

( e , d ) - определение предела [ редактировать ]

Существование и односторонние ограничения [ править ]

Более общее определение с использованием предельных точек и подмножеств [ править ]

Удаленные и неудаленные лимиты [ править ]

Примеры [ править ]

Отсутствие одностороннего лимита(ов) [ править ]

Неравенство односторонних пределов [ править ]

Ограничения только в одной точке [ править ]

Пределы в счетном числе точек [ править ]

Пределы, связанные с бесконечностью

Пределы на бесконечности [ править ]

Бесконечные пределы [ править ]

Альтернативное обозначение [ править ]

для рациональных функций Пределы на бесконечности

Функции более чем одной переменной [ править ]

Обычные ограничения [ править ]

Множественные ограничения [ править ]

Множественные ограничения на бесконечности [ править ]

Поточечные пределы и равномерные пределы [ править ]

Итерированные пределы [ править ]

Функции в метрических пространствах [ править ]

Евклидова метрика [ править ]

Манхэттенская метрика [ править ]

Единая метрика [ править ]

Функции в топологических пространствах [ править ]

Другие характеристики [ править ]

С точки зрения последовательностей [ править ]

В нестандартном расчете [ править ]

С точки зрения близости [ править ]

Отношение преемственности к ​

Свойства [ править ]

Пределы композиций функций [ править ]

Пределы особого интереса [ править ]

Рациональные функции [ править ]

Тригонометрические функции [ править ]

Экспоненциальные функции [ править ]

Логарифмические функции [ править ]

Правило Лопиталя [ править ]

Суммы и интегралы [ править ]

См. также [ править ]

Примечания [ править ]

Ссылки [ править ]

Внешние ссылки [ править ]

$(e, d)$ - определение предела [ редактировать ]

Отношение преемственности к