Обобщенная теорема Стокса

Эта статья об обобщенной теореме. Для классической теоремы см. теорему Стокса . Чтобы узнать об уравнении вязкого сопротивления в жидкостях, см. закон Стокса .

В векторном исчислении и дифференциальной геометрии обобщенная теорема Стокса (иногда с апострофом в виде теоремы Стокса или теоремы Стокса ), также называемая теоремой Стокса-Картана , Это утверждение об интегрировании дифференциальных форм на многообразиях , которое одновременно упрощает и обобщает некоторые теоремы векторного исчисления . В частности, фундаментальная теорема исчисления — это частный случай, когда многообразие представляет собой отрезок прямой , теорема Грина и теорема Стокса — это случаи поверхности в $\mathbb {R} ^{2}$ или $\mathbb {R} ^{3},$ а теорема о дивергенции относится к случаю объема в $\mathbb {R} ^{3}.$ Следовательно, эту теорему иногда называют Фундаментальной теоремой многомерного исчисления .

Теорема Стокса гласит, что интеграл дифференциальной формы $\omega$ за границей $\partial \Omega$ некоторого ориентируемого многообразия $\Omega$ равен интегралу от своей внешней производной $d\omega$ на протяжении всего $\Omega$, то есть,

$$\int _{\partial \Omega }\omega =\int _{\Omega }d\omega \,.$$

Теорема Стокса была сформулирована в современной форме Эли Картаном в 1945 году: после более ранних работ по обобщению теорем векторного исчисления Вито Вольтерры , Эдуарда Гурса и Анри Пуанкаре .

Эта современная форма теоремы Стокса представляет собой обширное обобщение классического результата , который лорд Кельвин сообщил Джорджу Стоксу в письме от 2 июля 1850 года. Стоукс задал эту теорему в качестве вопроса на экзамене на премию Смита в 1854 году , в результате чего результат был назван его именем. Впервые оно было опубликовано Германом Ханкелем в 1861 году. классический случай связывает поверхностный интеграл ротора поля векторного Этот ${\textbf {F}}$ (т.е. поток по поверхности ${\text{curl}}\,{\textbf {F}}$) в евклидовом трехмерном пространстве к линейному интегралу векторного поля по границе поверхности.

Введение

Вторая фундаментальная теорема исчисления гласит, что интеграл от функции $f$ за интервал $[a,b]$ можно вычислить, найдя первообразную $F$ из $f$:

$$\int _{a}^{b}f(x)\,dx=F(b)-F(a)\,.$$

Теорема Стокса является обширным обобщением этой теоремы в следующем смысле.

• По выбору $F$, ${\frac {dF}{dx}}=f(x)$. На языке дифференциальных форм это означает, что $f(x)\,dx$ — внешняя производная 0-формы, т. е. функция, $F$: другими словами, это $dF=f\,dx$. Общая теорема Стокса применима к более высокой степени. дифференциальным формам $\omega$ вместо просто 0-форм, таких как $F$.
• Закрытый интервал $[a,b]$является простым примером одномерного многообразия с краем . Его границей является множество, состоящее из двух точек $a$ и $b$. Интеграция $f$на интервале может быть обобщено до интегрирования форм на многомерном многообразии. Необходимы два технических условия: многообразие должно быть ориентируемым , а форма должна иметь компактный носитель , чтобы давать четко определенный интеграл.
• Две точки $a$ и $b$образуют границу замкнутого интервала. В более общем смысле теорема Стокса применима к ориентированным многообразиям. $M$с границей. Граница $\partial M$ из $M$ само является многообразием и наследует естественную ориентацию от ориентации $M$. Например, естественная ориентация интервала дает ориентацию двух граничных точек. Интуитивно, $a$ наследует противоположную ориентацию, поскольку $b$, поскольку они находятся на противоположных концах интервала. Итак, «интеграция» $F$ над двумя граничными точками $a$, $b$ берет на себя разницу $F(b)-F(a)$.

Еще проще, точки можно рассматривать как границы кривых, то есть как 0-мерные границы 1-мерных многообразий. Итак, так же, как можно найти значение интеграла ( $f\,dx=dF$) над одномерным многообразием ( $[a,b]$), рассматривая первообразную ( $F$) на 0-мерных границах ( $\{a,b\}$), можно обобщить фундаментальную теорему исчисления с несколькими дополнительными оговорками, чтобы иметь дело со значением интегралов ( $d\omega$) над $n$-мерные многообразия ( $\Omega$), рассматривая первообразную ( $\omega$) в $(n-1)$-мерные границы ( $\partial \Omega$) многообразия.

Итак, основная теорема гласит:

$$\int _{[a,b]}f(x)\,dx=\int _{[a,b]}\,dF=\int _{\partial [a,b]}\,F=\int _{\{a\}^{-}\cup \{b\}^{+}}F=F(b)-F(a)\,.$$

Формулировка для гладких многообразий с краем

Позволять $\Omega$ — ориентированное гладкое размерности многообразие $n$ с границей и пусть $\alpha$ быть гладким $n$- дифференциальная форма опирающаяся , компактно на $\Omega$. Во-первых, предположим, что $\alpha$ компактно поддерживается в области одной ориентированной координатной карты $\{U,\varphi \}$. В этом случае мы определяем интеграл от $\alpha$ над $\Omega$ как

$$\int _{\Omega }\alpha =\int _{\varphi (U)}(\varphi ^{-1})^{*}\alpha \,,$$

то есть откат через $\alpha$ к $\mathbb {R} ^{n}$.

В более общем смысле интеграл $\alpha$ над $\Omega$ определяется следующим образом: Пусть $\{\psi _{i}\}$ — разбиение единицы , связанное с локально конечным покрытием $\{U_{i},\varphi _{i}\}$ (последовательно ориентированных) координатных карт, затем определите интеграл

$$\int _{\Omega }\alpha \equiv \sum _{i}\int _{U_{i}}\psi _{i}\alpha \,,$$

где каждый член суммы оценивается путем возврата к $\mathbb {R} ^{n}$как описано выше. Эта величина четко определена; то есть не зависит ни от выбора координатных карт, ни от разделения единицы.

Обобщенная теорема Стокса гласит:

Теорема   ( Стокса – Картана ) — Пусть $\omega$ быть гладким $(n-1)$- форма с компактной опорой на ориентированную , $n$-мерное многообразие с краем $M$, где $\partial M$ задана индуцированная ориентация. Тогда

$$\int _{M}d\omega =\int _{\partial M}\omega .$$

Здесь $d$— внешняя производная , которая определяется только с использованием структуры многообразия. Правая часть иногда записывается как ${\textstyle \oint _{\partial \Omega }\omega }$ подчеркнуть тот факт, что $(n-1)$-многообразие $\partial \Omega$ не имеет границы. (Этот факт также является следствием теоремы Стокса, поскольку для заданной гладкой $n$-мерное многообразие $\Omega$, двукратное применение теоремы дает ${\textstyle \int _{\partial (\partial \Omega )}\omega =\int _{\Omega }d(d\omega )=0}$ для любого $(n-2)$-форма $\omega$, что означает, что $\partial (\partial \Omega )=\emptyset$.) Правая часть уравнения часто используется для формулирования интегральных законов; тогда левая часть приводит к эквивалентным дифференциальным формулировкам (см. ниже).

Теорема часто используется в ситуациях, когда $\Omega$ является вложенным ориентированным подмногообразием некоторого большего многообразия, часто $\mathbb {R} ^{k}$, на котором форма $\omega$ определено.

Топологические предварительные сведения; интеграция по цепочкам

Пусть M — гладкое многообразие . (Гладкий) сингулярный k -симплекс в M определяется как гладкое отображение стандартного симплекса в R ^к к М. ​ Группа Ck ₍ свободная M , Z ) особых k - цепей на M определяется как абелева группа на множестве особых k симплексов в M. - Эти группы вместе с граничным отображением ∂ определяют цепной комплекс . Соответствующая группа гомологий (соответственно когомологий) изоморфна обычной сингулярной группе гомологий H _k ( M , Z ) (соответственно сингулярных когомологий группе H ^к ( M , Z ) ), определенный с использованием непрерывных, а не гладких симплексов в M .

С другой стороны, дифференциальные формы с внешней производной d в качестве связующего отображения образуют коцепной комплекс, который определяет когомологий де Рама. группы $H_{dR}^{k}(M,\mathbf {R} )$.

Дифференциальные k -формы можно интегрировать по k -симплексу естественным путем, возвращаясь к R ^к . Расширение по линейности позволяет интегрировать по цепочкам. Это дает линейное отображение пространства k -форм в k -ю группу особых коцепей C ^к ( M , Z ) , линейные функционалы на C _k ( M , Z ) . Другими словами, k -форма ω определяет функционал

$$I(\omega )(c)=\oint _{c}\omega .$$

на k -цепях. Теорема Стокса утверждает, что это цепное отображение когомологий де Рама в сингулярные когомологии с действительными коэффициентами; внешняя производная d ведет себя как двойственная к ∂ на формах. Это дает гомоморфизм когомологий де Рама в сингулярные когомологии. На уровне форм это означает:

1. замкнутые формы, т. е. dω = 0 , имеют нулевой интеграл по границам , т. е. по многообразиям, которые можно записать как ∂Σ _c M _c , и
2. точные формы, т. е. ω = dσ , имеют нулевой интеграл по циклам , т. е. если сумма границ равна пустому множеству: ∂Σ _c M _c = ∅ .

Теорема Де Рама показывает, что этот гомоморфизм на самом деле является изоморфизмом . Таким образом, обратное к пунктам 1 и 2 выше справедливо. Другими словами, если { c _i } — циклы, порождающие k -ю группу гомологий, то для любых соответствующих действительных чисел { a _i } существует замкнутая форма ω такая, что

$$\oint _{c_{i}}\omega =a_{i}\,,$$

и эта форма уникальна с точностью до точных форм.

Теорему Стокса о гладких многообразиях можно вывести из теоремы Стокса для цепей в гладких многообразиях, и наоборот. Формально последнее гласит:

Теорема   ( теорема Стокса для цепей ) — Если c — гладкая k -цепь в гладком многообразии M , а ω — гладкая ( k − 1) -форма на M , то

$$\int _{\partial c}\omega =\int _{c}d\omega .$$

Основополагающий принцип

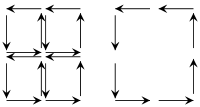
Чтобы упростить эти топологические аргументы, стоит изучить основополагающий принцип, рассмотрев пример для измерений d = 2 . Основную идею можно понять с помощью диаграммы слева, которая показывает, что в ориентированном замощении многообразия внутренние пути проходят в противоположных направлениях; таким образом, их вклады в интеграл по путям попарно компенсируют друг друга. В результате остается только вклад границы. Таким образом, достаточно доказать теорему Стокса для достаточно тонких мозаик (или, что то же самое, симплексов ), что обычно не составляет труда.

анализа

Позволять $\gamma :[a,b]\to \mathbb {R} ^{2}$— кусочно- гладкая плоская жорданова кривая . означает Теорема Жордана о кривой , что $\gamma$ делит $\mathbb {R} ^{2}$на две компоненты: компактную и некомпактную. Позволять $D$ обозначим компактную часть, ограниченную $\gamma$ и предположим $\psi :D\to \mathbb {R} ^{3}$ гладкая, с $S=\psi (D)$. Если $\Gamma$ - пространственная кривая , определяемая формулой $\Gamma (t)=\psi (\gamma (t))$ и ${\textbf {F}}$ представляет собой гладкое векторное поле на $\mathbb {R} ^{3}$, затем:

$$\oint _{\Gamma }\mathbf {F} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\left(\nabla \times \mathbf {F} \right)\cdot \,d\mathbf {S}$$

Это классическое утверждение является частным случаем общей формулировки после отождествления векторного поля с 1-формой, а его ротора с двойной формой через

$${\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\\\end{pmatrix}}\cdot d\Gamma \to F_{x}\,dx+F_{y}\,dy+F_{z}\,dz$$

$${\begin{aligned}&\nabla \times {\begin{pmatrix}F_{x}\\F_{y}\\F_{z}\end{pmatrix}}\cdot d\mathbf {S} ={\begin{pmatrix}\partial _{y}F_{z}-\partial _{z}F_{y}\\\partial _{z}F_{x}-\partial _{x}F_{z}\\\partial _{x}F_{y}-\partial _{y}F_{x}\\\end{pmatrix}}\cdot d\mathbf {S} \to \\[1.4ex]&d(F_{x}\,dx+F_{y}\,dy+F_{z}\,dz)=\left(\partial _{y}F_{z}-\partial _{z}F_{y}\right)dy\wedge dz+\left(\partial _{z}F_{x}-\partial _{x}F_{z}\right)dz\wedge dx+\left(\partial _{x}F_{y}-\partial _{y}F_{x}\right)dx\wedge dy.\end{aligned}}$$

Обобщение на грубые множества

Область (здесь она называется D вместо Ω ) с кусочно-гладкой границей. Это многообразие с углами , поэтому его граница не является гладким многообразием.

Приведенная выше формулировка, в которой $\Omega$является гладким многообразием с краем, во многих приложениях недостаточно. Например, если область интегрирования определяется как плоская область между двумя $x$-координаты и графики двух функций, часто бывает, что область имеет углы. В таком случае угловые точки означают, что $\Omega$не является гладким многообразием с краем, поэтому приведенное выше утверждение теоремы Стокса неприменимо. Тем не менее можно проверить, что заключение теоремы Стокса по-прежнему верно. Это потому что $\Omega$ и его граница хорошо ведут себя вдали от небольшого набора точек ( множества нулевой меры ).

Версия теоремы Стокса, допускающая шероховатость, была доказана Уитни. Предположим, что $D$ является связным ограниченным открытым подмножеством $\mathbb {R} ^{n}$. Вызов $D$ стандартный домен, если он удовлетворяет следующему свойству: существует подмножество $P$ из $\partial D$, открыть в $\partial D$, дополнение которого в $\partial D$ есть Хаусдорф $(n-1)$-измерить ноль; и такой, что каждая точка $P$имеет обобщенный вектор нормали . Это вектор ${\textbf {v}}(x)$ такое, что если система координат выбрана так, что ${\textbf {v}}(x)$ является первым базисным вектором, то в открытой окрестности вокруг $x$, существует гладкая функция $f(x_{2},\dots ,x_{n})$ такой, что $P$ это график $\{x_{1}=f(x_{2},\dots ,x_{n})\}$ и $D$ это регион $\{x_{1}:x_{1}<f(x_{2},\dots ,x_{n})\}$. Уитни отмечает, что граница стандартной области представляет собой объединение множества нулевых Хаусдорфовых $(n-1)$-мера и конечное или счетное объединение гладких $(n-1)$-многообразия, каждое из которых имеет область определения только на одной стороне. Затем он доказывает, что если $D$ это стандартный домен в $\mathbb {R} ^{n}$, $\omega$ является $(n-1)$-форма, определенная, непрерывная и ограниченная на $D\cup P$, плавно $D$, интегрируемый на $P$, и такой, что $d\omega$ интегрируемо на $D$, то справедлива теорема Стокса, т. е.

$$\int _{P}\omega =\int _{D}d\omega \,.$$

Изучение теоретико-мерных свойств грубых множеств приводит к геометрической теории меры . Еще более общие версии теоремы Стокса были доказаны Федерером и Харрисоном.

Особые случаи

Общая форма теоремы Стокса с использованием дифференциальных форм более мощна и проста в использовании, чем частные случаи. Традиционные версии могут быть сформулированы с использованием декартовых координат без применения дифференциальной геометрии и, следовательно, более доступны. Кроме того, они старше, и в результате их имена более знакомы. Традиционные формы часто считаются более удобными для практикующих ученых и инженеров, но неестественность традиционной формулировки становится очевидной при использовании других систем координат, даже таких привычных, как сферические или цилиндрические координаты. Существует вероятность путаницы в применении названий и использовании двойных формулировок.

Классический (векторное

Основная статья: теорема Стокса

Иллюстрация теоремы Стокса о векторном исчислении с поверхностью $\Sigma$, его граница $\partial \Sigma$ и «нормальный» вектор n .

Это (дуализированный) (1 + 1)-мерный случай для 1-формы (дуализированной, поскольку это утверждение о векторных полях ). Этот особый случай во многих вводных университетских курсах векторного исчисления часто называют просто теоремой Стокса и используется в физике и технике. Ее также иногда называют теоремой о роторе .

Классическая теорема Стокса связывает поверхностный интеграл ротора поля векторного по поверхности $\Sigma$в евклидовом трехмерном пространстве к линейному интегралу векторного поля по его границе. Это частный случай общей теоремы Стокса (с $n=2$) как только мы отождествляем векторное поле с 1-формой, используя метрику в евклидовом 3-пространстве. Кривая линейного интеграла, $\partial \Sigma$, должен иметь положительную направленность , то есть $\partial \Sigma$ указывает против часовой стрелки, когда поверхность нормальная , $n$, указывает на зрителя.

Одним из следствий этой теоремы является то, что силовые линии векторного поля с нулевым ротором не могут быть замкнутыми контурами. Формулу можно переписать так:

Теорема . Предположим , ${\textbf {F}}={\big (}P(x,y,z),Q(x,y,z),R(x,y,z){\big )}$ определяется в области с гладкой поверхностью $\Sigma$ первого порядка и имеет непрерывные частные производные . Затем

$$\iint _{\Sigma }{\Biggl (}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)dy\,dz+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)dz\,dx+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)dx\,dy{\Biggr )}=\oint _{\partial \Sigma }{\Big (}P\,dx+Q\,dy+R\,dz{\Big )}\,,$$

где $P,Q$ и $R$ являются компонентами ${\textbf {F}}$, и $\partial \Sigma$ это граница региона $\Sigma$.

Теорема Грина

Теорема Грина сразу узнаваема как третий подынтегральный знак обеих частей интеграла в терминах P , Q и R , упомянутых выше.

В электромагнетизме

Два из четырех уравнений Максвелла включают роторы трехмерных векторных полей, а их дифференциальная и интегральная формы связаны специальным трехмерным (векторным исчислением) случаем теоремы Стокса . Необходимо проявлять осторожность, чтобы избежать случаев с подвижными границами: частные производные по времени предназначены для исключения таких случаев. Если включены движущиеся границы, то замена интегрирования и дифференцирования приводит к появлению членов, связанных с движением границ, не включенных в результаты ниже (см. Дифференцирование под знаком интеграла ):

Имя	Дифференциальная форма	Интегральная форма (с использованием трехмерной теоремы Стокса плюс релятивистская инвариантность, $\textstyle \int {\tfrac {\partial }{\partial t}}\dots \to {\tfrac {d}{dt}}\textstyle \int \cdots$)
Уравнение Максвелла – Фарадея Закон индукции Фарадея :	$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$	${\begin{aligned}\oint _{C}\mathbf {E} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {E} \cdot d\mathbf {A} \\&=-\iint _{S}{\frac {\partial \mathbf {B} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}$ (при этом C и S не обязательно стационарны)
Закон Ампера (с расширением Максвелла):	$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}$	${\begin{aligned}\oint _{C}\mathbf {H} \cdot d\mathbf {l} &=\iint _{S}\nabla \times \mathbf {H} \cdot d\mathbf {A} \\&=\iint _{S}\mathbf {J} \cdot d\mathbf {A} +\iint _{S}{\frac {\partial \mathbf {D} }{\partial t}}\cdot d\mathbf {A} \end{aligned}}$ (при этом C и S не обязательно стационарны)

Перечисленная выше подгруппа уравнений Максвелла справедлива для электромагнитных полей, выраженных в единицах СИ . В других системах единиц, таких как СГС или гауссовы единицы , коэффициенты масштабирования для терминов различаются. Например, в гауссовских единицах закон индукции Фарадея и закон Ампера принимают формы:

$${\begin{aligned}\nabla \times \mathbf {E} &=-{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}\,,\\\nabla \times \mathbf {H} &={\frac {1}{c}}{\frac {\partial \mathbf {D} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {J} \,,\end{aligned}}$$

соответственно, где c — скорость света в вакууме.

Теорема

Аналогично, теорема о расходимости

$$\int _{\mathrm {Vol} }\nabla \cdot \mathbf {F} \,d_{\mathrm {Vol} }=\oint _{\partial \operatorname {Vol} }\mathbf {F} \cdot d{\boldsymbol {\Sigma }}$$

является особым случаем, если мы отождествляем векторное поле с $(n-1)$-форма, полученная сжатием векторного поля с евклидовой формой объема. Применение этого случая ${\textbf {F}}=f{\vec {c}}$ где ${\vec {c}}$— произвольный постоянный вектор. Вычисление расхождения произведения дает

$${\vec {c}}\cdot \int _{\mathrm {Vol} }\nabla f\,d_{\mathrm {Vol} }={\vec {c}}\cdot \oint _{\partial \mathrm {Vol} }f\,d{\boldsymbol {\Sigma }}\,.$$

Поскольку это справедливо для всех ${\vec {c}}$ мы нашли

$$\int _{\mathrm {Vol} }\nabla f\,d_{\mathrm {Vol} }=\oint _{\partial \mathrm {Vol} }f\,d{\boldsymbol {\Sigma }}\,.$$

Объемный интеграл градиента скалярного поля

Позволять $f:\Omega \to \mathbb {R}$быть скалярным полем . Затем

$$\int _{\Omega }{\vec {\nabla }}f=\int _{\partial \Omega }{\vec {n}}f$$

где ${\vec {n}}$ к вектор нормали поверхности $\partial \Omega$ в данный момент.

Доказательство: Позволять ${\vec {c}}$быть вектором. Затем

$${\begin{aligned}0&=\int _{\Omega }{\vec {\nabla }}\cdot {\vec {c}}f-\int _{\partial \Omega }{\vec {n}}\cdot {\vec {c}}f&{\text{by the divergence theorem}}\\&=\int _{\Omega }{\vec {c}}\cdot {\vec {\nabla }}f-\int _{\partial \Omega }{\vec {c}}\cdot {\vec {n}}f\\&={\vec {c}}\cdot \int _{\Omega }{\vec {\nabla }}f-{\vec {c}}\cdot \int _{\partial \Omega }{\vec {n}}f\\&={\vec {c}}\cdot \left(\int _{\Omega }{\vec {\nabla }}f-\int _{\partial \Omega }{\vec {n}}f\right)\end{aligned}}$$

Поскольку это справедливо для любого ${\vec {c}}$ (в частности, для каждого базисного вектора ) результат следующий.

См. также

• Лемма Чандрасекара – Вентцеля

Дальнейшее чтение

• Грунский, Гельмут (1983). Общая теорема Стокса . Бостон: Питман. ISBN  0-273-08510-7 .
• Кац, Виктор Дж. (май 1979 г.). «История теоремы Стокса». Журнал «Математика» . 52 (3): 146–156. дои : 10.2307/2690275 . JSTOR   2690275 .
• Лумис, Линн Гарольд ; Штернберг, Шломо (2014). Продвинутое исчисление . Хакенсак, Нью-Джерси: World Scientific. ISBN  978-981-4583-93-0 .
• Мэдсен, Иб ; Торнехаве, Йорген (1997). От исчисления к когомологиям: когомологии Де Рама и характеристические классы . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-58956-8 .
• Марсден, Джерролд Э .; Энтони, Тромба (2003). Векторное исчисление (5-е изд.). У. Х. Фриман.
• Ли, Джон (2003). Введение в гладкие многообразия . Спрингер-Верлаг. ISBN  978-0-387-95448-6 .
• Рудин, Вальтер (1976). Принципы математического анализа . Нью-Йорк, штат Нью-Йорк: МакГроу – Хилл. ISBN  0-07-054235-Х .
• Спивак, Михаил (1965). Исчисление на многообразиях: современный подход к классическим теоремам расширенного исчисления . Сан-Франциско: Бенджамин Каммингс. ISBN  0-8053-9021-9 .
• Стюарт, Джеймс (2009). Исчисление: концепции и контексты . Cengage Обучение. стр. 960–967. ISBN  978-0-495-55742-5 .
• Стюарт, Джеймс (2003). Исчисление: ранние трансцендентные функции (5-е изд.). Брукс/Коул.
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Нью-Йорк: Спрингер. ISBN  978-1-4419-7399-3 .

Внешние ссылки

• «Формула Стокса» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Доказательство теоремы о расходимости и теоремы Стокса.
• Исчисление 3 – Теорема Стокса от lamar.edu – поясняющее объяснение