Закон индукции Фарадея

Эксперимент Фарадея, демонстрирующий индукцию между катушками провода: Жидкостная батарея (справа) обеспечивает ток, который течет через небольшую катушку ( А ), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка перемещается в большую катушку ( B ) или из нее, магнитный поток через большую катушку изменяется, индуцируя ток, который обнаруживается гальванометром ( G ).

Закон индукции Фарадея (или просто закон Фарадея ) — это закон электромагнетизма , предсказывающий, как магнитное поле будет взаимодействовать с электрической цепью , создавая электродвижущую силу (ЭДС). Это явление, известное как электромагнитная индукция , является фундаментальным принципом работы трансформаторов , индукторов и многих типов электродвигателей , генераторов и соленоидов .

Уравнение Максвелла-Фарадея (включенное в список уравнений Максвелла ) описывает тот факт, что пространственно меняющееся (а также, возможно, изменяющееся во времени, в зависимости от того, как магнитное поле меняется во времени) электрическое поле всегда сопровождает изменяющееся во времени магнитное поле, в то время как Закон Фарадея гласит, что в проводящем контуре возникает ЭДС (электродвижущая сила, определяемая как электромагнитная работа, совершаемая над единицей заряда, когда он проходит один оборот по проводящему контуру), когда магнитный поток проходит через него. поверхность, заключенная в петлю, меняется во времени.

Был открыт закон Фарадея, и один из его аспектов (ЭДС трансформатора) позже был сформулирован как уравнение Максвелла – Фарадея. Уравнение закона Фарадея может быть получено с помощью уравнения Максвелла – Фарадея (описывающего ЭДС трансформатора) и силы Лоренца (описывающей ЭДС движения). Интегральная форма уравнения Максвелла-Фарадея описывает только ЭДС трансформатора, тогда как уравнение закона Фарадея описывает как ЭДС трансформатора, так и ЭДС движения.

История

Электромагнитная индукция была открыта независимо Майклом Фарадеем в 1831 году и Джозефом Генри в 1832 году. Фарадей первым опубликовал результаты своих экспериментов.

Демонстрация Фарадея 1831 года.

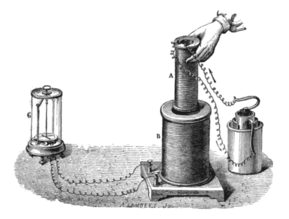
Записная книжка Фарадея 29 августа 1831 года. описывает экспериментальную демонстрацию электромагнитной индукции (см. рисунок). который обматывает два провода вокруг противоположных сторон железного кольца (как современный тороидальный трансформатор ). Его оценка недавно открытых свойств электромагнитов показала, что, когда ток начинает течь по одному проводу, своего рода волна проходит через кольцо и вызывает некоторый электрический эффект на противоположной стороне. Действительно, игла гальванометра измеряла переходный ток (который он назвал «волной электричества») на правом проводе, когда он подключал или отключал левый провод от батареи. Эта индукция происходила из-за изменения магнитного потока , происходящего при подключении и отключении батареи. В его записной книжке также отмечалось, что меньшее количество витков со стороны батареи приводило к большему повреждению стрелки гальванометра.

В течение двух месяцев Фарадей обнаружил еще несколько проявлений электромагнитной индукции. Например, он видел переходные токи, когда быстро вставлял и вынимал стержневой магнит из катушки с проводами, и генерировал постоянный ( постоянный ) ток, вращая медный диск рядом со стержневым магнитом с помощью скользящего электрического вывода (« Диск Фарадея»). ").

Диск Фарадея, первый электрический генератор , разновидность униполярного генератора.

Майкл Фарадей объяснил электромагнитную индукцию, используя концепцию, которую он назвал силовыми линиями . Однако ученые того времени широко отвергли его теоретические идеи, главным образом потому, что они не были сформулированы математически. Исключением был Джеймс Клерк Максвелл , который в 1861–62 использовал идеи Фарадея как основу своей количественной электромагнитной теории. В работах Максвелла изменяющийся во времени аспект электромагнитной индукции выражается в виде дифференциального уравнения, которое Оливер Хевисайд назвал законом Фарадея, хотя оно отличается от исходной версии закона Фарадея и не описывает ЭДС движения . Версия Хевисайда (см. уравнение Максвелла-Фарадея ниже ) представляет собой форму, признанную сегодня в группе уравнений, известных как уравнения Максвелла .

Закон Ленца , сформулированный Эмилем Ленцем в 1834 году: описывает «поток в цепи» и дает направление индуцированной ЭДС и тока, возникающего в результате электромагнитной индукции (подробно описано в примерах ниже).

По словам Альберта Эйнштейна , большая часть основ и открытий его специальной теории относительности была заложена этим законом индукции Фарадея в 1834 году.

Закон Фарадея

Переменный электрический ток протекает через соленоид слева, создавая изменяющееся магнитное поле. Это поле за счет электромагнитной индукции заставляет электрический ток течь в проволочной петле справа.

Самая распространенная версия закона Фарадея гласит:

Электродвижущая сила вокруг замкнутого пути равна отрицательной скорости изменения магнитного потока, заключенного в пути, во времени.

Математическое утверждение

Определение поверхностного интеграла основано на разбиении поверхности Σ на небольшие элементы поверхности. Каждому элементу сопоставлен вектор d A величиной, равной площади элемента, с направлением, нормальным к элементу и направленным «наружу» (относительно ориентации поверхности).

Для витка провода в магнитном поле магнитный поток Φ _B определен для любой поверхности Σ, которой границей является данный виток. Поскольку проволочная петля может двигаться, мы обозначаем Σ( t ) поверхность . Магнитный поток представляет собой поверхностный интеграл : $$\Phi _{B}=\iint _{\Sigma (t)}\mathbf {B} (t)\cdot \mathrm {d} \mathbf {A} \,,$$ где d A — это элемент вектора площади движущейся поверхности Σ( t ) , B — магнитное поле, а B · d A — векторное скалярное произведение представляющее элемент потока через d A. , Говоря более наглядно, магнитный поток через проволочную петлю пропорционален количеству силовых линий магнитного поля , проходящих через петлю.

Когда поток изменяется (из-за изменения B , или из-за того, что проволочная петля перемещается или деформируется, или из-за того и другого), закон индукции Фарадея гласит, что проволочная петля приобретает ЭДС , определяемую как энергию, доступную от единичного заряда, который прошел один раз вокруг проволочная петля. (Хотя в некоторых источниках это определение сформулировано по-другому, это выражение было выбрано для совместимости с уравнениями специальной теории относительности .) Эквивалентно, это напряжение, которое можно было бы измерить, перерезав провод для создания разомкнутой цепи и прикрепив вольтметр. к его выводам .

Закон Фарадея гласит, что ЭДС также определяется скоростью изменения магнитного потока: $${\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}},$$ где ${\mathcal {E}}$ – электродвижущая сила (ЭДС), а Φ _B – магнитный поток .

Направление электродвижущей силы задается законом Ленца .

Законы индукции электрического тока в математической форме были установлены Францем Эрнстом Нейманом в 1845 году.

Закон Фарадея содержит информацию о взаимосвязях между величинами и направлениями его переменных. Однако связи между направлениями не являются явными; они скрыты в математической формуле.

Правило левой руки для закона Фарадея. Знак ΔΦ _B , изменения потока, находится на основе соотношения между магнитным полем B , площадью петли A и нормалью n к этой площади, представленной пальцами левой руки. Если ΔΦ _B положительна, направление ЭДС такое же, как у изогнутых пальцев (желтые стрелки). Если ΔΦ _B отрицательно, то направление ЭДС направлено против стрелок.

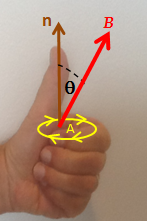
Направление электродвижущей силы (ЭДС) можно узнать непосредственно из закона Фарадея, не прибегая к закону Ленца. В этом помогает правило левой руки:

• Совместите согнутые пальцы левой руки с петлей (желтая линия).
• Вытяните большой палец. Вытянутый большой палец указывает направление n (коричневое), нормали к области, заключенной в петлю.
• Найдите знак ΔΦ _B , изменения потока. Определите начальный и конечный потоки (разница которых равна ΔΦ _B ) относительно нормального n , на что указывает вытянутый большой палец.
• Если изменение потока ΔΦ _B положительное, изогнутые пальцы показывают направление электродвижущей силы (желтые стрелки).
• Если ΔΦ _B отрицательно, направление электродвижущей силы противоположно направлению изогнутых пальцев (противоположно желтым наконечникам стрелок).

Для туго намотанной катушки провода , состоящей из N одинаковых витков, каждый с одинаковым Φ _B , закон индукции Фарадея гласит, что $${\mathcal {E}}=-N{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}$$ где N — количество витков провода, а Φ _B — магнитный поток через один контур.

Уравнение Максвелла – Фарадея

Иллюстрация теоремы Кельвина–Стокса с поверхностью Σ , ее границей ∂ Σ и ориентацией n, заданной правилом правой руки .

Уравнение Максвелла-Фарадея утверждает, что изменяющееся во времени магнитное поле всегда сопровождает пространственно меняющееся (также, возможно, изменяющееся во времени) неконсервативное электрическое поле, и наоборот. Уравнение Максвелла – Фарадея имеет вид

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$

(в единицах СИ ), где ∇ × — ротора оператор , E ( r , t ) — электрическое поле , а B ( r , t ) — магнитное поле . Эти поля обычно могут быть функциями позиции r и времени t .

Уравнение Максвелла-Фарадея является одним из четырёх уравнений Максвелла и поэтому играет фундаментальную роль в теории классического электромагнетизма . Его также можно записать в интегральной форме по теореме Кельвина–Стокса : воспроизводя тем самым закон Фарадея:

$\oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-\int _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot \mathrm {d} \mathbf {A}$

где, как указано на рисунке, Σ — поверхность, ограниченная замкнутым контуром ∂ Σ , d l — бесконечно малый векторный элемент контура ∂Σ , а d A — бесконечно малый векторный элемент поверхности Σ . Его направление ортогонально этому участку поверхности, а величина равна площади бесконечно малого участка поверхности.

И d l, и d A имеют неоднозначность знака; чтобы получить правильный знак, используется правило правой руки , как объяснено в статье Теорема Кельвина – Стокса . Для плоской поверхности Σ положительный элемент пути d l кривой ∂ Σ определяется по правилу правой руки как элемент, который указывает пальцами правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ. .

Линейный интеграл вокруг ∂ Σ называется циркуляцией . Ненулевая циркуляция E отличается от поведения электрического поля, создаваемого статическими зарядами. Генерируемое зарядом E -поле может быть выражено как градиент скалярного поля , которое является решением уравнения Пуассона и имеет нулевой интеграл по пути. См. теорему о градиенте .

Интегральное уравнение верно для любого пути ∂ Σ через пространство и любой поверхности Σ , для которой этот путь является границей.

Если поверхность Σ не меняется во времени, уравнение можно переписать: $$\oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {l} =-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {A} .$$ Поверхностный интеграл в правой части является явным выражением магнитного потока Φ _B через Σ .

Электрическое векторное поле, индуцированное изменяющимся магнитным потоком, соленоидальная составляющая общего электрического поля, может быть аппроксимировано в нерелятивистском пределе объемным интегральным уравнением $$\mathbf {E} _{s}(\mathbf {r} ,t)\approx -{\frac {1}{4\pi }}\iiint _{V}\ {\frac {\left({\frac {\partial \mathbf {B} (\mathbf {r} ',t)}{\partial t}}\right)\times \left(\mathbf {r} -\mathbf {r} '\right)}{|\mathbf {r} -\mathbf {r} '|^{3}}}d^{3}\mathbf {r'}$$

Доказательство

Четыре уравнения Максвелла (включая уравнение Максвелла-Фарадея), а также закон силы Лоренца, являются достаточной основой для вывода всего , что связано с классическим электромагнетизмом . Следовательно, можно «доказать» закон Фарадея, исходя из этих уравнений.

Отправной точкой является производная по времени потока через произвольную поверхность Σ (которую можно перемещать или деформировать) в пространстве: $${\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma (t)}\mathbf {B} (t)\cdot \mathrm {d} \mathbf {A}$$

(по определению). Эту полную производную по времени можно оценить и упростить с помощью уравнения Максвелла – Фарадея и некоторых векторных тождеств; подробности в поле ниже:

Рассмотрим производную по времени магнитного потока через замкнутую границу (петлю), которая может перемещаться или деформироваться. Площадь, ограниченную петлей, обозначается как Σ( t ) ), тогда производную по времени можно выразить как $${\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma (t)}\mathbf {B} (t)\cdot \mathrm {d} \mathbf {A}$$ Интеграл может меняться со временем по двум причинам: может меняться подынтегральная функция или может меняться область интегрирования. Они складываются линейно, поэтому: $$\left.{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}\right|_{t=t_{0}}=\left(\int _{\Sigma (t_{0})}\left.{\frac {\partial \mathbf {B} }{\partial t}}\right|_{t=t_{0}}\cdot \mathrm {d} \mathbf {A} \right)+\left({\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot \mathrm {d} \mathbf {A} \right)$$ где t 0 - любое заданное фиксированное время. Покажем, что первое слагаемое в правой части соответствует ЭДС трансформатора, второе — ЭДС движения (от магнитной силы Лоренца на носителях заряда, обусловленной движением или деформацией проводящего контура в магнитном поле). Первое слагаемое в правой части можно переписать, используя интегральную форму уравнения Максвелла – Фарадея: $$\int _{\Sigma (t_{0})}\left.{\frac {\partial \mathbf {B} }{\partial t}}\right|_{t=t_{0}}\cdot \mathrm {d} \mathbf {A} =-\oint _{\partial \Sigma (t_{0})}\mathbf {E} (t_{0})\cdot \mathrm {d} \mathbf {l}$$ Далее анализируем второе слагаемое в правой части: 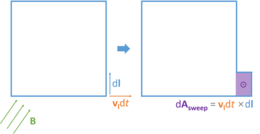$${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot \mathrm {d} \mathbf {A}$$ Площадь, охваченная векторным элементом d l петли ∂ Σ за время d t при его движении со скоростью v l . Доказательство этого несколько сложнее, чем первое слагаемое; более подробную информацию и альтернативные подходы к доказательству можно найти в ссылках. Когда петля движется и/или деформируется, она сметает поверхность (см. рисунок справа). Поскольку небольшая часть петли d l движется со скоростью v l за короткое время d t , она выметает область, вектор которой равен d A развертка = v l d t × d l (обратите внимание, что этот вектор направлен наружу от изображение на правом рисунке). Следовательно, изменение магнитного потока через контур вследствие деформации или перемещения контура за время d t равно $$\mathrm {d} \Phi _{B}=\int \mathbf {B} \cdot \mathrm {d} \mathbf {A} _{\text{sweep}}=\int \mathbf {B} \cdot (\mathbf {v} _{\mathbf {l} }\mathrm {d} t\times \mathrm {d} \mathbf {l} )=-\int \mathrm {d} t\,\mathrm {d} \mathbf {l} \cdot (\mathbf {v} _{\mathbf {l} }\times \mathbf {B} )$$ Здесь тождества тройных скалярных произведений используются . Поэтому, $${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma (t)}\mathbf {B} (t_{0})\cdot \mathrm {d} \mathbf {A} =-\oint _{\partial \Sigma (t_{0})}(\mathbf {v} _{\mathbf {l} }(t_{0})\times \mathbf {B} (t_{0}))\cdot \mathrm {d} \mathbf {l}$$ где v l — скорость части петли ∂ Σ . Если сложить все это вместе, получится: $$\left.{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}\right|_{t=t_{0}}=\left(-\oint _{\partial \Sigma (t_{0})}\mathbf {E} (t_{0})\cdot \mathrm {d} \mathbf {l} \right)+\left(-\oint _{\partial \Sigma (t_{0})}{\bigl (}\mathbf {v} _{\mathbf {l} }(t_{0})\times \mathbf {B} (t_{0}){\bigr )}\cdot \mathrm {d} \mathbf {l} \right)$$ $$\left.{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}\right|_{t=t_{0}}=-\oint _{\partial \Sigma (t_{0})}{\bigl (}\mathbf {E} (t_{0})+\mathbf {v} _{\mathbf {l} }(t_{0})\times \mathbf {B} (t_{0}){\bigr )}\cdot \mathrm {d} \mathbf {l} .$$

Результат: $${\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}=-\oint _{\partial \Sigma }\left(\mathbf {E} +\mathbf {v} _{\mathbf {l} }\times \mathbf {B} \right)\cdot \mathrm {d} \mathbf {l} .$$ где ∂Σ — граница (петля) поверхности Σ , а v _l — скорость части границы.

В случае проводящего контура ЭДС (электродвижущая сила) — это электромагнитная работа, совершаемая над единицей заряда, когда он проходит вокруг контура один раз, и эта работа выполняется силой Лоренца . Следовательно, ЭДС выражается как $${\mathcal {E}}=\oint \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot \mathrm {d} \mathbf {l}$$ где ${\mathcal {E}}$ — ЭДС, а v — скорость единичного заряда.

С макроскопической точки зрения для зарядов на участке петли v состоит в среднем из двух компонентов; одна — скорость заряда на отрезке , _vt другая — скорость отрезка vl _. (петля деформирована или сдвинута) v _t не вносит вклад в работу, совершаемую над зарядом, поскольку направление v _t совпадает с направлением $\mathrm {d} \mathbf {l}$. Математически, $$(\mathbf {v} \times \mathbf {B} )\cdot \mathrm {d} \mathbf {l} =((\mathbf {v} _{t}+\mathbf {v} _{l})\times \mathbf {B} )\cdot \mathrm {d} \mathbf {l} =(\mathbf {v} _{t}\times \mathbf {B} +\mathbf {v} _{l}\times \mathbf {B} )\cdot \mathrm {d} \mathbf {l} =(\mathbf {v} _{l}\times \mathbf {B} )\cdot \mathrm {d} \mathbf {l}$$ с $(\mathbf {v} _{t}\times \mathbf {B} )$ перпендикулярен $\mathrm {d} \mathbf {l}$ как $\mathbf {v} _{t}$ и $\mathrm {d} \mathbf {l}$ находятся в одном направлении. Теперь мы видим, что для проводящей петли ЭДС такая же, как производная по времени магнитного потока через петлю, за исключением знака. Таким образом, теперь мы приходим к уравнению закона Фарадея (для проводящей петли) как $${\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}=-{\mathcal {E}}$$ где ${\textstyle {\mathcal {E}}=\oint \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)\cdot \mathrm {d} \mathbf {l} }$. Нарушая этот интеграл, ${\textstyle \oint \mathbf {E} \cdot \mathrm {d} \mathbf {l} }$ для ЭДС трансформатора (из-за изменяющегося во времени магнитного поля) и ${\textstyle \oint \left(\mathbf {v} \times \mathbf {B} \right)\cdot \mathrm {d} \mathbf {l} =\oint \left(\mathbf {v} _{l}\times \mathbf {B} \right)\cdot \mathrm {d} \mathbf {l} }$ для ЭДС движения (из-за магнитной силы Лоренца, действующей на заряды при движении или деформации петли в магнитном поле).

Исключения

Смотрите также: парадокс Фарадея

См. также: Парадокс Геринга.

Соблазнительно обобщить закон Фарадея и заявить: если ∂Σ — это любой произвольный замкнутый контур в пространстве, то полная производная по времени магнитного потока через Σ равна ЭДС вокруг ∂Σ . Это утверждение, однако, не всегда верно, и причина не только в том, что ЭДС не определена в пустом пространстве, когда проводник отсутствует. Как отмечалось в предыдущем разделе, работа закона Фарадея не гарантируется, если скорость абстрактной кривой ∂Σ не соответствует фактической скорости материала, проводящего электричество. Два примера, проиллюстрированные ниже, показывают, что часто получают неправильные результаты, когда движение ∂Σ отделено от движения материала.

• 
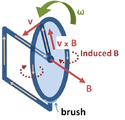
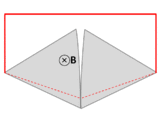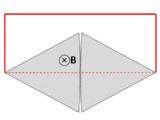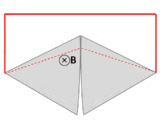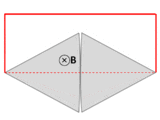
  Фарадея Униполярный генератор . Диск вращается с угловой скоростью ω , охватывая проводящий радиус по кругу в статическом магнитном поле B (направление вдоль нормали к поверхности диска). Магнитная сила Лоренца v × B пропускает ток по проводящему радиусу к проводящему ободу, и оттуда цепь замыкается через нижнюю щетку и ось, поддерживающую диск. Это устройство генерирует ЭДС и ток, хотя форма «цепи» постоянна и, следовательно, поток через цепь не меняется со временем.
• 
  Провод (сплошные красные линии) соединяется с двумя соприкасающимися металлическими пластинами (серебряными), образуя цепь. Вся система находится в однородном магнитном поле, перпендикулярном странице. Если абстрактный путь ∂Σ следует основному пути прохождения тока (отмечен красным), то магнитный поток по этому пути резко меняется при вращении пластин, но ЭДС почти равна нулю. После Фейнмановских лекций по физике

Подобные примеры можно проанализировать, позаботившись о том, чтобы путь ∂Σ двигался с той же скоростью, что и материал. Альтернативно, всегда можно правильно рассчитать ЭДС, объединив закон силы Лоренца с уравнением Максвелла – Фарадея:

${\mathcal {E}}=\int _{\partial \Sigma }(\mathbf {E} +\mathbf {v} _{m}\times \mathbf {B} )\cdot \mathrm {d} \mathbf {l} =-\int _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}\cdot \mathrm {d} \Sigma +\oint _{\partial \Sigma }(\mathbf {v} _{m}\times \mathbf {B} )\cdot \mathrm {d} \mathbf {l}$

где «очень важно заметить, что (1) [ v _m ] — это скорость проводника... а не скорость элемента пути d l и (2) вообще говоря, частная производная по времени не может быть вынесен за пределы интеграла, поскольку площадь является функцией времени».

Закон Фарадея и теория относительности

Дополнительная информация: Проблема с подвижным магнитом и проводником.

Два явления

Закон Фарадея представляет собой одно уравнение, описывающее два разных явления: ЭДС движения, создаваемую магнитной силой, действующей на движущийся провод (см. силу Лоренца ), и ЭДС трансформатора, создаваемую электрической силой вследствие изменения магнитного поля (описываемую законом Максвелла). – уравнение Фарадея ).

Джеймс Клерк Максвелл обратил внимание на этот факт в своей статье 1861 года « О физических силовых линиях» . Во второй половине второй части этой статьи Максвелл дает отдельное физическое объяснение каждому из двух явлений.

Ссылки на эти два аспекта электромагнитной индукции содержатся в некоторых современных учебниках. Как утверждает Ричард Фейнман:

Таким образом, «правило потока», согласно которому ЭДС в цепи равна скорости изменения магнитного потока в цепи, применяется независимо от того, изменяется ли поток из-за изменения поля или из-за движения цепи (или того и другого)...

Однако в нашем объяснении правила мы использовали два совершенно разных закона для этих двух случаев – v × B для «движений цепи» и ∇ × E = −∂ _t B для «изменений поля».

Мы не знаем другого места в физике, где такой простой и точный общий принцип требует для своего реального понимания анализа в терминах двух различных явлений .

- Ричард П. Фейнман, Фейнмановские лекции по физике

Объяснение на основе четырехмерного формализма

В общем случае объяснение появления ЭДС движения действием магнитной силы на заряды в движущемся проводе или в цепи, меняющей свою площадь, неудовлетворительно. Ведь заряды в проводе или в цепи могут вообще отсутствовать, исчезнет ли тогда в этом случае эффект электромагнитной индукции? Данная ситуация анализируется в статье, в которой при записи интегральных уравнений электромагнитного поля в четырехмерной ковариантной форме в законе Фарадея вместо частной производной по времени появляется полная производная по времени магнитного потока через цепь. . Таким образом, электромагнитная индукция появляется либо при изменении магнитного поля во времени, либо при изменении площади контура. С физической точки зрения лучше говорить не об ЭДС индукции, а о напряженности индуцированного электрического поля. ${\textstyle \mathbf {E} =-\nabla {\mathcal {E}}-{\frac {\partial \mathbf {A} }{\partial t}}}$, возникающее в цепи при изменении магнитного потока. В этом случае вклад в $\mathbf {E}$ от изменения магнитного поля осуществляется через член ${\textstyle -{\frac {\partial \mathbf {A} }{\partial t}}}$ , где $\mathbf {A}$ векторный потенциал. Если площадь контура изменяется в условиях постоянного магнитного поля, то какая-то часть контура неизбежно движется, и электрическое поле $\mathbf {E}$ возникает в этой части контура в сопутствующей системе отсчета К' в результате лоренцевского преобразования магнитного поля $\mathbf {B}$, присутствующий в стационарной системе отсчёта K, проходящей через схему. Наличие поля $\mathbf {E}$ в К' рассматривается как результат действия индукции в движущемся контуре независимо от того, присутствуют в контуре заряды или нет. В проводящей цепи поле $\mathbf {E}$ вызывает движение зарядов. В системе отсчета К это выглядит как появление ЭДС индукции ${\mathcal {E}}$, градиент которого в виде $-\nabla {\mathcal {E}}$, взятая по схеме, по-видимому, порождает поле $\mathbf {E}$.

Взгляд Эйнштейна

Размышление над этой кажущейся дихотомией было одним из основных путей, которые привели Альберта Эйнштейна к разработке специальной теории относительности :

Известно, что электродинамика Максвелла — в ее обычном понимании в настоящее время — применительно к движущимся телам приводит к асимметриям, которые, по-видимому, не присущи этим явлениям. Возьмем, к примеру, взаимное электродинамическое действие магнита и проводника.

Наблюдаемое здесь явление зависит только от относительного движения проводника и магнита, тогда как общепринятый взгляд проводит резкое различие между двумя случаями, когда движется либо то, либо другое из этих тел. Ибо если магнит находится в движении, а проводник покоится, то вблизи магнита возникает электрическое поле с некоторой определенной энергией, производящее ток в местах расположения частей проводника.

Но если магнит неподвижен, а проводник находится в движении, то вблизи магнита никакого электрического поля не возникает. Однако в проводнике мы обнаруживаем электродвижущую силу, которой самой по себе не существует соответствующей энергии, но которая порождает — при условии равенства относительного движения в двух обсуждаемых случаях — электрические токи того же пути и интенсивности, что и те, которые возникают в первом случае электрическими силами.

Примеры такого рода вместе с безуспешными попытками обнаружить какое-либо движение Земли относительно «легкой среды» позволяют предположить, что явления электродинамики, как и механики, не обладают никакими свойствами, соответствующими идее абсолютного покоя.

— Альберт Эйнштейн , «К электродинамике движущихся тел».

См. также

• вихревой ток
• Индуктивность
• Уравнения Максвелла
• Перекрестные помехи
• Парадокс Фарадея
• Закон Феличи

Дальнейшее чтение

• Клерк Максвелл, Джеймс (1881). Трактат об электричестве и магнетизме, Vol. II . Оксфорд: Кларендон Пресс. гл. III, сек. 530, с. 178. ИСБН  0-486-60637-6 . Трактат об электричестве и магнетизме.

Внешние ссылки

• СМИ, связанные с законом индукции Фарадея, на Викискладе?
• Простое интерактивное руководство по электромагнитной индукции (нажмите и перетащите магнит вперед и назад) Национальная лаборатория сильных магнитных полей
• Роберто Вега. Индукция: закон Фарадея и закон Ленца – анимированная лекция со звуковыми эффектами , страница курса «Электричество и магнетизм»
• Заметки по физике и астрономии Гиперфизика в Университете штата Джорджия
• Танкерсли и Моска: Знакомство с законом Фарадея
• Бесплатное моделирование ЭДС движения