Электростатика

Пенопластовый арахис прилипает к кошачьей шерсти из-за статического электричества . Электрическое поле заряженного меха вызывает поляризацию молекул пены за счет электростатической индукции , в результате чего легкие кусочки пластика слегка притягиваются к меху. Этот эффект также является причиной налипания статического электричества на одежду.

Электростатика — раздел физики , изучающий медленно движущиеся или стационарные электрические заряды .

С классических времен было известно, что некоторые материалы, например янтарь , после трения притягивают к себе легкие частицы . Греческое слово , обозначающее янтарь, ἤλεκτρον ( ḗлектрон ), стало, таким образом, источником слова электричество . Электростатические явления возникают из-за сил , с которыми электрические заряды действуют друг на друга. Такие силы описываются законом Кулона .

Существует множество примеров электростатических явлений: от таких простых, как притягивание полиэтиленовой пленки к руке после того, как ее вынули из упаковки, до очевидно самопроизвольных взрывов зернохранилищ, повреждения электронных компонентов во время производства, а также фотокопировальных и лазерных устройств. работа принтера .

Электростатическая модель точно предсказывает электрические явления в «классических» случаях, когда скорости малы, а система является макроскопической, поэтому квантовые эффекты не задействованы. Это также играет роль в квантовой механике, где также необходимо включать дополнительные термины.

Закон Кулона

Основная статья: закон Кулона

Закон Кулона гласит, что:

Величина электростатической силы притяжения или отталкивания между двумя точечными зарядами прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними.

Сила направлена ​​вдоль соединяющей их прямой. Если два заряда имеют одинаковый знак, электростатическая сила между ними отталкивает; если они имеют разные знаки, сила между ними притягивается.

Если $r$ расстояние (в метрах ) между двумя зарядами, то сила между двумя точечными зарядами $q$ и $Q$ является:

$F={\frac {qQ}{4\pi \varepsilon _{0}r^{2}}}\,,$

где ε ₀ = 8,854 187 8188 (14) × 10 ⁻¹²  F⋅m ⁻¹ - диэлектрическая проницаемость вакуума .

Единица СИ ​ ε ₀ эквивалентно A ² ⋅ s ⁴ ⋅kg ⁻¹ ⋅m ⁻³ или С ² ⋅ N ⁻¹ ⋅m ⁻² или Ф⋅м ​ ⁻¹ .

Электрическое поле

Основная статья: Электрическое поле

Электростатическое поле (линии со стрелками) близлежащего положительного заряда (+) заставляет подвижные заряды в проводящих объектах разделяться из-за электростатической индукции . Отрицательные заряды (синие) притягиваются и движутся к поверхности объекта, обращенной к внешнему заряду. Положительные заряды (красные) отталкиваются и движутся к поверхности, обращенной в сторону. Эти индуцированные поверхностные заряды имеют правильный размер и форму, поэтому их противоположное электрическое поле нейтрализует электрическое поле внешнего заряда внутри металла. Следовательно, электростатическое поле повсюду внутри проводящего объекта равно нулю, а электростатический потенциал постоянен.

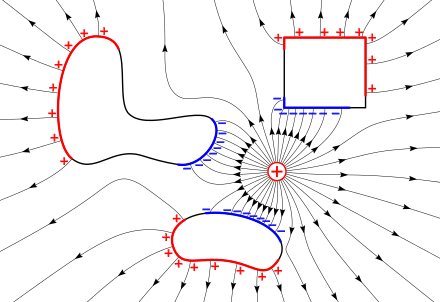
Электрическое поле, $\mathbf {E}$, в единицах Ньютонов на кулон или вольт на метр, представляет собой векторное поле , которое можно определить везде, кроме места расположения точечных зарядов (где оно расходится до бесконечности). Она определяется как электростатическая сила $\mathbf {,}$ на гипотетическом небольшом пробном заряде в точке по закону Кулона, разделенном на заряд $q$

$\mathbf {E} ={\mathbf {F} \over q}$

Линии электрического поля полезны для визуализации электрического поля. Линии поля начинаются при положительном заряде и заканчиваются при отрицательном заряде. Они параллельны направлению электрического поля в каждой точке, а плотность этих силовых линий является мерой величины электрического поля в любой данной точке.

Рассмотрим коллекцию $n$ частицы заряда $q_{i}$, расположенный в точках $\mathbf {r} _{i}$ (так называемые точки источника ), электрическое поле в $\mathbf {r}$ (называемая точкой поля ):

$\mathbf {E} (\mathbf {r} )={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{{\hat {\mathbf {r} }}_{i} \over {|\mathbf {r} _{i}|}^{2}}={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{i}{\mathbf {r} _{i} \over {|\mathbf {r} _{i}|}^{3}},$

где ${\textstyle \mathbf {r} _{i}=\mathbf {r} -\mathbf {r} _{i}}$ вектор смещения от исходной точки $\mathbf {r} _{i}$ до точки поля $\mathbf {r}$, и ${\textstyle {\hat {\mathbf {r} }}_{i}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathbf {r} _{i}}{|\mathbf {r} _{i}|}}}$ — единичный вектор , указывающий направление поля. Для одного точечного заряда в начале координат величина этого электрического поля равна $E=Q/4\pi \varepsilon _{0}r^{2}$ и указывает в сторону от этого заряда, если он положительный. Тот факт, что сила (и, следовательно, поле) может быть рассчитана путем суммирования всех вкладов, вносимых отдельными исходными частицами, является примером принципа суперпозиции . Электрическое поле, создаваемое распределением зарядов, определяется объемной плотностью заряда. $\rho (\mathbf {r} )$ и может быть получен путем преобразования этой суммы в тройной интеграл :

$\mathbf {E} (\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\iiint \,\rho (\mathbf {r} '){\mathbf {r} ' \over {|\mathbf {r} '|}^{3}}\mathrm {d} ^{3}|\mathbf {r} '|$

Закон Гаусса

Основные статьи: закон Гаусса и гауссова поверхность

Закон Гаусса утверждает, что «полный электрический поток через любую замкнутую поверхность в свободном пространстве любой формы, нарисованную в электрическом поле, пропорционален общему электрическому заряду, заключенному в этой поверхности». Многие численные задачи можно решить, рассматривая гауссову поверхность вокруг тела. Математически закон Гаусса принимает форму интегрального уравнения:

$\Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={Q_{\text{enclosed}} \over \varepsilon _{0}}=\int _{V}{\rho \over \varepsilon _{0}}\mathrm {d} ^{3}r,$

где $\mathrm {d} ^{3}r=\mathrm {d} x\ \mathrm {d} y\ \mathrm {d} z$ является элементом объема. Если заряд распределен по поверхности или вдоль линии, замените $\rho \,\mathrm {d} ^{3}r$ к $\sigma \,\mathrm {d} A$ или $\lambda \,\mathrm {d} \ell$. Теорема о дивергенции позволяет записать закон Гаусса в дифференциальной форме:

${\vec {\nabla }}\cdot {\vec {E}}={\rho \over \varepsilon _{0}}.$

где ${\vec {\nabla }}\cdot$ — оператор дивергенции .

и

Основные статьи: уравнение Пуассона и уравнение Лапласа

Определение электростатического потенциала в сочетании с дифференциальной формой закона Гаусса (см. выше) обеспечивает связь между потенциалом Φ и плотностью заряда ρ :

${\nabla }^{2}\phi =-{\rho \over \varepsilon _{0}}.$

Это соотношение представляет собой форму уравнения Пуассона . В отсутствие неспаренного электрического заряда уравнение становится уравнением Лапласа :

${\nabla }^{2}\phi =0,$

Электростатическое приближение

Справедливость электростатического приближения основана на предположении, что электрическое поле является безвихревым :

${\vec {\nabla }}\times {\vec {E}}=0.$

Из закона Фарадея это предположение подразумевает отсутствие или почти отсутствие изменяющихся во времени магнитных полей:

${\partial {\vec {B}} \over \partial t}=0.$

Другими словами, электростатика не требует отсутствия магнитных полей или электрических токов. Скорее, если магнитные поля или электрические токи действительно существуют, они не должны меняться со временем или, в худшем случае, они должны меняться со временем очень медленно . В некоторых задачах для точных предсказаний могут потребоваться как электростатика, так и магнитостатика , но связь между ними все равно можно игнорировать. Электростатику и магнитостатику можно рассматривать как нерелятивистские галилеевские пределы электромагнетизма. Кроме того, традиционная электростатика игнорирует квантовые эффекты, которые необходимо добавить для полного описания.

Электростатический потенциал

Основная статья: Электростатический потенциал

Поскольку электрическое поле является безвихревым , его можно выразить как градиент скалярной функции: $\phi$, называемый электростатическим потенциалом (также известным как напряжение ). Электрическое поле, $E$, точки от областей с высоким электрическим потенциалом к ​​областям с низким электрическим потенциалом, математически выраженные как

${\vec {E}}=-{\vec {\nabla }}\phi .$

Теорему о градиенте можно использовать, чтобы установить, что электростатический потенциал — это количество работы на единицу заряда, необходимое для перемещения заряда из точки $a$ указывать $b$ со следующим линейным интегралом :

$-\int _{a}^{b}{{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}}=\phi ({\vec {b}})-\phi ({\vec {a}}).$

Из этих уравнений мы видим, что электрический потенциал постоянен в любой области, в которой электрическое поле исчезает (например, внутри проводящего объекта).

Электростатическая энергия

Основные статьи: Электрическая потенциальная энергия и плотность энергии

частицы Потенциальная энергия пробной , $U_{\mathrm {E} }^{\text{single}}$, можно вычислить из линейного интеграла работы, $q_{n}{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}$. Мы интегрируем от точки бесконечности и предполагаем набор $N$ частицы заряда $Q_{n}$, уже расположены в точках ${\vec {r}}_{i}$. Эта потенциальная энергия (в Джоулях ):

$U_{\mathrm {E} }^{\text{single}}=q\phi ({\vec {r}})={\frac {q}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\frac {Q_{i}}{\left\|{\mathcal {{\vec {R}}_{i}}}\right\|}}$

где ${\vec {\mathcal {R_{i}}}}={\vec {r}}-{\vec {r}}_{i}$ расстояние каждого заряда $Q_{i}$ из тестового заряда $q$, который находится в точке ${\vec {r}}$, и $\phi ({\vec {r}})$ электрический потенциал, который будет при ${\vec {r}}$ если испытательный заряд отсутствовал. Если присутствуют только два заряда, потенциальная энергия равна $Q_{1}Q_{2}/(4\pi \varepsilon _{0}r)$. Полная электрическая потенциальная энергия, обусловленная совокупностью N зарядов, рассчитывается путем сборки этих частиц по одной :

$U_{\mathrm {E} }^{\text{total}}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{j=1}^{N}Q_{j}\sum _{i=1}^{j-1}{\frac {Q_{i}}{r_{ij}}}={\frac {1}{2}}\sum _{i=1}^{N}Q_{i}\phi _{i},$

где следующая сумма от j = 1 до N исключает i = j :

$\phi _{i}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{\stackrel {j=1}{j\neq i}}^{N}{\frac {Q_{j}}{r_{ij}}}.$

Этот электрический потенциал, $\phi _{i}$ это то, что будет измерено при ${\vec {r}}_{i}$ если заряд $Q_{i}$ отсутствовали. Эта формула, очевидно, исключает (бесконечную) энергию, которая потребовалась бы для сборки каждого точечного заряда из дисперсного облака зарядов. Сумма по зарядам может быть преобразована в интеграл по плотности заряда с помощью рецепта ${\textstyle \sum (\cdots )\rightarrow \int (\cdots )\rho \,\mathrm {d} ^{3}r}$:

$U_{\mathrm {E} }^{\text{total}}={\frac {1}{2}}\int \rho ({\vec {r}})\phi ({\vec {r}})\,\mathrm {d} ^{3}r={\frac {\varepsilon _{0}}{2}}\int \left|{\mathbf {E} }\right|^{2}\,\mathrm {d} ^{3}r,$

Это второе выражение для электростатической энергии использует тот факт, что электрическое поле представляет собой отрицательный градиент электрического потенциала, а также тождества векторного исчисления , напоминающие интегрирование по частям . Эти два интеграла для энергии электрического поля, по-видимому, указывают на две взаимоисключающие формулы для плотности электростатической энергии, а именно: ${\textstyle {\frac {1}{2}}\rho \phi }$ и ${\textstyle {\frac {1}{2}}\varepsilon _{0}E^{2}}$; они дают равные значения полной электростатической энергии только в том случае, если обе они интегрированы по всему пространству.

Электростатическое давление

На проводнике поверхностный заряд будет испытывать силу в присутствии электрического поля . Эта сила представляет собой среднее значение разрывного электрического поля на поверхностном заряде. Это среднее значение поля вне поверхности составляет:

$P={\frac {\varepsilon _{0}}{2}}E^{2},$

Это давление стремится втянуть проводник в поле независимо от знака поверхностного заряда.

См. также

• Электромагнетизм - фундаментальное взаимодействие между заряженными частицами.
• Электростатический генератор , машины, создающие статическое электричество.
• Электростатическая индукция , разделение зарядов за счет электрических полей.
• Диэлектрическая проницаемость и относительная диэлектрическая проницаемость , электрическая поляризуемость материалов.
• Квантование заряда , единиц заряда, переносимых электронами или протонами.
• Статическое электричество , стационарный заряд, накопленный на материале.
• Трибоэлектрический эффект , разделение зарядов за счет скольжения или контакта.

Дальнейшее чтение

• Герман А. Хаус; Джеймс Р. Мельчер (1989). Электромагнитные поля и энергия . Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. ISBN  0-13-249020-Х .
• Холлидей, Дэвид; Роберт Резник; Кеннет С. Крейн (1992). Физика . Нью-Йорк: Джон Уайли и сыновья. ISBN  0-471-80457-6 .
• Гриффитс, Дэвид Дж . (1999). Введение в электродинамику . Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл. ISBN  0-13-805326-Х .

Внешние ссылки

• СМИ, связанные с электростатикой, на Викискладе?

• Фейнмановские лекции по физике Vol. II гл. 4: Электростатика
• Введение в электростатику : точечные заряды можно рассматривать как распределение с использованием дельта-функции Дирака.

Учебные материалы по электростатике в Викиверситете