Ступенчатая функция Хевисайда

Шаг Хевисайда
Ступенчатая функция Хевисайда с использованием соглашения о полувысоте.
Общая информация
Общее определение	$$H(x):={\begin{cases}1,&x\geq 0\\0,&x<0\end{cases}}$$
Области применения	Операционное исчисление

Ступенчатая функция Хевисайда , или единичная ступенчатая функция , обычно обозначаемая H или θ (но иногда u , 1 или 𝟙 ), представляет собой ступенчатую функцию, названную в честь Оливера Хевисайда , значение которой равно нулю для отрицательных аргументов и единице для неотрицательных аргументов. . Это пример общего класса ступенчатых функций, все из которых могут быть представлены как линейные комбинации преобразований этой функции.

Функция изначально была разработана в операционном исчислении для решения дифференциальных уравнений , где она представляет собой сигнал, который включается в определенное время и остается включенным на неопределенный срок. Оливер Хевисайд , разработавший операционное исчисление как инструмент анализа телеграфных сообщений, представил функцию как 1 .

Функция Хевисайда может быть определена как:

• функция кусочная :
  $$H(x):={\begin{cases}1,&x\geq 0\\0,&x<0\end{cases}}$$
• используя обозначение скобки Айверсона :
  $$H(x):=[x\geq 0]$$
• индикаторная функция :
  $$H(x):=\mathbf {1} _{x\geq 0}=\mathbf {1} _{\mathbb {R} _{+}}(x)$$
• производная функции линейного изменения :
  $$H(x):={\frac {d}{dx}}\max\{x,0\}\quad {\mbox{for }}x\neq 0$$

Дельта- функция Дирака является производной функции Хевисайда.

$$\delta (x)={\frac {d}{dx}}H(x)$$

Следовательно, функцию Хевисайда можно рассматривать как интеграл дельта-функции Дирака. Иногда это пишут как

$$H(x):=\int _{-\infty }^{x}\delta (s)\,ds$$

хотя это разложение может не выполняться (или даже иметь смысл) для x = 0 , в зависимости от того, какой формализм используется для придания смысла интегралам, включающим δ . В этом контексте функция Хевисайда представляет собой кумулятивную функцию распределения , случайной величины которая почти наверняка равна 0. (См. Постоянная случайная величина .)

В операционном исчислении полезные ответы редко зависят от того, какое значение используется для H (0) , поскольку H чаще всего используется в качестве распределения . Однако этот выбор может иметь некоторые важные последствия в функциональном анализе и теории игр, где рассматриваются более общие формы непрерывности. Некоторые распространенные варианты можно увидеть ниже .

Аппроксимации ступенчатой ​​функции Хевисайда используются в биохимии и нейробиологии , где логистические аппроксимации ступенчатых функций (такие как уравнения Хилла и Михаэлиса-Ментен ) могут использоваться для аппроксимации бинарных клеточных переключателей в ответ на химические сигналы.

Аналитические приближения

${\tfrac {1}{2}}+{\tfrac {1}{2}}\tanh(kx)={\frac {1}{1+e^{-2kx}}}$
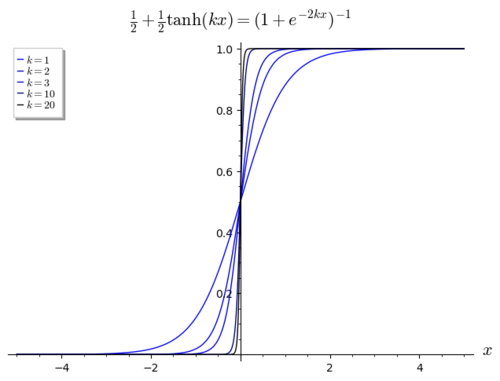
приближается к ступенчатой ​​функции при k → ∞ .

Для плавного приближения к ступенчатой ​​функции можно использовать логистическую функцию

$$H(x)\approx {\tfrac {1}{2}}+{\tfrac {1}{2}}\tanh kx={\frac {1}{1+e^{-2kx}}},$$

где большее значение k соответствует более резкому переходу при x = 0 . Если взять H (0) = 1/2 равенство имеет место в : пределе

$$H(x)=\lim _{k\to \infty }{\tfrac {1}{2}}(1+\tanh kx)=\lim _{k\to \infty }{\frac {1}{1+e^{-2kx}}}.$$

Существует множество других гладких аналитических приближений ступенчатой ​​функции. Среди возможностей:

$${\begin{aligned}H(x)&=\lim _{k\to \infty }\left({\tfrac {1}{2}}+{\tfrac {1}{\pi }}\arctan kx\right)\\H(x)&=\lim _{k\to \infty }\left({\tfrac {1}{2}}+{\tfrac {1}{2}}\operatorname {erf} kx\right)\end{aligned}}$$

Эти пределы справедливы поточечно и в смысле распределений . Однако в целом поточечная сходимость не обязательно влечет за собой сходимость по распределению, и наоборот, сходимость по распределению не обязательно влечет за собой поточечную сходимость. (Однако если все члены поточечно сходящейся последовательности функций равномерно ограничены некоторой «хорошей» функцией, то сходимость имеет место и в смысле распределений .)

В общем, любая кумулятивная функция распределения непрерывного может распределения вероятностей , имеющая максимум около нуля и имеющая параметр, контролирующий дисперсию, служить приближением в том пределе, когда дисперсия приближается к нулю. Например, все три приведенных выше приближения являются кумулятивными функциями распределения общих вероятностных распределений: логистического , Коши и нормального распределения соответственно.

Интегральные представления

Часто бывает полезно интегральное представление ступенчатой ​​функции Хевисайда:

$${\begin{aligned}H(x)&=\lim _{\varepsilon \to 0^{+}}-{\frac {1}{2\pi i}}\int _{-\infty }^{\infty }{\frac {1}{\tau +i\varepsilon }}e^{-ix\tau }d\tau \\&=\lim _{\varepsilon \to 0^{+}}{\frac {1}{2\pi i}}\int _{-\infty }^{\infty }{\frac {1}{\tau -i\varepsilon }}e^{ix\tau }d\tau .\end{aligned}}$$

где второе представление легко вывести из первого, учитывая, что ступенчатая функция действительна и, следовательно, является своей собственной комплексно-сопряженной.

Нулевой аргумент

Поскольку при интегрировании обычно используется H , а значение функции в отдельной точке не влияет на ее интеграл, редко имеет значение, какое именно значение выбрано из H (0) . Действительно, когда H рассматривается как распределение или элемент L ^∞ (см . Л ^п space ) о значении в нуле даже говорить не имеет смысла, так как такие объекты только почти везде определены . Если используется какое-то аналитическое приближение (как в примерах выше ), то часто используется соответствующий предел в нуле.

Существуют различные причины для выбора того или иного значения.

• Ч (0) = тогда граф ; Часто используется 1/2, поскольку обладает вращательной симметрией другими словами, H — 1/2 является функцией тогда нечетной . справедливо следующее соотношение со знаковой функцией В этом случае для всех x :
  $$H(x)={\tfrac {1}{2}}(1+\operatorname {sgn} x).$$
• H (0) = 1 используется, когда H должно быть непрерывным справа . Например, кумулятивные функции распределения обычно считаются непрерывными справа, как и функции, интегрированные в интегрировании Лебега – Стилтьеса . В этом случае H — функция замкнутого индикаторная полубесконечного интервала:
  $$H(x)=\mathbf {1} _{[0,\infty )}(x).$$
  Соответствующее распределение вероятностей является вырожденным распределением .
• H (0) = 0 используется, когда H должен быть непрерывным слева . В этом случае H является индикаторной функцией открытого полубесконечного интервала:
  $$H(x)=\mathbf {1} _{(0,\infty )}(x).$$
• В контексте функционального анализа из оптимизации и теории игр часто полезно определить функцию Хевисайда как многозначную функцию, чтобы сохранить непрерывность предельных функций и гарантировать существование определенных решений. В этих случаях функция Хевисайда возвращает целый интервал возможных решений H (0) = [0,1] .

Дискретная форма

Альтернативная форма единичного шага, определяемая вместо этого как функция $H:\mathbb {Z} \rightarrow \mathbb {R}$ (то есть, приняв дискретную переменную n ), есть:

$$H[n]={\begin{cases}0,&n<0,\\1,&n\geq 0,\end{cases}}$$

или используя соглашение о полувысоте:

$$H[n]={\begin{cases}0,&n<0,\\{\tfrac {1}{2}},&n=0,\\1,&n>0,\end{cases}}$$

где n — целое число . Если n — целое число, то n < 0 должно означать, что n ≤ −1 , а n > 0 должно означать, что функция достигает единицы при n = 1 . Следовательно, «ступенчатая функция» демонстрирует линейное поведение в области [-1, 1] и не может быть подлинно ступенчатой ​​функцией, используя соглашение о полувысоте.

В отличие от непрерывного случая, определение H [0] существенно.

Единичный импульс дискретного времени - это первая разность шага дискретного времени.

$$\delta [n]=H[n]-H[n-1].$$

Эта функция представляет собой совокупное суммирование дельты Кронекера :

$$H[n]=\sum _{k=-\infty }^{n}\delta [k]$$

где

$$\delta [k]=\delta _{k,0}$$

– дискретная единичная импульсная функция .

Первообразная и производная

Функция линейного изменения является производной ступенчатой ​​функции Хевисайда:

$$\int _{-\infty }^{x}H(\xi )\,d\xi =xH(x)=\max\{0,x\}\,.$$

Распределительная производная ступенчатой ​​функции Хевисайда представляет собой дельта-функцию Дирака :

$${\frac {dH(x)}{dx}}=\delta (x)\,.$$

Преобразование Фурье

ступенчатой Преобразование Фурье ​​функции Хевисайда представляет собой распределение. Используя один выбор констант для определения преобразования Фурье, мы имеем

$${\hat {H}}(s)=\lim _{N\to \infty }\int _{-N}^{N}e^{-2\pi ixs}H(x)\,dx={\frac {1}{2}}\left(\delta (s)-{\frac {i}{\pi }}\operatorname {p.v.} {\frac {1}{s}}\right).$$

Здесь пв 1 / s — это распределение , которое переводит пробную функцию φ в Коши главное значение $\textstyle \int _{-\infty }^{\infty }{\frac {\varphi (s)}{s}}\,ds$. Предел, входящий в интеграл, также понимается в смысле (умеренных) распределений.

Одностороннее

Преобразование Лапласа ступенчатой ​​функции Хевисайда является мероморфной функцией . Используя одностороннее преобразование Лапласа, имеем:

$${\begin{aligned}{\hat {H}}(s)&=\lim _{N\to \infty }\int _{0}^{N}e^{-sx}H(x)\,dx\\&=\lim _{N\to \infty }\int _{0}^{N}e^{-sx}\,dx\\&={\frac {1}{s}}\end{aligned}}$$

При использовании двустороннего преобразования интеграл можно разделить на две части, и результат будет одинаковым.

Другие выражения

Ступенчатую функцию Хевисайда можно представить в виде гиперфункции следующим образом:

$$H(x)=\left(1-{\frac {1}{2\pi i}}\log z,\ -{\frac {1}{2\pi i}}\log z\right).$$

где log z — комплексного логарифма z . главное значение

это также можно выразить Для x ≠ 0 через функцию абсолютного значения как

$$H(x)={\frac {x+|x|}{2x}}\,.$$

См. также

• Дельта-функция Дирака
• Функция индикатора
• Кронштейн Айверсона
• Преобразование Лапласа
• Лапласиан индикатора
• Список математических функций
• Брекеты Маколея
• Отрицательное число
• Прямоугольная функция
• Функция знака
• Синусоидальный интеграл
• Шаговый отклик

Внешние ссылки

• Цифровая библиотека математических функций, NIST, [1] .
• Берг, Эрнст Юлиус (1936). «Единичная функция». Операционное исчисление Хевисайда применительно к технике и физике . Макгроу-Хилл Образование . п. 5.
• Калверт, Джеймс Б. (2002). «Хевисайд, Лаплас и интеграл инверсии» . Денверский университет .
• Дэвис, Брайан (2002). «Ступенчатая функция Хевисайда». Интегральные преобразования и их приложения (3-е изд.). Спрингер. п. 28.
• Дафф, Джордж Ф.Д .; Нейлор, Д. (1966). «Функция единицы Хевисайда». Дифференциальные уравнения прикладной математики . Джон Уайли и сыновья . п. 42.