интеграл

Эта статья о понятии определенных интегралов в исчислении. Чтобы узнать о неопределенном интеграле, см. первообразную . Чтобы узнать о наборе чисел, см. целое число . Чтобы узнать о других значениях, см. Интеграл (значения) .

«Площадь под кривой» перенаправляется сюда. Чтобы узнать о фармакологическом интеграле, см. Площадь под кривой (фармакокинетика) . Понятие статистики см. в разделе Рабочая характеристика приемника § Площадь под кривой .

Определенный интеграл функции можно представить как знаковую область области, ограниченную ее графиком и горизонтальной осью; на приведенном выше графике в качестве примера интеграл от $f(x)$ это желтая (-) область, вычтенная из синей (+) области

В математике интеграл — это непрерывный аналог суммы , который используется для вычисления площадей , объёмов и их обобщений. Интегрирование, процесс вычисления интеграла, является одной из двух фундаментальных операций исчисления . другой — дифференциация . Первоначально интегрирование использовалось для решения задач по математике и физике , таких как нахождение площади под кривой или определение смещения по скорости. После этого использование интеграции распространилось на самые разные научные области.

Определенный интеграл вычисляет знаковую площадь области на плоскости, ограниченной графиком заданной функции между двумя точками на действительной линии . Обычно области выше горизонтальной оси плоскости являются положительными, а области ниже - отрицательными. Интегралы также относятся к понятию первообразной , функции, производной которой является данная функция; в этом случае их еще называют неопределенными интегралами . Фундаментальная теорема исчисления связывает определенное интегрирование с дифференцированием и обеспечивает метод вычисления определенного интеграла функции, когда известна ее первообразная; дифференцирование и интегрирование — обратные операции.

Хотя методы расчета площадей и объемов восходят к древнегреческой математике , принципы интегрирования были сформулированы независимо Исааком Ньютоном и Готфридом Вильгельмом Лейбницем в конце 17 века, которые думали о площади под кривой как о бесконечной сумме прямоугольников бесконечно малой ширины. . Позже Бернхард Риман дал строгое определение интегралов, основанное на предельной процедуре, аппроксимирующей площадь криволинейной области путем разбиения этой области на бесконечно тонкие вертикальные пластины. В начале 20 века Анри Лебег обобщил формулировку Римана, введя то, что сейчас называется интегралом Лебега ; он более общий, чем римановский, в том смысле, что более широкий класс функций интегрируем по Лебегу.

Интегралы могут быть обобщены в зависимости от типа функции, а также области , в которой выполняется интегрирование. Например, линейный интеграл для функций двух и более переменных определяется , а интервал интегрирования заменяется кривой, соединяющей две точки пространства. В поверхностном интеграле кривая заменяется частью поверхности в трехмерном пространстве .

История

Смотрите также: История исчисления

Предварительная интеграция

Первым документально подтвержденным систематическим методом, позволяющим определять интегралы, является метод исчерпывания, предложенный древнегреческим астрономом Евдоксом и философом Демокритом ( ок. 370 г. до н.э.), которые стремились найти площади и объемы, разбивая их на бесконечное число делений, для которых площадь или объем были известны. Этот метод был далее развит и использован Архимедом в III веке до нашей эры и использовался для расчета площади круга , площади поверхности и объема сферы . , площади эллипса , площади под параболой , объема сегмента параболоид вращения , объем сегмента гиперболоида вращения и площадь спирали .

Похожий метод был независимо разработан в Китае примерно в III веке нашей эры Лю Хуэем , который использовал его для определения площади круга. Позже этот метод был использован в V веке китайскими математиками, отцом и сыном Цзу Чунчжи и Цзу Гэном, чтобы найти объем сферы.

На Ближнем Востоке Хасан ибн аль-Хайсам, латинизированный как Альхазен ( ок. 965 – ок. 1040 г. н. э.), вывел формулу суммы четвертых степеней . Альхазен определил уравнения для расчета площади, ограниченной кривой, представленной формулой $y=x^{k}$ (что переводится как интеграл $\int x^{k}\,dx$ в современных обозначениях) для любого заданного неотрицательного целого значения $k$. Он использовал результаты для выполнения того, что сейчас будет называться интегрированием этой функции, где формулы для сумм целых квадратов и четвертых степеней позволили ему вычислить объем параболоида .

Следующие значительные достижения в интегральном исчислении стали появляться только в 17 веке. В это время работы Кавальери с его методом неделимых и работы Ферма начали закладывать основы современного исчисления. с Кавальери, вычисляющим интегралы от x ^н до степени n = 9 в квадратурной формуле Кавальери . Случай n = −1 потребовал изобретения функции гиперболического логарифма , полученной квадратурой гиперболы . в 1647 году

Дальнейшие шаги были сделаны в начале 17 века Барроу и Торричелли , которые дали первые намеки на связь между интеграцией и дифференциацией . Барроу предоставил первое доказательство фундаментальной теоремы исчисления . Уоллис обобщил метод Кавальери, вычисляя интегралы от x до общей степени, включая отрицательные и дробные степени.

Лейбниц и Ньютон

Главный прогресс в интеграции произошел в 17 веке с независимым открытием теоремы исчисления и фундаментальной Ньютоном Лейбницем . Теорема демонстрирует связь между интегрированием и дифференцированием. Эту связь в сочетании со сравнительной легкостью дифференцирования можно использовать для вычисления интегралов. В частности, основная теорема исчисления позволяет решать гораздо более широкий класс задач. Не менее важна и всеобъемлющая математическая основа, разработанная Лейбницем и Ньютоном. Учитывая название «исчисление бесконечно малых», оно позволяло проводить точный анализ функций с непрерывными областями определения. Эта структура в конечном итоге стала современным исчислением , обозначения интегралов которого взяты непосредственно из работ Лейбница.

Формализация

Хотя Ньютон и Лейбниц предложили систематический подход к интеграции, их работе не хватало некоторой строгости . Епископ Беркли подверг резкой критике исчезающие приращения, использованные Ньютоном, назвав их « призраками ушедших величин ». Исчисление приобрело более прочную основу с развитием пределов . Интеграция была впервые строго формализована с использованием пределов Риманом . Хотя все ограниченные кусочно- непрерывные функции интегрируемы по Риману на ограниченном интервале, впоследствии были рассмотрены более общие функции — особенно в контексте анализа Фурье — к которым определение Римана не применимо, и Лебег сформулировал другое определение интеграла , основанное на мере теория (подобласть реального анализа ). Были предложены и другие определения интеграла, расширяющие подходы Римана и Лебега. Эти подходы, основанные на действительной системе счисления, являются наиболее распространенными сегодня, но существуют альтернативные подходы, такие как определение интеграла как стандартной части бесконечной суммы Римана, основанное на гипердействительной системе счисления .

Историческая справка

Обозначение неопределенного интеграла было введено Готфридом Вильгельмом Лейбницем в 1675 году. Он адаптировал символ интегральный ∫ из буквы ſ ( длинное s ), обозначающей сумму (пишется как ſumma ; на латыни означает «сумма» или «общее количество»). Современные обозначения определенного интеграла с пределами выше и ниже знака интеграла были впервые использованы Жозефом Фурье в «Мемуарах Французской академии» около 1819–1820 годов и перепечатаны в его книге 1822 года.

Исаак Ньютон использовал небольшую вертикальную черту над переменной для обозначения интегрирования или помещал переменную в рамку. Вертикальную черту легко спутать с . x или x ′ , которые используются для обозначения дифференциации, а обозначение прямоугольника было трудно воспроизвести принтерам, поэтому эти обозначения не получили широкого распространения.

Первое использование термина

Этот термин был впервые напечатан на латыни Якобом Бернулли в 1690 году: «Ergo et horum Integralia aequantur».

Терминология и обозначения

В общем, интеграл действительной функции f ( x ) по действительной переменной x на интервале [ a , b ] записывается как

$\int _{a}^{b}f(x)\,dx.$

Знак интеграла ∫ представляет собой интегрирование. Символ dx , называемый дифференциалом переменной x , указывает, что переменной интегрирования является x . Функция f ( x ) называется подынтегральной функцией, точки a и b называются пределами (или границами) интегрирования, а интеграл называется интервалом [ a , b ] , называемым интервалом интегрирования. Функция называется интегрируемой, если ее интеграл по области определения конечен. Если указаны пределы, интеграл называется определенным.

Когда пределы опущены, как в

$\int f(x)\,dx,$

интеграл называется неопределенным интегралом, который представляет класс функций ( первообразная ), производная которых является подынтегральной функцией. Основная теорема исчисления связывает вычисление определенных интегралов с неопределенными интегралами. Существует несколько расширений обозначения интегралов, позволяющих включать интегрирование в неограниченных областях и/или в нескольких измерениях (см. последующие разделы этой статьи).

В расширенных настройках нередко не учитывают dx , когда используется только простой интеграл Римана или точный тип интеграла неважен. Например, можно написать ${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$ чтобы выразить линейность интеграла - свойство, присущее интегралу Римана и всем его обобщениям.

Интерпретации

Приближения к интегралу √ x от 0 до 1, с 5 желтыми разделами правой конечной точки и 10 зелеными разделами левой конечной точки.

Интегралы встречаются во многих практических ситуациях. Например, по длине, ширине и глубине бассейна прямоугольной формы с плоским дном можно определить объем воды, который он может содержать, площадь его поверхности и длину края. А вот если она овальная с закругленным низом, то для нахождения точных и строгих значений этих величин требуются интегралы. В каждом случае искомую величину можно разделить на бесконечное множество бесконечно малых частей, а затем суммировать эти части для достижения точного приближения.

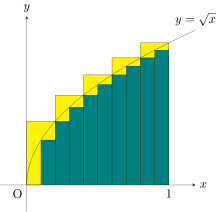
В качестве другого примера, чтобы найти площадь области, ограниченной графиком функции f ( x ) = ${\textstyle {\sqrt {x}}}$ между x = 0 и x = 1 , можно разделить интервал на пять частей ( 0, 1/5, 2/5, ..., 1 ), затем построить прямоугольники, используя высоту правого конца каждой части (таким образом, √ 0 , √ 1/5 , √ 2/5 , ..., √ 1 ) и суммируем их площади, чтобы получить аппроксимацию

$\textstyle {\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0.7497,$

что больше точного значения. Альтернативно, при замене этих подинтервалов на интервалы с высотой левого конца каждого фрагмента получаемая аппроксимация слишком низкая: при двенадцати таких подинтервалах аппроксимируемая площадь составляет всего 0,6203. Однако когда количество частей увеличивается до бесконечности, оно достигает предела, который равен точному значению искомой площади (в данном случае 2/3 ). Один пишет

$\int _{0}^{1}{\sqrt {x}}\,dx={\frac {2}{3}},$

что означает, что 2/3 является результатом взвешенной суммы значений функции √ x , умноженной на бесконечно малую ширину шага, обозначаемую dx , на интервале [0, 1] .

Суммы Дарбу

Верхние суммы Дарбу функции y = x ²

Нижние суммы Дарбу функции y = x ²

Формальные определения

Суммы Римана сходящиеся

Существует множество способов формального определения интеграла, не все из которых эквивалентны. Различия существуют в основном для рассмотрения различных особых случаев, которые могут быть неинтегрируемы в соответствии с другими определениями, но иногда они возникают и по педагогическим причинам. Наиболее часто используемые определения — это интегралы Римана и интегралы Лебега.

Интеграл Римана

Основная статья: интеграл Римана

Интеграл Римана определяется через суммы Римана функций по размеченным разбиениям интервала. Размеченное разбиение замкнутого интервала [ a , b ] на вещественной прямой представляет собой конечную последовательность

$a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!$

Это разбивает интервал [ a , b ] на n подинтервалов [ x _{i −1} , x _i ] с индексом i , каждый из которых «помечен» определенной точкой t _i ∈ [ x _{i −1} , x _i ] . Сумма Римана функции f относительно такого размеченного разбиения определяется как

$\sum _{i=1}^{n}f(t_{i})\,\Delta _{i};$

таким образом, каждый член суммы представляет собой площадь прямоугольника с высотой, равной значению функции в выбранной точке данного подинтервала, и шириной, такой же, как ширина подинтервала, Δ _i = x _i - x _{i −1} . Сетка max такого размеченного раздела представляет собой ширину наибольшего подинтервала, образованного разделом, i _{= 1... n} Δ _i . от Интеграл Римана функции f на интервале [ a , b ] равен S , если:

Для всех $\varepsilon >0$ Существует $\delta >0$ так что для любого отмеченного раздела $[a,b]$ с сеткой менее $\delta$,

$\left|S-\sum _{i=1}^{n}f(t_{i})\,\Delta _{i}\right|<\varepsilon .$

Когда выбранные теги являются максимальным (соответственно минимальным) значением функции в каждом интервале, сумма Римана становится верхней (соответственно нижней) суммой Дарбу , что позволяет предположить тесную связь между интегралом Римана и интегралом Дарбу .

Интеграл Лебега

Основная статья: Интеграция Лебега

Интеграция Лебега

Как в теории, так и в приложениях часто представляет интерес возможность предельного перехода под интегралом. Например, часто можно построить последовательность функций, которая в подходящем смысле аппроксимирует решение проблемы. Тогда интеграл функции решения должен быть пределом интегралов аппроксимаций. Однако многие функции, которые можно получить как пределы, не интегрируются по Риману, и поэтому такие предельные теоремы не выполняются для интеграла Римана. Поэтому очень важно иметь определение интеграла, позволяющее интегрировать более широкий класс функций.

Таким интегралом является интеграл Лебега, который использует следующий факт для расширения класса интегрируемых функций: если значения функции переставляются в области определения, интеграл функции должен оставаться прежним. Так, Анри Лебег ввел интеграл, носящий его имя, объяснив этот интеграл таким образом в письме Полю Монтелю :

Я должен заплатить определенную сумму, которую я накопил в кармане. Я достаю из кармана купюры и монеты и передаю их кредитору в том порядке, в котором нахожу их, пока не наберу общую сумму. Это интеграл Римана. Но я могу поступить иначе. После того, как я вынул все деньги из кармана, я заказываю купюры и монеты одинакового достоинства, а затем выплачиваю несколько пачек одну за другой кредитору. Это мой интеграл.

Как говорит Фолланд: «Чтобы вычислить интеграл Римана от f , нужно разбить область [ a , b ] на подинтервалы», тогда как в интеграле Лебега «фактически разбивают диапазон f ». Таким образом, определение интеграла Лебега начинается с меры µ. В простейшем случае мера Лебега µ ( A ) интервала A = [ a , b ] — это его ширина b − a , так что интеграл Лебега согласуется с (собственным) интегралом Римана, когда оба существуют. В более сложных случаях измеряемые наборы могут быть сильно фрагментированы, лишены непрерывности и сходства с интервалами.

Используя философию «разделения диапазона f », интеграл неотрицательной функции f : R → R должен быть суммой по t площадей между тонкой горизонтальной полосой между y = t и y = t + dt . Эта площадь равна всего лишь µ { x : f ( x ) > t } dt . Пусть f ^∗ ( т ) знак равно μ { Икс : ж ( Икс ) > т } . Тогда интеграл Лебега от f определяется формулой

$\int f=\int _{0}^{\infty }f^{*}(t)\,dt$

где интеграл справа — это обычный несобственный интеграл Римана ( f ^∗ является строго убывающей положительной функцией и, следовательно, имеет четко определенный несобственный интеграл Римана). Для подходящего класса функций ( измеримых функций ) это определяет интеграл Лебега.

Общая измеримая функция f интегрируема по Лебегу, если сумма абсолютных значений площадей областей между графиком f и осью x конечна:

$\int _{E}|f|\,d\mu <+\infty .$

В этом случае интеграл, как и в римановом случае, представляет собой разность между площадью над осью x и площадью под осью x :

$\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu$

где

${\begin{alignedat}{3}&f^{+}(x)&&{}={}\max\{f(x),0\}&&{}={}{\begin{cases}f(x),&{\text{if }}f(x)>0,\\0,&{\text{otherwise,}}\end{cases}}\\&f^{-}(x)&&{}={}\max\{-f(x),0\}&&{}={}{\begin{cases}-f(x),&{\text{if }}f(x)<0,\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}$

Другие интегралы

Хотя интегралы Римана и Лебега являются наиболее широко используемыми определениями интеграла, существует ряд других, в том числе:

• Интеграл Дарбу , который определяется суммами Дарбу (ограниченными суммами Римана), но при этом эквивалентен интегралу Римана . Функция интегрируема по Дарбу тогда и только тогда, когда она интегрируема по Риману. Преимущество интегралов Дарбу состоит в том, что их легче определить, чем интегралы Римана.
• Интеграл Римана -Стилтьеса , расширение интеграла Римана, которое интегрируется по функции, а не по переменной.
• Интеграл Лебега -Стилтьеса , далее развитый Иоганном Радоном , который обобщает как интегралы Римана-Стилтьеса, так и интегралы Лебега.
• Интеграл Даниэля , который включает в себя интеграл Лебега и интеграл Лебега–Стилтьеса, не зависящий от мер .
• Интеграл Хаара , используемый для интегрирования на локально компактных топологических группах, введенный Альфредом Хааром в 1933 году.
• Интеграл Хенстока -Курцвейла , по-разному определенный Арно Данжуа , Оскаром Перроном и (наиболее элегантно, как калибровочный интеграл) Ярославом Курцвейлом , и разработанный Ральфом Хенстоком .
• и Интеграл Ито интеграл Стратоновича , которые определяют интегрирование по отношению к семимартингалам, таким как броуновское движение .
• Интеграл Юнга , который является разновидностью интеграла Римана–Стилтьеса относительно некоторых функций неограниченной вариации .
• Интеграл по грубому пути , который определен для функций, оснащенных некоторой дополнительной структурой «грубого пути», и обобщает стохастическое интегрирование как против семимартингалов , так и против таких процессов, как дробное броуновское движение .
• — Интеграл Шоке субаддитивный или супераддитивный интеграл, созданный французским математиком Гюставом Шоке в 1953 году.
• , Интеграл Бохнера расширение интеграла Лебега на более общий класс функций, а именно функции, область определения которых является банаховым пространством .

Свойства

Линейность

Совокупность интегрируемых по Риману функций на отрезке [ a , b ] образует векторное пространство относительно операций поточечного сложения и умножения на скаляр, а также операции интегрирования

$f\mapsto \int _{a}^{b}f(x)\;dx$

является линейным функционалом в этом векторном пространстве. Таким образом, совокупность интегрируемых функций замкнута при взятии линейных комбинаций , а интеграл от линейной комбинации является линейной комбинацией интегралов:

$\int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,$

Аналогично, множество вещественнозначных функций, интегрируемых по Лебегу, на заданном пространстве с мерой E с мерой µ замкнуто относительно линейных комбинаций и, следовательно, образует векторное пространство, а интеграл Лебега

$f\mapsto \int _{E}f\,d\mu$

является линейным функционалом в этом векторном пространстве, так что:

$\int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu .$

рассмотрим векторное пространство всех измеримых функций на пространстве меры ( E , µ ) , принимающих значения в локально компактном полном топологическом векторном пространстве V над локально компактным топологическим полем K , f : E → V. В более общем смысле , Тогда можно определить абстрактную карту интегрирования, назначив каждой функции f элемент V или символ ∞ ,

$f\mapsto \int _{E}f\,d\mu ,\,$

которое совместимо с линейными комбинациями. В этой ситуации линейность сохраняется для подпространства функций, интеграл которых является элементом V (т.е. «конечным»). Наиболее важные частные случаи возникают, когда K — это R , C или конечное расширение поля Q _p p - адических чисел , а V — конечномерное векторное пространство над K , и когда K = C и V — комплекс Гильбертово пространство .

Линейность вместе с некоторыми естественными свойствами непрерывности и нормировкой для определенного класса «простых» функций может быть использована для альтернативного определения интеграла. Это подход Дэниела для случая вещественных функций на множестве X , обобщенный Николя Бурбаки на функции со значениями в локально компактном топологическом векторном пространстве. См. Хильдебрандт 1953 для аксиоматической характеристики интеграла.

Неравенства

Ряд общих неравенств справедлив для функций , интегрируемых по Риману, определенных на замкнутом и ограниченном интервале [ a , b ] , и могут быть обобщены на другие понятия интеграла (Лебег и Даниэль).

• Верхняя и нижняя границы. Интегрируемая функция f на [ a , b ] обязательно ограничена на этом интервале. Таким образом, существуют действительные числа m и M , так что m ≤ f ( x ) ≤ M для всех x в [ a , b ] . Поскольку нижняя и верхняя суммы f по [ a , b ] ограничены соответственно m ( b - a ) и M ( b - a ) , отсюда следует, что
  $$m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).$$
• Неравенства между функциями. Если f ( x ) ≤ g ( x ) для каждого x в [ a , b ] , то каждая из верхней и нижней сумм f ограничена сверху верхней и нижней суммами соответственно g . Таким образом
  $$\int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.$$
  Это обобщение приведенных выше неравенств, поскольку M ( b − a ) — интеграл постоянной функции со значением M по [ a , b ] . При этом если неравенство между функциями строгое, то и неравенство между интегралами тоже строгое. То есть, если f ( x ) < g ( x ) для каждого x в [ a , b ] , то
  $$\int _{a}^{b}f(x)\,dx<\int _{a}^{b}g(x)\,dx.$$
• Подинтервалы. Если [ c , d ] является подинтервалом [ a , b ] и f ( x ) неотрицательен для всех x , затем
  $$\int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.$$
• Произведения и абсолютные значения функций. Если f и g — две функции, то мы можем рассмотреть их поточечные произведения и степени, а также абсолютные значения :
  $$(fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.$$
  Если f интегрируемо по Риману на [ a , b ] , то то же самое верно и для | ж | , и
  $$\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.$$
  Более того, если f и g оба интегрируемы по Риману, то fg также интегрируем по Риману, и
  $$\left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).$$
  Это неравенство, известное как неравенство Коши-Шварца , играет заметную роль в теории гильбертова пространства , где левая часть интерпретируется как скалярное произведение двух интегрируемых с квадратом функций f и g на интервале [ a , b ] .
• Неравенство Гёльдера . Предположим, что p и q — два действительных числа, 1 ≤ p , q ≤ ∞, причем 1 / п + 1 / q = 1 , а f и g — две функции, интегрируемые по Риману. Тогда функции | ж | ^п и | г | ^д также интегрируемы и имеет место неравенство Гёльдера :
  $$\left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.$$
  При p = q = 2 неравенство Гельдера становится неравенством Коши – Шварца.
• Неравенство Минковского . Предположим, что p ≥ 1 — действительное число, а f и g — функции, интегрируемые по Риману. Тогда | ж | ^п , | г | ^п и | ж + г | ^п также интегрируемы по Риману и имеет место неравенство Минковского :
  $$\left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.$$
  Аналог этого неравенства для интеграла Лебега используется при построении L ^п пространства .

Соглашения

В этом разделе f — вещественная , интегрируемая по Риману функция . Интеграл

$\int _{a}^{b}f(x)\,dx$

на интервале [ a , b ] определяется, если a < b . Это означает, что верхняя и нижняя суммы функции f вычисляются на разбиении a = x ₀ ≤ x ₁ ≤ . . . ≤ x _n = b , значения x _i которого возрастают. Геометрически это означает, что интегрирование происходит «слева направо», оценивая f внутри интервалов [ x _i , x _{i +1} ] , где интервал с более высоким индексом лежит справа от интервала с более низким индексом. Значения a и b конечные точки интервала , называются пределами интегрирования f , . Интегралы также могут быть определены, если a > b :

$\int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.$

При a = b это означает:

$\int _{a}^{a}f(x)\,dx=0.$

Первое соглашение необходимо при рассмотрении интегралов по подинтервалам [ a , b ] ; второй говорит, что интеграл, взятый по вырожденному интервалу или точке , должен быть равен нулю . Одна из причин первого соглашения заключается в том, что интегрируемость f на интервале [ a , b ] подразумевает, что f интегрируема на любом подинтервале [ c , d ] интегралы обладают свойством, что если c является любым элементом a [ , но, в частности , , b ] , тогда:

$\int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.$

При первом соглашении полученное соотношение

${\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}$

тогда корректно определено для любой циклической перестановки a , b и c .

Основная теорема исчисления

Основная статья: Основная теорема исчисления

Фундаментальной теоремой исчисления является утверждение, что дифференцирование и интегрирование являются обратными операциями: если непрерывную функцию сначала интегрировать, а затем дифференцировать, получается исходная функция. Важное следствие, иногда называемое второй фундаментальной теоремой исчисления , позволяет вычислять интегралы, используя первообразную интегрируемой функции.

Первая теорема

Пусть f — непрерывная вещественная функция, определенная на замкнутом интервале [ a , b ] . Пусть F — функция, определенная для всех x в [ a , b ] формулой

$F(x)=\int _{a}^{x}f(t)\,dt.$

Тогда F непрерывен на [ a , b ] , дифференцируем на открытом интервале ( a , b ) и

$F'(x)=f(x)$

для всех x в ( a , b ) .

Вторая теорема

Пусть f — вещественная функция, определенная на замкнутом интервале [ a , b ], которая допускает первообразную F на [ a , b ] . То есть f и F что для всех x в [ a , b ] — такие функции ,

$f(x)=F'(x).$

Если f интегрируемо на [ a , b ] , то

$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

Расширения

Несобственные интегралы

Основная статья: Несобственный интеграл

Несобственный интеграл $\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi$ имеет неограниченные интервалы как для домена, так и для диапазона.

«Правильный» интеграл Римана предполагает, что подынтегральная функция определена и конечна на замкнутом и ограниченном интервале, заключенном в пределы интегрирования. Несобственный интеграл возникает, когда одно или несколько из этих условий не выполняются. В некоторых случаях такие интегралы можно определить, рассматривая собственных интегралов предел последовательности Римана на все больших интервалах.

Если интервал неограничен, например, на верхнем конце, то несобственный интеграл является пределом, поскольку эта конечная точка стремится к бесконечности:

$\int _{a}^{\infty }f(x)\,dx=\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx.$

Если подынтегральная функция определена или конечна только на полуоткрытом интервале, например ( a , b ] , то предел снова может дать конечный результат:

$\int _{a}^{b}f(x)\,dx=\lim _{\varepsilon \to 0}\int _{a+\epsilon }^{b}f(x)\,dx.$

То есть несобственный интеграл является пределом правильных интегралов, когда одна конечная точка интервала интегрирования приближается либо к указанному действительному числу , либо к ∞ , либо к −∞ . В более сложных случаях ограничения требуются в обеих конечных точках или во внутренних точках.

Множественная интеграция

Основная статья: Кратный интеграл

Двойной интеграл вычисляет объем под поверхностью $z=f(x,y)$

Подобно тому, как определенный интеграл положительной функции одной переменной представляет собой площадь области между графиком функции и осью x , двойной интеграл положительной функции двух переменных представляет собой объем области между поверхностью, определенной функцией и плоскостью, содержащей ее область определения. Например, функция в двух измерениях зависит от двух действительных переменных, x и y , и интеграла функции f по прямоугольнику R , заданного как декартово произведение двух интервалов. $R=[a,b]\times [c,d]$ можно написать

$\int _{R}f(x,y)\,dA$

где дифференциал dA указывает, что интегрирование производится по площади. Этот двойной интеграл может быть определен с использованием сумм Римана и представляет собой (со знаком) объем под графиком z = f ( x , y ) в области R . При подходящих условиях (например, если f непрерывен) теорема Фубини утверждает, что этот интеграл может быть выражен как эквивалентный повторный интеграл

$\int _{a}^{b}\left[\int _{c}^{d}f(x,y)\,dy\right]\,dx.$

Это сводит задачу вычисления двойного интеграла к вычислению одномерных интегралов. По этой причине в другом обозначении интеграла по R используется знак двойного интеграла:

$\iint _{R}f(x,y)\,dA.$

Возможна интеграция в более общих областях. Интеграл от функции f по объёму по - мерной области D n $\mathbb {R} ^{n}$ обозначается такими символами, как:

$\int _{D}f(\mathbf {x} )d^{n}\mathbf {x} \ =\int _{D}f\,dV.$

Линейные и поверхностные интегралы

Основные статьи: Линейный интеграл и Поверхностный интеграл

Линейный интеграл суммирует элементы вдоль кривой.

Понятие интеграла можно распространить на более общие области интегрирования, такие как изогнутые линии и поверхности внутри многомерных пространств. Такие интегралы известны как линейные и поверхностные интегралы соответственно. Они имеют важные приложения в физике, например, при работе с векторными полями .

Линейный интеграл (иногда называемый интегралом по путям ) — это интеграл, в котором функция интегрируемая вычисляется вдоль кривой . Используются различные линейные интегралы. В случае замкнутой кривой его еще называют контурным интегралом .

Интегрируемая функция может быть скалярным полем или векторным полем . Значение линейного интеграла представляет собой сумму значений поля во всех точках кривой, взвешенную некоторой скалярной функцией на кривой (обычно длиной дуги или, для векторного поля, скалярным произведением векторного поля с дифференциалом вектор на кривой). Это взвешивание отличает линейный интеграл от более простых интегралов, определенных на интервалах . Многие простые формулы в физике имеют естественные непрерывные аналоги в виде линейных интегралов; например, тот факт, что , умноженной на перемещение работа равна силе F s , может быть выражен (в терминах векторных величин) как:

$W=\mathbf {F} \cdot \mathbf {s} .$

Для объекта, движущегося по пути C в векторном поле F, таком как электрическое поле или гравитационное поле , полная работа, совершаемая полем над объектом, получается путем суммирования дифференциальной работы, совершаемой при движении от s до s + d s. . Это дает линейный интеграл

$W=\int _{C}\mathbf {F} \cdot d\mathbf {s} .$

Определение поверхностного интеграла основано на разбиении поверхности на небольшие поверхностные элементы.

Поверхностный интеграл обобщает двойные интегралы на интегрирование по поверхности (которая может быть искривленным множеством в пространстве ); его можно рассматривать как двойной интеграл, аналог линейного интеграла . Интегрируемая функция может быть скалярным полем или векторным полем . Значение поверхностного интеграла представляет собой сумму поля во всех точках поверхности. Этого можно достичь путем разбиения поверхности на элементы поверхности, которые обеспечивают разбиение сумм Римана.

В качестве примера применения поверхностных интегралов рассмотрим векторное поле v на поверхности S ; то есть для каждой точки x в S v ( является x ) вектором. Представьте, что жидкость течет через S , так что v ( x ) определяет скорость жидкости в точке x . Поток S определяется как количество жидкости, протекающей через за единицу времени. Чтобы найти поток, нужно взять произведение скалярное v с единичной поверхностью, нормальной к S в каждой точке, что даст скалярное поле, интегрируемое по поверхности:

$\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }.$

Поток жидкости в этом примере может происходить из физической жидкости, такой как вода или воздух, или из электрического или магнитного потока. поверхностные интегралы имеют приложения в физике, особенно в классической теории электромагнетизма Таким образом , .

Контурные интегралы

Основная статья: Контурная интеграция

В комплексном анализе подынтегральная функция представляет собой комплексную функцию комплексной переменной z вместо действительной функции действительной переменной x . Когда комплексная функция интегрируется по кривой $\gamma$ в комплексной плоскости интеграл обозначается следующим образом

$\int _{\gamma }f(z)\,dz.$

Это известно как контурный интеграл .

Интегралы дифференциальных форм

Основная статья: Дифференциальная форма

См. Также: Форма объема и плотность на коллекторе.

Дифференциальная форма — математическое понятие в области исчисления многих переменных , дифференциальной топологии и тензоров . Дифференциальные формы организованы по степеням. Например, одноформа представляет собой взвешенную сумму дифференциалов координат, таких как:

$E(x,y,z)\,dx+F(x,y,z)\,dy+G(x,y,z)\,dz$

где E , F , G — функции в трех измерениях. Дифференциальную одну форму можно проинтегрировать по ориентированному пути, и полученный интеграл — это просто еще один способ записи линейного интеграла. Здесь основные дифференциалы dx , dy , dz измеряют бесконечно малые ориентированные длины, параллельные трем координатным осям.

Дифференциальная двуформа представляет собой сумму вида

$G(x,y,z)\,dx\wedge dy+E(x,y,z)\,dy\wedge dz+F(x,y,z)\,dz\wedge dx.$

Здесь основные две формы $dx\wedge dy,dz\wedge dx,dy\wedge dz$Измерьте ориентированные области, параллельные двум координатным плоскостям. Символ $\wedge$обозначает произведение клина , которое аналогично векторному произведению в том смысле, что произведение клина двух форм, представляющих ориентированные длины, представляет собой ориентированную область. Двуформу можно проинтегрировать по ориентированной поверхности, и полученный интеграл эквивалентен поверхностному интегралу, дающему поток $E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$.

В отличие от векторного произведения и трехмерного векторного исчисления, клиновое произведение и исчисление дифференциальных форм имеют смысл в произвольной размерности и на более общих многообразиях (кривые, поверхности и их многомерные аналоги). Внешняя производная играет роль градиента и ротора векторного исчисления, а теорема Стокса одновременно обобщает три теоремы векторного исчисления: теорему о дивергенции , теорему Грина и теорему Кельвина-Стокса .

Суммы

Основная статья: Суммирование § Приближение определенными интегралами

Дискретным эквивалентом интегрирования является суммирование . Суммирование и интегралы можно положить на одну и ту же основу, используя теорию интегралов Лебега или исчисление в масштабе времени .

Функциональные интегралы

Основная статья: Функциональная интеграция

Интегрирование, которое производится не по переменной (или, в физике, по измерению пространства или времени), а по пространству функций , называется функциональным интегралом .

Приложения

Интегралы широко используются во многих областях. Например, в теории вероятностей интегралы используются для определения вероятности попадания некоторой случайной величины в определенный диапазон. Более того, интеграл под всей функцией плотности вероятности должен равняться 1, что позволяет проверить, может ли функция без отрицательных значений быть функцией плотности или нет.

Интегралы можно использовать для вычисления площади двумерной области с изогнутой границей, а также для вычисления объема трехмерного объекта с изогнутой границей. Площадь двумерной области можно вычислить с помощью вышеупомянутого определенного интеграла. Объем трехмерного объекта, такого как диск или шайба, можно вычислить путем интегрирования диска , используя уравнение для объема цилиндра: $\pi r^{2}h$, где $r$это радиус. В случае простого диска, созданного путем вращения кривой вокруг оси x , радиус определяется f ( x ) , а его высота — дифференциалом dx . Используя интеграл с границами a и b , объем диска равен:

$$\pi \int _{a}^{b}f^{2}(x)\,dx.$$

Интегралы также используются в физике, в таких областях, как кинематика, для определения таких величин, как смещение , время и скорость . Например, при прямолинейном движении перемещение объекта за интервал времени $[a,b]$ дан кем-то

$x(b)-x(a)=\int _{a}^{b}v(t)\,dt,$

где $v(t)$ скорость, выраженная как функция времени. Работа, совершенная силой $F(x)$ (задается как функция положения) от исходного положения $A$ в конечное положение $B$ является:

$W_{A\rightarrow B}=\int _{A}^{B}F(x)\,dx.$

Интегралы также используются в термодинамике , где термодинамическое интегрирование используется для расчета разницы свободной энергии между двумя заданными состояниями.

Вычисление

Аналитический

Самый простой метод вычисления определенных интегралов от одной действительной переменной основан на фундаментальной теореме исчисления . Пусть f ( x ) будет функцией x , которую нужно проинтегрировать по заданному интервалу [ a , b ] . Затем найдите первообразную f ; то есть функция F такая, что F ′ = f на интервале. При условии, что подынтегральная функция и интеграл не имеют особенностей на пути интегрирования, согласно основной теореме исчисления:

$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

Иногда необходимо использовать один из многих методов, разработанных для вычисления интегралов. Большинство из этих методов переписывают один интеграл как другой, что, мы надеемся, более удобно. Методы включают интегрирование подстановкой , интегрирование по частям , интегрирование тригонометрической заменой и интегрирование частичными дробями .

Существуют альтернативные методы для вычисления более сложных интегралов. Многие неэлементарные интегралы можно разложить в ряд Тейлора и проинтегрировать почленно. Иногда полученный бесконечный ряд можно просуммировать аналитически. Также можно использовать метод свертки с использованием G-функций Мейера , предполагая, что подынтегральная функция может быть записана как произведение G-функций Мейера. Есть также много менее распространенных способов вычисления определенных интегралов; например, тождество Парсеваля можно использовать для преобразования интеграла по прямоугольной области в бесконечную сумму. Иногда интеграл можно вычислить с помощью хитрости; пример этого см. в разделе «Интеграл Гаусса» .

Вычисления объемов тел вращения обычно можно выполнить с помощью интеграции дисков или оболочек .

Конкретные результаты, полученные различными методами, собраны в списке интегралов .

Символический

Основная статья: Символическая интеграция

Многие задачи в математике, физике и технике связаны с интегрированием, когда требуется явная формула для интеграла. обширные таблицы интегралов Для этой цели на протяжении многих лет были составлены и опубликованы . С распространением компьютеров многие специалисты, преподаватели и студенты обратились к системам компьютерной алгебры , специально разработанным для выполнения сложных или утомительных задач, включая интеграцию. Символическая интеграция была одной из причин разработки первых таких систем, таких как Macsyma и Maple .

Основная математическая трудность при символьном интегрировании заключается в том, что во многих случаях относительно простая функция не имеет интегралов, которые можно было бы выразить в замкнутой форме с использованием только элементарных функций , включая рациональные и показательные функции, логарифмы , тригонометрические функции и обратные тригонометрические функции , а также операции умножения и композиции. Алгоритм Риша предоставляет общий критерий для определения того, является ли первообразная элементарной функции элементарной, и для вычисления интеграла, если он элементарен. Однако функции с замкнутыми выражениями первообразных являются исключением, и, следовательно, системы компьютеризированной алгебры не имеют надежды найти первообразную для случайно построенной элементарной функции. Положительным моментом является то, что если «строительные блоки» первообразных определены заранее, все равно можно решить, можно ли выразить первообразную данной функции с использованием этих блоков и операций умножения и композиции, и найти символический ответ. всякий раз, когда он существует. Алгоритм Риша, реализованный в Mathematica , Maple и другие системы компьютерной алгебры делают именно это для функций и первообразных, построенных из рациональных функций, радикалов , логарифмов и показательных функций.

Некоторые специальные подынтегральные выражения встречаются достаточно часто, чтобы требовать специального изучения. В частности, может быть полезно иметь в наборе первообразных специальные функции (такие как функции Лежандра , гипергеометрическая функция , гамма-функция , неполная гамма-функция и т. д.). Расширение алгоритма Риша для включения таких функций возможно, но сложно и является предметом активных исследований.

Совсем недавно появился новый подход, использующий D -конечные функции , которые являются решениями линейных дифференциальных уравнений с полиномиальными коэффициентами. Большинство элементарных и специальных функций являются D -конечными, а интеграл от D -конечной функции также является D -конечной функцией. Это обеспечивает алгоритм выражения первообразной D -конечной функции как решения дифференциального уравнения. Эта теория также позволяет вычислить определенный интеграл D -функции как сумму ряда, заданного первыми коэффициентами, и предоставляет алгоритм вычисления любого коэффициента.

Системы интеграции на основе правил облегчают интеграцию. Rubi, интегратор на основе правил системы компьютерной алгебры, шаблон соответствует обширной системе правил символической интеграции для интеграции широкого спектра подынтегральных выражений. Эта система использует более 6600 правил интегрирования для вычисления интегралов. Метод скобок представляет собой обобщение основной теоремы Рамануджана, которое можно применять к широкому кругу одномерных и многомерных интегралов. Для определения интеграла к коэффициентам и экспоненциальным членам разложения в степенной ряд подынтегрального выражения применяется набор правил. Метод тесно связан с преобразованием Меллина .

Числовой

Основная статья: Численное интегрирование

Численные квадратурные методы: метод прямоугольника, правило трапеций, метод Ромберга, квадратура Гаусса.

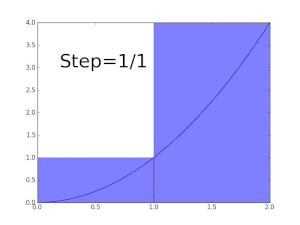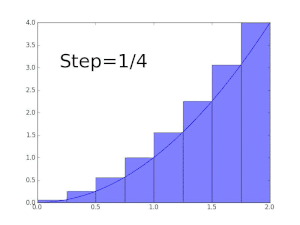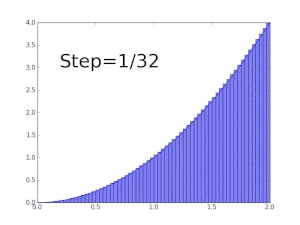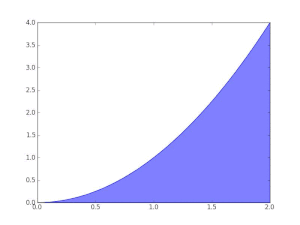
Определенные интегралы можно аппроксимировать с помощью нескольких методов численного интегрирования . Метод прямоугольников основан на разделении области под функцией на ряд прямоугольников, соответствующих значениям функции, и умножении на ширину шага для нахождения суммы. Лучший подход — правило трапеций — заменяет прямоугольники, используемые в сумме Римана, трапециями. Правило трапеций взвешивает первое и последнее значения пополам, а затем умножает их на ширину шага, чтобы получить лучшее приближение. Идею, лежащую в основе правила трапеций, о том, что более точные приближения к функции приводят к лучшим приближениям к интегралу, можно развивать дальше: правило Симпсона аппроксимирует подынтегральную функцию кусочно-квадратичной функцией.

Суммы Римана, правило трапеций и правило Симпсона являются примерами семейства квадратурных правил, называемых формулами Ньютона-Котеса . Правило квадратур Ньютона – Котеса степени n аппроксимирует полином на каждом подинтервале полиномом степени n . Этот полином выбран для интерполяции значений функции на интервале. Приближения Ньютона-Котеса более высокой степени могут быть более точными, но они требуют большего количества оценок функций и могут страдать от численной неточности из-за феномена Рунге . Одним из решений этой проблемы является квадратура Кленшоу–Кертиса , в которой подынтегральная функция аппроксимируется путем ее разложения по полиномам Чебышева .

Метод Ромберга постепенно уменьшает ширину шага вдвое, давая аппроксимации трапеции, обозначаемые T ( h ₀ ) , T ( h ₁ ) и т. д., где h _{k +1} — половина h _k . Для каждого нового размера шага необходимо вычислить только половину новых значений функции; остальные переходят из предыдущего размера. Затем он интерполирует полином через аппроксимации и экстраполирует его на T (0) . Гауссова квадратура оценивает функцию в корнях набора ортогональных многочленов . -точечный метод n Гаусса точен для полиномов степени до 2 n − 1 .

При вычислении интегралов более высокой размерности (например, при расчете объема) важно использовать такие альтернативы, как интегрирование Монте-Карло .

Механический

Площадь произвольной двумерной формы можно определить с помощью измерительного прибора, называемого планиметром . Объем объектов неправильной формы можно точно измерить с помощью жидкости, вытесняемой при погружении объекта.

Геометрический

Основная статья: Квадратура (математика)

Иногда площадь можно найти с помощью геометрических построений циркуля и линейки эквивалентного квадрата .

Интеграция путем дифференциации

Кемпф, Джексон и Моралес продемонстрировали математические соотношения, позволяющие вычислять интеграл посредством дифференцирования . Их исчисление включает дельта-функцию Дирака и частной производной. оператор $\partial _{x}$. Это также можно применить к функциональным интегралам , позволяя вычислять их путем функционального дифференцирования .

Примеры

Использование фундаментальной теоремы исчисления

Фундаментальная теорема исчисления позволяет выполнять простые вычисления основных функций:

$\int _{0}^{\pi }\sin(x)\,dx=-\cos(x){\big |}_{x=0}^{x=\pi }=-\cos(\pi )-{\big (}-\cos(0){\big )}=2.$

См. также

• Интегральное уравнение - Уравнения с неизвестной функцией под знаком интеграла.
• Символ интеграла - математический символ, используемый для обозначения интегралов и первообразных.
• Списки интегралов

Библиография

• Антон, Ховард; Бивенс, Ирландия К.; Дэвис, Стивен (2016), Исчисление: ранние трансценденталии (11-е изд.), John Wiley & Sons, ISBN  978-1-118-88382-2
• Апостол, Том М. (1967), Исчисление, Том. 1: Исчисление с одной переменной и введение в линейную алгебру (2-е изд.), Wiley, ISBN  978-0-471-00005-1
• Бурбаки, Николя (2004), Интеграция I , Springer-Verlag, ISBN  3-540-41129-1 . В частности главы III и IV.
• Бертон, Дэвид М. (2011), История математики: введение (7-е изд.), McGraw-Hill, ISBN  978-0-07-338315-6
• Каджори, Флориан (1929), История математических обозначений, том II , Open Court Publishing, ISBN  978-0-486-67766-8
• Далквист, Гермунд ; Бьорк, Оке (2008), «Глава 5: Численное интегрирование» , Численные методы в научных вычислениях, Том I , Филадельфия: SIAM , заархивировано из оригинала 15 июня 2007 г.
• Феллер, Уильям (1966), Введение в теорию вероятностей и ее приложения , John Wiley & Sons.
• Фолланд, Джеральд Б. (1999), Реальный анализ: современные методы и их применение (2-е изд.), John Wiley & Sons, ISBN  0-471-31716-0
• Фурье, Жан Батист Жозеф (1822), Аналитическая теория тепла , Chez Firmin Didot, отец и сын, с. §231
  Доступен в переводе как Фурье, Джозеф (1878), Аналитическая теория тепла , Фриман, Александр (пер.), Cambridge University Press, стр. 200–201.
• Гонсалес, Иван; Цзю, Линь; Молл, Виктор Х. (1 января 2020 г.), «Расширение метода скобок. Часть 2», Open Mathematics , 18 (1): 983–995, arXiv : 1707.08942 , doi : 10.1515/math-2020-0062 , ISSN   2391-5455 , S2CID   222004668
• Хит, TL , изд. (2002), Работы Архимеда , Дувр, ISBN  978-0-486-42084-4
  (Первоначально опубликовано издательством Кембриджского университета в 1897 году на основе греческой версии Дж. Л. Хейберга.)
• Хильдебрандт, TH (1953), «Интегрирование в абстрактных пространствах» , Бюллетень Американского математического общества , 59 (2): 111–139, doi : 10.1090/S0002-9904-1953-09694-X , ISSN   0273-0979
• Каханер, Дэвид; Молер, Клив ; Нэш, Стивен (1989), «Глава 5: Числовая квадратура», Численные методы и программное обеспечение , Прентис Холл, ISBN  978-0-13-627258-8
• Каллио, Брюс Виктор (1966), История определенного интеграла (PDF) (магистерская диссертация), Университет Британской Колумбии, заархивировано из оригинала 05 марта 2014 г. , получено 28 февраля 2014 г.
• Кац, Виктор Дж. (2009), История математики: введение , Аддисон-Уэсли , ISBN  978-0-321-38700-4
• Кемпф, Ахим; Джексон, Дэвид М.; Моралес, Алехандро Х. (2015), «Как (путем) интегрировать путем дифференцирования», Journal of Physics: Conference Series , 626 (1), IOP Publishing : 012015, arXiv : 1507.04348 , Bibcode : 2015JPhCS.626a2015K , doi : 10.1088/1742-6596/626/1/012015 , S2CID   119642596
• Кранц, Стивен Г. (1991), Реальный анализ и основы , CRC Press, ISBN  0-8493-7156-2
• Лейбниц, Готфрид Вильгельм (1899), Герхардт, Карл Иммануил (редактор), переписка Готфрида Вильгельма Лейбница с математиками. Первый том , Берлин: Майер и Мюллер.
• Либ, Эллиотт ; Лосс, Майкл (2001), Анализ , Аспирантура по математике , том. 14 (2-е изд.), Американское математическое общество , ISBN.  978-0821827833
• Монтесинос, Винсент; Зизлер, Питер; Зизлер, Вацлав (2015), Введение в современный анализ (иллюстрированное издание), Springer, ISBN  978-3-319-12481-0
• Рич, Альберт; Шайбе, Патрик; Аббаси, Насер (16 декабря 2018 г.), «Интеграция на основе правил: обширная система правил символической интеграции», Journal of Open Source Software , 3 (32): 1073, Bibcode : 2018JOSS....3.1073R , doi : 10.21105 /joss.01073 , S2CID   56487062
• Рудин, Уолтер (1987), «Глава 1: Абстрактная интеграция», Реальный и комплексный анализ (международное издание), McGraw-Hill, ISBN  978-0-07-100276-9
• Сакс, Станислав (1964), Теория интеграла (английский перевод Л. К. Янга. С двумя дополнительными примечаниями Стефана Банаха. Второе исправленное издание), Нью-Йорк: Дувр
• Зигмунд-Шульце, Рейнхард (2008), «Анри Лебег», Тимоти Гауэрс; Джун Барроу-Грин; Имре Лидер (ред.), Princeton Companion to Mathematics , Princeton University Press, ISBN  978-0-691-11880-2 .
• Стиллвелл, Джон (1989), Математика и ее история , Springer, ISBN  0-387-96981-0
• Стер, Йозеф ; Булирш, Роланд (2002), «Темы интеграции», Введение в численный анализ (3-е изд.), Springer, ISBN  978-0-387-95452-3 .
• Струйк, Дирк Ян , изд. (1986), Справочник по математике, 1200–1800 гг. , Принстон, Нью-Джерси: Princeton University Press, ISBN  0-691-08404-1
• «Арабская математическая нотация» , W3C , 2006 г.

Внешние ссылки

• «Интеграл» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Интегральный онлайн-калькулятор , Wolfram Alpha .

Интернет-книги

• Кейслер, Х. Джером, Элементарное исчисление: подход с использованием бесконечно малых , Университет Висконсина.
• Строян, К.Д., Краткое введение в исчисление бесконечно малых , Университет Айовы.
• Маух, Шон, Книга Шона по прикладной математике , CIT, онлайн-учебник, включающий полное введение в исчисление.
• Кроуэлл, Бенджамин, Исчисление , Фуллертонский колледж, онлайн-учебник.
• Гаррет, Пол, Заметки по математическому анализу для первокурсников
• Хуссейн, Фараз, «Понимание исчисления» , онлайн-учебник
• Джонсон, Уильям Вулси (1909) «Элементарный трактат по интегральному исчислению» , ссылка с сайта HathiTrust .
• Ковальк, В.П., Теория интеграции , Ольденбургский университет. Новая концепция старой проблемы. Онлайн учебник
• Слотер, Дэн, От разностных уравнений к дифференциальным уравнениям , введение в исчисление
• Численные методы интегрирования в Институте целостных численных методов
• П.С. Ван, Оценка определенных интегралов с помощью символических манипуляций (1972) - кулинарная книга методов определенных интегралов