Симметричная убывающая перестановка

В математике симметричная убывающая перестановка функции — это функция, которая является симметричной и убывающей, множества уровней которой имеют тот же размер, что и исходная функция.

Определение наборов

Учитывая измеримое множество , $A,$ в $\mathbb {R} ^{n},$ определяют симметричную перестановку $A,$ называется $A^{*},$ как шар с центром в начале координат, объем которого ( мера Лебега ) такой же, как и у множества $A.$

Эквивалентное определение

$$A^{*}=\left\{x\in \mathbb {R} ^{n}:\,\omega _{n}\cdot |x|^{n}<|A|\right\},$$

где $\omega _{n}$ - объем единичного шара и где $|A|$ это объем $A.$

Определение функций

Перестановка неотрицательной измеримой действительной функции. $f$ чей уровень устанавливает $f^{-1}(y)$ (для $y\in \mathbb {R} _{\geq 0}$) имеют конечную меру

$$f^{*}(x)=\int _{0}^{\infty }\mathbb {I} _{\{y:f(y)>t\}^{*}}(x)\,dt,$$

где $\mathbb {I} _{A}$ обозначает индикаторную функцию множества $A.$ На словах ценность $f^{*}(x)$ дает высоту $t$ для которого радиус симметричногоперестановка $\{y:f(y)>t\}$ равно $x.$ У нас есть следующая мотивация для этого определения. Потому что личность

$$g(x)=\int _{0}^{\infty }\mathbb {I} _{\{y:g(y)>t\}}(x)\,dt,$$

справедливо для любой неотрицательной функции $g,$ приведенное выше определение является уникальным определением, которое заставляет идентичность $\mathbb {I} _{A}^{*}=\mathbb {I} _{A^{*}}$ держать.

Свойства

Функция и ее симметрично убывающая перестановка сохраняют меру множеств уровня.

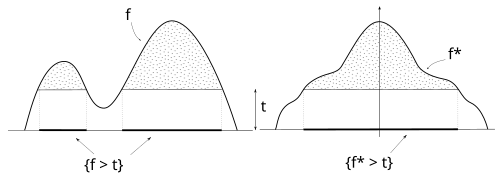
Функция $f^{*}$ — симметричная и убывающая функция, множества уровня которой имеют ту же меру, что и множества уровня $f,$ то есть,

$$|\{x:f^{*}(x)>t\}|=|\{x:f(x)>t\}|.$$

Если $f$ это функция в $L^{p},$ затем

$$\|f\|_{L^{p}}=\|f^{*}\|_{L^{p}}.$$

Выполняется неравенство Харди –Литтлвуда , т.е.

$$\int fg\leq \int f^{*}g^{*}.$$

Далее, справедливо неравенство Пойа–Сегё . Это говорит о том, что если $1\leq p<\infty$ и если $f\in W^{1,p}$ затем

$$\|\nabla f^{*}\|_{p}\leq \|\nabla f\|_{p}.$$

Симметричная убывающая перестановка сохраняет порядок и убывает. $L^{p}$ расстояние, то есть

$$f\leq g{\text{ implies }}f^{*}\leq g^{*}$$

и

$$\|f-g\|_{L^{p}}\geq \|f^{*}-g^{*}\|_{L^{p}}.$$

Приложения

Неравенство Полиа – Сегё в предельном случае дает $p=1,$ изопериметрическое неравенство . Также можно использовать некоторые соотношения с гармоническими функциями для доказательства неравенства Рэлея–Фабера–Крана .

убывающая

Мы также можем определить $f^{*}$ как функцию неотрицательных действительных чисел, а не всех $\mathbb {R} ^{n}.$ Позволять $(E,\mu )$ — σ-конечное пространство с мерой , и пусть $f:E\to [-\infty ,\infty ]$ — измеримая функция , принимающая только конечные (т. е. действительные) значения ц-а.е. (где « $\mu$-ae" означает, за исключением, возможно, набора $\mu$-измерить ноль). Определим функцию распределения $\mu _{f}:[0,\infty ]\to [0,\infty ]$ по правилу

$$\mu _{f}(s)=\mu \{x\in E:\vert f(x)\vert >s\}.$$

Теперь мы можем определить убывающую перестановку (или, иногда, невозрастающую перестановку ) $f$ как функция $f^{*}:[0,\infty )\to [0,\infty ]$ по правилу

$$f^{*}(t)=\inf\{s\in [0,\infty ]:\mu _{f}(s)\leq t\}.$$

Обратите внимание, что эта версия убывающей перестановки не является симметричной, поскольку она определена только для неотрицательных действительных чисел. Однако он наследует многие из тех же свойств, перечисленных выше, что и симметричная версия, а именно:

• $f$ и $f^{*}$ равноизмеримы , то есть имеют одинаковую функцию распределения.
• Выполняется неравенство Харди-Литтлвуда, т.е. $\int _{E}|fg|\;d\mu \leq \int _{0}^{\infty }f^{*}(t)g^{*}(t)\;dt.$
• $\vert f\vert \leq \vert g\vert$ $\mu$-ae подразумевает $f^{*}\leq g^{*}.$
• $(af)^{*}=|a|f^{*}$ для всех действительных чисел $a.$
• $(f+g)^{*}(t_{1}+t_{2})\leq f^{*}(t_{1})+g^{*}(t_{2})$ для всех $t_{1},t_{2}\in [0,\infty ).$
• $|f_{n}|\uparrow |f|$ $\mu$-ae подразумевает $f_{n}^{*}\uparrow f^{*}.$
• $\left(\vert f\vert ^{p}\right)^{*}=(f^{*})^{p}$ для всех положительных действительных чисел $p.$
• $\|f\|_{L_{p}(E)}=\|f^{*}\|_{L_{p}[0,\infty )}$ для всех положительных действительных чисел $p.$
• $\|f\|_{L_{\infty }(E)}=f^{*}(0).$

(Несимметричная) убывающая функция перестановки часто возникает в теории банаховых функциональных пространств, инвариантных к перестановке. Особенно важно следующее:

Теорема Люксембург о представлении. Позволять $\rho$ — норма банаховой функции, инвариантная к перестановкам, над резонансным пространством с мерой. $(E,\mu ).$ Тогда существует (возможно, не единственная) норма функции, инвариантная к перестановке ${\overline {\rho }}$ на $[0,\infty )$ такой, что $\rho (f)={\overline {\rho }}(f^{*})$ для всех неотрицательных измеримых функций $f:E\to [0,\infty ]$ которые имеют конечное значение $\mu$-аэ

Обратите внимание, что определения всей терминологии в приведенной выше теореме (то есть норм банаховых функций, инвариантных к перестановке банаховых функциональных пространств и пространств с резонансной мерой) можно найти в разделах 1 и 2 книги Беннета и Шарпли (ср. ссылки ниже).

См. также

• Изопериметрическое неравенство - геометрическое неравенство, которое устанавливает нижнюю границу площади поверхности множества с учетом его объема.
• Представление слоеного торта
• Неравенство Рэлея – Фабера – Крана.
• Неравенство перестановки Рисса
• Пространство Соболева - Векторное пространство функций в математике.
• Неравенство Сегё - концепция математического анализа. Страницы с краткими описаниями целей перенаправления.