Банахово пространство

В математике , точнее в функциональном анализе , банахово пространство (произносится [ˈbanax] ) является полным нормированным векторным пространством . Таким образом, банахово пространство — это векторное пространство с метрикой , которая позволяет вычислять длину вектора и расстояние между векторами и является полным в том смысле, что последовательность векторов Коши всегда сходится к четко определенному пределу , находящемуся внутри пространства.

Банаховы пространства названы в честь польского математика Стефана Банаха , который ввёл это понятие и систематически изучал его в 1920–1922 годах вместе с Гансом Ханом и Эдуардом Хелли . Морис Рене Фреше был первым, кто использовал термин «банахово пространство», а Банах, в свою очередь, затем ввел термин « пространство Фреше ». возникли в результате изучения функциональных пространств Гильбертом Фреше , Риссом и Банаховые пространства первоначально в начале века. Банаховы пространства играют центральную роль в функциональном анализе. В других областях анализа изучаемые пространства часто являются банаховыми пространствами.

Определение

Банахово пространство — полное нормированное пространство. $(X,\|\cdot \|).$ Нормированное пространство – это пара $(X,\|\cdot \|)$ состоящий из векторного пространства $X$ над скалярным полем $\mathbb {K}$ (где $\mathbb {K}$ обычно $\mathbb {R}$ или $\mathbb {C}$) вместе с выдающимся норма $\|\cdot \|:X\to \mathbb {R} .$ Как и все нормы, эта норма порождает инвариант трансляции. функция расстояния , называемая канонической или ( нормативной ) индуцированной метрикой , определенная для всех векторов $x,y\in X$ к

$$d(x,y):=\|y-x\|=\|x-y\|.$$

Это делает $X$ в метрическое пространство $(X,d).$ Последовательность $x_{1},x_{2},\ldots$ называется Коши в $(X,d)$ или $d$-Коши или $\|\cdot \|$-Коши , если для каждого реального $r>0,$ существует некоторый индекс $N$ такой, что

$$d\left(x_{n},x_{m}\right)=\left\|x_{n}-x_{m}\right\|<r$$

в любое время $m$ и $n$ больше, чем $N.$ Нормированное пространство $(X,\|\cdot \|)$ называется банаховым пространством , а каноническая метрика $d$ называется полной метрикой , если $(X,d)$ является полным метрическим пространством , что по определению означает для каждой последовательности Коши $x_{1},x_{2},\ldots$ в $(X,d),$ существует какой-то $x\in X$ такой, что

$$\lim _{n\to \infty }x_{n}=x\;{\text{ in }}(X,d)$$

где, потому что $\left\|x_{n}-x\right\|=d\left(x_{n},x\right),$ сходимость этой последовательности к $x$ эквивалентно может быть выражено как:

$$\lim _{n\to \infty }\left\|x_{n}-x\right\|=0\;{\text{ in }}\mathbb {R} .$$

Норма $\|\cdot \|$ нормированного пространства $(X,\|\cdot \|)$ называется полная норма , если $(X,\|\cdot \|)$ является банаховым пространством.

L-полувнутренний продукт

Для любого нормированного пространства $(X,\|\cdot \|),$ существует L-полуканеральный продукт $\langle \cdot ,\cdot \rangle$ на $X$ такой, что ${\textstyle \|x\|={\sqrt {\langle x,x\rangle }}}$ для всех $x\in X$; в общем случае может существовать бесконечно много L-полукачалых произведений, удовлетворяющих этому условию. L-полускалярные произведения — это обобщение скалярных произведений , которые фундаментально отличают гильбертовы пространства от всех других банаховых пространств. Это показывает, что все нормированные пространства (и, следовательно, все банаховы пространства) можно рассматривать как обобщения (пре)гильбертовых пространств.

Характеристика по сериям

Структура векторного пространства позволяет связать поведение последовательностей Коши с поведением сходящихся рядов векторов . Нормированное пространство $X$ является банаховым пространством тогда и только тогда, когда каждый абсолютно сходящийся ряд из $X$ сходится в $X,$

$$\sum _{n=1}^{\infty }\|v_{n}\|<\infty \quad {\text{ implies that }}\quad \sum _{n=1}^{\infty }v_{n}\ \ {\text{ converges in }}\ \ X.$$

Топология

Каноническая метрика $d$ нормированного пространства $(X,\|\cdot \|)$ индуцирует обычную метрическую топологию $\tau _{d}$ на $X,$которая называется канонической или нормо-индуцированной топологией . Автоматически предполагается, что каждое нормированное пространство несет эту топологию Хаусдорфа , если не указано иное. В этой топологии каждое банахово пространство является пространством Бэра , хотя существуют нормированные пространства, которые являются бэровскими, но не банаховыми. Норма $\|\,\cdot \,\|:\left(X,\tau _{d}\right)\to \mathbb {R}$ всегда является непрерывной функцией относительно топологии, которую она индуцирует.

Открытые и закрытые шары радиуса $r>0$ сосредоточен в точке $x\in X$ представляют собой соответственно множества

$$B_{r}(x):=\{z\in X:\|z-x\|<r\}\qquad {\text{ and }}\qquad C_{r}(x):=\{z\in X:\|z-x\|\leq r\}.$$

Любой такой шар является выпуклым и ограниченным подмножеством $X,$ но компактный шар/ окрестность существует тогда и только тогда, когда $X$— конечномерное векторное пространство . В частности, никакое бесконечномерное нормированное пространство не может быть локально компактным или обладать свойством Гейне–Бореля . Если $x_{0}$ является вектором и $s\neq 0$ тогда это скаляр

$$x_{0}+sB_{r}(x)=B_{|s|r}\left(x_{0}+sx\right)\qquad {\text{ and }}\qquad x_{0}+sC_{r}(x)=C_{|s|r}\left(x_{0}+sx\right).$$

С использованием $s:=1$ показывает, что эта топология, индуцированная нормой, является трансляционно-инвариантной , что означает, что для любого $x\in X$ и $S\subseteq X,$ подмножество $S$ открыт в (соответственно закрыт ) $X$ тогда и только тогда, когда это верно для его перевода $x+S:=\{x+s:s\in S\}.$Следовательно, топология, индуцированная нормой, полностью определяется любым базисом окрестности в начале координат. Некоторые распространенные базы соседства в начале координат включают:

$$\left\{B_{r}(0):r>0\right\},\qquad \left\{C_{r}(0):r>0\right\},\qquad \left\{B_{r_{n}}(0):n\in \mathbb {N} \right\},\qquad {\text{ or }}\qquad \left\{C_{r_{n}}(0):n\in \mathbb {N} \right\}$$

где $r_{1},r_{2},\ldots$ представляет собой последовательность положительных действительных чисел, которая сходится к $0$ в $\mathbb {R}$ (такой как $r_{n}:=1/n$ или $r_{n}:=1/2^{n}$например). Так, например, каждое открытое подмножество $U$ из $X$ можно записать как союз

$$U=\bigcup _{x\in I}B_{r_{x}}(x)=\bigcup _{x\in I}x+B_{r_{x}}(0)=\bigcup _{x\in I}x+r_{x}B_{1}(0)$$

индексируется некоторым подмножеством $I\subseteq U,$ где каждый $r_{x}$ может быть выбран из вышеупомянутой последовательности $r_{1},r_{2},\ldots$ (открытые шары можно заменить закрытыми, хотя тогда индексирующий набор $I$ и радиусы $r_{x}$возможно, тоже придется заменить). Кроме того, $I$ всегда можно выбрать счетным , если $X$ является сепарабельным пространством , что по определению означает, что $X$ содержит некоторое счетное плотное подмножество .

Классы гомеоморфизма сепарабельных банаховых пространств

Все конечномерные нормированные пространства являются сепарабельными банаховыми пространствами, и любые два банаховых пространства одной и той же конечной размерности линейно гомеоморфны. Каждое сепарабельное бесконечномерное гильбертово пространство линейно изометрически изоморфно сепарабельному гильбертовому пространству последовательностей. $\ell ^{2}(\mathbb {N} )$ с обычной нормой $\|\cdot \|_{2}.$

Теорема Андерсона–Кадека утверждает, что каждое бесконечномерное сепарабельное пространство Фреше гомеоморфно пространству . произведений ${\textstyle \prod _{i\in \mathbb {N} }\mathbb {R} }$ счетного числа копий $\mathbb {R}$ (этот гомеоморфизм не обязательно должен быть линейным отображением ). Таким образом, все бесконечномерные сепарабельные пространства Фреше гомеоморфны друг другу (или, другими словами, их топология единственна с точностью до гомеоморфизма). Поскольку каждое банахово пространство является пространством Фреше, это также верно для всех бесконечномерных сепарабельных банаховых пространств, включая $\ell ^{2}(\mathbb {N} ).$ Фактически, $\ell ^{2}(\mathbb {N} )$ даже гомеоморфна своей единичной сфере $\left\{x\in \ell ^{2}(\mathbb {N} ):\|x\|_{2}=1\right\},$ что резко контрастирует с конечномерными пространствами ( евклидовой плоскостью $\mathbb {R} ^{2}$ не гомеоморфен единичному кругу например, ).

Этот образец в классах гомеоморфизма распространяется на обобщения метризуемых ( локально евклидовых ) топологических многообразий , известных как метрические банаховы многообразия , которые представляют собой метрические пространства , окружающие каждую точку, локально гомеоморфные некоторому открытому подмножеству данного банахова пространства (метрические гильбертовы многообразия и метрические гильбертовы многообразия и метрические Фреше) . многообразия определяются аналогично). Например, каждое открытое подмножество $U$ банахова пространства $X$ канонически является метрическим банаховым многообразием, моделируемым по $X$ поскольку карта включения $U\to X$является открытым локальным гомеоморфизмом . гильбертова пространства Используя микрорасслоения , Дэвид Хендерсон показал в 1969 году, что каждое метрическое многообразие, смоделированное на сепарабельном бесконечномерном банаховом пространстве (или пространстве Фреше может быть топологически вложено как открытое подмножество ) , $\ell ^{2}(\mathbb {N} )$ и, следовательно, также допускает уникальную гладкую структуру, превращающую его в $C^{\infty }$ Гильбертово многообразие .

Компактные и выпуклые подмножества

Существует компактное подмножество $S$ из $\ell ^{2}(\mathbb {N} )$ чья выпуклая оболочка $\operatorname {co} (S)$ не не замкнут и, следовательно, компактен (см. сноску для примера). Однако, как и во всех банаховых пространствах, замкнутая выпуклая оболочка ${\overline {\operatorname {co} }}S$ этого (и любого другого) компактного подмножества будет компактным. Но если нормированное пространство не полно, то вообще не гарантируется, что ${\overline {\operatorname {co} }}S$ будет компактным всякий раз, когда $S$является; пример можно найти даже в (неполном) прегильбертовом векторном подпространстве $\ell ^{2}(\mathbb {N} ).$

Как топологическое векторное пространство

Эта топология, индуцированная нормами, также делает $\left(X,\tau _{d}\right)$в так называемое топологическое векторное пространство (TVS), которое по определению представляет собой векторное пространство, наделенное топологией, делающей операции сложения и скалярного умножения непрерывными. Подчеркивается, что ТВС $\left(X,\tau _{d}\right)$— это всего лишь векторное пространство с топологией определенного типа; то есть, если рассматривать его как TVS, он не связан с какой-либо конкретной нормой или показателем (оба из которых « забыты »). Это Хаусдорф ТВС $\left(X,\tau _{d}\right)$является даже локально выпуклым, поскольку множество всех открытых шаров с центром в начале координат образует базис окрестности в начале координат, состоящий из выпуклых сбалансированных открытых множеств. Эта ТВС также является нормируемой , что по определению относится к любой ТВС, топология которой индуцирована некоторой (возможно, неизвестной) нормой . Нормальные TVS характеризуются хаусдорфовой структурой и ограниченной выпуклой окрестностью начала координат. Все банаховы пространства являются бочоночными пространствами , что означает, что каждая бочка находится в окрестности начала координат (например, все замкнутые шары с центром в начале координат являются бочками) и гарантирует выполнение теоремы Банаха – Штейнхауза .

Сравнение полных метризуемых векторных топологий

Теорема об открытом отображении означает, что если $\tau$ и $\tau _{2}$ топологии на $X$ это делает оба $(X,\tau )$ и $\left(X,\tau _{2}\right)$ на полные метризуемые TVS (например, банаховые пространства или пространства Фреше ) и если одна топология тоньше или грубее другой, то они должны быть равны (т. е. если $\tau \subseteq \tau _{2}$ или $\tau _{2}\subseteq \tau$ затем $\tau =\tau _{2}$). Так, например, если $(X,p)$ и $(X,q)$ являются банаховыми пространствами с топологиями $\tau _{p}$ и $\tau _{q}$ и если в одном из этих пространств есть некоторый открытый шар, который также является открытым подмножеством другого пространства (или, что то же самое, если один из $p:\left(X,\tau _{q}\right)\to \mathbb {R}$ или $q:\left(X,\tau _{p}\right)\to \mathbb {R}$ непрерывна), то их топологии идентичны, а нормы эквивалентны .

Полнота

Полные нормы и эквивалентные нормы

Две нормы, $p$ и $q,$ в векторном пространстве $X$ называются эквивалентными, если они порождают одну и ту же топологию; это происходит тогда и только тогда, когда существуют положительные действительные числа $c,C>0$ такой, что ${\textstyle cq(x)\leq p(x)\leq Cq(x)}$ для всех $x\in X.$ Если $p$ и $q$ две эквивалентные нормы в векторном пространстве $X$ затем $(X,p)$ является банаховым пространством тогда и только тогда, когда $(X,q)$является банаховым пространством. В этой сноске приведен пример непрерывной нормы в банаховом пространстве, которая не эквивалентна заданной норме этого банахового пространства. Все нормы в конечномерном векторном пространстве эквивалентны, и каждое конечномерное нормированное пространство является банаховым пространством.

Полные нормы против полных показателей

Метрика $D$ в векторном пространстве $X$ индуцируется нормой на $X$ если и только если $D$ является ли трансляционный инвариант и абсолютно однородны , а это значит, что $D(sx,sy)=|s|D(x,y)$ для всех скаляров $s$ и все $x,y\in X,$ в этом случае функция $\|x\|:=D(x,0)$ определяет норму на $X$ и каноническая метрика, индуцированная $\|\cdot \|$ равно $D.$

Предположим, что $(X,\|\cdot \|)$ является нормированным пространством и что $\tau$ – нормальная топология, индуцированная на $X.$ Предположим, что $D$ какая -либо метрика на $X$ такая, что топология, которая $D$ вызывает $X$ равно $\tau .$ Если $D$ является ли трансляционный инвариант затем $(X,\|\cdot \|)$ является банаховым пространством тогда и только тогда, когда $(X,D)$ является полным метрическим пространством. Если $D$ является не трансляционным инвариантом, то это может быть возможно для $(X,\|\cdot \|)$ быть банаховым пространством, но для $(X,D)$ быть не полным метрическим пространством (см. эту сноску для примера). Напротив, теорема Клее которое также применимо ко всем метризуемым топологическим векторным пространствам , означает, что если существует какое-либо полная метрика $D$ на $X$ что индуцирует нормальную топологию $\tau$ на $X,$ затем $(X,\|\cdot \|)$ является банаховым пространством.

Пространство Фреше — это локально выпуклое топологическое векторное пространство, топология которого индуцирована некоторой трансляционно-инвариантной полной метрикой. Каждое банахово пространство является пространством Фреше, но не наоборот; действительно, существуют даже пространства Фреше, в которых ни одна норма не является непрерывной функцией (например, пространство действительных последовательностей ${\textstyle \mathbb {R} ^{\mathbb {N} }=\prod _{i\in \mathbb {N} }\mathbb {R} }$с топологией продукта ). Однако топология каждого пространства Фреше индуцируется некоторым счетным семейством вещественных (обязательно непрерывных) отображений, называемых полунормами , которые являются обобщениями норм . Пространство Фреше даже может иметь топологию, индуцированную счетным семейством норм (такие нормы обязательно будут непрерывными). но не быть банаховым/ нормируемым пространством , поскольку его топология не может быть определена какой-либо единственной нормой. Примером такого пространства является пространство Фреше. $C^{\infty }(K),$ определение которого можно найти в статье о пространствах основных функций и распределений .

Полные нормы против полных топологических векторных пространств

Помимо метрической полноты, существует еще одно понятие полноты — понятие полного топологического векторного пространства (TVS) или TVS-полноты, которое использует теорию равномерных пространств . В частности, понятие TVS-полноты использует уникальную трансляционно-инвариантную однородность , называемую канонической однородностью , которая зависит только от векторного вычитания и топологии. $\tau$ что векторное пространство наделено, и поэтому, в частности, это понятие TVS-полноты не зависит от какой-либо нормы, индуцирующей топологию $\tau$(и даже относится к ТВС, даже не метризуемым). Каждое банахово пространство является полным TVS. Более того, нормированное пространство является банаховым (то есть его индуцированная нормой метрика полна) тогда и только тогда, когда оно полно как топологическое векторное пространство. Если $(X,\tau )$ является метризуемым топологическим векторным пространством (например, любой топологией, индуцированной нормой), тогда $(X,\tau )$ является полной TVS тогда и только тогда, когда она является секвенциально полной TVS, а это означает, что достаточно проверить, что каждая последовательность Коши в $(X,\tau )$ сходится в $(X,\tau )$ в какой-то момент $X$ (т. е. нет необходимости рассматривать более общее понятие произвольных сетей Коши ).

Если $(X,\tau )$ — топологическое векторное пространство, топология которого индуцирована некоторой (возможно, неизвестной) нормой (такие пространства называются нормируемыми ), тогда $(X,\tau )$ является полным топологическим векторным пространством тогда и только тогда, когда $X$ может быть присвоена норма $\|\cdot \|$ что вызывает $X$ топология $\tau$ а также делает $(X,\|\cdot \|)$в банахово пространство. Хаусдорфово . локально выпуклое топологическое векторное пространство $X$ нормировано сильное тогда и только тогда, когда его двойственное пространство $X_{b}^{\prime }$ является нормальным, в таком случае $X_{b}^{\prime }$ является банаховым пространством ( $X_{b}^{\prime }$ обозначает сильное дуальное пространство $X,$ топология которого является обобщением двойственной топологии, индуцированной нормой, на непрерывном дуальном пространстве $X^{\prime }$; см. эту сноску Больше подробностей). Если $X$ — метризуемая локально выпуклая TVS, то $X$ является нормальным тогда и только тогда, когда $X_{b}^{\prime }$ является пространством Фреше–Урысона . Это показывает, что в категории локально выпуклых ТВС банаховыми пространствами являются в точности те полные пространства, которые одновременно метризуемы и имеют метризуемые сильные дуальные пространства .

Завершения

Каждое нормированное пространство можно изометрически вложить в плотное векторное подпространство некоторого банахова пространства, где это банахово пространство называется пополнением нормированного пространства. Это хаусдорфово пополнение единственно с точностью до изометрического изоморфизма.

Точнее, для каждого нормированного пространства $X,$ существует банахово пространство $Y$ и отображение $T:X\to Y$ такой, что $T$ является изометрическим отображением и $T(X)$ плотный в $Y.$ Если $Z$ — другое банахово пространство такое, что существует изометрический изоморфизм из $X$ на плотное подмножество $Z,$ затем $Z$ изометрически изоморфен $Y.$ Это банахово пространство $Y$ является хаусдорфовым пополнением нормированного пространства $X.$ Базовое метрическое пространство для $Y$ то же самое, что и метрическое завершение $X,$ с операциями в векторном пространстве, расширенными из $X$ к $Y.$ Завершение $X$ иногда обозначается ${\widehat {X}}.$

Общая теория

Линейные операторы, изоморфизмы

Основная статья: Ограниченный оператор

Если $X$ и $Y$ являются нормированными пространствами над одним и тем же основным полем $\mathbb {K} ,$ совокупность всех непрерывных $\mathbb {K}$-линейные карты $T:X\to Y$ обозначается $B(X,Y).$В бесконечномерных пространствах не все линейные карты непрерывны. Линейное отображение нормированного пространства $X$ в другое нормированное пространство, непрерывно тогда и только тогда, когда оно ограничено на замкнутом единичном шаре $X.$ Таким образом, векторное пространство $B(X,Y)$ можно задать операторную норму

$$\|T\|=\sup \left\{\|Tx\|_{Y}\mid x\in X,\ \|x\|_{X}\leq 1\right\}.$$

Для $Y$ банахово пространство, пространство $B(X,Y)$является банаховым пространством относительно этой нормы. В категориальном контексте иногда удобно ограничить функциональное пространство между двумя банаховыми пространствами только короткими отображениями ; в этом случае пространство $B(X,Y)$ вновь появляется как естественный бифунктор .

Если $X$ является банаховым пространством, пространство $B(X)=B(X,X)$образует банахову алгебру с единицей ; операция умножения задается композицией линейных отображений.

Если $X$ и $Y$ являются нормированными пространствами, они являются изоморфными нормированными пространствами , если существует линейная биекция $T:X\to Y$ такой, что $T$ и его инверсия $T^{-1}$являются непрерывными. Если одно из двух пространств $X$ или $Y$является полным (или рефлексивным , сепарабельным и т. д.), то таким же является и другое пространство. Два нормированных пространства $X$ и $Y$ , изометрически изоморфны если, кроме того, $T$ является изометрией , то есть $\|T(x)\|=\|x\|$ для каждого $x$ в $X.$ Расстояние Банаха –Мазура $d(X,Y)$ между двумя изоморфными, но не изометрическими пространствами $X$ и $Y$ дает меру того, сколько двух пространств $X$ и $Y$ различаются.

Непрерывные и ограниченные линейные

Каждый непрерывный линейный оператор является ограниченным линейным оператором , и если мы имеем дело только с нормированными пространствами, то обратное также верно. То есть линейный оператор между двумя нормированными пространствами ограничен тогда и только тогда, когда он является непрерывной функцией . В частности, потому что скалярное поле (которое $\mathbb {R}$ или $\mathbb {C}$) — нормированное пространство, линейный функционал на нормированном пространстве является ограниченным линейным функционалом тогда и только тогда, когда он является непрерывным линейным функционалом . Это позволяет применять результаты, связанные с непрерывностью (подобные приведенным ниже), к банаховым пространствам. Хотя ограниченность — это то же самое, что непрерывность для линейных отображений между нормированными пространствами, термин «ограниченный» чаще используется, когда речь идет в первую очередь о банаховых пространствах.

Если $f:X\to \mathbb {R}$ является субаддитивной функцией (такой как норма, сублинейная функция или действительный линейный функционал), тогда $f$ непрерывно в начале координат тогда и только тогда, когда $f$ на равномерно непрерывен всех $X$; и если вдобавок $f(0)=0$ затем $f$ является непрерывным тогда и только тогда, когда его абсолютное значение $|f|:X\to [0,\infty )$ непрерывно, что происходит тогда и только тогда, когда $\{x\in X:|f(x)|<1\}$ является открытым подмножеством $X.$ И что очень важно для применения теоремы Хана–Банаха , линейный функционал $f$ непрерывен тогда и только тогда, когда это верно в отношении его действительной части $\operatorname {Re} f$ и более того, $\|\operatorname {Re} f\|=\|f\|$ и реальная часть $\operatorname {Re} f$ полностью определяет $f,$поэтому теорему Хана–Банаха часто формулируют только для вещественных линейных функционалов. Кроме того, линейный функционал $f$ на $X$ непрерывна тогда и только тогда, когда полунорма $|f|$ является непрерывным, что происходит тогда и только тогда, когда существует непрерывная полунорма $p:X\to \mathbb {R}$ такой, что $|f|\leq p$; это последнее утверждение, включающее линейный функционал $f$ и полунорма $p$ встречается во многих версиях теоремы Хана–Банаха.

Основные понятия

Декартово произведение $X\times Y$двух нормированных пространств канонически не снабжено нормой. Однако обычно используются несколько эквивалентных норм: такой как

$$\|(x,y)\|_{1}=\|x\|+\|y\|,\qquad \|(x,y)\|_{\infty }=\max(\|x\|,\|y\|)$$

которые соответствуют (соответственно) копроизведению и произведению в категории банаховых пространств и коротких отображений (обсужденных выше). Для конечных (ко)произведений эти нормы порождают изоморфные нормированные пространства, а произведение $X\times Y$ (или прямая сумма $X\oplus Y$) является полным тогда и только тогда, когда оба фактора полны.

Если $M$ — замкнутое линейное подпространство нормированного пространства $X,$ существует естественная норма в факторпространстве $X/M,$

$$\|x+M\|=\inf \limits _{m\in M}\|x+m\|.$$

Частное $X/M$ является банаховым пространством, когда $X$ завершено. Карта отношений из $X$ на $X/M,$ отправка $x\in X$ своему классу $x+M,$ линейна, на и имеет норму $1,$ кроме случаев, когда $M=X,$ в этом случае частное представляет собой нулевое пространство.

Замкнутое линейное подпространство $M$ из $X$ называется дополненным подпространством $X$ если $M$ - это образ сюръективной ограниченной линейной проекции $P:X\to M.$ В этом случае пространство $X$ изоморфна прямой сумме $M$ и $\ker P,$ ядро проекции $P.$

Предположим, что $X$ и $Y$ являются банаховыми пространствами и что $T\in B(X,Y).$ Существует факторизация каноническая $T$ как

$$T=T_{1}\circ \pi ,\ \ \ T:X\ {\overset {\pi }{\longrightarrow }}\ X/\ker(T)\ {\overset {T_{1}}{\longrightarrow }}\ Y$$

где первая карта $\pi$ является фактор-картой, а вторая карта $T_{1}$ отправляет каждый класс $x+\ker T$ в частном к изображению $T(x)$ в $Y.$Это четко определено, поскольку все элементы одного класса имеют одно и то же изображение. Отображение $T_{1}$ является линейной биекцией из $X/\ker T$ на диапазон $T(X),$ обратное для которого не обязательно должно быть ограничено.

Классические пространства

Основные примеры банаховых пространств включают: пространства Lp $L^{p}$ и их частные случаи, пространства последовательностей $\ell ^{p}$ состоящие из скалярных последовательностей, индексированных натуральными числами $\mathbb {N}$; среди них пространство $\ell ^{1}$ абсолютно суммируемых последовательностей и пространства $\ell ^{2}$суммируемых с квадратом последовательностей; космос $c_{0}$ последовательностей, стремящихся к нулю, и пространства $\ell ^{\infty }$ограниченных последовательностей; космос $C(K)$ непрерывных скалярных функций на компактном хаусдорфовом пространстве $K,$ оснащен максимальной нормой,

$$\|f\|_{C(K)}=\max\{|f(x)|:x\in K\},\quad f\in C(K).$$

Согласно теореме Банаха–Мазура , каждое банахово пространство изометрически изоморфно подпространству некоторого $C(K).$ Для каждого сепарабельного банахова пространства $X,$ есть закрытое подпространство $M$ из $\ell ^{1}$ такой, что $X:=\ell ^{1}/M.$

Любое гильбертово пространство служит примером банахового пространства. Гильбертово пространство $H$ на $\mathbb {K} =\mathbb {R} ,\mathbb {C}$ полно для нормы вида

$$\|x\|_{H}={\sqrt {\langle x,x\rangle }},$$

где

$$\langle \cdot ,\cdot \rangle :H\times H\to \mathbb {K}$$

— внутренний продукт , линейный по первому аргументу и удовлетворяющий следующему:

$${\begin{aligned}\langle y,x\rangle &={\overline {\langle x,y\rangle }},\quad {\text{ for all }}x,y\in H\\\langle x,x\rangle &\geq 0,\quad {\text{ for all }}x\in H\\\langle x,x\rangle =0{\text{ if and only if }}x&=0.\end{aligned}}$$

Например, пространство $L^{2}$ является гильбертовым пространством.

Пространства Харди , пространства Соболева являются примерами банаховых пространств, связанных с $L^{p}$пространства и имеют дополнительную структуру. Они важны в различных областях анализа, в том числе в гармоническом анализе и уравнениях в частных производных .

Банаховые алгебры

Банахова алгебра — это банахово пространство. $A$ над $\mathbb {K} =\mathbb {R}$ или $\mathbb {C} ,$ вместе со структурой алгебры над $\mathbb {K}$, такой, что карта продукта $A\times A\ni (a,b)\mapsto ab\in A$является непрерывным. Эквивалентная норма по $A$ можно найти так, что $\|ab\|\leq \|a\|\|b\|$ для всех $a,b\in A.$

Примеры

• Банахово пространство $C(K)$ с поточечным произведением является банаховой алгеброй.
• Дисковая алгебра $A(\mathbf {D} )$ состоит из функций, голоморфных в открытом единичном круге $D\subseteq \mathbb {C}$ и непрерывен при его закрытии : ${\overline {\mathbf {D} }}.$ Оснащен максимальной нормой на ${\overline {\mathbf {D} }},$ дисковая алгебра $A(\mathbf {D} )$ является замкнутой подалгеброй $C\left({\overline {\mathbf {D} }}\right).$
• Алгебра Винера $A(\mathbf {T} )$ — алгебра функций на единичной окружности $\mathbf {T}$с абсолютно сходящимся рядом Фурье. Через карту, связывающую функцию с $\mathbf {T}$ последовательности своих коэффициентов Фурье эта алгебра изоморфна банаховой алгебре $\ell ^{1}(Z),$ где произведение представляет собой свертку последовательностей.
• Для каждого банахова пространства $X,$ космос $B(X)$ ограниченных линейных операторов на $X,$ с композицией карт в качестве произведения, является банаховой алгеброй.
• C *-алгебра — это комплексная банахова алгебра. $A$ с антилинейной инволюцией $a\mapsto a^{*}$ такой, что $\left\|a^{*}a\right\|=\|a\|^{2}.$ Космос $B(H)$ ограниченных линейных операторов в гильбертовом пространстве $H$является фундаментальным примером C*-алгебры. Теорема Гельфанда –Наймарка утверждает, что каждая C*-алгебра изометрически изоморфна C*-подалгебре некоторой $B(H).$ Космос $C(K)$ комплексных непрерывных функций на компактном хаусдорфовом пространстве $K$ является примером коммутативной C*-алгебры, где инволюция соответствует каждой функции $f$ его комплексное сопряжение ${\overline {f}}.$

Двойной пробел

Основная статья: Двойное пространство

Если $X$ является нормированным пространством и $\mathbb {K}$ базовое поле (действительное или комплексное число ), непрерывное двойственное пространство — это пространство непрерывных линейных отображений из $X$ в $\mathbb {K} ,$или непрерывные линейные функционалы . Обозначение непрерывного двойственного $X^{\prime }=B(X,\mathbb {K} )$ в этой статье. С $\mathbb {K}$ является банаховым пространством (с использованием абсолютного значения в качестве нормы), двойственное $X^{\prime }$ является банаховым пространством для любого нормированного пространства $X.$ Теорема Диксмье –Нга характеризует пространства, двойственные банаховым пространствам.

Основным инструментом доказательства существования непрерывных линейных функционалов является теорема Хана–Банаха .

Теорема Хана – Банаха . Пусть $X$ быть векторным пространством над полем $\mathbb {K} =\mathbb {R} ,\mathbb {C} .$ Пусть дальше

• $Y\subseteq X$ быть линейным подпространством ,
• $p:X\to \mathbb {R}$ быть сублинейной функцией и
• $f:Y\to \mathbb {K}$ быть линейным функционалом , так что $\operatorname {Re} (f(y))\leq p(y)$ для всех $y\in Y.$

Тогда существует линейный функционал $F:X\to \mathbb {K}$ так что

$$F{\big \vert }_{Y}=f,\quad {\text{ and }}\quad {\text{ for all }}x\in X,\ \ \operatorname {Re} (F(x))\leq p(x).$$

В частности, всякий непрерывный линейный функционал на подпространстве нормированного пространства можно непрерывно продолжить на все пространство, не увеличивая норму функционала. Важным частным случаем является следующий: для каждого вектора $x$ в нормированном пространстве $X,$ существует непрерывный линейный функционал $f$ на $X$ такой, что

$$f(x)=\|x\|_{X},\quad \|f\|_{X^{\prime }}\leq 1.$$

Когда $x$ не равен $\mathbf {0}$ вектор, функционал $f$ должен иметь норму один и называется нормирующим функционалом для $x.$

Теорема Хана-Банаха о разделении утверждает, что два непересекающихся непустых выпуклых множества в реальном банаховом пространстве, одно из которых открытое, могут быть разделены замкнутой аффинной гиперплоскостью . Открытое выпуклое множество лежит строго по одну сторону от гиперплоскости, второе выпуклое множество лежит по другую сторону, но может касаться гиперплоскости.

Подмножество $S$ в банаховом пространстве $X$ является полным , если линейный интервал $S$ плотный ​ в $X.$ Подмножество $S$ Всего в $X$ тогда и только тогда, когда единственный непрерывный линейный функционал, обращающийся в нуль на $S$ это $\mathbf {0}$ функционал: эта эквивалентность следует из теоремы Хана – Банаха.

Если $X$ является прямой суммой двух замкнутых линейных подпространств $M$ и $N,$ тогда двойной $X^{\prime }$ из $X$ изоморфна прямой сумме двойственных чисел $M$ и $N.$ Если $M$ является замкнутым линейным подпространством в $X,$ можно связать ортогональ $M$ в двойном,

$$M^{bot}=\left\{x^{\prime }\in X:x^{\prime }(m)=0,\ {\text{ for all }}m\in M\right\}.$$

Ортогональный $M^{\bot }$является замкнутым линейным подпространством двойственного. Двойник $M$ изометрически изоморфен $X'/M^{\bot }.$ Двойник $X/M$ изометрически изоморфен $M^{\bot }.$

Двойственное сепарабельному банаховому пространству не обязательно должно быть сепарабельным, но:

Теорема - Позволять $X$быть нормированным пространством. Если $X'$ отделим , то $X$ является разделимым.

Когда $X'$ сепарабельно, то приведенный выше критерий полноты можно использовать для доказательства существования счетного тотального подмножества в $X.$

Слабые топологии

Слабая топология в банаховом пространстве. $X$ это самая грубая топология на $X$ для которого все элементы $x^{\prime }$ в непрерывном двойственном пространстве $X^{\prime }$являются непрерывными. Таким образом, нормальная топология тоньше слабой топологии. Из теоремы Хана–Банаха о разделении следует, что слабая топология является Хаусдорфовой и что выпуклое по норме подмножество банахова пространства также слабо замкнуто. Непрерывное по норме линейное отображение между двумя банаховыми пространствами $X$ и $Y$ также слабо непрерывен , т. е. непрерывен из слабой топологии $X$ к тому из $Y.$

Если $X$бесконечномерен, существуют линейные отображения, которые не являются непрерывными. Космос $X^{*}$ всех линейных карт из $X$ к основному полю $\mathbb {K}$ (это пространство $X^{*}$ называется алгебраическим дуальным пространством , чтобы отличить его от $X^{\prime }$ также индуцирует топологию на $X$ которая тоньше слабой топологии и гораздо реже используется в функциональном анализе.

В двойном пространстве $X^{\prime },$ существует топология более слабая, чем слабая топология $X^{\prime },$называется слабой* топологией . Это самая грубая топология на $X^{\prime }$ для которого все оценочные карты $x^{\prime }\in X^{\prime }\mapsto x^{\prime }(x),$ где $x$ колеблется в пределах $X,$являются непрерывными. Его важность вытекает из теоремы Банаха – Алаоглу .

Теорема Банаха – Алаоглу . Пусть $X$быть нормированным векторным пространством . Тогда замкнутый единичный шар $B=\left\{x\in X:\|x\|\leq 1\right\}$ дуального пространства компактно в слабой* топологии.

Теорему Банаха–Алаоглу можно доказать, используя теорему Тихонова о бесконечных произведениях компактов Хаусдорфа. Когда $X$ отделим, единичный шар $B^{\prime }$ двойственного является метризуемым компактом в слабой* топологии.

Примеры двойных пробелов

Двойник $c_{0}$ изометрически изоморфен $\ell ^{1}$: для любого ограниченного линейного функционала $f$ на $c_{0},$ есть уникальный элемент $y=\left\{y_{n}\right\}\in \ell ^{1}$ такой, что

$$f(x)=\sum _{n\in \mathbb {N} }x_{n}y_{n},\qquad x=\{x_{n}\}\in c_{0},\ \ {\text{and}}\ \ \|f\|_{(c_{0})'}=\|y\|_{\ell _{1}}.$$

Двойник $\ell ^{1}$ изометрически изоморфен $\ell ^{\infty }$. Двойственное пространству Лебега $L^{p}([0,1])$ изометрически изоморфен $L^{q}([0,1])$ когда $1\leq p<\infty$ и ${\frac {1}{p}}+{\frac {1}{q}}=1.$

Для каждого вектора $y$ в гильбертовом пространстве $H,$ картографирование

$$x\in H\to f_{y}(x)=\langle x,y\rangle$$

определяет непрерывный линейный функционал $f_{y}$ на $H.$Теорема о представлении Рисса утверждает, что каждый непрерывный линейный функционал на $H$ имеет форму $f_{y}$ для однозначно определенного вектора $y$ в $H.$ Отображение $y\in H\to f_{y}$ представляет собой антилинейную изометрическую биекцию из $H$ на свой двойной $H'.$ Когда скаляры действительны, это отображение является изометрическим изоморфизмом.

Когда $K$ — компактное топологическое пространство Хаусдорфа, двойственное $M(K)$ из $C(K)$ — пространство мер Радона по Бурбаки. Подмножество $P(K)$ из $M(K)$ состоящее из неотрицательных мер массы 1 ( вероятностных мер ), является выпуклым w*-замкнутым подмножеством единичного шара $M(K).$ Крайние точки г. $P(K)$ являются ли Дирака меры $K.$ Набор мер Дирака на $K,$ снабженный w*-топологией гомеоморфен , $K.$

Теорема Банаха – Стоуна — если $K$ и $L$ являются компактными хаусдорфовыми пространствами и если $C(K)$ и $C(L)$ изометрически изоморфны, то топологические пространства $K$ и $L$ гомеоморфны ​ .

Результат был расширен Амиром и Камберн к случаю, когда мультипликативное расстояние Банаха–Мазура между $C(K)$ и $C(L)$ является $<2.$ Теорема перестает быть верной, если расстояние равно $=2.$

В коммутативной банаховой алгебре $C(K),$ максимальные идеалы являются в точности ядрами мер Дирака на $K,$

$$I_{x}=\ker \delta _{x}=\{f\in C(K):f(x)=0\},\quad x\in K.$$

В более общем смысле, по теореме Гельфанда–Мазура , максимальные идеалы коммутативной банаховой алгебры с единицей могут быть отождествлены с ее характерами — не просто как множества, но и как топологические пространства: первые с топологией оболочки-ядра , а вторые с топологией w*. -топология. В этой идентификации максимальное идеальное пространство можно рассматривать как aw*-компактное подмножество единичного шара в двойственном $A'.$

Теорема — Если $K$ — компактное хаусдорфово пространство, то максимальное идеальное пространство $\Xi$ банаховой алгебры $C(K)$ гомеоморфен ​ ​ $K.$

Не каждая коммутативная банахова алгебра с единицей имеет вид $C(K)$ для некоторого компактного хаусдорфова пространства $K.$ Однако это утверждение справедливо, если положить $C(K)$в меньшей категории коммутативных C*-алгебр . Гельфанда Теорема о представлении коммутативных C*-алгебр утверждает, что каждая коммутативная единичная C *-алгебра $A$ изометрически изоморфен $C(K)$ космос. Компакт Хаусдорфа. $K$ здесь снова максимальное идеальное пространство, называемое спектром также $A$ в контексте C*-алгебры.

Бидуальный

См. также: Бидуальное , Рефлексивное пространство и Полурефлексивное пространство.

Если $X$ является нормированным пространством, (непрерывным) двойственным $X''$ двойного $X'$ называется двусторонний , или второй двойной $X.$ Для каждого нормированного пространства $X,$ есть естественная карта,

$${\begin{cases}F_{X}:X\to X''\\F_{X}(x)(f)=f(x)&{\text{ for all }}x\in X,{\text{ and for all }}f\in X'\end{cases}}$$

Это определяет $F_{X}(x)$ как непрерывный линейный функционал на $X^{\prime },$ то есть элемент $X^{\prime \prime }.$ Карта $F_{X}:x\to F_{X}(x)$ представляет собой линейную карту из $X$ к $X^{\prime \prime }.$ Вследствие существования нормирующего функционала $f$ для каждого $x\in X,$ эта карта $F_{X}$ изометричен, следовательно, инъективен .

Например, двойник $X=c_{0}$ отождествляется с $\ell ^{1},$ и двойник $\ell ^{1}$ отождествляется с $\ell ^{\infty },$пространство ограниченных скалярных последовательностей. Под этими отождествлениями $F_{X}$ это карта включения из $c_{0}$ к $\ell ^{\infty }.$ Это действительно изометрия, но не на.

Если $F_{X}$ сюръективно , то нормированное пространство $X$называется рефлексивным (см. ниже ). Будучи двойственным нормированному пространству, бидуальное $X''$ полно, следовательно, всякое рефлексивное нормированное пространство является банаховым пространством.

Использование изометрического встраивания $F_{X},$ принято считать нормированным пространством $X$как подмножество своего бидуала. Когда $X$ является банаховым пространством, оно рассматривается как замкнутое линейное подпространство $X^{\prime \prime }.$ Если $X$ не рефлексивно, единичный шар $X$ является собственным подмножеством единичного шара $X^{\prime \prime }.$ утверждает Теорема Голдстайна , что единичный шар нормированного пространства слабо*-плотен в единичном шаре бидуального пространства. Другими словами, для каждого $x''$ в бидуале существует сеть $\left(x_{i}\right)_{i\in I}$ в $X$ так что

$$\sup _{i\in I}\left\|x_{i}\right\|\leq \|x''\|,\ \ x''(f)=\lim _{i}f\left(x_{i}\right),\quad f\in X'.$$

Сеть может быть заменена слабо*-сходящейся последовательностью, когда двойственная $X'$является разделимым. С другой стороны, элементы бидуального $\ell ^{1}$ которых нет в $\ell ^{1}$ не может быть слабым*-пределом последовательностей в $\ell ^{1},$ с $\ell ^{1}$ является слабо секвенциально полным .

Теоремы Банаха

Вот основные общие результаты о банаховых пространствах, восходящие ко временам книги Банаха ( Банах (1932) ) и связанные с теоремой Бэра о категориях . Согласно этой теореме, полное метрическое пространство (такое как банахово пространство, пространство Фреше или F-пространство ) не может быть равно объединению счетного числа замкнутых подмножеств с пустыми внутренностями . Следовательно, банахово пространство не может быть объединением счетного числа замкнутых подпространств, если оно уже не равно одному из них; Банахово пространство со счетным базисом Гамеля конечномерно.

Теорема Банаха – Штейнхауза . Пусть $X$ быть банаховым пространством и $Y$быть нормированным векторным пространством . Предположим, что $F$ представляет собой набор непрерывных линейных операторов из $X$ к $Y.$ Принцип равномерной ограниченности гласит, что если для всех $x$ в $X$ у нас есть $\sup _{T\in F}\|T(x)\|_{Y}<\infty ,$ затем $\sup _{T\in F}\|T\|_{Y}<\infty .$

Теорема Банаха–Штайнхауза не ограничивается банаховыми пространствами. Его можно распространить, например, на случай, когда $X$ является пространством Фреше при условии, что заключение будет изменено следующим образом: при той же гипотезе существует окрестность $U$ из $\mathbf {0}$ в $X$ такой, что все $T$ в $F$ равномерно ограничены $U,$

$$\sup _{T\in F}\sup _{x\in U}\;\|T(x)\|_{Y}<\infty .$$

Теорема открытого отображения . Пусть $X$ и $Y$ быть банаховыми пространствами и $T:X\to Y$ — сюръективный непрерывный линейный оператор, то $T$ это открытая карта.

Следствие . Каждый взаимно однозначный ограниченный линейный оператор из банахова пространства в банахово пространство является изоморфизмом.

Первая теорема об изоморфизме банаховых пространств . Предположим, что $X$ и $Y$ являются банаховыми пространствами и что $T\in B(X,Y).$ Предположим далее, что диапазон $T$ закрыт в $Y.$ Затем $X/\ker T$ изоморфен $T(X).$

Этот результат является прямым следствием предыдущей банаховой теоремы об изоморфизме и канонической факторизации ограниченных линейных отображений.

Следствие . Если банахово пространство $X$ — внутренняя прямая сумма замкнутых подпространств $M_{1},\ldots ,M_{n},$ затем $X$ изоморфен $M_{1}\oplus \cdots \oplus M_{n}.$

Это еще одно следствие теоремы об изоморфизме Банаха, примененной к непрерывной биекции из $M_{1}\oplus \cdots \oplus M_{n}$ на $X$ отправка $m_{1},\cdots ,m_{n}$ к сумме $m_{1}+\cdots +m_{n}.$

Теорема о замкнутом графе . Пусть $T:X\to Y$— линейное отображение банаховых пространств. График $T$ закрыт в $X\times Y$ если и только если $T$ является непрерывным.

Рефлексивность

Основная статья: Рефлексивное пространство

Нормированное пространство $X$ называется рефлексивным , если естественное отображение

$${\begin{cases}F_{X}:X\to X''\\F_{X}(x)(f)=f(x)&{\text{ for all }}x\in X,{\text{ and for all }}f\in X'\end{cases}}$$

является сюръективным. Рефлексивные нормированные пространства являются банаховыми пространствами.

Теорема — Если $X$ — рефлексивное банахово пространство, каждое замкнутое подпространство которого $X$ и каждое факторпространство $X$ являются рефлексивными.

Это следствие теоремы Хана–Банаха. Далее, по теореме об открытом отображении, если существует ограниченный линейный оператор из банахова пространства $X$ в банахово пространство $Y,$ затем $Y$ является рефлексивным.

Теорема — Если $X$ является банаховым пространством, то $X$ рефлексивно тогда и только тогда, когда $X^{\prime }$ является рефлексивным.

Следствие — Пусть $X$— рефлексивное банахово пространство. Затем $X$ отделим когда тогда и только тогда, $X^{\prime }$ является разделимым.

Действительно, если двойственный $Y^{\prime }$ банахова пространства $Y$ сепарабельна, то $Y$является разделимым. Если $X$ рефлексивно и сепарабельно, то двойственное $X^{\prime }$ является отделимым, поэтому $X^{\prime }$ является разделимым.

Теорема . Предположим, что $X_{1},\ldots ,X_{n}$ являются нормированными пространствами и что $X=X_{1}\oplus \cdots \oplus X_{n}.$ Затем $X$ рефлексивно тогда и только тогда, когда каждое $X_{j}$ является рефлексивным.

Гильбертовые пространства рефлексивны. $L^{p}$ пространства рефлексивны, когда $1<p<\infty .$В более общем смысле, , равномерно выпуклые пространства рефлексивны согласно теореме Милмана-Петтиса . Пространства $c_{0},\ell ^{1},L^{1}([0,1]),C([0,1])$не являются рефлексивными. В этих примерах нерефлексивных пространств $X,$ двусторонний $X''$ «намного больше», чем $X.$ А именно, при естественном изометрическом вложении $X$ в $X''$ заданный теоремой Хана–Банаха, фактор $X^{\prime \prime }/X$бесконечномерен и даже неразделим. Однако Роберт К. Джеймс построил пример нерефлексивного пространства, обычно называемого « пространством Джеймса » и обозначаемого $J,$ такой, что частное $J^{\prime \prime }/J$является одномерным. Более того, это пространство $J$ изометрически изоморфен своему бидуалу.

Теорема . Банахово пространство . $X$ рефлексивно тогда и только тогда, когда его единичный шар компактен в слабой топологии .

Когда $X$ рефлексивно, то из этого следует, что все замкнутые и ограниченные выпуклые подмножества $X$слабо компактны. В гильбертовом пространстве $H,$ слабая компактность единичного шара очень часто используется следующим образом: каждая ограниченная последовательность в $H$ имеет слабо сходящиеся подпоследовательности.

Слабая компактность единичного шара дает инструмент для поиска решений в рефлексивных пространствах некоторых оптимизационных задач . Например, каждая выпуклая непрерывная функция на единичном шаре $B$ рефлексивного пространства достигает своего минимума в некоторой точке $B.$

Как частный случай предыдущего результата, когда $X$ представляет собой рефлексивное пространство над $\mathbb {R} ,$ каждый непрерывный линейный функционал $f$ в $X^{\prime }$ достигает своего максимума $\|f\|$ на единичном шаре $X.$ Следующая теорема Роберта Джеймса дает обратное утверждение.

Теорема Джеймса . Для банахового пространства следующие два свойства эквивалентны:

• $X$ является рефлексивным.
• для всех $f$ в $X^{\prime }$ Существует $x\in X$ с $\|x\|\leq 1,$ так что $f(x)=\|f\|.$

Теорему можно расширить, чтобы дать характеристику слабо компактных выпуклых множеств.

О каждом нерефлексивном банаховом пространстве $X,$существуют непрерывные линейные функционалы, не доходящие до нормы . Однако Бишопа – Фелпса теорема утверждает, что функционалы, достигающие нормы, плотны по норме в двойственном $X^{\prime }$ из $X.$

Слабые сходимости последовательностей

Последовательность $\left\{x_{n}\right\}$ в банаховом пространстве $X$ к слабо сходится вектору $x\in X$ если $\left\{f\left(x_{n}\right)\right\}$ сходится к $f(x)$ для любого непрерывного линейного функционала $f$ в двойном $X^{\prime }.$ Последовательность $\left\{x_{n}\right\}$ является слабо Коши-последовательностью , если $\left\{f\left(x_{n}\right)\right\}$ сходится к скалярному пределу $L(f),,$ для каждого $f$ в $X^{\prime }.$ Последовательность $\left\{f_{n}\right\}$ в двойном $X^{\prime }$ слабо * сходится к функционалу $f\in X^{\prime }$ если $f_{n}(x)$ сходится к $f(x)$ для каждого $x$ в $X.$ Слабо* сходящиеся последовательности, слабо сходящиеся и слабо сходящиеся последовательности Коши ограничены по норме, как следствие теоремы Банаха–Штайнхауза .

Когда последовательность $\left\{x_{n}\right\}$ в $X$ является слабо Коши, предел $L$ выше определяет ограниченный линейный функционал на двойственном $X^{\prime },$ то есть элемент $L$ бидуального $X,$ и $L$ это предел $\left\{x_{n}\right\}$в слабой*-топологии бидуала. Банахово пространство $X$ является слабо секвенциально полной, если каждая слабо секвенциально полная последовательность слабо сходится в $X.$ Из предыдущего обсуждения следует, что рефлексивные пространства слабо секвенциально полны.

Теорема — Для каждой меры $\mu ,$ космос $L^{1}(\mu )$ является слабо секвенциально полным.

Ортонормированная последовательность в гильбертовом пространстве является простым примером слабо сходящейся последовательности с пределом, равным $\mathbf {0}$вектор. единичного вектора Базис $\ell ^{p}$ для $1<p<\infty ,$ или из $c_{0},$ является еще одним примером слабо нулевой последовательности , то есть последовательности, которая слабо сходится к $\mathbf {0} .$ Для каждой слабонулевой последовательности в банаховом пространстве существует последовательность выпуклых комбинаций векторов из данной последовательности, сходящаяся по норме к $\mathbf {0} .$

Базис единичного вектора $\ell ^{1}$не является слабо Коши. Слабые последовательности Коши в $\ell ^{1}$ слабо сходятся, так как $L^{1}$-пространства слабо секвенциально полны. Действительно, слабо сходящиеся последовательности в $\ell ^{1}$ сходятся по норме. Это значит, что $\ell ^{1}$ удовлетворяет свойству Шура .

Результаты, включающие $\ell ^{1}$ основа

Слабые последовательности Коши и $\ell ^{1}$ В основе лежат противоположные случаи дихотомии, установленные в следующем глубоком результате Г. П. Розенталя.

Теорема - Позволять $\left\{x_{n}\right\}_{n\in \mathbb {N} }$— ограниченная последовательность в банаховом пространстве. Или $\left\{x_{n}\right\}_{n\in \mathbb {N} }$ имеет слабо подпоследовательность Коши или допускает подпоследовательность, эквивалентную стандартному базису единичных векторов $\ell ^{1}.$

Дополнение к этому результату принадлежит Оделлу и Розенталю (1975).

Теорема - Позволять $X$— сепарабельное банахово пространство. Следующие действия эквивалентны:

• Космос $X$ не содержит замкнутого подпространства, изоморфного $\ell ^{1}.$
• Каждый элемент бидуала $X''$ является слабым*-пределом последовательности $\left\{x_{n}\right\}$ в $X.$

По теореме Голдстайна каждый элемент единичного шара $B^{\prime \prime }$ из $X^{\prime \prime }$ является слабым*-пределом сети в единичном шаре $X.$ Когда $X$ не содержит $\ell ^{1},$ каждый элемент $B^{\prime \prime }$ является слабым*-пределом последовательности в единичном шаре $X.$

Когда банахово пространство $X$ сепарабельна, единичный шар двойственной $X^{\prime },$ наделенный слабой*-топологией, является метризуемым компактом $K,$ и каждый элемент $x^{\prime \prime }$ в бидуальном $X^{\prime \prime }$ определяет ограниченную функцию на $K$:

$$x'\in K\mapsto x''(x'),\quad \left|x''(x')\right|\leq \left\|x''\right\|.$$

Эта функция непрерывна для компактной топологии $K$ если и только если $x^{\prime \prime }$ на самом деле находится в $X,$ рассматривается как подмножество $X^{\prime \prime }.$ Кроме того, в остальной части параграфа предположим, что $X$ не содержит $\ell ^{1}.$ По предыдущему результату Оделла и Розенталя функция $x^{\prime \prime }$ является пределом поточечным $K$ последовательности $\left\{x_{n}\right\}\subseteq X$ непрерывных функций на $K,$ следовательно, это функция первого класса Бэра на $K.$ Единичный шар бидуала — это поточечно-компактное подмножество первого класса Бэра на $K.$

Последовательности, слабая и слабая* компактность

Когда $X$ сепарабельен, единичный шар двойственного элемента слабо*-компактен по теореме Банаха–Алаоглу и метризуем для слабой* топологии, следовательно, каждая ограниченная последовательность в двойственной последовательности имеет слабо* сходящиеся подпоследовательности. Это относится к сепарабельным рефлексивным пространствам, но в данном случае верно и другое, как указано ниже.

Слабая топология банахова пространства. $X$ метризуемо тогда и только тогда, когда $X$ является конечномерным. Если двойной $X'$ сепарабельна, слабая топология единичного шара $X$метризуема. Это относится, в частности, к сепарабельным рефлексивным банаховым пространствам. Хотя слабая топология единичного шара, вообще говоря, не метризуема, слабую компактность можно охарактеризовать с помощью последовательностей.

Теорема Эберлейна – Шмуляна - Множество $A$ в банаховом пространстве относительно слабо компактна тогда и только тогда, когда каждая последовательность $\left\{a_{n}\right\}$ в $A$ имеет слабо сходящуюся подпоследовательность.

Банахово пространство $X$ рефлексивна тогда и только тогда, когда каждая ограниченная последовательность из $X$ имеет слабо сходящуюся подпоследовательность.

Слабо компактное подмножество $A$ в $\ell ^{1}$является норм-компактным. Действительно, каждая последовательность в $A$ имеет слабо сходящиеся подпоследовательности по Эберлейну–Шмулиану, которые сходятся по норме в силу свойства Шура $\ell ^{1}.$

Тип и котип

Основная статья: Тип и котип банахового пространства

Способ классификации банаховых пространств заключается в использовании вероятностного понятия типа и котипа : эти два параметра измеряют, насколько далеко банахово пространство находится от гильбертова пространства.

Базы дрожи

Основная статья: основа содрогания

База содрогания в банаховом пространстве $X$ это последовательность $\left\{e_{n}\right\}_{n\geq 0}$ векторов в $X$ со свойством, что для каждого вектора $x\in X,$ существуют однозначно определенные скаляры $\left\{x_{n}\right\}_{n\geq 0}$ в зависимости от $x,$ такой, что

$$x=\sum _{n=0}^{\infty }x_{n}e_{n},\quad {\textit {i.e.,}}\quad x=\lim _{n}P_{n}(x),\ P_{n}(x):=\sum _{k=0}^{n}x_{k}e_{k}.$$

Банаховы пространства с базисом Шаудера обязательно сепарабельны , поскольку счетное множество конечных линейных комбинаций с рациональными коэффициентами (скажем) плотно.

Из теоремы Банаха–Штайнхауза следует, что линейные отображения $\left\{P_{n}\right\}$ равномерно ограничены некоторой константой $C.$ Позволять $\left\{e_{n}^{*}\right\}$ обозначают координатные функционалы, которые присваиваются каждому $x$ в $X$ координата $x_{n}$ из $x$в приведенном выше расширении. Их называют биортогональными функционалами . Когда базисные векторы имеют норму $1,$ координатные функционалы $\left\{e_{n}^{*}\right\}$ есть норма $\,\leq 2C$ в дуале $X.$

Большинство классических сепарабельных пространств имеют явные базы. Система Хаара $\left\{h_{n}\right\}$ является основой для $L^{p}([0,1]),1\leq p<\infty .$ Тригонометрическая система является основой $L^{p}(\mathbf {T} )$ когда $1<p<\infty .$ Система Шаудера – основа в космосе $C([0,1]).$ Вопрос о том, существует ли дисковая алгебра $A(\mathbf {D} )$ имеет основу оставался открытым более сорока лет, пока Бочкарев в 1974 г. не показал, что $A(\mathbf {D} )$ допускает базис, построенный по системе Франклина .

Поскольку каждый вектор $x$ в банаховом пространстве $X$ с базисом – это предел $P_{n}(x),$ с $P_{n}$ конечного ранга и равномерно ограниченного, пространство $X$удовлетворяет свойству ограниченной аппроксимации . Первый пример Энфло пространства, не обладающего свойством аппроксимации, был в то же время первым примером сепарабельного банахового пространства без базиса Шаудера.

Роберт К. Джеймс охарактеризовал рефлексивность в банаховых пространствах с базисом: пространством $X$ с базисом Шаудера рефлексивно тогда и только тогда, когда базис одновременно сжимающийся и ограниченно полный . В этом случае биортогональные функционалы составляют основу двойственного $X.$

Тензорное произведение

Основные статьи: Тензорное произведение и Топологическое тензорное произведение.

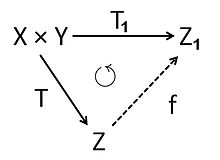
Позволять $X$ и $Y$ быть двумя $\mathbb {K}$-векторные пространства. Тензорное произведение $X\otimes Y$ из $X$ и $Y$ это $\mathbb {K}$-векторное пространство $Z$ с билинейным отображением $T:X\times Y\to Z$ который обладает следующим универсальным свойством :

Если $T_{1}:X\times Y\to Z_{1}$ – любое билинейное отображение в $\mathbb {K}$-векторное пространство $Z_{1},$ то существует единственное линейное отображение $f:Z\to Z_{1}$ такой, что $T_{1}=f\circ T.$

Изображение под $T$ из пары $(x,y)$ в $X\times Y$ обозначается $x\otimes y,$и называется простым тензором . Каждый элемент $z$ в $X\otimes Y$ является конечной суммой таких простых тензоров.

Существуют различные нормы, которые можно поместить в тензорное произведение основных векторных пространств, среди прочего проективная перекрестная норма и инъективная перекрестная норма , введенные А. Гротендиком в 1955 году.

В общем случае тензорное произведение полных пространств снова не является полным. При работе с банаховыми пространствами принято говорить, что проективное тензорное произведение двух банаховых пространств $X$ и $Y$ это завершение $X{\widehat {\otimes }}_{\pi }Y$ алгебраического тензорного произведения $X\otimes Y$ снабженный проективной тензорной нормой, и аналогично для инъективного тензорного произведения $X{\widehat {\otimes }}_{\varepsilon }Y.$ Гротендик, в частности, доказал, что

$${\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y),\end{aligned}}$$

где $K$ является компактным Хаусдорфовым пространством, $C(K,Y)$ банахово пространство непрерывных функций из $K$ к $Y$ и $L^{1}([0,1],Y)$ пространство измеримых по Бохнеру и интегрируемых функций из $[0,1]$ к $Y,$и где изоморфизмы изометричны. Два приведенных выше изоморфизма являются соответствующими расширениями отображения, отправляющего тензор $f\otimes y$ вектор-функции $s\in K\to f(s)y\in Y.$

аппроксимации

Позволять $X$быть банаховым пространством. Тензорное произведение $X'{\widehat {\otimes }}_{\varepsilon }X$ отождествляется изометрически с замыканием в $B(X)$множества операторов конечного ранга. Когда $X$ обладает свойством аппроксимации , это замыкание совпадает с пространством компактных операторов на $X.$

Для каждого банахова пространства $Y,$ есть естественная норма $1$ линейная карта

$$Y{\widehat {\otimes }}_{\pi }X\to Y{\widehat {\otimes }}_{\varepsilon }X$$

полученный путем расширения тождественного отображения алгебраического тензорного произведения. Гротендик связал проблему аппроксимации с вопросом о том, является ли это отображение взаимно однозначным, когда $Y$ является двойником $X.$ Точно, для любого банахова пространства $X,$ карта

$$X'{\widehat {\otimes }}_{\pi }X\ \longrightarrow X'{\widehat {\otimes }}_{\varepsilon }X$$

взаимно однозначно тогда и только тогда, когда $X$ обладает свойством аппроксимации.

Гротендик предположил, что $X{\widehat {\otimes }}_{\pi }Y$ и $X{\widehat {\otimes }}_{\varepsilon }Y$ должно быть разным, когда бы то ни было $X$ и $Y$являются бесконечномерными банаховыми пространствами. Это было опровергнуто Жилем Пизье в 1983 году. Пизье построил бесконечномерное банахово пространство. $X$ такой, что $X{\widehat {\otimes }}_{\pi }X$ и $X{\widehat {\otimes }}_{\varepsilon }X$равны. Более того, как и в примере Enflo , это пространство $X$— это «рукотворное» пространство, не обладающее свойством аппроксимации. С другой стороны, Шанковский доказал, что классическое пространство $B\left(\ell ^{2}\right)$ не обладает свойством аппроксимации.

результаты

гильбертова пространства среди

Необходимое и достаточное условие нормы банахова пространства. $X$ который должен быть связан с внутренним продуктом, - это тождество параллелограмма :

Параллелограммная идентичность — для всех $x,y\in X:\qquad \|x+y\|^{2}+\|x-y\|^{2}=2\left(\|x\|^{2}+\|y\|^{2}\right).$

Отсюда, например, следует, что пространство Лебега $L^{p}([0,1])$ является гильбертовым пространством только тогда, когда $p=2.$Если это тождество удовлетворено, соответствующий внутренний продукт определяется тождеством поляризации . В случае реальных скаляров это дает:

$$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}\right).$$

Для комплексных скаляров определение внутреннего продукта так, чтобы оно было $\mathbb {C}$-линейный по $x,$ антилинейный в $y,$ тождество поляризации дает:

$$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}+i\left(\|x+iy\|^{2}-\|x-iy\|^{2}\right)\right).$$

Чтобы убедиться в том, что закона параллелограмма достаточно, в реальном случае заметим, что $\langle x,y\rangle$ симметричен, а в сложном случае удовлетворяет свойству эрмитовой симметрии и $\langle ix,y\rangle =i\langle x,y\rangle .$ Из закона параллелограмма следует, что $\langle x,y\rangle$ является аддитивным в $x.$ Отсюда следует, что оно линейно относительно рациональных чисел, а значит, линейно по непрерывности.

Доступно несколько характеризаций пространств, изоморфных (а не изометрических) гильбертовым пространствам. Закон параллелограмма можно распространить на более чем два вектора и ослабить введением двустороннего неравенства с постоянной $c\geq 1$: Квапинь доказал, что если

$$c^{-2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}\leq \operatorname {Ave} _{\pm }\left\|\sum _{k=1}^{n}\pm x_{k}\right\|^{2}\leq c^{2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}$$

для каждого целого числа $n$ и все семейства векторов $\left\{x_{1},\ldots ,x_{n}\right\}\subseteq X,$ тогда банахово пространство $X$ изоморфно гильбертовому пространству. Здесь, $\operatorname {Ave} _{\pm }$ обозначает среднее значение за $2^{n}$ возможные варианты знаков $\pm 1.$ В той же статье Квапинь доказал, что справедливость банаховозначной теоремы Парсеваля для преобразования Фурье характеризует банаховые пространства, изоморфные гильбертовым пространствам.

Линденштраус и Цафрири доказали, что банахово пространство, в котором каждое замкнутое линейное подпространство дополнимо (т. е. является областью ограниченного линейного проектора), изоморфно гильбертовому пространству. Доказательство опирается на теорему Дворецкого о евклидовых сечениях многомерных центрально-симметричных выпуклых тел. Другими словами, теорема Дворецкого утверждает, что для любого целого числа $n,$ любое конечномерное нормированное пространство с размерностью, достаточно большой по сравнению с $n,$ содержит подпространства, почти изометричные $n$-мерное евклидово пространство.

Следующий результат дает решение так называемой проблемы однородного пространства . Бесконечномерное банахово пространство. $X$называется однородным, если оно изоморфно всем своим бесконечномерным замкнутым подпространствам. Банахово пространство, изоморфное $\ell ^{2}$ однородно, и Банах требовал обратного.

Теорема — Банахово пространство, изоморфное всем своим бесконечномерным замкнутым подпространствам, изоморфно сепарабельному гильбертовому пространству.

Бесконечномерное банахово пространство наследственно неразложимо, если ни одно его подпространство не может быть изоморфно прямой сумме двух бесконечномерных банаховых пространств. Гауэрса дихотомии Теорема о утверждает, что каждое бесконечномерное банахово пространство $X$ содержит либо подпространство $Y$ с безусловным базисом или наследственно неразложимым подпространством $Z,$ и в частности, $Z$ не изоморфна своим замкнутым гиперплоскостям. Если $X$является однородным, поэтому оно должно иметь безусловную основу. следует : Тогда из частного решения, полученного Коморовским и Томчаком–Егерманном , для пространств с безусловным базисом что $X$ изоморфен $\ell ^{2}.$

Метрическая

Если $T:X\to Y$ является изометрией банахова пространства $X$ в банахово пространство $Y$ (где оба $X$ и $Y$ являются векторными пространствами над $\mathbb {R}$), то теорема Мазура–Улама утверждает, что $T$должно быть аффинное преобразование. В частности, если $T(0_{X})=0_{Y},$ Это $T$ отображает ноль $X$ до нуля $Y,$ затем $T$должен быть линейным. Из этого результата следует, что метрика в банаховых пространствах и, в более общем смысле, в нормированных пространствах, полностью отражает их линейную структуру.

Топологическая

Конечномерные банаховы пространства гомеоморфны как топологические пространства тогда и только тогда, когда они имеют ту же размерность, что и вещественные векторные пространства.

Теорема Андерсона-Кадека (1965–66) доказывает что любые два бесконечномерных сепарабельных банаховых пространства гомеоморфны как топологические пространства. Теорема Кадеца была расширена Торунчиком, который доказал что любые два банаховых пространства гомеоморфны тогда и только тогда, когда они имеют одинаковый характер плотности — минимальную мощность плотного подмножества.

Пространства непрерывных функций

Когда два компакта Хаусдорфа $K_{1}$ и $K_{2}$ гомеоморфны , банаховы пространства $C\left(K_{1}\right)$ и $C\left(K_{2}\right)$являются изометрическими. И наоборот, когда $K_{1}$ не гомеоморфен $K_{2},$ (мультипликативное) расстояние Банаха – Мазура между $C\left(K_{1}\right)$ и $C\left(K_{2}\right)$ должно быть больше или равно $2,$см. выше результаты Амира и Камберна . Хотя несчетные компакты метрических пространств могут иметь разные типы гомеоморфии, Милютин дает следующий результат:

Теорема - Позволять $K$— несчетный компакт метрическое пространство. Затем $C(K)$ изоморфен $C([0,1]).$

Иная ситуация для счетно-бесконечных бикомпактов. Каждый счетный бесконечный компакт $K$ гомеоморфен некоторому замкнутому интервалу порядковых чисел

$$\langle 1,\alpha \rangle =\{\gamma \ :\ 1\leq \gamma \leq \alpha \}$$

оснащен порядковой топологией , где $\alpha$ является счетным бесконечным ординалом. Банахово пространство $C(K)$тогда изометричен C (⟨1, α ⟩) . Когда $\alpha ,\beta$ являются двумя счетными бесконечными ординалами, и предполагая $\alpha \leq \beta ,$ пространства C (⟨1, α ⟩) и C (⟨1, β ⟩) изоморфны тогда и только тогда, когда β < α ^ой . Например, банаховы пространства

$$C(\langle 1,\omega \rangle ),\ C(\langle 1,\omega ^{\omega }\rangle ),\ C(\langle 1,\omega ^{\omega ^{2}}\rangle ),\ C(\langle 1,\omega ^{\omega ^{3}}\rangle ),\cdots ,C(\langle 1,\omega ^{\omega ^{\omega }}\rangle ),\cdots$$

взаимно неизоморфны.

Примеры

Основная статья: Список банаховых пространств

Словарь символов для таблицы ниже:

• $\mathbb {F}$ обозначает поле действительных чисел $\mathbb {R}$ или комплексные числа $\mathbb {C} .$
• $K$ — компактное хаусдорфово пространство .
• $p,q\in \mathbb {R}$ действительные числа с $1<p,q<\infty$ которые являются сопряженными по Гельдеру , что означает, что они удовлетворяют ${\frac {1}{q}}+{\frac {1}{p}}=1$ и поэтому также $q={\frac {p}{p-1}}.$
• $\Sigma$ это $\sigma$-алгебра множеств.
• $\Xi$ является алгеброй множеств (для пространств, требующих только конечной аддитивности, таких как пространство ba ).
• $\mu$ это мера с вариацией $|\mu |.$ Положительная мера — это вещественная положительная функция множества, определенная на $\sigma$-алгебра, счетно-аддитивная.

Классические банаховы пространства
	Двойное пространство	Рефлексивный	слабо последовательно завершенный	Норма		Примечания
$\mathbb {F} ^{n}$	$\mathbb {F} ^{n}$	Да	Да	$\|x\|_{2}$	$=\left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}$	Евклидово пространство
$\ell _{p}^{n}$	$\ell _{q}^{n}$	Да	Да	$\|x\|_{p}$	$=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{\frac {1}{p}}$
$\ell _{\infty }^{n}$	$\ell _{1}^{n}$	Да	Да	$\|x\|_{\infty }$	$=\max \nolimits _{1\leq i\leq n}|x_{i}|$
$\ell ^{p}$	$\ell ^{q}$	Да	Да	$\|x\|_{p}$	$=\left(\sum _{i=1}^{\infty }|x_{i}|^{p}\right)^{\frac {1}{p}}$
$\ell ^{1}$	$\ell ^{\infty }$	Нет	Да	$\|x\|_{1}$	$=\sum _{i=1}^{\infty }\left|x_{i}\right|$
$\ell ^{\infty }$	$\operatorname {ba}$	Нет	Нет	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$
$\operatorname {c}$	$\ell ^{1}$	Нет	Нет	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$
$c_{0}$	$\ell ^{1}$	Нет	Нет	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$	Изоморфен, но не изометричен $c.$
$\operatorname {bv}$	$\ell ^{\infty }$	Нет	Да	$\|x\|_{bv}$	$=\left|x_{1}\right|+\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|$	Изометрически изоморфен $\ell ^{1}.$
$\operatorname {bv} _{0}$	$\ell ^{\infty }$	Нет	Да	$\|x\|_{bv_{0}}$	$=\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|$	Изометрически изоморфен $\ell ^{1}.$
$\operatorname {bs}$	$\operatorname {ba}$	Нет	Нет	$\|x\|_{bs}$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|$	Изометрически изоморфен $\ell ^{\infty }.$
$\operatorname {cs}$	$\ell ^{1}$	Нет	Нет	$\|x\|_{bs}$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|$	Изометрически изоморфен $c.$
$B(K,\Xi )$	$\operatorname {ba} (\Xi )$	Нет	Нет	$\|f\|_{B}$	$=\sup \nolimits _{k\in K}|f(k)|$
$C(K)$	$\operatorname {rca} (K)$	Нет	Нет	$\|x\|_{C(K)}$	$=\max \nolimits _{k\in K}|f(k)|$
$\operatorname {ba} (\Xi )$	?	Нет	Да	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$
$\operatorname {ca} (\Sigma )$	?	Нет	Да	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$	Замкнутое подпространство $\operatorname {ba} (\Sigma ).$
$\operatorname {rca} (\Sigma )$	?	Нет	Да	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$	Замкнутое подпространство $\operatorname {ca} (\Sigma ).$
$L^{p}(\mu )$	$L^{q}(\mu )$	Да	Да	$\|f\|_{p}$	$=\left(\int |f|^{p}\,d\mu \right)^{\frac {1}{p}}$
$L^{1}(\mu )$	$L^{\infty }(\mu )$	Нет	Да	$\|f\|_{1}$	$=\int |f|\,d\mu$	Двойник - это $L^{\infty }(\mu )$ если $\mu$ является $\sigma$-конечный .
$\operatorname {BV} ([a,b])$	?	Нет	Да	$\|f\|_{BV}$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)$	$V_{f}([a,b])$ это вариация полная $f$
$\operatorname {NBV} ([a,b])$	?	Нет	Да	$\|f\|_{BV}$	$=V_{f}([a,b])$	$\operatorname {NBV} ([a,b])$ состоит из $\operatorname {BV} ([a,b])$ функции такие, что $\lim \nolimits _{x\to a^{+}}f(x)=0$
$\operatorname {AC} ([a,b])$	$\mathbb {F} +L^{\infty }([a,b])$	Нет	Да	$\|f\|_{BV}$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)$	Изоморфно пространству Соболева. $W^{1,1}([a,b]).$
$C^{n}([a,b])$	$\operatorname {rca} ([a,b])$	Нет	Нет	$\|f\|$	$=\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|$	Изоморфен $\mathbb {R} ^{n}\oplus C([a,b]),$ по сути, по теореме Тейлора .

Производные

В банаховом пространстве можно определить несколько понятий производной. см. в статьях о производной Фреше и производной Гато Подробности . Производная Фреше позволяет расширить концепцию полной производной на банаховы пространства. Производная Гато позволяет расширить производную по направлению на локально выпуклые топологические векторные пространства . Дифференцируемость по Фреше является более сильным условием, чем дифференцируемость по Гато. Квазипроизводная . — это еще одно обобщение производной по направлению, которое подразумевает более сильное условие, чем дифференцируемость Гато, но более слабое условие, чем дифференцируемость по Фреше

Обобщения

Несколько важных пространств функционального анализа, например пространство всех бесконечно часто дифференцируемых функций. $\mathbb {R} \to \mathbb {R} ,$ или пространство всех распределений на $\mathbb {R} ,$полны, но не являются нормированными векторными пространствами и, следовательно, не банаховыми пространствами. В пространствах Фреше еще имеется полная метрика , тогда как LF-пространства представляют собой полные равномерные векторные пространства, возникающие как пределы пространств Фреше.

См. также

• Пространство (математика) - математический набор с некоторой дополнительной структурой.
  • Пространство Фреше - локально выпуклое топологическое векторное пространство, которое также является полным метрическим пространством.
  • Пространство Харди – концепция комплексного анализа
  • Гильбертово пространство - тип топологического векторного пространства.
  • L-полувнутренний продукт - обобщение внутренних произведений, применимое ко всем нормированным пространствам.
  • $L^{p}$ пространство - функциональные пространства, обобщающие конечномерные пространства с нормой p.
  • Пространство Соболева - Векторное пространство функций в математике.
  • Банахова решетка - банахово пространство с совместимой структурой решетки.
• Банахов диск
• Банахово многообразие - Многообразие, смоделированное на банаховых пространствах.
  • Банахово расслоение - векторное расслоение, слои которого образуют банахово пространство. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Проблема искажений
• Интерполяционное пространство
• Локально выпуклое топологическое векторное пространство - векторное пространство с топологией, определяемой выпуклыми открытыми множествами.
• Модуль и характеристика выпуклости
• Пространство Смита - полное компактно сгенерированное локально выпуклое пространство, имеющее универсальный компактный набор. Страницы, отображающие описания викиданных в качестве запасного варианта.
• Топологическое векторное пространство - векторное пространство с понятием близости.
• Пространство Цирельсона

Библиография

• Алипрантис, Хараламбос Д .; Бордер, Ким К. (2006). Бесконечномерный анализ: Путеводитель для путешествующих автостопом (Третье изд.). Берлин: Springer Science & Business Media. ISBN  978-3-540-29587-7 . OCLC   262692874 .
• Андерсон, РД; Шори, Р. (1969). «Факторы бесконечномерных многообразий» (PDF) . Труды Американского математического общества . 142 . Американское математическое общество (AMS): 315–330. дои : 10.1090/s0002-9947-1969-0246327-5 . ISSN   0002-9947 .
• Бахман, Джордж; Наричи, Лоуренс (2000). Функциональный анализ (Второе изд.). Минеола, Нью-Йорк: Dover Publications. ISBN  978-0486402512 . OCLC   829157984 .
• Банах, Стефан (1932). Théorie des Opérations Lineaires [ Теория линейных операций ] (PDF) . Математические монографии (на французском языке). Том 1. Варшава: Субсидии Фонда национальной культуры. Збл   0005.20901 . Архивировано из оригинала (PDF) 11 января 2014 г. Проверено 11 июля 2020 г.
• Бозами, Бернар (1985) [1982], Введение в банаховые пространства и их геометрию (второе исправленное издание), Северная Голландия .* Бурбаки, Николя (1987) [1981]. Топологические векторные пространства: главы 1–5 . Элементы математики . Перевод Эгглстона, Х.Г.; Мадан, Южный Берлин, Нью-Йорк: Springer-Verlag. ISBN  3-540-13627-4 . OCLC   17499190 .
• Бессага, К.; Пелчинский, А. (1975), Избранные темы бесконечномерной топологии , Monografie Matematyczne, Варшава: Panstwowe ed. научный .
• Карозерс, Нил Л. (2005), Краткий курс по теории банахового пространства , Тексты для студентов Лондонского математического общества, том. 64, Кембридж: Издательство Кембриджского университета, стр. xii+184, ISBN  0-521-84283-2 .
• Конвей, Джон (1990). Курс функционального анализа . Тексты для выпускников по математике Том. 96 (2-е изд.). Нью-Йорк: Springer-Publishing . ISBN  978-0-387-97245-9 . OCLC   21195908 .
• Дистель, Джозеф (1984), Последовательности и ряды в банаховых пространствах , Тексты для аспирантов по математике, том. 92, Нью-Йорк: Springer-Publishers, стр. 101–116. xii+261 , ISBN  0-387-90859-5 .
• Данфорд, Нельсон; Шварц, Джейкоб Т. при содействии В.Г. Бэйда и Р.Г. Бартла (1958), Линейные операторы. I. Общая теория , Чистая и прикладная математика, вып. 7, Нью-Йорк: Interscience Publishers, Inc., MR   0117523.
• Эдвардс, Роберт Э. (1995). Функциональный анализ: теория и приложения . Нью-Йорк: Dover Publications. ISBN  978-0-486-68143-6 . ОСЛК   30593138 .
• Гротендик, Александр (1973). Топологические векторные пространства . Перевод Чалджуба, Орландо. Нью-Йорк: Издательство Gordon and Breach Science. ISBN  978-0-677-30020-7 . OCLC   886098 .
• Хендерсон, Дэвид В. (1969). «Бесконечномерные многообразия являются открытыми подмножествами гильбертова пространства» . Бык. амер. Математика. Соц . 75 (4): 759–762. дои : 10.1090/S0002-9904-1969-12276-7 . МР   0247634 .
• Халилулла, С.М. (1982). Контрпримеры в топологических векторных пространствах Конспект лекций по математике . Том. 936. Берлин, Гейдельберг, Нью-Йорк: Springer-Verlag . ISBN  978-3-540-11565-6 . OCLC   8588370 .
• Линденштраусс, Йорам ; Цафрири, Лиор (1977), Классические банаховы пространства I, Пространства последовательностей , Результаты математики и ее границ, том. 92, Берлин: Springer-Verlag, ISBN.  3-540-08072-4 .
• Меггинсон, Роберт Э. (1998), Введение в теорию банахового пространства , Тексты для аспирантов по математике, том. 183, Нью-Йорк: Springer-Verlag, стр. xx+596, ISBN.  0-387-98431-3 .
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN  978-1584888666 . OCLC   144216834 .
• Рисс, Фредерик ; Сз.-Надь, Белла (1990) [1955]. Функциональный анализ . Перевод Борона, Лео Ф. Нью-Йорк: Dover Publications ISBN  0-486-66289-6 . OCLC   21228994 .
• Рудин, Вальтер (1991). Функциональный анализ . Международная серия по чистой и прикладной математике. Том. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN  978-0-07-054236-5 . OCLC   21163277 .
• Райан, Раймонд А. (2002), Введение в тензорные произведения банаховых пространств , Монографии Спрингера по математике, Лондон: Springer-Verlag, стр. xiv + 225, ISBN  1-85233-437-1 .
• Шефер, Хельмут Х .; Вольф, Манфред П. (1999). Топологические векторные пространства . ГТМ . Том. 8 (Второе изд.). Нью-Йорк, Нью-Йорк: Springer New York Выходные данные Springer. ISBN  978-1-4612-7155-0 . OCLC   840278135 .
• Шварц, Чарльз (1992). Введение в функциональный анализ . Нью-Йорк: М. Деккер. ISBN  978-0-8247-8643-4 . ОСЛК   24909067 .
• Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC   853623322 .
• Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
• Wojtaszczyk, Przemysław (1991), Banach spaces for analysts, Cambridge Studies in Advanced Mathematics, vol. 25, Cambridge: Cambridge University Press, pp. xiv+382, ISBN 0-521-35618-0.

External links

• "Banach space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Banach Space". MathWorld.