Выпуклая комбинация

Учитывая три очка $x_{1},x_{2},x_{3}$ в плоскости, как показано на рисунке, точка $P$ представляет собой выпуклую комбинацию трех точек, а $Q$ нет ​ .

( $Q$ однако является аффинной комбинацией трех точек, поскольку их аффинной оболочкой является вся плоскость.)

Выпуклая комбинация двух точек $v_{1},v_{2}\in \mathbb {R} ^{2}$ в двумерном векторном пространстве $\mathbb {R} ^{2}$ как анимация в Geogebra с $t\in [0,1]$ и $K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}$

Выпуклая комбинация трех точек $v_{0},v_{1},v_{2}{\text{ of }}2{\text{-simplex}}\in \mathbb {R} ^{2}$ в двумерном векторном пространстве $\mathbb {R} ^{2}$ как показано в анимации с $\alpha ^{0}+\alpha ^{1}+\alpha ^{2}=1$, $P(\alpha ^{0},\alpha ^{1},\alpha ^{2})$ $:=\alpha ^{0}v_{0}+\alpha ^{1}v_{1}+\alpha ^{2}v_{2}$ . Когда P находится внутри треугольника $\alpha _{i}\geq 0$. В противном случае, когда P находится вне треугольника, хотя бы один из $\alpha _{i}$ является отрицательным.

Выпуклая комбинация из четырех точек $A_{1},A_{2},A_{3},A_{4}\in \mathbb {R} ^{3}$ в трехмерном векторном пространстве $\mathbb {R} ^{3}$ как анимация в Geogebra с $\sum _{i=1}^{4}\alpha _{i}=1$ и $\sum _{i=1}^{4}\alpha _{i}\cdot A_{i}=P$. Когда P находится внутри тетраэдра $\alpha _{i}>=0$. В противном случае, когда P находится вне тетраэдра, хотя бы один из $\alpha _{i}$ является отрицательным.

Выпуклая комбинация двух функций как векторов в векторном пространстве функций - визуализирована в Open Source Geogebra с помощью $[a,b]=[-4,7]$ и в качестве первой функции $f:[a,b]\to \mathbb {R}$ полином определен. $f(x):={\frac {3}{10}}\cdot x^{2}-2$ Тригонометрическая функция $g:[a,b]\to \mathbb {R}$ была выбрана в качестве второй функции. $g(x):=2\cdot \cos(x)+1$ На рисунке изображена выпуклая комбинация $K(t):=(1-t)\cdot f+t\cdot g$ из $f$ и $g$ в виде графика красного цвета.

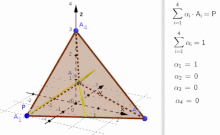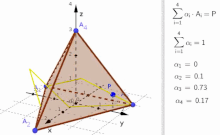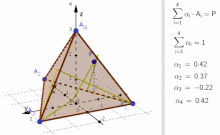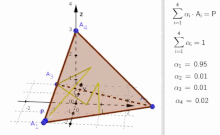
В выпуклой геометрии и векторной алгебре выпуклая комбинация — это линейная комбинация точек и в сумме (которые могут быть векторами , скалярами или, в более общем плане, точками в аффинном пространстве где все коэффициенты неотрицательны ) , равны 1. Другими словами, операция эквивалентна стандартному средневзвешенному значению , но веса которого выражаются в процентах от общего веса, а не в долях от количества весов , как в стандартном средневзвешенном значении.

Формальное определение

Более формально, учитывая конечное число точек $x_{1},x_{2},\dots ,x_{n}$ в реальном векторном пространстве выпуклая комбинация этих точек есть точка вида

$\alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}$

где реальные цифры $\alpha _{i}$ удовлетворить $\alpha _{i}\geq 0$ и $\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}=1.$

Например, каждая выпуклая комбинация двух точек лежит на отрезке между этими точками.

Множество называется выпуклым , если оно содержит все выпуклые комбинации своих точек.Выпуклая оболочка данного набора точек идентична множеству всех их выпуклых комбинаций.

Существуют подмножества векторного пространства, не замкнутые относительно линейных комбинаций, но замкнутые относительно выпуклых комбинаций. Например, интервал $[0,1]$ является выпуклым, но генерирует линию действительных чисел при линейных комбинациях. Другим примером является выпуклое множество вероятностных распределений , поскольку линейные комбинации не сохраняют ни неотрицательности, ни аффинности (т. е. имеют полную интегральную единицу).

Другие объекты

• Случайная величина $X$ говорят, что есть $n$-компонентное конечное распределение смеси , если ее функция плотности вероятности представляет собой выпуклую комбинацию $n$ так называемые плотности компонентов.

Родственные конструкции

Дополнительная информация: Линейная комбинация § Аффинные, конические и выпуклые комбинации.

• Коническая комбинация — это линейная комбинация с неотрицательными коэффициентами. Когда точка $x$ будет использоваться в качестве исходной точки для определения векторов смещения , затем $x$ представляет собой выпуклую комбинацию $n$ очки $x_{1},x_{2},\dots ,x_{n}$ тогда и только тогда, когда нулевое перемещение представляет собой нетривиальную коническую комбинацию их $n$ соответствующие векторы смещения относительно $x$.
• Взвешенные средние функционально аналогичны выпуклым комбинациям, но в них используются другие обозначения. Коэффициенты ( веса ) средневзвешенного значения не обязаны давать в сумме 1; вместо этого взвешенная линейная комбинация явно делится на сумму весов.
• Аффинные комбинации подобны выпуклым комбинациям, но коэффициенты не обязательно должны быть неотрицательными. Следовательно, аффинные комбинации определяются в векторных пространствах над любым полем .

См. также

• Аффинная оболочка
• Теорема Каратеодори (выпуклая оболочка)
• Симплекс
• Барицентрическая система координат
• Выпуклое пространство

Внешние ссылки

• Выпуклая сумма/комбинация с треугольником — интерактивная иллюстрация
• Выпуклая сумма/комбинация с шестиугольником - интерактивная иллюстрация
• Выпуклая сумма/комбинация с тетраэдром - интерактивная иллюстрация