Полином Джонса

В математической области теории узлов полином Джонса — это полином узлов, открытый Воаном Джонсом в 1984 году. В частности, это инвариант ориентированного узла или звена , который присваивает каждому ориентированному узлу или звену полином Лорана от переменной $t^{1/2}$ с целыми коэффициентами.

Определение в скобках

Тип I ход Рейдемейстера

Предположим, у нас есть ориентированная ссылка $L$, заданный в виде диаграммы узла . Определим полином Джонса $V(L)$ используя Луи Кауфмана , скобочный многочлен который мы обозначаем через $\langle ~\rangle$. Здесь скобочный полином является полиномом Лорана от переменной $A$ с целыми коэффициентами.

Сначала мы определяем вспомогательный многочлен (также известный как многочлен нормализованной скобки)

$X(L)=(-A^{3})^{-w(L)}\langle L\rangle ,$

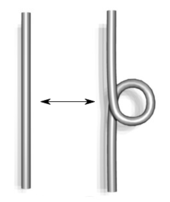
где $w(L)$ обозначает корчи ​ $L$ на данной диаграмме. Искривление диаграммы — это количество положительных пересечений ( $L_{+}$ на рисунке ниже) минус количество отрицательных пересечений ( $L_{-}$). Корчи не являются инвариантом узла.

$X(L)$ является инвариантом узла, так как он инвариантен относительно изменений диаграммы $L$ тремя ходами Рейдемейстера . Инвариантность относительно ходов Райдемейстера II и III типов следует из инвариантности скобки относительно этих ходов. Известно, что скобочный полином изменяется в раз. $-A^{\pm 3}$ под ходом Рейдемейстера типа I. Определение $X$ полином, приведенный выше, предназначен для того, чтобы свести на нет это изменение, поскольку корчи изменяются соответствующим образом на $+1$ или $-1$ по типу I движется.

Теперь сделайте замену $A=t^{-1/4}$ в $X(L)$ чтобы получить полином Джонса $V(L)$. В результате получается полином Лорана с целыми коэффициентами в переменной $t^{1/2}$.

Полином Джонса для клубков

Эта конструкция полинома Джонса для клубков является простым обобщением скобки Кауфмана зацепления. Конструкция была разработана Владимиром Тураевым и опубликована в 1990 году.

Позволять $k$ быть неотрицательным целым числом и $S_{k}$ обозначают набор всех изотопных типов диаграмм клубка, где $2k$ концов, не имеющих точек пересечения и замкнутых компонент (сглаживаний). Конструкция Тураева использует предыдущую конструкцию скобки Кауфмана и сопоставляет каждой $2k$-ориентированный на конец клубок, элемент свободного $\mathrm {R}$-модуль $\mathrm {R} [S_{k}]$, где $\mathrm {R}$ — кольцо с полиномов Лорана целыми коэффициентами от переменной $t^{1/2}$.

Определение по представлению косы

Первоначальная формулировка своего полинома Джонсом возникла в результате его изучения операторных алгебр. В подходе Джонса оно возникло в результате своего рода «следа» конкретного представления косы в алгебре, первоначально возникшего при изучении определенных моделей, например модели Поттса , в статистической механике .

ссылка L. Пусть дана Теорема Александера утверждает, что это замыкание следа косы, скажем, из n нитей. Теперь определим представление $\rho$ группы кос на n нитях B _n в алгебру Темперли–Либа $\operatorname {TL} _{n}$ с коэффициентами в $\mathbb {Z} [A,A^{-1}]$ и $\delta =-A^{2}-A^{-2}$. Стандартный генератор кос $\sigma _{i}$ отправляется в $A\cdot e_{i}+A^{-1}\cdot 1$, где $1,e_{1},\dots ,e_{n-1}$ являются стандартными генераторами алгебры Темперли–Либа. Легко проверить, что это определяет представление.

Возьми слово о косе $\sigma$ полученный ранее от $L$ и вычислить $\delta ^{n-1}\operatorname {tr} \rho (\sigma )$ где $\operatorname {tr}$ это марковский след . Это дает $\langle L\rangle$, где $\langle$ $\rangle$ – скобочный полином. В этом можно убедиться, рассматривая, как это сделал Луи Кауфман , алгебру Темперли – Либа как особую диаграммную алгебру.

Преимущество этого подхода состоит в том, что можно выбрать подобные представления в других алгебрах, таких как представления R -матрицы, что приводит к «обобщенным инвариантам Джонса».

Свойства

Полином Джонса характеризуется тем, что принимает значение 1 на любой диаграмме узла и удовлетворяет следующему соотношению мотка :

$(t^{1/2}-t^{-1/2})V(L_{0})=t^{-1}V(L_{+})-tV(L_{-})\,$

где $L_{+}$, $L_{-}$, и $L_{0}$ представляют собой три диаграммы ориентированных связей, которые идентичны, за исключением одной небольшой области, где они отличаются изменениями пересечения или сглаживанием, показанными на рисунке ниже:

Определение полинома Джонса скобкой позволяет легко показать, что для узла $K$, полином Джонса его зеркального отображения определяется заменой $t^{-1}$ для $t$ в $V(K)$. Таким образом, амфихейральный узел , узел, эквивалентный своему зеркальному изображению, имеет палиндромные элементы в своем полиноме Джонса. См. статью о соотношении мотков , где приведен пример вычислений с использованием этих отношений.

Другое замечательное свойство этого инварианта гласит, что полином Джонса переменного звена является переменным полиномом . Это свойство было подтверждено Морвен Тистлтуэйт. в 1987 году. Другое доказательство этого последнего свойства принадлежит Эрнандо Бургос-Сото , который также дал расширение клубков собственности.

Полином Джонса не является полным инвариантом. Существует бесконечное количество неэквивалентных узлов, имеющих один и тот же полином Джонса. Пример двух разных узлов, имеющих одинаковый полином Джонса, можно найти в книге Мурасуги.

Джонса

Для положительного целого числа $N$, $N$-цветной полином Джонса $V_{N}(L,t)$ является обобщением полинома Джонса. Это инвариант Решетихина–Тураева, связанный с $(N+1)$-неприводимое представление квантовой группы $U_{q}({\mathfrak {sl}}_{2})$. В этой схеме полином Джонса — это одноцветный полином Джонса, инвариант Решетихина-Тураева, связанный со стандартным представлением (неприводимым и двумерным) $U_{q}({\mathfrak {sl}}_{2})$. Считается, что нити ссылки «окрашены» представлением, отсюда и название.

В общем, учитывая ссылку $L$ из $k$ компоненты и представления $V_{1},\ldots ,V_{k}$ из $U_{q}({\mathfrak {sl}}_{2})$, $(V_{1},\ldots ,V_{k})$-цветной полином Джонса $V_{V_{1},\ldots ,V_{k}}(L,t)$ – инвариант Решетихина–Тураева, связанный с $V_{1},\ldots ,V_{k}$ (здесь мы предполагаем, что компоненты упорядочены). Учитывая два представления $V$ и $W$, цветные полиномы Джонса удовлетворяют следующим двум свойствам:

• $V_{V\oplus W}(L,t)=V_{V}(L,t)+V_{W}(L,t)$,
• $V_{V\otimes W}(L,t)=V_{V,W}(L^{2},t)$, где $L^{2}$ обозначает 2-кабельное соединение $L$.

Эти свойства вытекают из того, что цветные полиномы Джонса являются инвариантами Решетихина-Тураева.

Позволять $K$ быть узлом. Напомним, что, рассматривая диаграмму $K$ как элемент алгебры Темперли-Либа благодаря скобке Кауфмана восстанавливается полином Джонса $K$. Аналогичным образом, $N$-цветной полином Джонса $K$ может быть дано комбинаторное описание с использованием идемпотентов Джонса-Венцля следующим образом:

• рассмотреть $N$-кабеля $K^{N}$ из $K$;
• рассматривать его как элемент алгебры Темперли-Либа;
• вставьте идемпотенты Джонса-Венцля в некоторые $N$ параллельные пряди.

Полученный элемент $\mathbb {Q} (t)$ это $N$-цветной полином Джонса. См. приложение H для получения более подробной информации.

с

Черна –

Как впервые показал Эдвард Виттен , полином Джонса данного узла $\gamma$ можно получить, рассматривая теорию Черна–Саймонса на трехсфере с калибровочной группой $\mathrm {SU} (2)$и вычисление вакуумного среднего значения петли Вильсона $W_{F}(\gamma )$, связанный с $\gamma$и фундаментальное представление $F$ из $\mathrm {SU} (2)$.

с инвариантами

Подставив $e^{h}$ для переменной $t$ полинома Джонса и разложив его в ряд h, каждый из коэффициентов оказывается инвариантом Васильева узла $K$. Чтобы унифицировать инварианты Васильева (или инварианты конечного типа), Максим Концевич построил интеграл Концевича . Значение интеграла Концевича, представляющего собой бесконечную сумму 1,3-значных хордовых диаграмм , называемых хордовыми диаграммами Якоби, воспроизводит полином Джонса вместе с ${\mathfrak {sl}}_{2}$ Система весов, изученная Дрором Бар-Натаном .

Связь с гипотезой объема

Путем численного исследования некоторых гиперболических узлов Ринат Кашаев обнаружил, что, подставив корень n -й степени из единицы в параметр цветного полинома Джонса, соответствующий n -мерному представлению, и ограничив его при возрастании n до бесконечности, предельное значение даст гиперболический объем узла дополнения . (См. Гипотезу об объеме .)

с

В 2000 году Михаил Хованов построил некоторый цепной комплекс узлов и звеньев и показал, что индуцированные из него гомологии являются инвариантом узла (см. Гомологии Хованова ). Полином Джонса описывается как эйлерова характеристика этой гомологии.

Обнаружение узла

Вопрос о том, существует ли нетривиальный узел с полиномом Джонса, равным полиному Джонса, остается открытым . Известно, что существуют нетривиальные связи с полиномом Джонса, равные соответствующим развязкам по работе Морвена Тистлтуэйта . Кронхаймер и Мровка показали, что не существует нетривиального узла с гомологией Хованова, равной гомологии неузла.

См. также

• Полином ХОМФЛИ
• полином Александера
• Гипотеза об объеме
• Chern–Simons theory
• Квантовая группа

Ссылки

• Адамс, Колин (6 декабря 2000 г.). Книга Узелка . Американское математическое общество . ISBN  0-8050-7380-9 .
• Джонс, Вон . «Полином Джонса» (PDF) .
• Джонс, Воган (1987). «Представления в алгебре Гекке групп кос и полиномов зацепления». Анналы математики . 126 (2): 335–388. дои : 10.2307/1971403 . JSTOR   1971403 .
• Кауфман, Луи Х. (1987). «Модели состояний и полином Джонса» . Топология . 26 (3): 395–407. дои : 10.1016/0040-9383(87)90009-7 . (объясняет определение с помощью полинома в скобках и его связь с формулировкой Джонса с помощью представления косы)
• Ликориш, В.Б. Рэймонд (1997). Введение в теорию узлов . Нью-Йорк; Берлин; Гейдельберг; Барселона; Будапешт; Гонконг; Лондон; Милан; Париж; Санта-Клара; Сингапур; Токио: Спрингер. п. 175. ИСБН  978-0-387-98254-0 .
• Тистлтуэйт, Морвен (2001). «Связи с тривиальным полиномом Джонса». Журнал теории узлов и ее разветвлений . 10 (4): 641–643. дои : 10.1142/S0218216501001050 .
• Элиаху, Шалом; Кауфман, Луи Х .; Тистлтуэйт, Морвен Б. (2003). «Бесконечные семейства зацеплений с тривиальным полиномом Джонса» . Топология . 42 (1): 155–169. дои : 10.1016/S0040-9383(02)00012-5 .
• Пшитицкий, Юзеф Х. (1991). «Модули мотков трехмерных многообразий». Вестник Польской академии наук . 39 (1–2): 91–100. arXiv : math/0611797 .

Внешние ссылки

• «Полином Джонса-Конвея» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Ссылки на тривиальный полином Джонса Морвен Тистлтуэйт
• « Полином Джонса », Атлас узлов .