Торовый узел

Не путать с Торусом .

(3,−7) -3D торический узел.

Премия EureleA за изображение (2,3)-тора узла.

(2,8) звено тора

В теории узлов — торический узел это особый вид узла , лежащий на поверхности незавязанного тора в R. ³ . Аналогично, звено тора — это звено , лежащее на поверхности тора таким же образом. Каждый торический узел задается парой взаимно простых целых чисел p и q . Зацепление тора возникает, если p и q не взаимно просты (в этом случае число компонентов равно НОД ( p, q )). Торический узел тривиален (эквивалентен неузелку) тогда и только тогда, когда либо p , либо q равны 1 или −1. Простейшим нетривиальным примером является (2,3)-торический узел, также известный как узел-трилистник .

(2,−3)-торический узел, также известный как левый узел-трилистник

Геометрическое представление

Торический узел можно отобразить геометрически несколькими способами, которые топологически эквивалентны (см. «Свойства» ниже), но геометрически различны. В этой статье и ее рисунках используется следующее соглашение.

( p , q )-торический узел обматывает q раз вокруг круга внутри тора и p раз вокруг своей оси вращательной симметрии . . Если p и q не взаимно просты, то мы имеем торическое звено с более чем одним компонентом.

Направление, в котором нити узла обвивают тор, также регулируется различными соглашениями. Чаще всего нити образуют правосторонний винт при pq > 0 .

( p , q )-торический узел можно задать параметризацией

${\begin{aligned}x&=r\cos(p\phi )\\y&=r\sin(p\phi )\\z&=-\sin(q\phi )\end{aligned}}$

где $r=\cos(q\phi )+2$ и $0<\phi <2\pi$. Оно лежит на поверхности тора, заданного формулой $(r-2)^{2}+z^{2}=1$ (в цилиндрических координатах ).

Возможны и другие параметризации, поскольку узлы определяются с точностью до непрерывной деформации. Иллюстрации для (2,3)- и (3,8)-торических узлов можно получить, взяв $r=\cos(q\phi )+4$, а в случае (2,3)-торического узла дополнительно вычитая соответственно $3\cos((p-q)\phi )$ и $3\sin((p-q)\phi )$ из приведенных выше параметризаций x и y . Последнее гладко обобщается на любые взаимно простые p,q, удовлетворяющие $p<q<2p$.

Характеристики

Схема (3,−8)-торического узла.

Торический узел тривиален тогда и только тогда, когда либо p , либо q равны 1 или −1.

Каждый нетривиальный торический узел является простым. и хиральный .

Торический узел ( p , q ) эквивалентен торическому узлу ( q , p ). Это можно доказать, перемещая нити по поверхности тора. Торический узел ( p ,− q ) является лицевой стороной (зеркальным изображением) торического узла ( p , q ). Торический узел (− p ,− q ) эквивалентен торическому узлу ( p , q ), за исключением обратной ориентации.

Торический узел (3, 4) на развернутой поверхности тора и слово его косы

Любой ( p , q )-торический узел можно сделать из замкнутой косы с p нитями. Подходящее слово для косы —

$(\sigma _{1}\sigma _{2}\cdots \sigma _{p-1})^{q}.$

(Эта формула предполагает общепринятое соглашение о том, что генераторы кос представляют собой правые скручивания, за которым не следует страница Википедии о косах.)

Число пересечений торического узла ( p , q ) с p , q > 0 определяется выражением

c знак равно min(( п -1) q , ( q -1) п ).

Род > торического узла с , q p 0 равен

$g={\frac {1}{2}}(p-1)(q-1).$

Полином Александера торического узла равен

$t^{k}{\frac {(t^{pq}-1)(t-1)}{(t^{p}-1)(t^{q}-1)}},$ где $k=-{\frac {(p-1)(q-1)}{2}}.$

Полином Джонса (правого) торического узла имеет вид

$t^{(p-1)(q-1)/2}{\frac {1-t^{p+1}-t^{q+1}+t^{p+q}}{1-t^{2}}}.$

Дополнением к торическому узлу в 3-сфере является многообразие Зейферта , расслоенное над диском двумя особыми слоями.

Пусть Y — p -кратная дурацкая шапочка с удаленным изнутри диском, Z — q -кратная дурацкая шапка с удаленным изнутри диском, а X — фактор-пространство, полученное путем отождествления Y и Z вдоль их граничного круга. Узловое дополнение деформации узла ( , q ) -тора втягивается в пространство X. p Поэтому группа узлов торического узла имеет представление

$\langle x,y\mid x^{p}=y^{q}\rangle .$

Торические узлы — единственные узлы, группы узлов которых имеют нетривиальный центр (который является бесконечным циклическим, порожденным элементом $x^{p}=y^{q}$ в презентации выше).

Коэффициент растяжения торического узла ( p , q ), как кривой в евклидовом пространстве , равен Ω(min( p , q )), поэтому торические узлы имеют неограниченные коэффициенты растяжения. Студент-исследователь Джон Пардон получил премию Моргана 2012 года за исследование, доказывающее этот результат, который решил проблему, первоначально поставленную Михаилом Громовым .

Подключение к сложным гиперповерхностям

( p , q )-торические узлы возникают при рассмотрении зацепления изолированной комплексной гиперповерхностной особенности. Комплексную гиперповерхность пересекают гиперсферой с центром в изолированной особой точке и достаточно малым радиусом, так что она не охватывает и не сталкивается с какими-либо другими особыми точками. Пересечение дает подмногообразие гиперсферы.

Пусть p и q — взаимно простые целые числа, большие или равные двум. Рассмотрим голоморфную функцию $f:\mathbb {C} ^{2}\to \mathbb {C}$ данный $f(w,z):=w^{p}+z^{q}.$ Позволять $V_{f}\subset \mathbb {C} ^{2}$ быть набором $(w,z)\in \mathbb {C} ^{2}$ такой, что $f(w,z)=0.$ Учитывая действительное число $0<\varepsilon \ll 1,$ мы определяем реальную трехсферу $\mathbb {S} _{\varepsilon }^{3}\subset \mathbb {R} ^{4}\hookrightarrow \mathbb {C} ^{2}$ как указано $|w|^{2}+|z|^{2}=\varepsilon ^{2}.$ Функция $f$ имеет изолированную критическую точку $(0,0)\in \mathbb {C} ^{2}$ с $\partial f/\partial w=\partial f/\partial z=0$ тогда и только тогда, когда $w=z=0.$ Таким образом, мы рассматриваем структуру $V_{f}$ близко к $(0,0)\in \mathbb {C} ^{2}.$ Для этого рассмотрим пересечение $V_{f}\cap \mathbb {S} _{\varepsilon }^{3}\subset \mathbb {S} _{\varepsilon }^{3}.$ Это пересечение является так называемым звеном особенности. $f(w,z)=w^{p}+z^{q}.$ Ссылка на $f(w,z)=w^{p}+z^{q}$, где p и q взаимно просты и оба больше или равны двум, является в точности торическим узлом ( p , q ).

Список

(36,3) звено тора

Рисунок справа — звено тора (72,4).

• Развязать узел , 3 ₁ узел (3,2), 5 ₁ узел (5,2), 7 ₁ узел (7,2), 8 ₁₉ узел (4,3), 9 ₁ узел (9,2), 10 ₁₂₄ узла. (5,3)

Стол #	АБ	Изображение	П	вопрос	Крест #
0	0 1				0
3а1	3 1		2	3	3
5а2	5 1		2	5	5
7а7	7 1		2	7	7
8н3	8 19		3	4	8
9а41	9 1		2	9	9
10н21	10 124		3	5	10
11а367			2	11	11
13a4878			2	13	13
14н21881			3	7	14
15н41185		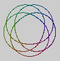	4	5	15
15а85263			2	15	15
16н783154			3	8	16
			2	17	17
			2	19	19
			3	10	20
			4	7	21
			2	21	21
			3	11	22
			2	23	23
			5	6	24
			2	25	25
			3	13	26
			4	9	27
			2	27	27
			5	7	28
			3	14	28
			2	29	29
			2	31	31
			5	8	32
			3	16	32
			4	11	33
			2	33	33
			3	17	34
			6	7	35
			2	35	35
			5	9	36
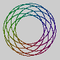			7	8	48
			7	9	54
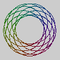			8	9	63

г -торический узел

Узел g-тора — это замкнутая кривая, нарисованная на g-торе . С технической точки зрения, это гомеоморфный образ круга в S³ , который можно реализовать как подмножество тела рода g -ручки в S³ (дополнением которого также является тело-ручка рода g ). Если ссылка является подмножеством тела ручки второго рода, это ссылка двойного тора .

Для второго рода простейшим примером двойного торического узла, который не является торовым узлом, является узел в форме восьмерки .

См. также

• Переменный узел
• Спутниковый узел
• Гиперболический узел
• Иррациональная обмотка тора
• Топополис

Внешние ссылки

• « 36 торических узлов », Атлас узлов .
• Вайсштейн, Эрик В. «Торовый узел» . Математический мир .
• Средство рендеринга тороидального узла в Actionscript
• Веселье с узлом PQ-Torus