Обратный узел
В математике , особенно в области топологии , известной как теория узлов , обратимый узел — это узел , который может непрерывно деформироваться сам по себе, но с обратной ориентацией. — Необратимый узел это любой узел, не обладающий этим свойством. Обратимость инвариант узла есть узла . Обратимая связь — это ссылка , эквивалентная обратимому узлу.
Существует только пять типов симметрии узлов, обозначаемых киральностью и обратимостью: полностью хиральный, обратимый, положительно амфихиральный необратимый, отрицательно амфихиральный необратимый и полностью амфихиральный обратимый. [1]
Фон
[ редактировать ]| Количество пересечений | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | OEIS Последовательность |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Необратимые узлы | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 33 | 187 | 1144 | 6919 | 38118 | 226581 | 1309875 | А052402 |
| Обратимые узлы | 1 | 1 | 2 | 3 | 7 | 20 | 47 | 132 | 365 | 1032 | 3069 | 8854 | 26712 | 78830 | А052403 |
Давно известно, что большинство простых узлов, таких как узел «трилистник» и узел «восьмерка», являются обратимыми. В 1962 году Ральф Фокс предположил, что некоторые узлы необратимы, но существование необратимых узлов не было доказано, пока Хейл Троттер не открыл в 1963 году бесконечное семейство необратимых узлов -кренделей. [2] Сейчас известно, что почти все узлы необратимы. [3]
Обратимые узлы
[ редактировать ]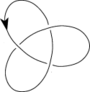
все узлы с числом пересечений Известно, что 7 и менее обратимы. Неизвестен общий метод, позволяющий определить, является ли данный узел обратимым. [4] Задачу можно перевести в алгебраические термины, [5] но, к сожалению, не существует известного алгоритма решения этой алгебраической задачи.
Если узел обратимый и амфихиральный , то он полностью амфихиральный. Самый простой узел с этим свойством — узел восьмерка. Хиральный узел, который является обратимым, классифицируется как обратимый узел. [6]
Сильно обратимые узлы
[ редактировать ]Более абстрактный способ определить обратимый узел — сказать, что существует сохраняющий ориентацию гомеоморфизм 3-сферы, который переводит узел в себя, но меняет ориентацию вдоль узла. Налагая более сильное условие, что гомеоморфизм также является инволюцией , т. е. имеет период 2 в группе гомеоморфизмов 3-сферы, мы приходим к определению сильно обратимого узла. Все узлы с туннелем номер один, такие как узел «трилистник» и узел «восьмерка» , строго обратимы. [7]
Необратимые узлы
[ редактировать ]
Простейшим примером необратимого узла является узел 8 17 (нотация Александра-Бриггса) или .2.2 ( нотация Конвея ). Узел -крендель 7, 5, 3 необратим, как и все узлы-крендели вида (2 p + 1), (2 q + 1), (2 r + 1), где p , q и r — различные целые числа, представляющие собой бесконечное семейство, необратимость которого доказал Троттер. [2]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Хосте, Джим; Тистлетвейт, Морвен; Уикс, Джефф (1998), «Первые 1 701 936 узлов» (PDF) , The Mathematical Intelligencer , 20 (4): 33–48, doi : 10.1007/BF03025227 , MR 1646740 , S2CID 18027155 , заархивировано из оригинала (PDF) на 15 декабря 2013 г.
- ^ Jump up to: Перейти обратно: а б Троттер, HF (1963), «Необратимые узлы существуют», Топология , 2 (4): 275–280, doi : 10.1016/0040-9383(63)90011-9 , MR 0158395 .
- ^ Мурасуги, Кунио (2007), Теория узлов и ее приложения , Springer, стр. 45, ISBN 9780817647186 .
- ^ Вайсштейн, Эрик В. «Обратный узел» . Математический мир . Доступ: 5 мая 2013 г.
- ^ Куперберг, Грег (1996), «Обнаружение обратимости узла», Журнал теории узлов и ее разветвлений , 5 (2): 173–181, arXiv : q-alg/9712048 , doi : 10.1142/S021821659600014X , MR 1395778 , S2CID 1529563 0 .
- ^ Кларк, В. Эдвин; Эльхамдади, Мохамед; Сайто, Масахико; Йитман, Тимоти (2013), «Квандловые раскраски узлов и приложений», Журнал теории узлов и ее разветвлений , 23 (6), arXiv : 1312.3307 , Bibcode : 2013arXiv1312.3307C , doi : 10.1142/S0218216514500357 , PMC 4610146 , ПМИД 26491208 .
- ^ Моримото, Кандзи (1995), «Есть узлы, число туннелей которых уменьшается при уменьшении связной суммы», Proceedings of the American Mathematical Society , 123 (11): 3527–3532, doi : 10.1090/S0002-9939-1995-1317043-4 , JSTOR 2161103 , MR 1317043 . См., в частности, лемму 5.
Внешние ссылки
[ редактировать ]- Джаблан, Славик и Сазданович, Радмила. Основная теория графов: необратимые узлы и связи. Архивировано 18 января 2011 г. на Wayback Machine , LinKnot .
- Пояснение с видео , Nrich.Maths.org .