Бруннская ссылка

В теории узлов , разделе топологии , брунновская связь — это нетривиальная ссылка , которая становится набором тривиальных несвязанных окружностей, если удалить какой-либо один компонент. Другими словами, вырезание любого цикла освобождает все остальные циклы (так что никакие два цикла не могут быть напрямую связаны ).
Название Брунниан происходит в честь Германа Брунна . Статья Брунна « О цепочке» 1892 года включала примеры таких связей.
Примеры [ править ]
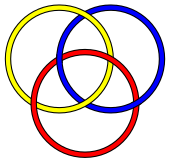

Самое известное и простое брунновское звено — это кольца Борромео , звено из трёх узлов . Однако для каждого числа три или выше существует бесконечное количество связей со свойством Брунна, содержащих это количество петель. Вот несколько относительно простых трехкомпонентных брунновских связей, которые не совпадают с кольцами Борромео:
- 12-переходное звено.
- 18-переходное звено.
- 24-переходное звено.
Простейшим брунновским звеном, отличным от 6-пересекающихся колец Борромео, предположительно является 10-пересекающееся звено L10a140 . [1]
Примером n- компонентной брунновской связи являются «резиновые» бруннианские связи, где каждый компонент зацикливается вокруг следующего как aba. −1 б −1 , причем последний обвивает первый, образуя круг. [2]
В 2020 году были обнаружены новые, гораздо более сложные брунновские связи. [3] используя очень гибкие методы геометрической топологии, гораздо больше, чем было построено ранее. См. раздел 6. [3]
Некруглость [ править ]
Брунновское звено невозможно построить из геометрических окружностей. В более общем плане, если связь обладает тем свойством, что каждый компонент представляет собой круг и никакие два компонента не связаны между собой, то это тривиально. Доказательство, проведенное Майклом Фридманом и Ричардом Скорой, включает трехмерное пространство, содержащее звено, в качестве границы шаровой модели Пуанкаре четырехмерного гиперболического пространства и рассматривает гиперболические выпуклые оболочки кругов. Это двумерные подпространства гиперболического пространства, и закономерности их пересечения отражают попарную связь окружностей: если две окружности связаны, то их оболочки имеют точку пересечения, но в предположении, что пары окружностей не связаны, корпуса не пересекаются. Если рассматривать сечения шара Пуанкаре концентрическими трехмерными сферами, то пересечение каждой сферы с оболочками кругов снова представляет собой звено, составленное из кругов, и это семейство сечений обеспечивает непрерывное движение всех круги, которые сжимают каждый из них до точки, не пересекая ни один из других. [4]
Классификация [ править ]
Брунновские связи были классифицированы Джоном Милнором с точностью до ( гомотопии связей Milnor 1954 ), а введенные им инварианты теперь называются инвариантами Милнора.
( n + 1)-компонентную брунновскую ссылку можно рассматривать как элемент группы ссылок – которая в этом случае (но не в общем случае) является фундаментальной группой – дополнения ссылки n - компонентной развязки, поскольку по Бруннианство: удаление последней ссылки отключает остальные. Группа связей n -компонентного unlink — это свободная группа на n генераторах, Fn , поскольку группа связей одиночной связи — это узлов unknot группа , которая представляет собой целые числа, а группа связей несвязанного союза — это бесплатный продукт из связующих групп компонентов.
Не каждый элемент группы связей дает брунновскую ссылку, поскольку удаление любого другого компонента также должно привести к отключению оставшихся n элементов. Милнор показал, что элементы группы, которые соответствуют брунновским связям, связаны с градуированной алгеброй Ли нижней центральной серии свободной группы, которую можно интерпретировать как «отношения» в свободной алгебре Ли .
В 2021 году были исследованы две специальные спутниковые операции для брунновских связей в 3-сфере, называемые «спутниковая сумма» и «спутниковая связь», обе из которых могут использоваться для создания бесконечного множества различных брунновских связей почти из каждой брунновской связи. [5] Дана теорема геометрической классификации брунновских зацеплений. [5] Что еще более интересно, была разработана каноническая геометрическая декомпозиция в терминах спутниковой суммы и спутниковой связи, которая проще, чем JSJ-разложение, для брунновских каналов. Строительными блоками брунновских связей в них оказываются -ссылки Хопфа, гиперболические брунновские связи и гиперболические брунновские связи в несвязных-дополнениях, последние из которых могут быть дополнительно сведены к брунновским связям в 3-сфере. [5]
Продукция Massey [ править ]
Брунновские связи можно понять в алгебраической топологии через произведения Мэсси : произведение Мэсси — это n -кратное произведение, которое определяется только в том случае, если все ( n - 1)-кратные произведения его членов исчезают. Это соответствует брунновскому свойству всех ( n - 1)-компонентных подссылок, которые не связаны, но общая n -компонентная ссылка связана нетривиально.
Брунниевские косы [ править ]

Брунновская коса — это коса, которая становится тривиальной при удалении любой из ее нитей. Брунновы косы образуют подгруппу группы кос . Брунновы косы над 2- сферой , не являющиеся брунновскими над 2- кругом, порождают нетривиальные элементы в гомотопических группах 2-сферы. Например, «стандартная» коса, соответствующая кольцам Борромео, порождает расслоение Хопфа S 3 → С 2 , и повторение этого (как при повседневном плетении) также является брунновским.
Реальные примеры [ править ]

Многие головоломки с распутыванием и некоторые механические головоломки представляют собой варианты Бруннианских связей, цель которых состоит в том, чтобы освободить одну часть, лишь частично связанную с остальными, тем самым демонтируя структуру.
Бруннианские цепи также используются для создания носимых и декоративных предметов из резинок с использованием таких устройств, как Rainbow Loom или Wonder Loom .
Ссылки [ править ]
- ^ Бар-Натан, Дрор (16 августа 2010 г.). « Может быть, все бруннианцы », [Академическое Омут памяти] .
- ^ "Резиновая лента" Брунниан Ссылки
- ^ Jump up to: Перейти обратно: а б Бай, Шэн; Ван, Вэйбяо (ноябрь 2020 г.). «Новые критерии и конструкции брунновских связей» . Журнал теории узлов и ее разветвлений . 29 (13): 2043008. arXiv : 2006.10290 . дои : 10.1142/S0218216520430087 . ISSN 0218-2165 .
- ^ Фридман, Майкл Х .; Скора, Ричард (1987), «Странные действия групп на сферах», Журнал дифференциальной геометрии , 25 : 75–98, doi : 10.4310/jdg/1214440725 ; см., в частности, лемму 3.2, с. 89
- ^ Jump up to: Перейти обратно: а б с Бай, Шэн; Ма, Цзимин (сентябрь 2021 г.). «Спутниковые конструкции и геометрическая классификация брунновских звеньев» . Журнал теории узлов и ее разветвлений . 30 (10): 2140005. arXiv : 1906.01253 . дои : 10.1142/S0218216521400058 . ISSN 0218-2165 .
Дальнейшее чтение [ править ]
- Беррик, А. Джон; Коэн, Фредерик Р.; Вонг, Ян Лой; Ву, Цзе (2006), «Конфигурации, косы и гомотопические группы» , Журнал Американского математического общества , 19 (2): 265–326, doi : 10.1090/S0894-0347-05-00507-2 , MR 2188127 .
- Герман Брунн, «О цепях», Й. Мюнх. Бер, XXII. 77–99 (1892). JFM 24.0507.01 (на немецком языке)
- Милнор, Джон (март 1954 г.), «Группы связей», Annals of Mathematics , 59 (2), Annals of Mathematics: 177–195, doi : 10.2307/1969685 , JSTOR 1969685
- Рольфсен, Дейл (1976), Узлы и связи , Серия лекций по математике, том. 7, Беркли, Калифорния : Опубликуй или погибни, ISBN 0-914098-16-0 , МР 0515288
Внешние ссылки [ править ]
- «Так ли редки борромеевские ссылки?», Славик Яблан (также доступен в исходной форме, опубликованной в журнале Forma здесь (PDF-файл) . Архивировано 28 февраля 2021 г. на Wayback Machine ).
- « Брунниан_линк », Атлас узлов .


