Ссылка на крендель

Узел кренделя (-2,3,7) имеет два правосторонних скручивания в первом клубке , три левых скручивания во втором и семь левых скручиваний в третьем.

P(5,3,-2) = T(5,3) = 10  ₁₂₄

Р(3,3,-2) = Т(4,3) = 8 ₁₉

Всего два узла — и тор, и крендель.

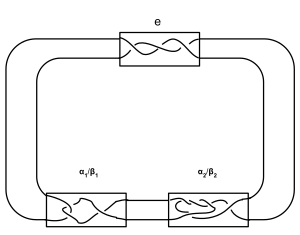
В математической теории узлов звено- крендель представляет собой особый вид звена . Он состоит из конечного числа клубков , состоящих из двух переплетающихся круговых спиралей . Клубки соединяются циклически, и первый компонент первого сплетения соединен со вторым компонентом второго сплетения, первый компонент второго сплетения соединен со вторым компонентом третьего сплетения и так далее. Наконец, первый компонент последнего клубка соединяется со вторым компонентом первого. Звено-крендель, которое также является узлом (то есть звеном с одним компонентом), является узлом-кренделем .

Каждый клубок характеризуется количеством витков: положительным, если они происходят против часовой стрелки или влево, отрицательными, если по часовой стрелке или вправо. В стандартной проекции $(p_{1},\,p_{2},\dots ,\,p_{n})$ ссылка на крендель, есть $p_{1}$левые переходы в первом клубке, $p_{2}$во втором и вообще $p_{n}$в н -ом.

Ссылку-крендель можно также описать как ссылку Монтесиноса с целочисленными клубками.

Некоторые основные результаты

The $(p_{1},p_{2},\dots ,p_{n})$ Ссылка на крендель является узлом, если и то, и другое $n$ и все $p_{i}$ являются нечетными или в точности одними из $p_{i}$ четный.

The $(p_{1},\,p_{2},\dots ,\,p_{n})$ Ссылка на крендель разделяется, если хотя бы два из $p_{i}$ равны нулю ; но обратное неверно.

The $(-p_{1},-p_{2},\dots ,-p_{n})$ ссылка на крендель является зеркальным отражением ссылки $(p_{1},\,p_{2},\dots ,\,p_{n})$ ссылка на крендель.

The $(p_{1},\,p_{2},\dots ,\,p_{n})$ связь кренделя изотопна $(p_{2},\,p_{3},\dots ,\,p_{n},\,p_{1})$ ссылка на крендель. Таким образом, тоже $(p_{1},\,p_{2},\dots ,\,p_{n})$ связь кренделя изотопна $(p_{k},\,p_{k+1},\dots ,\,p_{n},\,p_{1},\,p_{2},\dots ,\,p_{k-1})$ ссылка на крендель.

The $(p_{1},\,p_{2},\,\dots ,\,p_{n})$ связь кренделя изотопна $(p_{n},\,p_{n-1},\dots ,\,p_{2},\,p_{1})$ ссылка на крендель. Однако если ориентировать ссылки каноническим образом, то эти две ссылки будут иметь противоположные ориентации.

Некоторые примеры

Узел кренделя (1, 1, 1) — это (правосторонний) трилистник ; узел кренделя (−1, −1, −1) является его зеркальным отражением .

Узел-крендель (5, −1, −1) — это стивидорный узел (6 ₁ ).

Если p , q , r — различные нечетные целые числа, большие 1, то узел-крендель ( p , q , r ) является необратимым узлом .

Звено-крендель (2 p , 2 q , 2 r ) представляет собой звено, образованное тремя связанными узлами .

Узел-крендель (−3, 0, −3) ( квадратный узел (математика) ) — это связная сумма двух узлов-трилистника .

Звено-крендель (0, q 0) представляет собой расщепленное объединение узла , и другого узла.

Монтесинос

Ссылка Montesinos — это особый вид ссылки , которая обобщает ссылки-крендельки (ссылку-крендель также можно описать как ссылку Montesinos с целочисленными связками). Ссылка Монтесиноса, которая также является узлом (т. е. связь с одним компонентом), является узлом Монтесиноса .

Связь Монтесиноса состоит из нескольких рациональных клубков . Одно из обозначений ссылки Монтесинос: $K(e;\alpha _{1}/\beta _{1},\alpha _{2}/\beta _{2},\ldots ,\alpha _{n}/\beta _{n})$.

В этих обозначениях $e$ и все $\alpha _{i}$ и $\beta _{i}$ являются целыми числами. Ссылка Монтесиноса, заданная этим обозначением, состоит из суммы рациональных клубков, заданных целым числом $e$ и рациональные путаницы $\alpha _{1}/\beta _{1},\alpha _{2}/\beta _{2},\ldots ,\alpha _{n}/\beta _{n}$

Эти узлы и связи названы в честь испанского тополога Хосе Марии Монтесиноса Амилибиа , который впервые представил их в 1973 году.

Утилита

(−2, 3, 2 n + 1) кренделя особенно полезны при изучении 3-многообразий . Было получено множество результатов о многообразиях, возникающих в результате хирургии Дена, в частности, на узле кренделя (−2,3,7) .

Гиперболический объем дополнения звена кренделя (-2,3,8) превышает в 4 раза константу Каталана , примерно 3,66. Это дополнение к звену кренделя является одним из двух двускапных гиперболических многообразий с минимально возможным объемом, другое — дополнением звена Уайтхеда .

Ссылка на Монтесинос. В этом примере $e=-3$ , $\alpha _{1}/\beta _{1}=-3/2$ и $\alpha _{2}/\beta _{2}=5/2$.

Съедобный (−2,3,7) узел-крендель

Еще один съедобный (–2,3,7) узелок кренделя, идеально глазированный.

Дальнейшее чтение

• Троттер, Хейл Ф.: Необратимые узлы существуют , Топология , 2 (1963), 272–280.
• Бурде, Герхард; Цишанг, Хайнер (2003). Узлы . Де Грюйтер изучает математику. Том 5 (2-е исправленное и расширенное изд.). Вальтер де Грюйтер. ISBN  3110170051 . ISSN   0179-0986 . Збл   1009.57003 .