Бесплатная группа

В математике свободная группа FS _аксиом над данным множеством S состоит из всех слов , которые могут быть построены из членов S , считая два слова разными, если только их равенство не следует из группы (например, st = suu ⁻¹т, но с ≠ т ⁻¹ для s , т , ты ∈ S ). Члены S называются генераторами FS , а _ранг количество образующих — это свободной группы.Произвольная группа G называется свободной если она изоморфна FS , _{можно записать ровно одним способом в виде} для некоторого подмножества S группы G , т. е. если существует подмножество S группы G такое, что каждый элемент группы G произведения конечного числа многие элементы S и их обратные (несмотря на тривиальные варианты, такие как st = suu ⁻¹т ).

Родственное, но отличное понятие — это свободная абелева группа ; оба понятия являются частными случаями свободного объекта универсальной алгебры . По сути, свободные группы определяются своим универсальным свойством .

История [ править ]

Свободные группы впервые возникли при изучении гиперболической геометрии , как примеры фуксовых групп (дискретных групп, действующих изометриями на гиперболической плоскости ). В статье 1882 года Вальтер фон Дейк отметил, что эти группы имеют простейшие возможные представления . ^[1] Алгебраическое изучение свободных групп было начато Якобом Нильсеном в 1924 году, который дал им название и установил многие их основные свойства. ^[2]^[3]^[4] Макс Ден осознал связь с топологией и получил первое доказательство полной теоремы Нильсена-Шрайера . ^[5] Отто Шрайер опубликовал алгебраическое доказательство этого результата в 1927 году. ^[6] а Курт Райдемейстер включил всестороннее рассмотрение свободных групп в свою книгу 1932 года по комбинаторной топологии . ^[7] Позже, в 1930-х годах, Вильгельм Магнус обнаружил связь между нижним центральным рядом свободных групп и свободными алгебрами Ли .

Примеры [ править ]

Группа ( Z ,+) целых чисел свободна от ранга 1; генераторный набор — S = {1}. Целые числа также являются свободной абелевой группой , хотя все свободные группы ранга $\geq 2$ неабелевы. Свободная группа на двухэлементном множестве S встречается при доказательстве парадокса Банаха–Тарского и там описана.

С другой стороны, любая нетривиальная конечная группа не может быть свободной, поскольку элементы свободного порождающего множества свободной группы имеют бесконечный порядок.

В алгебраической топологии фундаментальная группа букета из k кругов (набора из k петель, имеющих только одну общую точку) является свободной группой на множестве из k элементов.

Строительство [ править ]

Свободную группу F _S со свободным порождающим множеством S можно построить следующим образом. S — набор символов, и мы предполагаем, что для каждого s в S существует соответствующий «обратный» символ s . ⁻¹, в наборе S ⁻¹. Пусть T = S ∪ S ⁻¹и определим слово в S как любое письменное произведение элементов T . То есть слово в S является элементом моноида , порожденного T . Пустое слово — это слово вообще без символов. Например, если S = { a , b , c }, то T = { a , a ⁻¹, б , б ⁻¹, с , с ⁻¹}, и

ab^{3}c^{-1}ca^{-1}c\,

это слово на S. языке

Если элемент S находится непосредственно рядом с обратным, слово можно упростить, опустив символы c, c. ⁻¹ пара:

ab^{3}c^{-1}ca^{-1}c\;\;\longrightarrow \;\;ab^{3}\,a^{-1}c.

Слово, которое нельзя упростить дальше, называется сокращенным .

Свободная группа FS _. определяется как группа всех сокращенных слов в S с конкатенацией слов (с последующей редукцией, если необходимо) в качестве групповой операции Личность – это пустое слово.

Сокращенное слово называется циклически сокращенным , если его первая и последняя буквы не обратны друг другу. Каждое слово сопряжено с циклически сокращенным словом, а циклически сокращенное сопряжение циклически сокращенного слова представляет собой циклическую перестановку букв в слове. например б ⁻¹abcb не циклически сокращается, а сопряжен с abc , который циклически сокращается. Единственными циклически восстанавливаемыми конъюгатами abc являются abc , bca и cab .

Универсальная собственность [ править ]

Свободная группа FS _{группа ,} это универсальная порожденная множеством S. — можно формализовать следующим универсальным свойством : для любой функции $f$ из S в группу G существует единственный φ : FS → _Это G , делающий коммутируемой следующую диаграмму (где безымянное отображение обозначает включение из S в FS _{гомоморфизм} ):

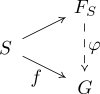
То есть гомоморфизмы F _S → G находятся во взаимно однозначном соответствии с функциями S → G . Для несвободной группы наличие отношений ограничивало бы возможные образы образующих при гомоморфизме.

Чтобы увидеть, как это связано с конструктивным определением, представьте себе отображение S в FS _. как отправку каждого символа в слово, состоящее из этого символа Чтобы построить φ для заданного $f$ , сначала обратите внимание, что отправляет пустое слово в единицу G и оно должно согласовываться с $f$ по элементам S. φ Для остальных слов (состоящих из более чем одного символа) φ можно расширить однозначно, поскольку это гомоморфизм, т. е. φ ( ab ) = φ ( a ) φ ( b ).

Вышеупомянутое свойство характеризует свободные группы с точностью до изоморфизма и иногда используется как альтернативное определение. Это известно как свойство свободных групп, а порождающий набор S называется базисом для FS _{универсальное} . Базис свободной группы не определен однозначно.

Характеризоваться универсальным свойством — стандартная особенность свободных объектов в универсальной алгебре . На языке теории категорий конструкция свободной группы (аналогично большинству конструкций свободных объектов) представляет собой функтор из категории множеств в категорию групп . Этот функтор остается сопряженным с функтором забывчивости от групп к множествам.

Факты и теоремы [ править ]

Некоторые свойства свободных групп легко следуют из определения:

Любая группа G является гомоморфным образом некоторой свободной группы F _S . Пусть S множество образующих группы G. — Естественное отображение φ : FS _{, что и} → G является эпиморфизмом доказывает утверждение. Эквивалентно, G изоморфна факторгруппе некоторой свободной FS _. группы Если здесь S можно выбрать конечным, то G называется конечно порожденным . Ядро Ker( φ) совокупность всех отношений представления это G — ; если Ker( φ) может быть порожден сопряжениями конечного числа элементов F , то G конечно представима.
Если S имеет более одного элемента, то тривиален _. ( то есть состоит только ) _{FS не абелева, и фактически центр FS} из единичного элемента
Две свободные группы FS _когда и FT _S изоморфны тогда и только тогда, и T имеют одинаковую мощность . Эта мощность называется рангом свободной группы F . Таким образом, для каждого кардинального числа k существует с точностью до изоморфизма ровно одна свободная группа ранга k .
Свободная группа конечного ранга n > 1 имеет экспоненциальную скорость роста порядка 2 n − 1.

Несколько других связанных результатов:

Теорема Нильсена -Шрайера : каждая подгруппа свободной группы свободна. Более того, если свободная группа F имеет ранг n , а подгруппа H имеет индекс e в F , то H свободна ранга 1 + e ( n – 1).
Свободная группа ранга k, очевидно, имеет подгруппы любого ранга меньше k . Менее очевидно, что ( неабелева! ) свободная группа ранга не ниже 2 имеет подгруппы всех счетных рангов.
Коммутант k свободной группы ранга > 1 имеет бесконечный ранг; например, для F( a , b ) он свободно генерируется коммутаторами [ a ^м, б ^н] для ненулевых m и n .
Свободная группа из двух элементов является SQ универсальной ; сказанное выше следует из того, что любая универсальная группа SQ имеет подгруппы всех счетных рангов.
Любая группа, действующая на дереве свободно и сохраняющая ориентацию свободной группой счетного ранга (задаваемого единицей плюс характеристика факторграфа , является эйлерова ).
Граф Кэли свободной группы конечного ранга относительно свободного порождающего множества — это дерево , на котором группа действует свободно, сохраняя ориентацию. Как топологическое пространство (одномерный симплициальный комплекс ), этот граф Кэли Γ( F ) стягиваем . Для конечно представленной группы G естественный гомоморфизм, определенный выше, φ : F → G , определяет отображение покрытия графов Кэли φ* : Γ( F ) → Γ( G ), фактически универсальное накрытие. Следовательно, фундаментальная группа графа Кэли Γ( G ) изоморфна ядру φ подгруппе отношений среди образующих G. , нормальной Крайний случай - это когда G = { e }, тривиальная группа, рассматриваемая с таким же количеством образующих, как F , и все они тривиальны; граф Кэли Γ( G ) представляет собой букет окружностей, а его фундаментальная группа — это F. сама
Любая подгруппа свободной группы, $H\subset F$ , соответствует накрывающему пространству букета кругов, а именно смежных классов Шрайера графу F / H . Это можно использовать для топологического доказательства приведенной выше теоремы Нильсена-Шрайера.
Группоидный подход к этим результатам, представленный в работе П. Дж . Хиггинса ниже, связан с использованием вышеприведенных накрывающих пространств . Это позволяет получить более мощные результаты, например, по теореме Грушко и нормальную форму фундаментального группоида графа групп. В этом подходе широко используются свободные группоиды на ориентированном графе.
Из теоремы Грушко следует, что если подмножество B свободной группы F на n элементах порождает F и имеет n элементов, то B порождает F. свободно

Свободная абелева группа [ править ]

Свободная абелева группа на множестве S определяется через ее универсальность аналогичным образом с очевидными изменениями:Рассмотрим пару ( F , φ ), где F — абелева группа, а φ : S → F — функция. F называется свободной абелевой группой на S относительно φ, если для любой абелевой группы G и любой функции ψ : S → G существует единственный гомоморфизм f : F → G такой, что

ж ( φ ( s )) знак равно ψ ( s ), для всех s в S .

Свободную абелеву группу на S можно явно идентифицировать как свободную группу F( S ) по модулю подгруппы, порожденной ее коммутаторами, [F( S ), F( S )], т.е.его абелианизация . Другими словами, свободная абелева группа на S — это набор слов, различающихся только до порядка букв. Поэтому ранг свободной группы можно также определить как ранг ее абелианизации как свободной абелевой группы.

Проблемы Тарского [ править ]

Примерно в 1945 году Альфред Тарский задался вопросом, имеют ли свободные группы с двумя или более образующими одну и ту же теорию первого порядка и разрешима ли эта теория . Села (2006) ответил на первый вопрос, показав, что любые две неабелевы свободные группы имеют одну и ту же теорию первого порядка, а Харлампович и Мясников (2006) ответили на оба вопроса, показав, что эта теория разрешима.

Аналогичный нерешенный (по состоянию на 2011 год) вопрос в свободной теории вероятностей спрашивает, изоморфны ли групповые алгебры фон Неймана любых двух неабелевых конечно порожденных свободных групп.

См. также [ править ]

Примечания [ править ]

^ Дейк, Вальтер (1882). «Теоретико-групповые исследования» . Математические летописи . 20 (1): 1–44. дои : 10.1007/BF01443322 . S2CID 179178038 . Архивировано из оригинала 4 марта 2016 г. Проверено 1 сентября 2015 г.
^ Нильсен, Джейкоб (1917). «Изоморфизмы общей бесконечной группы с двумя образующими» . Математические летописи . 78 (1): 385–397. дои : 10.1007/BF01457113 . ЖФМ 46.0175.01 . МР1511907 . S2CID 119726936 . Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.
^ Нильсен, Якоб (1921). «О расчетах с некоммутативными коэффициентами и их применении в теории групп. (Перевод с датского)». Ученый-математик . 6 (1981) (2): 73–85.
^ Нильсен, Джейкоб (1924). «Группа изоморфизмов свободных групп» . Математические летописи . 91 (3): 169–209. дои : 10.1007/BF01556078 . S2CID 122577302 . Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.
^ См. Магнус, Вильгельм ; Муфанг, Рут (1954). «Макс Ден на память» . Математические летописи . 127 (1): 215–227. дои : 10.1007/BF01361121 . S2CID 119917209 . Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.
^ Шрайер, Отто (1928). «Подгруппы свободных групп». Трактаты математического семинара Гамбургского университета . 5 : 161-183. дои : 10.1007/BF02952517 . S2CID 121888949 .
^ Рейдемейстер, Курт (1972) [1932]. Введение в комбинаторную топологию . Дармштадт: Научное книжное общество.

Ссылки [ править ]

Харлампович, Ольга; Мясников, Алексей (2006). «Элементарная теория свободных неабелевых групп» . Журнал алгебры . 302 (2): 451–552. дои : 10.1016/j.jalgebra.2006.03.033 . МР 2293770 .
В. Магнус, А. Каррасс и Д. Солитар, «Комбинаторная теория групп», Дувр (1976).
П. Дж. Хиггинс, 1971, «Категории и группоиды», ван Ностранд, {Нью-Йорк}. Перепечатки по теории и приложениям категорий, 7 (2005), стр. 1–195.
Села, Злил (2006). «Диофантова геометрия над группами. VI. Элементарная теория свободной группы». Геом. Функц. Анал . 16 (3): 707–730. дои : 10.1007/s00039-006-0565-8 . МР 2238945 . S2CID 123197664 .
Серр, Жан-Пьер , Деревья , Спрингер (2003) (английский перевод «arbres, amalgams, SL ₂ », 3-е издание, звездочка 46 (1983))
П. Дж. Хиггинс, Фундаментальный группоид графа групп , Журнал Лондонского математического общества (2) 13 (1976), вып. 1, 145–149.
Алуффи, Паоло (2009). Алгебра: Глава 0 . Книжный магазин АМС. п. 70. ИСБН 978-0-8218-4781-7 . .
Грилье, Пьер Антуан (2007). Абстрактная алгебра . Спрингер. п. 27. ISBN 978-0-387-71567-4 . .

[1] Дейк, Вальтер (1882). «Теоретико-групповые исследования» . Математические летописи . 20 (1): 1–44. дои : 10.1007/BF01443322 . S2CID 179178038 . Архивировано из оригинала 4 марта 2016 г. Проверено 1 сентября 2015 г.

[2] Нильсен, Джейкоб (1917). «Изоморфизмы общей бесконечной группы с двумя образующими» . Математические летописи . 78 (1): 385–397. дои : 10.1007/BF01457113 . ЖФМ 46.0175.01 . МР1511907 . S2CID 119726936 . Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.

[3] Нильсен, Якоб (1921). «О расчетах с некоммутативными коэффициентами и их применении в теории групп. (Перевод с датского)». Ученый-математик . 6 (1981) (2): 73–85.

[4] Нильсен, Джейкоб (1924). «Группа изоморфизмов свободных групп» . Математические летописи . 91 (3): 169–209. дои : 10.1007/BF01556078 . S2CID 122577302 . Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.

[5] См. Магнус, Вильгельм ; Муфанг, Рут (1954). «Макс Ден на память» . Математические летописи . 127 (1): 215–227. дои : 10.1007/BF01361121 . S2CID 119917209 . Архивировано из оригинала 05 марта 2016 г. Проверено 1 сентября 2015 г.

[6] Шрайер, Отто (1928). «Подгруппы свободных групп». Трактаты математического семинара Гамбургского университета . 5 : 161-183. дои : 10.1007/BF02952517 . S2CID 121888949 .

[7] Рейдемейстер, Курт (1972) [1932]. Введение в комбинаторную топологию . Дармштадт: Научное книжное общество.

[1]

[2]

[3]

[4]

[5]

[6]

[7]