Гипотеза Римана

Чтобы узнать о музыкальном термине, см. риманову теорию .

Этот график дзета ( ζ ) функции Римана (здесь с аргументом z) показывает тривиальные нули, где ζ ( z ) = 0, полюс, где ζ ( z ) = $\infty$, критическая линия нетривиальных нулей с Re( z ) = 1/2 и наклонами абсолютных значений.

В математике гипотеза Римана — это гипотеза о том, что дзета-функция Римана имеет нули только в отрицательных четных целых числах и комплексных числах с действительной частью. 1/2 ​ ​ . Многие считают это важнейшей нерешенной проблемой чистой математики . Это представляет большой интерес для теории чисел , поскольку предполагает результаты о распределении простых чисел . Его предложил Бернхард Риман ( 1859 ), в честь которого он и назван.

Гипотеза Римана и некоторые ее обобщения, наряду с гипотезой Гольдбаха и гипотезой о простых числах-близнецах , составляют восьмую проблему Гильберта в Дэвида Гильберта списке двадцати трех нерешенных проблем ; это также одна из математики Клэя Института задач, удостоенных Премии тысячелетия , которая предлагает 1 миллион долларов США любому, кто решит любую из них. Это название также используется для некоторых тесно связанных аналогов, таких как гипотеза Римана для кривых над конечными полями .

Дзета-функция Римана ζ ( s ) — это функция которой , аргументом s может быть любое комплексное число, кроме 1, и чьи значения также являются комплексными. Он имеет нули в отрицательных четных целых числах; то есть ζ ( s ) = 0, когда s является одним из −2, −4, −6, .... Они называются его тривиальными нулями . Дзета-функция также равна нулю для других значений s , которые называются нетривиальными нулями . Гипотеза Римана касается расположения этих нетривиальных нулей и утверждает, что:

Действительная часть каждого нетривиального нуля дзета-функции Римана равна 1 / 2 .

Таким образом, если гипотеза верна, все нетривиальные нули лежат на критической прямой, состоящей из комплексных чисел 1/2 , а + i t , где t — действительное число — i единица мнимая .

Дзета-функция Римана

Дзета -функция Римана определяется для комплексных s с действительной частью больше 1 абсолютно сходящимся бесконечным рядом

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots$

Леонард Эйлер уже рассматривал этот ряд в 1730-х годах для реальных значений s в сочетании с его решением Базельской проблемы . Он также доказал, что оно равно произведению Эйлера.

$\zeta (s)=\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}={\frac {1}{1-2^{-s}}}\cdot {\frac {1}{1-3^{-s}}}\cdot {\frac {1}{1-5^{-s}}}\cdot {\frac {1}{1-7^{-s}}}\cdots$

где бесконечное произведение распространяется на все простые числа p .

Гипотеза Римана обсуждает нули вне области сходимости этого ряда и произведения Эйлера. Чтобы разобраться в гипотезе, необходимо аналитически продолжить функцию, чтобы получить форму, справедливую для всех комплексных s . Поскольку дзета-функция мероморфна , любой выбор того, как выполнить это аналитическое продолжение, приведет к одному и тому же результату по теореме тождества . Первый шаг в этом продолжении заключается в том, что ряды для дзета-функции и эта-функции Дирихле удовлетворяют соотношению

$\left(1-{\frac {2}{2^{s}}}\right)\zeta (s)=\eta (s)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}={\frac {1}{1^{s}}}-{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}-\cdots ,$

в области сходимости для обоих рядов. Однако ряд дзета-функций справа сходится не только тогда, когда действительная часть s больше единицы, но и в более общем смысле всякий раз, когда s имеет положительную действительную часть. Таким образом, дзета-функция может быть переопределена как $\eta (s)/(1-2/2^{s})$, расширяя его от Re( s ) > 1 до большей области: Re( s ) > 0 , за исключением точек, где $1-2/2^{s}$ равен нулю. Это точки $s=1+2\pi in/\log 2$ где $n$ может быть любым ненулевым целым числом; дзета-функция также может быть расширена до этих значений, взяв пределы (см. Эта-функция Дирихле § Задача Ландау с ζ ( s ) = η ( s )/0 и решения ), давая конечное значение для всех значений s с положительной действительной частью за исключением простого полюса при s = 1.

В полосе 0 < Re( s ) < 1 это расширение дзета-функции удовлетворяет функциональному уравнению

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s).$

Затем можно определить ζ ( s ) для всех оставшихся ненулевых комплексных чисел s ( Re( s ) ≤ 0 и s ≠ 0), применив это уравнение вне полосы и полагая ζ ( s ) равным правой части уравнения всякий раз, когда s имеет неположительную действительную часть (и s ≠ 0).

Если s — отрицательное четное целое число, то ζ ( s ) = 0, поскольку множитель sin( π s /2) равен нулю; это тривиальные нули дзета-функции. (Если s — положительное четное целое число, этот аргумент не применяется, поскольку нули синусоидальной функции сокращаются полюсами гамма -функции , поскольку она принимает отрицательные целые аргументы.)

Значение ζ (0) = −1/2 не определяется функциональным уравнением, а является предельным значением ζ ( s ) при стремлении s к нулю. Функциональное уравнение также подразумевает, что дзета-функция не имеет нулей с отрицательной действительной частью, кроме тривиальных нулей, поэтому все нетривиальные нули лежат в критической полосе , где s имеет действительную часть от 0 до 1.

• 
  Дзета-функция Римана вдоль критической линии с Re( s ) = 1/2. Реальные значения показаны на горизонтальной оси, а мнимые значения — на вертикальной оси. Re( ζ (1/2 + it )), Im( ζ (1/2 + it )) отображается на графике с t в диапазоне от -30 до 30.
• Продолжительность: 23 секунды. 0:23
  Анимация, показывающая в 3D критическую полосу дзета-функции Римана (синяя, где s имеет действительную часть от 0 до 1), критическую линию (красная, действительная часть s равна 0,5) и нули (пересечение красного и оранжевого): [ x , y , z ] = [Re( ζ ( r + it )), Im ( ζ ( r + it )), t ] с 0,1 ≤ r ≤ 0,9 и 1 ≤ t ≤ 51
• 
  Действительная часть (красный) и мнимая часть (синий) дзета-функции Римана ζ ( s ) вдоль критической линии в комплексной плоскости с вещественной частью Re( s ) = 1/2. Первые нетривиальные нули, где ζ( s ) равно нулю, возникают там, где обе кривые касаются горизонтальной оси x, для комплексных чисел с мнимыми частями Im( s ), равными ±14,135, ±21,022 и ±25,011.

Происхождение

...весьма вероятно, что все корни настоящие. Конечно, было бы желательно строгое доказательство этого; Однако после нескольких мимолетных безуспешных попыток я пока отложил его поиски в сторону, так как они показались мне ненужными для следующей цели моего расследования.

... весьма вероятно, что все корни настоящие. Конечно, здесь хотелось бы строгого доказательства; На данный момент, после нескольких мимолетных тщетных попыток, я временно отложил поиски этого вопроса, так как он кажется ненужным для непосредственной цели моего исследования.

- Изложение Риманом гипотезы Римана из ( Riemann 1859 ). (Он обсуждал версию дзета-функции, модифицированную таким образом, чтобы ее корни (нули) были действительными, а не лежали на критической прямой.)

После смерти Римана среди его бумаг была найдена заметка, в которой говорилось: «Эти свойства ζ ( s ) (рассматриваемой функции) выводятся из ее выражения, которое, однако, мне не удалось достаточно упростить, чтобы опубликовать его». ."Мы до сих пор не имеем ни малейшего представления о том, что это могло бы быть за выражение. Что касается свойств, которые он просто провозгласил, то прошло около тридцати лет, прежде чем я смог доказать их все, кроме одного (сама гипотеза Римана).

- Жак Адамар , Разум математика, VIII. Парадоксальные случаи интуиции

Первоначальной мотивацией Римана к изучению дзета-функции и ее нулей было их появление в его явной формуле для количества простых чисел π ( x ), меньших или равных заданному числу x , которую он опубликовал в своей статье 1859 года « О числе простых чисел ». Меньше заданной величины ». Его формула была дана через родственную функцию

$\Pi (x)=\pi (x)+{\tfrac {1}{2}}\pi (x^{1/2})+{\tfrac {1}{3}}\pi (x^{1/3})+{\tfrac {1}{4}}\pi (x^{1/4})+{\tfrac {1}{5}}\pi (x^{1/5})+{\tfrac {1}{6}}\pi (x^{1/6})+\cdots$

который подсчитывает простые числа и степени простых чисел до x , считая степень простых чисел p ^н как 1 ⁄ п . Количество простых чисел можно восстановить из этой функции с помощью формулы обращения Мёбиуса :

${\begin{aligned}\pi (x)&=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi (x^{1/n})\\&=\Pi (x)-{\frac {1}{2}}\Pi (x^{1/2})-{\frac {1}{3}}\Pi (x^{1/3})-{\frac {1}{5}}\Pi (x^{1/5})+{\frac {1}{6}}\Pi (x^{1/6})-\cdots ,\end{aligned}}$

где ц — функция Мёбиуса . Тогда формула Римана будет

$\Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\log 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\log t}}$

где сумма ведется по нетривиальным нулям дзета-функции и где Π ₀ — слегка модифицированная версия Π, которая заменяет свое значение в точках разрыва средним значением ее верхнего и нижнего пределов:

$\Pi _{0}(x)=\lim _{\varepsilon \to 0}{\frac {\Pi (x-\varepsilon )+\Pi (x+\varepsilon )}{2}}.$

Суммирование в формуле Римана не является абсолютно сходящимся, но его можно оценить, расположив нули ρ в порядке абсолютного значения их мнимой части. Функция li, входящая в первый член, представляет собой (несмещенную) логарифмическую интегральную функцию, определяемую главным значением Коши расходящегося интеграла

$\operatorname {li} (x)=\int _{0}^{x}{\frac {dt}{\log t}}.$

Члены li( x ^р ), включающие нули дзета-функции, требуют некоторой осторожности при их определении, поскольку li имеет точки ветвления в точках 0 и 1 и определяется (при x > 1) аналитическим продолжением по комплексной переменной ρ в области Re( ρ ) > 0. , т.е. их следует рассматривать как Ei ( ρ log x ) . Остальные члены также соответствуют нулям: доминирующий член li( x ) исходит из полюса в точке s = 1, рассматриваемого как ноль кратности −1, а остальные малые члены происходят из тривиальных нулей. Некоторые графики сумм первых нескольких членов этого ряда см. в Riesel & Göhl (1970) или Zagier (1977) .

Эта формула говорит, что нули дзета-функции Римана управляют колебаниями простых чисел вокруг их «ожидаемых» положений. Риман знал, что нетривиальные нули дзета-функции симметрично распределены относительно прямой s = 1/2 + it , и он знал, что все ее нетривиальные нули должны лежать в диапазоне 0 ≤ Re( s ) ≤ 1. Он проверил, что несколько нулей лежат на критической линии с действительной частью 1/2, и предложил так сделать всем; это гипотеза Римана.

Этот результат привлек воображение большинства математиков, потому что он настолько неожиданный, соединяющий две, казалось бы, несвязанные области математики; а именно, теория чисел , которая изучает дискретное, и комплексный анализ , который занимается непрерывными процессами. ( Бертон 2006 , стр. 376)

Последствия

Практическое использование гипотезы Римана включает в себя множество утверждений, которые, как известно, верны в соответствии с гипотезой Римана, а также некоторые из них, которые, как можно показать, эквивалентны гипотезе Римана.

Распределение простых чисел

Явная формула Римана для количества простых чисел, меньших заданного числа, гласит, что в терминах суммы по нулям дзета-функции Римана величина колебаний простых чисел вокруг их ожидаемого положения контролируется действительными частями нулей. дзета-функции. В частности, член ошибки в теореме о простых числах тесно связан с положением нулей. Например, если β — верхняя граница действительных частей нулей, то $\pi (x)-\operatorname {li} (x)=O\left(x^{\beta }\log x\right)$, где $\pi (x)$ — функция подсчета простых чисел , $\operatorname {li} (x)$ – логарифмическая интегральная функция , $\log(x)$ — натуральный логарифм x . , обозначение «большое О» здесь используется Уже известно, что 1/2 ≤ β ≤ 1.

Поправки к оценке функции подсчета простых чисел с использованием нулей дзета-функции. Величина поправочного члена определяется реальной частью нуля, добавляемого в поправку.

Фон Кох (1901) доказал, что гипотеза Римана предполагает «наилучшую возможную» оценку ошибки теоремы о простых числах. Точная версия результата Коха, полученная Шенфельдом (1976) , гласит, что гипотеза Римана подразумевает

$|\pi (x)-\operatorname {li} (x)|<{\frac {1}{8\pi }}{\sqrt {x}}\log(x),\qquad {\text{for all }}x\geq 2657,$

Шенфельд (1976) также показал, что гипотеза Римана подразумевает

$|\psi (x)-x|<{\frac {1}{8\pi }}{\sqrt {x}}\log ^{2}x,\qquad {\text{for all }}x\geq 73.2,$

где $\psi (x)$ — вторая функция Чебышева .

Дудек (2014) доказал, что из гипотезы Римана следует, что для всех $x\geq 2$ есть простое число $p$ удовлетворяющий

$x-{\frac {4}{\pi }}{\sqrt {x}}\log x<p\leq x$.

Константа 4/ π можетможно свести к (1 + ε ) при условии, что x выбрано достаточно большим. Это явный вариант теоремы Крамера .

Рост арифметических функций

Гипотеза Римана предполагает строгие ограничения на рост многих других арифметических функций , в дополнение к функции подсчета простых чисел, указанной выше.

Одним из примеров является функция Мёбиуса μ. Утверждение о том, что уравнение

${\frac {1}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}$

справедливо для любого s с действительной частью больше 1/2, при этом сумма в правой части сходится, что эквивалентно гипотезе Римана. Отсюда мы также можем заключить, что если функция Мертенса определяется формулой

$M(x)=\sum _{n\leq x}\mu (n)$

тогда утверждение, что

$M(x)=O\left(x^{{\frac {1}{2}}+\varepsilon }\right)$

для каждого положительного ε эквивалентно гипотезе Римана ( JE Littlewood , 1912; см., например: параграф 14.25 в Titchmarsh (1986) ). Определитель равен M порядка n матрицы Редхеффера ( n ) , поэтому гипотезу Римана также можно сформулировать как условие роста этих определителей. С тех пор результат Литтлвуда несколько раз улучшал Эдмунд Ландау . Эдвард Чарльз Титчмарш , Хельмут Майер и Хью Монтгомери и Каннан Саундарараджан . Результат Саундарараджана состоит в том, что при условии соблюдения гипотезы Римана

$M(x)=O\left(x^{1/2}\exp \left((\log x)^{1/2}(\log \log x)^{14}\right)\right).$

Гипотеза Римана накладывает довольно жесткие ограничения на рост M , поскольку Одлизко и те Риле (1985) опровергли несколько более сильную гипотезу Мертенса.

$|M(x)|\leq {\sqrt {x}}.$

Другой тесно связанный результат принадлежит Бьёрнеру (2011) о том, что гипотеза Римана эквивалентна утверждению, что эйлерова характеристика , симплициального комплекса определяемого решеткой целых чисел при делимости, равна $o(n^{1/2+\epsilon })$ для всех $\epsilon >0$ (см. алгебру инцидентности ).

Гипотеза Римана эквивалентна многим другим гипотезам о скорости роста других арифметических функций, кроме µ( n ). Типичным примером является теорема Робина , в котором говорится, что если σ( n ) является сигма-функцией , заданной формулой

$\sigma (n)=\sum _{d\mid n}d$

затем

$\sigma (n)<e^{\gamma }n\log \log n$

для всех n > 5040 тогда и только тогда, когда верна гипотеза Римана, где γ — константа Эйлера–Машерони .

Соответствующая оценка была дана Джеффри Лагариасом в 2002 году, который доказал, что гипотеза Римана эквивалентна утверждению, что:

$\sigma (n)<H_{n}+\log(H_{n})e^{H_{n}}$

для любого натурального числа n > 1, где $H_{n}$ — номер n- й гармоники .

Гипотеза Римана также верна тогда и только тогда, когда выполнено неравенство

${\frac {n}{\varphi (n)}}<e^{\gamma }\log \log n+{\frac {e^{\gamma }(4+\gamma -\log 4\pi )}{\sqrt {\log n}}}$

верно для всех n ≥ 120569#, где φ ( n ) — функция Эйлера , а 120569# — произведение первых 120569 простых чисел.

Другой пример был найден Жеромом Франелем и расширен Ландау (см. Franel & Landau (1924) ). Гипотеза Римана эквивалентна нескольким утверждениям, показывающим, что члены последовательности Фэрея довольно регулярны. Одна из таких эквивалентностей такова: если Fn _{и до 1/1, то} — последовательность Фарея порядка n , начиная с 1/ n утверждение, что для всех ε > 0

$\sum _{i=1}^{m}|F_{n}(i)-{\tfrac {i}{m}}|=O\left(n^{{\frac {1}{2}}+\epsilon }\right)$

эквивалентно гипотезе Римана. Здесь

$m=\sum _{i=1}^{n}\varphi (i)$

— количество членов последовательности Фарея порядка n .

Например, из теории групп , если g ( n ) — функция Ландау , заданная максимальным порядком элементов симметричной группы Sn _n степени , то Массиас, Николас и Робин (1988) показали, что гипотеза Римана эквивалентна гипотезе Римана. граница

$\log g(n)<{\sqrt {\operatorname {Li} ^{-1}(n)}}$

для всех достаточно больших n .

Линделёфа и рост дзета

Гипотеза Римана имеет и другие более слабые последствия; одна из них — это гипотеза Линделефа о скорости роста дзета-функции на критической линии, которая гласит, что для любого ε > 0

$\zeta \left({\frac {1}{2}}+it\right)=O(t^{\varepsilon }),$

как $t\to \infty$.

Гипотеза Римана также предполагает достаточно резкие границы скорости роста дзета-функции в других областях критической полосы. Например, это подразумевает, что

$e^{\gamma }\leq \limsup _{t\rightarrow +\infty }{\frac {|\zeta (1+it)|}{\log \log t}}\leq 2e^{\gamma }$

${\frac {6}{\pi ^{2}}}e^{\gamma }\leq \limsup _{t\rightarrow +\infty }{\frac {1/|\zeta (1+it)|}{\log \log t}}\leq {\frac {12}{\pi ^{2}}}e^{\gamma }$

таким образом, скорость роста ζ (1 + it ) и обратная ей скорость будут известны с точностью до 2 раз.

о большом

Теорема о простых числах подразумевает, что в среднем разрыв между простым числом p и его последователем составляет log p . Однако некоторые промежутки между простыми числами могут быть намного больше, чем в среднем. Крамер доказал, что, принимая гипотезу Римана, каждый разрыв равен O ( √ p log p ). Это тот случай, когда даже лучшая оценка, которую можно доказать с помощью гипотезы Римана, намного слабее, чем то, что кажется верным: гипотеза Крамера подразумевает, что каждый разрыв равен O ((log p ) ² ), который хотя и больше среднего разрыва, но намного меньше границы, подразумеваемой гипотезой Римана. Численные данные подтверждают гипотезу Крамера.

эквивалентные

Было найдено множество утверждений, эквивалентных гипотезе Римана, однако ни одно из них пока не привело к значительному прогрессу в ее доказательстве (или опровержении). Вот некоторые типичные примеры. (Другие включают функцию делителя σ( n ).)

Критерий Рисса был предложен Риссом (1916) в том смысле, что граница

$-\sum _{k=1}^{\infty }{\frac {(-x)^{k}}{(k-1)!\zeta (2k)}}=O\left(x^{{\frac {1}{4}}+\epsilon }\right)$

выполняется для всех ε > 0 тогда и только тогда, когда верна гипотеза Римана. См. также критерий Харди–Литтлвуда .

Найман (1950) доказал, что гипотеза Римана верна тогда и только тогда, когда пространство функций вида

$f(x)=\sum _{\nu =1}^{n}c_{\nu }\rho \left({\frac {\theta _{\nu }}{x}}\right)$

где ρ ( z ) — дробная часть z , 0 ≤ θ _ν ≤ 1 , и

$\sum _{\nu =1}^{n}c_{\nu }\theta _{\nu }=0,$

плотно в гильбертовом пространстве L ² (0,1) функций, интегрируемых с квадратом на единичном интервале. Берлинг (1955) расширил это, показав, что дзета-функция не имеет нулей с действительной частью больше 1/ p тогда и только тогда, когда это функциональное пространство плотно в L. ^п (0,1). Этот критерий Наймана-Бёрлинга был усилен Баэсом-Дуарте. к случаю, когда $\theta _{\nu }\in \{1/k\}_{k\geq 1}$.

Салем (1953) показал, что гипотеза Римана верна тогда и только тогда, когда интегральное уравнение

$\int _{0}^{\infty }{\frac {z^{-\sigma -1}\varphi (z)}{{e^{x/z}}+1}}\,dz=0$

не имеет нетривиальных ограниченных решений $\varphi$ для $1/2<\sigma <1$.

Критерий Вейля — это утверждение, что положительность некоторой функции эквивалентна гипотезе Римана. С этим связан критерий Ли — утверждение, что положительность определенной последовательности чисел эквивалентна гипотезе Римана.

Спейзер (1934) доказал, что гипотеза Римана эквивалентна утверждению, что $\zeta '(s)$, производная от $\zeta (s)$, не имеет нулей в полосе

$0<\Re (s)<{\frac {1}{2}}.$

Что $\zeta (s)$ имеет только простые нули на критической линии, эквивалентно ее производной, не имеющей нулей на критической линии.

Последовательность Фэрея обеспечивает две эквивалентности, предложенные Джеромом Франелем и Эдмундом Ландау в 1924 году.

Константа де Брейна-Ньюмана, обозначаемая Λ и названная в честь Николааса Говерта де Брейна и Чарльза М. Ньюмана , определяетсякак уникальное действительное число такое, что функция

$H(\lambda ,z):=\int _{0}^{\infty }e^{\lambda u^{2}}\Phi (u)\cos(zu)\,du$,

который параметризован вещественным параметром λ , имеет комплексную переменную z и определяется с помощью суперэкспоненциально убывающей функции

$\Phi (u)=\sum _{n=1}^{\infty }(2\pi ^{2}n^{4}e^{9u}-3\pi n^{2}e^{5u})e^{-\pi n^{2}e^{4u}}$.

имеет только вещественные нули тогда и только тогда, когда λ ≥ Λ.Поскольку гипотеза Римана эквивалентна утверждению, что все нули H (0, z ) вещественны, гипотеза Римана эквивалентна гипотезе о том, что $\Lambda \leq 0$. Брэд Роджерс и Теренс Тао обнаружили, что эквивалентность на самом деле $\Lambda =0$ доказав, что ноль является нижней границей константы. Доказательство нуля также является верхней границей, поэтому доказывает гипотезу Римана. По состоянию на апрель 2020 года верхняя граница составляет $\Lambda \leq 0.2$.

гипотезы

используется обобщенная гипотеза Римана для L-рядов Дирихле или дзета-функции числовых полей В некоторых приложениях вместо только гипотезы Римана . Многие основные свойства дзета-функции Римана можно легко обобщить на все L-ряды Дирихле, поэтому вполне вероятно, что метод, доказывающий гипотезу Римана для дзета-функции Римана, также будет работать для обобщенной гипотезы Римана для L-функций Дирихле. Некоторые результаты, впервые доказанные с использованием обобщенной гипотезы Римана, позже получили безоговорочные доказательства без ее использования, хотя обычно это было намного сложнее. Многие из последствий в следующем списке взяты из работы Конрада (2010) .

• В 1913 году Грёнвалл Гаусса показал, что из обобщенной гипотезы Римана следует, что список мнимых квадратичных полей с номером класса 1 полон, хотя позже Бейкер, Старк и Хегнер дали безусловные доказательства этого без использования обобщенной гипотезы Римана.
• В 1917 году Харди и Литтлвуд показали, что из обобщенной гипотезы Римана следует гипотеза Чебышева о том, что
  $$\lim _{x\to 1^{-}}\sum _{p>2}(-1)^{(p+1)/2}x^{p}=+\infty ,$$
  который говорит, что простые числа 3 по модулю 4 в некотором смысле встречаются чаще, чем простые числа 1 по модулю 4. (Связанные результаты см. в разделе «Теорема о простых числах § Гонка простых чисел ».)
• В 1923 году Харди и Литтлвуд показали, что обобщенная гипотеза Римана подразумевает слабую форму гипотезы Гольдбаха для нечетных чисел: что каждое достаточно большое нечетное число является суммой трех простых чисел, хотя в 1937 году Виноградов дал безусловное доказательство. В 1997 году Дешуйерс , Эффингер, те Риле и Зиновьев показали, что из обобщенной гипотезы Римана следует, что каждое нечетное число больше 5 является суммой трех простых чисел. В 2013 году Харальд Хелфготт доказал троичную гипотезу Гольдбаха без зависимости от GRH после некоторых обширных вычислений, выполненных с помощью Дэвида Дж. Платта.
• В 1934 году Чоула показал, что из обобщенной гипотезы Римана следует, что первое простое число в арифметической прогрессии a mod m не превосходит Km. ² журнал( м ) ² для некоторой фиксированной константы K .
• В 1967 году Хули показал, что из обобщенной гипотезы Римана следует гипотеза Артина о примитивных корнях .
• Эйлера В 1973 году Вайнбергер показал, что из обобщенной гипотезы Римана следует, что список идонеальных чисел полон.
• Вайнбергер (1973) показал, что из обобщенной гипотезы Римана для дзета-функций всех полей алгебраических чисел следует, что любое числовое поле с номером класса 1 является либо евклидовым , либо полем мнимых квадратичных чисел с дискриминантом -19, -43, -67 или - 163.
• В 1976 году Г. Миллер показал, что обобщенная гипотеза Римана предполагает, что можно проверить, является ли число простым за полиномиальное время, с помощью теста Миллера . В 2002 году Маниндра Агравал, Нирадж Каял и Нитин Саксена безоговорочно доказали этот результат с помощью теста на простоту AKS .
• Одлыжко (1990) обсуждал, как можно использовать обобщенную гипотезу Римана для получения более точных оценок дискриминантов и чисел классов числовых полей.
• Оно и Саундарараджан (1997) показали, что из обобщенной гипотезы Римана следует, что целая квадратичная форма Рамануджана x ² + и ² + 10 з ² представляет все целые числа, которые он представляет локально, ровно с 18 исключениями.
• В 2021 году Александр (Алекс) Данн и Максим Радзивилл доказали гипотезу Паттерсона о кубических суммах Гаусса в предположении GRH.

Исключено среднее

Некоторые следствия RH также являются следствиями его отрицания и, таким образом, являются теоремами. В своем обсуждении теоремы Хекке, Дойринга, Морделла, Хейльбронна Айрленд и Розен (1990 , стр. 359) говорят:

Метод доказательства здесь поистине потрясающий. Если обобщенная гипотеза Римана верна, то и теорема верна. Если обобщенная гипотеза Римана неверна, то теорема верна. Таким образом, теорема верна!!

Следует внимательно понимать, что имеется в виду, когда говорят, что обобщенная гипотеза Римана ложна: следует точно указать, какой класс рядов Дирихле имеет контрпример.

Теорема Литтлвуда

Это касается знака ошибки в теореме о простых числах .Было вычислено, что π ( x ) < li ( x ) для всех x ≤ 10. ²⁵ (см. эту [[Теорема о простых числах#Таблица π ( x ), x /log x и li( x значение x )|таблица]]), и не известно , для которого π ( x ) > li( x ) .

В 1914 году Литтлвуд доказал, что существуют сколь угодно большие значения x , для которых

$\pi (x)>\operatorname {li} (x)+{\frac {1}{3}}{\frac {\sqrt {x}}{\log x}}\log \log \log x,$

и что существуют также сколь угодно большие значения x , для которых

$\pi (x)<\operatorname {li} (x)-{\frac {1}{3}}{\frac {\sqrt {x}}{\log x}}\log \log \log x.$

Таким образом, разность π ( x ) − li( x ) меняет знак бесконечное число раз. Число Скьюза — это оценка значения x, соответствующего первой смене знака.

Доказательство Литтлвуда разделено на два случая: RH предполагается ложным (около половины страницы Ingham 1932 , глава V), а RH считается истинным (около дюжины страниц). Станислав Кнаповский ( 1962 ) продолжил это исследование, написав статью о том, сколько раз $\Delta (n)$ меняет знак в интервале $\Delta (n)$.

Гаусса о

Это гипотеза Гаусса (впервые высказанная в статье 303 «Арифметических исследований» ) о том, что существует только конечное число мнимых квадратичных полей с заданным номером класса. Один из способов доказать это - показать, что в качестве дискриминанта D → −∞ номер класса h ( D ) → ∞ .

Следующая последовательность теорем, включающих гипотезу Римана, описана в Ireland & Rosen 1990 , стр. 358–361:

Теорема (Хекке; 1918 г.) — Пусть D <0 дискриминант мнимого поля квадратичных чисел K. — Предположим обобщенную гипотезу Римана для L -функций всех мнимых квадратичных характеров Дирихле. Тогда существует абсолютная константа C такая, что

$$h(D)>C{\frac {\sqrt {|D|}}{\log |D|}}.$$

Теорема (Дойринг; 1933 г.) — Если RH ложна, то h ( D ) > 1, если | Д | достаточно велик.

Теорема (Морделл; 1934 г.) — Если RH ложна, то h ( D ) → ∞ при D → −∞ .

Теорема (Хейльбронн; 1934 г.) — Если обобщенная RH неверна для L -функции некоторого мнимого квадратичного характера Дирихле, то h ( D ) → ∞ при D → −∞ .

(В работах Хекке и Хейльбронна встречаются только те L -функции , которые связаны с мнимыми квадратичными характерами, и только для этих L -функций предполагается, что GRH истинна или GRH ложна ; провал GRH для L -функция кубического характера Дирихле, строго говоря, означала бы, что GRH ложна, но это был не тот тип отказа GRH, который имел в виду Хейльбронн, поэтому его предположение было более ограниченным, чем просто GRH ложно .)

В 1935 году Карл Сигел усилил результат, никак не используя RH или GRH.

Эйлера

В 1983 году Дж. Л. Николас доказал, что

$$\varphi (n)<e^{-\gamma }{\frac {n}{\log \log n}}$$

для бесконечного числа n , где φ ( n ) — функция тотента Эйлера , а γ — константа Эйлера . Рибенбойм отмечает, что: «Метод доказательства интересен тем, что неравенство показывается сначала в предположении, что гипотеза Римана верна, а во-вторых, в противоположном предположении».

Обобщения и аналоги

серия Дирихле и другие

Гипотезу Римана можно обобщить, заменив дзета-функцию Римана формально аналогичными, но гораздо более общими глобальными L-функциями . В этом более широком контексте можно ожидать, что нетривиальные нули глобальных L -функций будут иметь действительную часть 1/2. Именно эти гипотезы, а не классическая гипотеза Римана только для одной дзета-функции Римана, объясняют истинную важность гипотезы Римана в математике.

Обобщенная гипотеза Римана распространяет гипотезу Римана на все L-функции Дирихле . В частности, из этого следует гипотеза о том, что нули Зигеля (нули L -функций между 1/2 и 1) не существуют.

Расширенная гипотеза Римана расширяет гипотезу Римана на все дзета-функции Дедекинда полей алгебраических чисел . Расширенная гипотеза Римана для абелева расширения рациональных чисел эквивалентна обобщенной гипотезе Римана. Гипотезу Римана можно распространить и на L -функции характеров Гекке числовых полей.

Большая гипотеза Римана распространяет ее на все автоморфные дзета-функции , такие как преобразования Меллина собственных форм Гекке .

функции многообразий над конечными полями

Артин (1924) ввел глобальные дзета-функции (квадратичных) функциональных полей и выдвинул для них гипотезу об аналоге гипотезы Римана, которая была доказана Хассе в случае рода 1 и Вейлем (1948) в целом. Например, тот факт, что сумма Гаусса квадратичного характера конечного поля размера q (с нечетным q ) имеет абсолютное значение ${\sqrt {q}}$ на самом деле является примером гипотезы Римана в условиях функционального поля. Это привело Вейля (1949) к предположению об аналогичном утверждении для всех алгебраических многообразий ; полученные в результате гипотезы Вейля были доказаны Пьером Делинем ( 1974 , 1980 ).

схем и их L-

Арифметические дзета-функции обобщают дзета-функции Римана и Дедекинда, а также дзета-функции многообразий над конечными полями на любую арифметическую схему или схему конечного типа над целыми числами. Арифметическая дзета-функция регулярной связной равномерной арифметической схемы кронекеровой размерности n может быть разложена на произведение соответствующим образом определенных L-факторов и вспомогательного фактора Жан-Пьера Серра ( 1969–1970 ). Предполагая функциональное уравнение и мероморфное продолжение, обобщенная гипотеза Римана для L-фактора утверждает, что его нули внутри критической полосы $\Re (s)\in (0,n)$ лежать на центральной линии. Соответственно, обобщенная гипотеза Римана для арифметической дзета-функции регулярной связной равномерной арифметической схемы утверждает, что ее нули внутри критической полосы лежат на вертикальных прямых. $\Re (s)=1/2,3/2,\dots ,n-1/2$ а его полюса внутри критической полосы лежат на вертикальных линиях $\Re (s)=1,2,\dots ,n-1$. Это известно для схем с положительной характеристикой и следует из Пьера Делиня ( 1974 , 1980 ), но остается совершенно неизвестным в нулевой характеристике.

Дзета-функции Сельберга

Основная статья: дзета-функция Сельберга

Сельберг (1956) ввел дзета-функцию Сельберга римановой поверхности. Они похожи на дзета-функцию Римана: у них есть функциональное уравнение и бесконечное произведение, подобное произведению Эйлера, но взятое по замкнутым геодезическим, а не по простым числам. Формула следов Сельберга является для этих функций аналогом явных формул теории простых чисел. Сельберг доказал, что дзета-функции Сельберга удовлетворяют аналогу гипотезы Римана, причем мнимые части их нулей связаны с собственными значениями оператора Лапласа римановой поверхности.

Ихара дзета-функции

Дзета -функция Ихара конечного графа является аналогом дзета-функции Сельберга , которая была впервые введена Ясутакой Ихара в контексте дискретных подгрупп 2х2 p-адической специальной линейной группы. Регулярный конечный граф является графом Рамануджана , математической моделью эффективных сетей связи, тогда и только тогда, когда его дзета-функция Ихара удовлетворяет аналогу гипотезы Римана, как было указано Т. Сунадой .

Монтгомери

Монтгомери (1973) выдвинул гипотезу о парной корреляции , согласно которой корреляционные функции (соответствующим образом нормализованных) нулей дзета-функции должны быть такими же, как и функции собственных значений случайной эрмитовой матрицы . Одлизко (1987) показал, что это подтверждается крупномасштабными численными расчетами этих корреляционных функций.

Монтгомери показал, что (при условии гипотезы Римана) по крайней мере 2/3 всех нулей являются простыми, и связанная с этим гипотеза состоит в том, что все нули дзета-функции являются простыми (или, в более общем смысле, не имеют нетривиальных целочисленных линейных отношений между их мнимыми частями). ). Дзета-функции Дедекинда полей алгебраических чисел, которые обобщают дзета-функцию Римана, часто имеют несколько комплексных нулей. Это связано с тем, что дзета-функции Дедекинда факторизуются как произведение степеней L-функций Артина , поэтому нули L-функций Артина иногда приводят к появлению кратных нулей дзета-функций Дедекинда. Другими примерами дзета-функций с несколькими нулями являются L-функции некоторых эллиптических кривых : они могут иметь несколько нулей в реальной точке их критической линии; гипотеза Берча-Суиннертона-Дайера предсказывает, что кратность этого нуля является рангом эллиптической кривой.

Другие дзета-функции

Существует множество других примеров дзета-функций с аналогами гипотезы Римана, некоторые из которых уже доказаны. Дзета-функции Госса функциональных полей имеют гипотезу Римана, доказанную Шитсом (1998) . Основная гипотеза теории Ивасавы , доказанная Барри Мазуром и Эндрю Уайлсом для круговых полей и Уайлсом для полностью вещественных полей , отождествляет нули p -адической L -функции с собственными значениями оператора, поэтому ее можно рассматривать как аналог гипотезы Гильберта–Пойа для p -адических L -функций .

Попытки

Несколько математиков обратились к гипотезе Римана, но ни одна из их попыток до сих пор не была принята в качестве доказательства. Уоткинс (2021) перечисляет некоторые неправильные решения.

Теория операторов

Основная статья: гипотеза Гильберта – Полиа

Гильберт и Полиа предположили, что одним из способов вывода гипотезы Римана было бы найти самосопряженный оператор , из существования которого следовало бы утверждение о вещественных частях нулей ζ ( s ), когда применялся критерий относительно действительных частей. собственные значения . Некоторую поддержку этой идеи дают несколько аналогов дзета-функций Римана, нули которых соответствуют собственным значениям некоторого оператора: нули дзета-функции многообразия над конечным полем соответствуют собственным значениям элемента Фробениуса на когомологий этальной группе , нули дзета-функции Сельберга являются собственными значениями оператора Лапласа римановой поверхности, а нули p-адической дзета-функции соответствуют собственным векторам действия Галуа на группах идеальных классов .

Одлыжко (1987) показал, что распределение нулей дзета-функции Римана имеет некоторые общие статистические свойства с собственными значениями случайных матриц, взятых из гауссовского унитарного ансамбля . Это дает некоторую поддержку гипотезе Гильберта-Пойа .

В 1999 году Майкл Берри и Джонатан Китинг предположили, что существует некое неизвестное квантование. ${\hat {H}}$ классического гамильтониана H = xp , так что

$$\zeta (1/2+i{\hat {H}})=0$$

и еще сильнее, что нули Римана совпадают со спектром оператора $1/2+i{\hat {H}}$. Это противоречит каноническому квантованию , которое приводит к принципу неопределенности Гейзенберга. $\sigma _{x}\sigma _{p}\geq {\frac {\hbar }{2}}$ и натуральные числа как спектр квантового гармонического осциллятора . Важным моментом является то, что гамильтониан должен быть самосопряженным оператором, чтобы квантование было реализацией программы Гильберта–Пойа. В связи с этой квантовомеханической проблемой Берри и Конн предположили, что обратный потенциал гамильтониана связан с полупроизводной функции

$$N(s)={\frac {1}{\pi }}\operatorname {Arg} \xi (1/2+i{\sqrt {s}})$$

тогда в подходе Гильберта-Пойя

$$V^{-1}(x)={\sqrt {4\pi }}{\frac {d^{1/2}N(x)}{dx^{1/2}}}.$$

Это дает гамильтониан, собственные значения которого представляют собой квадрат мнимой части нулей Римана, а также то, что функциональный определитель этого гамильтонова оператора представляет собой просто функцию Римана Xi . Фактически функция Римана Xi была бы пропорциональна функциональному определителю ( произведению Адамара )

$$\det(H+1/4+s(s-1))$$

$${\frac {\xi (s)}{\xi (0)}}={\frac {\det(H+s(s-1)+1/4)}{\det(H+1/4)}}.$$

Однако на практике этот оператор бесполезен, поскольку он включает в себя обратную функцию (неявную функцию) потенциала, но не сам потенциал.Аналогия с гипотезой Римана над конечными полями векторы, соответствующие нулям, может быть своего рода первой группой когомологий спектра предполагает, что гильбертово пространство, содержащее собственные Spec ( Z ) целых чисел. Денингер (1998) описал некоторые попытки найти такую ​​теорию когомологий.

Загер (1981) построил естественное пространство инвариантных функций на верхней полуплоскости, собственные значения которого под действием оператора Лапласа соответствуют нулям дзета-функции Римана, и заметил, что в том маловероятном случае, когда можно было бы показать существование подходящего положительного определенный внутренний продукт в этом пространстве, следует гипотеза Римана. Картье (1982) обсудил похожий пример, когда из-за странной ошибки компьютерная программа перечислила нули дзета-функции Римана как собственные значения одного и того же оператора Лапласа .

Шумайер и Хатчинсон (2011) рассмотрели некоторые попытки построить подходящую физическую модель, связанную с дзета-функцией Римана.

-

Теорема Ли-Янга утверждает, что все нули некоторых статистических сумм в статистической механике лежат на «критической линии», а их действительная часть равна 0, и это привело к некоторым предположениям о связи с гипотезой Римана.

Турана

Пал Туран ( 1948 ) показал, что если функции

$$\sum _{n=1}^{N}n^{-s}$$

не иметь нулей, если действительная часть s больше единицы, тогда

$$T(x)=\sum _{n\leq x}{\frac {\lambda (n)}{n}}\geq 0{\text{ for }}x>0,$$

где λ( n ) — функция Лиувилля , определяемая формулой (−1) ^р если n имеет r простых делителей. Он показал, что это, в свою очередь, будет означать, что гипотеза Римана верна. Но Хазельгроув (1958) доказал, что T ( x ) отрицательна для бесконечного числа x (а также опроверг тесно связанную с ней гипотезу Полиа ), а Борвейн, Фергюсон и Моссингхофф (2008) показали, что наименьший такой x равен 72  185  376  951  205 . Спира (1968) с помощью численного расчета показал, что приведенный выше конечный ряд Дирихле для N = 19 имеет нуль с действительной частью больше 1. Туран также показал, что несколько более слабое предположение - отсутствие нулей с действительной частью больше 1 + N. ^−1/2+е для больших N в конечном ряду Дирихле, указанном выше, также будет подразумевать гипотезу Римана, но Монтгомери (1983) показал, что для всех достаточно больших N эти ряды имеют нули с действительной частью больше 1 + (log log N )/(4 log N ) . Таким образом, результат Турана бессмысленно верен и не может помочь доказать гипотезу Римана.

Некоммутативная геометрия

Конн ( 1999 , 2000 ) описал связь между гипотезой Римана и некоммутативной геометрией и показал, что подходящий аналог формулы следа Сельберга для действия группы классов идель на пространство классов адели будет подразумевать гипотезу Римана. Некоторые из этих идей развиты в работе Лапидуса (2008) .

Гильбертово пространство целых функций

Луи де Бранж ( 1992 ) показал, что гипотеза Римана следует из условия положительности некоторого гильбертова пространства целых функций .Однако Конри и Ли (2000) показали, что необходимые условия положительности не выполняются. Несмотря на это препятствие, де Бранж продолжал работать над доказательством гипотезы Римана в том же духе, но это не получило широкого признания среди других математиков.

Квазикристаллы

Гипотеза Римана подразумевает, что нули дзета-функции образуют квазикристалл , распределение с дискретной поддержкой, преобразование Фурье которого также имеет дискретную поддержку. Дайсон (2009) предложил попытаться доказать гипотезу Римана путем классификации или, по крайней мере, изучения одномерных квазикристаллов.

функции моделей эллиптических кривых над числовыми полями

Когда кто-то переходит от геометрического измерения один, например, поля алгебраических чисел , к геометрическому измерению два, например, регулярной модели эллиптической кривой над числовым полем, двумерная часть обобщенной гипотезы Римана для арифметической дзета-функции модели имеет дело с полюсами дзета-функции. В размерности один исследование дзета-интеграла в диссертации Тейта не приводит к новой важной информации о гипотезе Римана. В отличие от этого, в измерении два работа Ивана Фесенко по двумерному обобщению диссертации Тейта включает интегральное представление дзета-интеграла, тесно связанного с дзета-функцией. В этой новой ситуации, невозможной в размерности один, полюса дзета-функции можно изучать с помощью дзета-интеграла и связанных с ним групп аделей. Сопутствующая гипотеза Фесенко ( 2010 ) о положительности четвертой производной граничной функции, связанной с дзета-интегралом, по существу подразумевает полюсную часть обобщенной гипотезы Римана. Сузуки ( 2011 ) доказали, что последнее вместе с некоторыми техническими предположениями влечет за собой гипотезу Фесенко.

Множественные дзета-функции

В доказательстве Делиня гипотезы Римана над конечными полями использовались дзета-функции многообразий произведений, нули и полюсы которых соответствуют суммам нулей и полюсов исходной дзета-функции, чтобы ограничить действительные части нулей исходной дзета-функции. По аналогии Курокава (1992) ввел несколько дзета-функций, нули и полюсы которых соответствуют суммам нулей и полюсов дзета-функции Римана. Чтобы ряд сходился, он ограничился суммами нулей или полюсов с неотрицательной мнимой частью. На данный момент известные границы нулей и полюсов кратных дзета-функций недостаточно сильны, чтобы дать полезные оценки нулей дзета-функции Римана.

Расположение нулей

Количество нулей

Функциональное уравнение в сочетании с принципом аргумента подразумевает, что количество нулей дзета-функции с мнимой частью между 0 и T определяется выражением

$N(T)={\frac {1}{\pi }}\mathop {\mathrm {Arg} } (\xi (s))={\frac {1}{\pi }}\mathop {\mathrm {Arg} } (\Gamma ({\tfrac {s}{2}})\pi ^{-{\frac {s}{2}}}\zeta (s)s(s-1)/2)$

для s =1/2+i T , где аргумент определяется путем его непрерывного изменения вдоль линии с Im( s )= T , начиная с аргумента 0 в точке ∞+i T . Это сумма большого, но хорошо понимаемого термина

${\frac {1}{\pi }}\mathop {\mathrm {Arg} } (\Gamma ({\tfrac {s}{2}})\pi ^{-s/2}s(s-1)/2)={\frac {T}{2\pi }}\log {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+7/8+O(1/T)$

и небольшой, но довольно загадочный термин

$S(T)={\frac {1}{\pi }}\mathop {\mathrm {Arg} } (\zeta (1/2+iT))=O(\log T).$

Таким образом, плотность нулей с мнимой частью вблизи T составляет около log( T )/(2 π ), а функция S описывает небольшие отклонения от этого значения. Функция S ( t ) скачет на 1 в каждом нуле дзета-функции, а при t ≥ 8 убывает монотонно между нулями с производной, близкой к −log t .

Трудджиан (2014) доказал, что если $T>e$, затем

$|N(T)-{\frac {T}{2\pi }}\log {\frac {T}{2\pi e}}|\leq 0.112\log T+0.278\log \log T+3.385+{\frac {0.2}{T}}$.

Карацуба (1996) доказал, что каждый интервал ( T , T + H ] для $H\geq T^{{\frac {27}{82}}+\varepsilon }$ содержит как минимум

$H(\log T)^{\frac {1}{3}}e^{-c{\sqrt {\log \log T}}}$

точки, в которых функция S ( t ) меняет знак.

Сельберг (1946) показал, что средние моменты четных степеней S определяются выражением

$\int _{0}^{T}|S(t)|^{2k}dt={\frac {(2k)!}{k!(2\pi )^{2k}}}T(\log \log T)^{k}+O(T(\log \log T)^{k-1/2}).$

Это говорит о том, что S ( T )/(log log T ) ^1/2 напоминает гауссову случайную величину со средним значением 0 и дисперсией 2 π ² ( Гош (1983) доказал этот факт).В частности | С ( Т ) | обычно где-то рядом (log log T ) ^1/2 , но иногда намного больше. Точный порядок роста S ( T ) неизвестен. Не произошло безусловного улучшения исходной оценки Римана S ( T )=O(log T ), хотя гипотеза Римана подразумевает немного меньшую оценку S ( T )=O(log T /log log T ). Истинный порядок величины может быть несколько меньше этого, поскольку случайные функции с тем же распределением, что и S ( T ), имеют тенденцию иметь рост порядка log( T ). ^1/2 . В другом направлении оно не может быть слишком маленьким: Сельберг (1946) показал, что S ( T ) ≠ o((log T ) ^1/3 /(логарифм Т ) ^7/3 ) и, приняв гипотезу Римана, Монтгомери показал, что S ( T ) ≠ o((log T ) ^1/2 /(логарифм Т ) ^1/2 ) .

Численные расчеты подтверждают, что S растет очень медленно: | С ( Т )| < 1 для Т < 280 , | С ( Т )| < 2 для T < 6 800 000 и наибольшее значение | С ( Т ) | найдено на данный момент не намного больше 3.

Оценка Римана S ( T ) = O(log T ) подразумевает, что промежутки между нулями ограничены, и Литтлвуд немного улучшил это, показав, что промежутки между их мнимыми частями стремятся к 0.

Адамара и де ля Валле

Адамар (1896 г.) и де ла Валле-Пуссен (1896 г.) независимо друг от друга доказали, что нули не могут лежать на прямой Re( s ) = 1. Вместе с функциональным уравнением и тем фактом, что не существует нулей с действительной частью больше 1, это показало, что все нетривиальные нули должны лежать внутри критической полосы 0 < Re( s ) < 1 . Это был ключевой шаг в их первых доказательствах теоремы о простых числах .

Оба исходных доказательства того, что дзета-функция не имеет нулей с вещественной частью 1, аналогичны и зависят от демонстрации того, что если ζ (1 + it ) обращается в нуль, то ζ (1 + 2 it ) сингулярна, что невозможно. Один из способов сделать это — использовать неравенство

$|\zeta (\sigma )^{3}\zeta (\sigma +it)^{4}\zeta (\sigma +2it)|\geq 1$

для σ > 1, t вещественное и рассматривая предел при σ → 1. Это неравенство следует из того, что мы берем действительную часть логарифма произведения Эйлера и видим, что

$|\zeta (\sigma +it)|=\exp \Re \sum _{p^{n}}{\frac {p^{-n(\sigma +it)}}{n}}=\exp \sum _{p^{n}}{\frac {p^{-n\sigma }\cos(t\log p^{n})}{n}},$

где сумма ведется по всем простым степеням p ^н , так что

$|\zeta (\sigma )^{3}\zeta (\sigma +it)^{4}\zeta (\sigma +2it)|=\exp \sum _{p^{n}}p^{-n\sigma }{\frac {3+4\cos(t\log p^{n})+\cos(2t\log p^{n})}{n}}$

что не менее 1, поскольку все члены суммы положительны в силу неравенства

$3+4\cos(\theta )+\cos(2\theta )=2(1+\cos(\theta ))^{2}\geq 0.$

Области без нуля

Самый обширный компьютерный поиск Платта и Трудджиана. для контрпримеров гипотезы Римана подтвердил ее для $|t|\leq 3.0001753328\cdot 10^{12}$. Кроме того, области без нулей известны как неравенства относительно σ + i t , которые могут быть нулями. Самая старая версия принадлежит Де ла Валле-Пуссену (1899–1900) , который доказал, что существует область без нулей, удовлетворяющая условию 1 − σ ≥. C / log( ) для некоторой положительной константы C. t Другими словами, нули не могут находиться слишком близко к линии σ = 1: вблизи этой линии существует область, свободная от нулей. Это было расширено несколькими авторами с использованием таких методов, как теорема Виноградова о среднем значении .

Самый последний документ Авторы Моссингхоффа, Трудджиана и Янга относятся к декабрю 2022 года и предоставляют четыре региона без нулей, которые улучшили предыдущие результаты Кевина Форда с 2002 года, самих Моссингхоффа и Трудгиана с 2015 года и небольшое улучшение Форда Пейсом Нильсеном с октября 2022 года:

$\sigma \geq 1-{\frac {1}{5.558691\log |t|}}$ в любое время $|t|\geq 2$,

$\sigma \geq 1-{\frac {1}{55.241(\log {|t|})^{2/3}(\log {\log {|t|}})^{1/3}}}$ в любое время $|t|\geq 3$ (крупнейший известный регион в границах $3.0001753328\cdot 10^{12}\leq |t|\leq \exp(64.1)\approx 6.89\cdot 10^{27}$),

$\sigma \geq 1-{\frac {0.04962-{\frac {0.0196}{1.15+\log 3+{\frac {1}{6}}\log t+\log \log t}}}{0.685+\log 3+{\frac {1}{6}}\log t+1.155\cdot \log \log t}}$ в любое время $|t|\geq 1.88\cdot 10^{14}$ (крупнейший известный регион в границах $\exp(64.1)\leq |t|\leq \exp(1000)\approx 1.97\cdot 10^{434}$) и

$\sigma \geq 1-{\frac {0.05035}{{\frac {27}{164}}(\log {|t|})+7.096}}+{\frac {0.0349}{({\frac {27}{164}}(\log {|t|})+7.096)^{2}}}$ в любое время $|t|\geq \exp(1000)$ (крупнейший известный регион в своей границе)

В статье также представлено улучшение второй безнулевой области, границы которой неизвестны из-за $|t|$ просто предполагается, что он «достаточно велик», чтобы выполнить требования доказательства статьи. Этот регион

$\sigma \geq 1-{\frac {1}{48.1588(\log {|t|})^{2/3}(\log {\log {|t|}})^{1/3}}}$.

Нули на критической линии

Харди (1914) и Харди и Литтлвуд (1921) показали, что на критической линии бесконечно много нулей, рассматривая моменты некоторых функций, связанных с дзета-функцией. Сельберг (1942) доказал, что на прямой лежит по крайней мере (малая) положительная часть нулей. Левинсон (1974) улучшил это значение до одной трети нулей, связав нули дзета-функции с нулями ее производной, а Конри (1989) улучшил это значение еще больше до двух пятых. В 2020 году эта оценка была увеличена до пяти двенадцатых Праттом, Роблесом, Захареску и Зейндлером. рассматривая расширенные смягчающие средства, которые могут учитывать производные дзета-функции более высокого порядка и связанные с ними суммы Клоостермана.

Большинство нулей лежат вблизи критической линии. Точнее, Бор и Ландау (1914) показали, что для любого положительного ε количество нулей с действительной частью не менее 1/2+ε и мнимой частью между -T и T равно $O(T)$. В сочетании с тем фактом, что нули критической полосы симметричны относительно критической линии и что общее число нулей в критической полосе равно $\Theta (T\log T)$, почти все нетривиальные нули находятся на расстоянии ε от критической линии. Ивич (1985) дает несколько более точных версий этого результата, называемых оценками нулевой плотности , которые ограничивают количество нулей в областях с мнимой частью не более T и действительной частью не менее 1/2+ε.

-

В 1914 году Годфри Гарольд Харди доказал, что $\zeta \left({\tfrac {1}{2}}+it\right)$ имеет бесконечно много действительных нулей.

Следующие две гипотезы Харди и Джона Иденсора Литтлвуда о расстоянии между действительными нулями $\zeta \left({\tfrac {1}{2}}+it\right)$ и от плотности нулей $\zeta \left({\tfrac {1}{2}}+it\right)$ на интервале $(T,T+H]$ для достаточно большого $T>0$, и $H=T^{a+\varepsilon }$ и с как можно меньшим значением $a>0$, где $\varepsilon >0$ является сколь угодно малым числом, открывают два новых направления в исследовании дзета-функции Римана:

1. Для любого $\varepsilon >0$ существует нижняя граница $T_{0}=T_{0}(\varepsilon )>0$ такой, что для $T\geq T_{0}$ и $H=T^{{\tfrac {1}{4}}+\varepsilon }$ интервал $(T,T+H]$ содержит нуль нечетного порядка функции $\zeta {\bigl (}{\tfrac {1}{2}}+it{\bigr )}$.

Позволять $N(T)$ быть общим количеством действительных нулей, и $N_{0}(T)$ — общее количество нулей нечетного порядка функции $~\zeta \left({\tfrac {1}{2}}+it\right)~$ лежащий на интервале $(0,T]~$.

2. Для любого $\varepsilon >0$ существует $T_{0}=T_{0}(\varepsilon )>0$ и некоторые $c=c(\varepsilon )>0$, такой, что для $T\geq T_{0}$ и $H=T^{{\tfrac {1}{2}}+\varepsilon }$ неравенство $N_{0}(T+H)-N_{0}(T)\geq cH$ это правда.

Сельберга

Основная статья: гипотеза дзета-функции Сельберга

Атле Сельберг ( 1942 ) исследовал проблему Харди–Литтлвуда 2 и доказал, что для любого ε > 0 существуют такие $T_{0}=T_{0}(\varepsilon )>0$ и c = c (ε) > 0, такие, что для $T\geq T_{0}$ и $H=T^{0.5+\varepsilon }$ неравенство $N(T+H)-N(T)\geq cH\log T$ это правда. Сельберг предположил, что это можно ужесточить до $H=T^{0.5}$. А. А. Карацуба ( 1984а , 1984б , 1985 ) доказал, что при фиксированном ε, удовлетворяющем условию 0 < ε < 0,001, достаточно большое T и $H=T^{a+\varepsilon }$, $a={\tfrac {27}{82}}={\tfrac {1}{3}}-{\tfrac {1}{246}}$, интервал ( T , T + H ) содержит не менее cH log( T ) действительных нулей дзета-функции Римана $\zeta \left({\tfrac {1}{2}}+it\right)$ и, следовательно, подтвердил гипотезу Сельберга. Оценки Сельберга и Карацубы не могут быть улучшены по порядку роста при T → ∞.

Карацуба (1992) доказал, что аналог гипотезы Сельберга верен почти для всех интервалов ( T , T + H ], $H=T^{\varepsilon }$, где ε — сколь угодно малое фиксированное положительное число. Метод Карацубы позволяет исследовать нули дзета-функции Римана на «сверхкоротких» интервалах критической линии, т. е. на интервалах ( T , T + H ), длина H которых растет медленнее любой, даже сколь угодно малой степени T , в частности, он доказал, что для любых заданных чисел ε, $\varepsilon _{1}$ удовлетворяющие условиям $0<\varepsilon ,\varepsilon _{1}<1$ почти все интервалы ( T , T + H ] для $H\geq \exp {\{(\log T)^{\varepsilon }\}}$ содержать по крайней мере $H(\log T)^{1-\varepsilon _{1}}$ нули функции $\zeta \left({\tfrac {1}{2}}+it\right)$. Эта оценка весьма близка к той, которая следует из гипотезы Римана.

Численные расчеты

Функция

$\pi ^{-{\frac {s}{2}}}\Gamma ({\tfrac {s}{2}})\zeta (s)$

имеет те же нули, что и дзета-функция в критической полосе, и является вещественной на критической линии из-за функционального уравнения, поэтому можно доказать существование нулей точно на действительной линии между двумя точками, проверив численно, что функция имеет противоположные значения. знаки в этих точках. Обычно пишут

$\zeta ({\tfrac {1}{2}}+it)=Z(t)e^{-i\theta (t)}$

Харди где Z-функция и тэта-функция Римана – Зигеля θ однозначно определяются этим и тем условием, что они являются гладкими вещественными функциями с θ (0) = 0.Найдя множество интервалов, в которых функция Z меняет знак, можно показать, что на критической прямой много нулей. Чтобы проверить гипотезу Римана с точностью до заданной мнимой части T нулей, необходимо также проверить, что в этой области нет дальнейших нулей за пределами линии. Это можно сделать, вычислив общее количество нулей в области с помощью метода Тьюринга и проверив, что оно совпадает с количеством нулей, найденных в строке. Это позволяет проверить гипотезу Римана вычислительно до любого желаемого значения T (при условии, что все нули дзета-функции в этой области просты и лежат на критической линии).

Эти расчеты также можно использовать для оценки $\pi (x)$ для конечных диапазонов $x$. Например, используя последний результат 2020 года (нули до высоты $3\times 10^{12}$), было показано, что

$|\pi (x)-\operatorname {li} (x)|<{\frac {1}{8\pi }}{\sqrt {x}}\log(x),\qquad {\text{for }}2657\leq x\leq 1.101\times 10^{26}.$

В общем случае это неравенство справедливо, если

$x\geq 2657$ и ${\frac {9.06}{\log {\log {x}}}}{\sqrt {\frac {x}{\log {x}}}}\leq T,$

где $T$ - наибольшее известное значение, такое, что гипотеза Римана верна для всех нулей $\rho$ с $\Im {\left(\rho \right)}\in \left(0,T\right]$.

Ниже приведены некоторые расчеты нулей дзета-функции, где «высотой» нуля является величина его мнимой части, а высота n- го нуля обозначается γ _n . На данный момент все проверенные нули находятся на критической линии и являются простыми. (Множество нулей может вызвать проблемы для алгоритмов поиска нулей, которые зависят от обнаружения смены знаков между нулями.) Таблицы нулей см. в Haselgrove & Miller (1960) или Odlyzko .

Год	Количество нулей	Автор
1859?	3	Б. Риман использовал формулу Римана-Зигеля (неопубликованную, но опубликованную в Siegel 1932 ).
1903	15	Дж. П. Грам (1903) использовал формулу Эйлера-Маклорена и открыл закон Грама . Он показал, что все 10 нулей с мнимой частью не более 50 лежат на критической линии с действительной частью 1/2, вычисляя сумму обратных 10-х степеней найденных им корней.
1914	79 ( γ n ≤ 200)	Р. Дж. Баклунд (1914) предложил лучший метод проверки того, что все нули до этой точки находятся на линии, путем изучения аргумента S ( T ) дзета-функции.
1925	138 ( γ n ≤ 300)	Дж. Хатчинсон (1925) обнаружил первое нарушение закона Грама в точке Грама g 126 .
1935	195	EC Titchmarsh (1935) использовал недавно заново открытую формулу Римана-Зигеля , которая намного быстрее, чем суммирование Эйлера-Маклорена. Это занимает около O( T 3/2 + е ) шаги для проверки нулей с мнимой частью меньше T , тогда как метод Эйлера–Маклорена требует около O( T 2 + е ) шаги.
1936	1041	Э. К. Титчмарш (1936) и Л. Дж. Комри были последними, кто нашел нули вручную.
1953	1104	А. М. Тьюринг (1953) нашел более эффективный способ проверить, что все нули до некоторой точки объясняются нулями на прямой, проверив, что Z имеет правильный знак в нескольких последовательных точках Грама, и используя тот факт, что S ( T ) имеет среднее значение 0. Это практически не требует дополнительной работы, поскольку знак Z в точках Грама уже известен из нахождения нулей и до сих пор является обычным используемым методом. Это было первое использование цифрового компьютера для вычисления нулей.
1956	15 000	Д. Х. Лемер (1956) обнаружил несколько случаев, когда дзета-функция имеет нули, которые находятся «только» на прямой: два нуля дзета-функции расположены настолько близко друг к другу, что между ними необычайно трудно найти смену знака. Это называется «феноменом Лемера» и сначала возникает в нулях с мнимыми частями 7005,063 и 7005,101, которые отличаются всего на 0,04, тогда как средний разрыв между другими нулями вблизи этой точки составляет около 1.
1956	25 000	Д. Х. Лемер
1958	35 337	Н. А. Меллер
1966	250 000	РС Леман
1968	3 500 000	Россер, Йохе и Шенфельд (1969) сформулировали правило Россера (описанное ниже).
1977	40 000 000	РП Брент
1979	81 000 001	РП Брент
1982	200 000 001	Р.П. Брент, Дж. ван де Люн , HJJ те Риле , DT Winter
1983	300 000 001	Дж. ван де Луне, HJJ в Риле
1986	1 500 000 001	ван де Люн, те Риле и Винтер (1986) предоставили некоторые статистические данные о нулях и привели несколько графиков Z в тех местах, где оно ведет себя необычно.
1987	Несколько крупных (~10 12 ) высота	А. М. Одлыжко ( 1987 ) вычислил меньшее количество нулей гораздо большей высоты, около 10. 12 , с высокой точностью для проверки гипотезы парной корреляции Монтгомери .
1992	Несколько крупных (~10 20 ) высота	А. М. Одлыжко ( 1992 ) вычислил 175 миллионов нулей высот около 10. 20 и еще несколько высот около 2 × 10 20 и дал подробное обсуждение результатов.
1998	10000 больших (~10 21 ) высота	А. М. Одлыжко ( 1998 ) вычислил несколько нулей высотой около 10. 21
2001	10 000 000 000	Дж. ван де Луне (неопубликовано)
2004	~ 900 000 000 000	С. Веденивски ( распределенные вычисления ZetaGrid )
2004	10 000 000 000 000 и несколько крупных (до ~10 24 ) высоты	X. Gourdon (2004) и Патрик Демишель использовали алгоритм Одлизко-Шенхаге . Они также проверили два миллиарда нулей на высоте 10. 13 , 10 14 , ..., 10 24 .
2020	12 363 153 437 138 до высоты 3 000 175 332 800	Платт и Трудджиан (2021) . Они также проверили работу Гурдона (2004) и других.

Грамм-пункты

Точка Грама — это точка на критической линии 1/2 + она , где дзета-функция действительна и не равна нулю. Используя выражение для дзета-функции на критической линии, ζ (1/2 + it ) = Z ( t )e ^{- iθ ( т )} , где функция Харди Z действительна для реального t , а θ — тэта-функция Римана–Зигеля , мы видим, что дзета действительна, когда sin( θ ( t )) = 0. Это означает, что θ ( t ) является целым числом кратен π , что позволяет довольно легко вычислить расположение точек Грамма путем обращения формулы для θ . Обычно они нумеруются как g _n для n = 0, 1, ..., где g _n — единственное решение θ ( t ) = n π .

Грэм заметил, что между любыми двумя точками Грама часто бывает ровно один ноль дзета-функции; Хатчинсон назвал это наблюдение законом Грама . Есть несколько других тесно связанных утверждений, которые также иногда называют законом Грама: например, (−1) ^н Z ( gn _Z ) обычно положителен, или ( t ) обычно имеет противоположный знак в последовательных точках Грама. Мнимые части γ _n первых нескольких нулей (синим цветом) и первых нескольких точек Грама g _n приведены в следующей таблице.

		г -1	с 1	г 0	с 2	г 1	с 3	г 2	с 4	г 3	с 5	г 4	с 6	г 5
0	3.436	9.667	14.135	17.846	21.022	23.170	25.011	27.670	30.425	31.718	32.935	35.467	37.586	38.999

Это полярный график первых 20 действительных значений r _n дзета-функции вдоль критической линии ζ (1/2 + it ), где t варьируется от 0 до 50. Значения r _n в этом диапазоне являются первыми . 10 нетривиальных нулей дзета-функции Римана и первые 10 точек Грама , каждая из которых помечена n . нанесено пятьдесят красных точек Между каждым r _n , а нули проецируются на концентрические пурпурные кольца, масштабированные так, чтобы показать относительное расстояние между их значениями t. Закон Грама гласит, что кривая обычно пересекает действительную ось один раз между нулями.

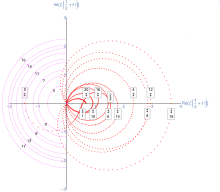
Первое нарушение закона Грама происходит в точке 127-го нуля и точке Грама g ₁₂₆ , которые находятся в «неправильном» порядке.

г 124	с 126	г 125	г 126	с 127	с 128	г 127	с 129	г 128
279.148	279.229	280.802	282.455	282.465	283.211	284.104	284.836	285.752

Точка Грама t называется хорошей, если дзета-функция положительна при 1/2 + it . Индексы «плохих» точек Грама, где Z имеет «неправильный» знак, равны 126, 134, 195, 211, ... (последовательность A114856 в OEIS ). Блок Грама — это интервал, ограниченный двумя хорошими точками Грама, причем все точки Грама между ними плохие. Уточнение закона Грама, названное правилом Россера, предложенное Россером, Йохе и Шенфельдом (1969), говорит, что блоки Грама часто имеют в себе ожидаемое количество нулей (так же, как количество интервалов Грама), даже несмотря на то, что некоторые из отдельных интервалов Грама в блоке может не быть ровно одного нуля. Например, интервал, ограниченный g ₁₂₅ и g _127, является блоком Грама, содержащим уникальную плохую точку Грама g ₁₂₆ , и содержит ожидаемое число нулей 2, хотя ни один из его двух интервалов Грама не содержит уникального нуля. Россер и др. проверил, что исключений из правила Россера в первых 3 миллионах нулей не было, хотя исключений из правила Россера бесконечно много по всей дзета-функции.

И правило Грама, и правило Россера гласят, что в некотором смысле нули не отклоняются слишком далеко от ожидаемого положения. Расстояние нуля от его ожидаемого положения контролируется определенной выше функцией S , которая растет крайне медленно: ее среднее значение имеет порядок (log log T ) ^1/2 , которое достигает 2 только для T около 10 ²⁴ . Это означает, что оба правила выполняются большую часть времени для малых T , но в конечном итоге часто нарушаются. Действительно, Трудджиан (2011) показал, что и закон Грама, и правило Россера не работают в положительной части случаев. Если быть конкретнее, ожидается, что примерно в 66% один ноль заключен в две последовательные точки Грама, но в 17% нет нуля и в 17% два нуля находятся в таком Грамм-интервале в долгосрочной перспективе Hanga (2020) .

гипотезы

Математические статьи о гипотезе Римана имеют тенденцию быть осторожными и уклончивыми в отношении ее истинности. Из авторов, выражающих мнение, большинство из них, например, Риман (1859) и Бомбьери (2000) , подразумевают, что они ожидают (или, по крайней мере, надеются), что это правда. К немногим авторам, выражающим серьезные сомнения по этому поводу, относятся Ивич (2008) , который перечисляет некоторые причины для скептицизма, и Литтлвуд (1962) , который категорически заявляет, что он считает это ложным, что нет никаких доказательств этого и нет вообразимой причины, по которой это могло бы произойти. быть правдой. Авторы обзорных статей ( Bombieri 2000 , Conrey 2003 и Sarnak 2005 ) сходятся во мнении, что доказательства в пользу этого убедительны, но не неопровержимы, так что, хотя это, вероятно, и верно, существуют обоснованные сомнения.

Некоторые аргументы за и против гипотезы Римана перечислены Сарнаком (2005) , Конри (2003) и Ивичем (2008) и включают следующее:

• Уже доказано несколько аналогов гипотезы Римана. Доказательство гипотезы Римана для многообразий над конечными полями, проведенное Делинем (1974) , возможно, является единственным сильным теоретическим аргументом в пользу гипотезы Римана. Это дает некоторые доказательства более общей гипотезы о том, что все дзета-функции, связанные с автоморфными формами, удовлетворяют гипотезе Римана, которая включает классическую гипотезу Римана как частный случай. Точно так же дзета-функции Сельберга удовлетворяют аналогу гипотезы Римана и в некотором смысле похожи на дзета-функцию Римана, имея функциональное уравнение и разложение в бесконечный продукт, аналогичное разложению в произведение Эйлера. Но есть и некоторые существенные различия; например, они не задаются рядом Дирихле. Гипотеза Римана для дзета-функции Госса была доказана Шитсом (1998) . В отличие от этих положительных примеров, некоторые дзета-функции Эпштейна не удовлетворяют гипотезе Римана, даже если они имеют бесконечное количество нулей на критической линии. Эти функции очень похожи на дзета-функцию Римана и имеют разложение в ряд Дирихле и функциональное уравнение , но те, которые, как известно, не соответствуют гипотезе Римана, не имеют произведения Эйлера и не имеют прямого отношения к автоморфным представлениям .
• На первый взгляд численная проверка того, что на прямой лежит много нулей, кажется убедительным доказательством этого. Но в аналитической теории чисел было много гипотез, подкрепленных существенными численными данными, которые оказались ложными. См. числа Скьюза , где первое исключение из правдоподобной гипотезы, связанной с гипотезой Римана, вероятно, происходит около 10 лет. пресловутый пример ³¹⁶ ; контрпример к гипотезе Римана с мнимой частью такого размера вышел бы далеко за рамки всего, что в настоящее время можно вычислить с использованием прямого подхода. Проблема в том, что на поведение часто влияют очень медленно возрастающие функции, такие как log log T , которые стремятся к бесконечности, но делают это настолько медленно, что это невозможно обнаружить с помощью вычислений. Такие функции встречаются в теории дзета-функции, управляющей поведением ее нулей; например, функция S ( T ) выше имеет средний размер около (log log T ) ^1/2 . Поскольку S ( T ) подскакивает как минимум на 2 при любом контрпримере к гипотезе Римана, можно было бы ожидать, что любые контрпримеры к гипотезе Римана начнут появляться только тогда, когда S ( T ) станет большим. Насколько было рассчитано, оно никогда не превышает 3, но известно, что оно неограничено, что позволяет предположить, что расчеты, возможно, еще не достигли области типичного поведения дзета-функции.
• Вероятностный аргумент Данжуа в пользу гипотезы Римана основано на наблюдении, что если µ( x ) является случайной последовательностью «1» и «−1» , то для каждого ε > 0 частичные суммы
  $$M(x)=\sum _{n\leq x}\mu (n)$$
  (значениями которых являются позиции в простом случайном блуждании ) удовлетворяют границе
  $$M(x)=O(x^{1/2+\varepsilon })$$
  с вероятностью 1 . Гипотеза Римана эквивалентна этой оценке для функции Мёбиуса ц и функции Мертенса M, полученной из нее таким же образом. Другими словами, гипотеза Римана в некотором смысле эквивалентна утверждению, что µ( x ) ведет себя как случайная последовательность подбрасываний монеты. Когда µ( x ) не равно нулю, его знак дает четность количества простых множителей x , поэтому неформально гипотеза Римана гласит, что четность количества простых множителей целого числа ведет себя случайным образом. Такие вероятностные аргументы в теории чисел часто дают правильный ответ, но их, как правило, очень трудно сделать строгими, и иногда они дают неправильный ответ на некоторые результаты, такие как теорема Майера .
• Расчеты Одлыжко (1987) показывают, что нули дзета-функции ведут себя очень похоже на собственные значения случайной эрмитовой матрицы , что позволяет предположить, что они являются собственными значениями некоторого самосопряженного оператора, что подразумевает гипотезу Римана. Все попытки найти такого оператора не увенчались успехом.
• Существует несколько теорем, таких как слабая гипотеза Гольдбаха для достаточно больших нечетных чисел, которые сначала были доказаны с использованием обобщенной гипотезы Римана, а затем показали, что их безоговорочная истинность. Это можно рассматривать как слабое доказательство обобщенной гипотезы Римана, поскольку некоторые из ее «предсказаний» верны.
• феномен Лемера , где два нуля иногда находятся очень близко, иногда дают повод не верить гипотезе Римана. Но можно было бы ожидать, что иногда это будет происходить случайно, даже если гипотеза Римана верна, а расчеты Одлизко показывают, что близлежащие пары нулей встречаются так же часто, как и предсказывает гипотеза Монтгомери .
• Паттерсон предполагает, что наиболее убедительной причиной гипотезы Римана для большинства математиков является надежда на то, что простые числа распределяются как можно более регулярно.

Ссылки

• Артин, Эмиль (1924), «Квадратные тела в области высших конгруэнций. II. Аналитическая часть», Mathematical Journal , 19 (1): 207–246, doi : 10.1007/BF01181075 , S2CID   117936362
• Баклунд, Р.Дж. (1914), «О нулях ζ ( s функции Римана )» , CR Acad. наук. Париж , 158 : 1979–1981.
• Берлинг, Арне (1955), «Проблема замыкания, связанная с дзета-функцией Римана», Труды Национальной академии наук Соединенных Штатов Америки , 41 (5): 312–314, Бибкод : 1955PNAS ... 41 ..312B , doi : 10.1073/pnas.41.5.312 , MR   0070655 , PMC   528084 , PMID   16589670
• Бьёрнер, Андерс (2011), «Клеточный комплекс в теории чисел», Успехи в прикладной математике , 46 (1–4): 71–85, arXiv : 1101.5704 , doi : 10.1016/j.aam.2010.09.007
• Бор, Х .; Ландау, Э. (1914), «Теорема о рядах Дирихле с применением к ζ -функции и L -функциям», Rendiconti del Circolo Matematico di Palermo , 37 (1): 269–272, doi : 10.1007/BF03014823 , S2CID   121145912
• Бомбьери, Энрико (2000), Гипотеза Римана - официальное описание проблемы (PDF) , Институт математики Клэя , заархивировано из оригинала (PDF) 22 декабря 2015 г. , получено 25 октября 2008 г. Перепечатано в ( Borwein et al. 2008). ).
• Борвейн, Питер ; Чой, Стивен; Руни, Брендан; Вейратмюллер, Андреа, ред. (2008), Гипотеза Римана: ресурс как для любителей, так и для виртуозов , Книги CMS по математике, Нью-Йорк: Springer, doi : 10.1007/978-0-387-72126-2 , ISBN  978-0-387-72125-5
• Борвейн, Питер ; Фергюсон, Рон; Моссингхофф, Майкл Дж. (2008), «Изменение знака в суммах функции Лиувилля», Mathematics of Computation , 77 (263): 1681–1694, Бибкод : 2008MaCom..77.1681B , doi : 10.1090/S0025-5718-08 -02036-Х , МР   2398787
• де Бранж, Луи (1992), «Сходимость произведений Эйлера», Журнал функционального анализа , 107 (1): 122–210, doi : 10.1016/0022-1236(92)90103-P , MR   1165869
• Броган, Кевин (2017), Эквиваленты гипотезы Римана , Cambridge University Press, ISBN  978-1108290784
• Бертон, Дэвид М. (2006), Элементарная теория чисел , Tata McGraw-Hill Publishing Company Limited, ISBN  978-0-07-061607-3
• Картье, П. (1982), «Как гипотеза Римана не была доказана», Семинар по теории чисел, Париж, 1980–81 (Париж, 1980/1981) , Progr. Матем., вып. 22, Бостон, Массачусетс: Birkhäuser Boston, стр. 35–48, МР   0693308
• Конн, Ален (1999), «Формула следа в некоммутативной геометрии и нули дзета-функции Римана», Selecta Mathematica , New Series, 5 (1): 29–106, arXiv : math/9811068 , doi : 10.1007/s000290050042 , МР   1694895 , S2CID   55820659
• Конн, Ален (2000), «Некоммутативная геометрия и дзета-функция Римана», Математика: границы и перспективы , Провиденс, Род-Айленд: Американское математическое общество , стр. 35–54, MR   1754766
• Конн, Ален (2016), «Очерк гипотезы Римана», в Нэше, Дж. Ф .; Рассиас, Майкл (ред.), Открытые проблемы по математике , Нью-Йорк: Springer, стр. 225–257, arXiv : 1509.05576 , doi : 10.1007/978-3-319-32162-2_5.
• Конри, Дж. Б. (1989), «Более двух пятых нулей дзета-функции Римана находятся на критической линии» , Дж. Рейн Ангью. Математика. , 1989 (399): 1–26, doi : 10.1515/crll.1989.399.1 , MR   1004130 , S2CID   115910600
• Конри, Дж. Брайан (2003), «Гипотеза Римана» (PDF) , Уведомления Американского математического общества : 341–353. Перепечатано в ( Borwein et al. 2008 ).
• Конри, Джей Би ; Ли, Сянь-Цзинь (2000), «Заметка о некоторых условиях положительности, связанных с дзета- и L-функциями», International Mathematics Research Notions , 2000 (18): 929–940, arXiv : math/9812166 , doi : 10.1155/S1073792800000489 , МР   1792282 , S2CID   14678312
• Делинь, Пьер (1974), «Гипотеза Вейля. I» , Publications Mathématiques de l'IHÉS , 43 : 273–307, doi : 10.1007/BF02684373 , MR   0340258 , S2CID   123139343
• Делинь, Пьер (1980), «Гипотеза Вейля: II» , Publications Mathématiques de l'IHÉS , 52 : 137–252, doi : 10.1007/BF02684780 , S2CID   189769469
• Денингер, Кристофер (1998), «Некоторые аналогии между теорией чисел и динамическими системами в расслоенных пространствах» , Труды Международного конгресса математиков, Vol. I (Берлин, 1998) , Documenta Mathematica, стр. 163–186, MR   1648030.
• Дудек, Адриан В. (21 августа 2014 г.), «О гипотезе Римана и разнице между простыми числами», Международный журнал теории чисел , 11 (3): 771–778, arXiv : 1402.6417 , Bibcode : 2014arXiv1402.6417D , doi : 10.1142/S1793042115500426 , ISSN   1793-0421 , S2CID   119321107
• Дайсон, Фриман (2009), «Птицы и лягушки» (PDF) , Уведомления Американского математического общества , 56 (2): 212–223, MR   2483565
• Эдвардс, HM (1974), Дзета-функция Римана , Нью-Йорк: Dover Publications , ISBN  978-0-486-41740-0 , МР   0466039
• Фесенко, Иван (2010), «Анализ на арифметических схемах. II», Журнал K-теории , 5 (3): 437–557, doi : 10.1017/is010004028jkt103
• Форд, Кевин (2002), «Интеграл Виноградова и границы дзета-функции Римана», Труды Лондонского математического общества , третья серия, 85 (3): 565–633, arXiv : 1910.08209 , doi : 10.1112/S0024611502013655 , MR   19368 14 , S2CID   121144007
• Франель, Дж .; Ландау, Э. (1924), «Сюиты Фарея и проблемы премьер-министров» (Франель, 198–201); «Замечания г-на Франеля к вышеупомянутому трактату (Ландау, 202–206)», Göttinger Nachrichten : 198–206.
• Гош, Амит (1983), «О дзета-функции Римана — теоремы о среднем значении и распределении |S(T)|», J. Number Theory , 17 : 93–102, doi : 10.1016/0022-314X(83) 90010-0
• Гурдон, Ксавье (2004), 10 ¹³ первые нули дзета-функции Римана и вычисление нулей на очень большой высоте (PDF)
• Грам, Дж. П. (1903), «Примечание о нулях ζ ( s функции Римана ) , Acta Mathematica , 27 : 289–304, doi : 10.1007/BF02421310 , S2CID   115327214
• Адамар, Жак (1896), «О распределении нулей функции ζ ( s ) и ее арифметических следствиях», Bulletin de la Société Mathématique de France , 14 : 199–220, doi : 10.24033/bsmf.545 Перепечатано в ( Борвейн и др .
• Ханга, Каталин (2020), Случайные матричные модели для закона Грама (доктор философии), Йоркский университет
• Харди, GH (1914), «О нулях функции ζ ( s ) Римана» , CR Acad. наук. Paris , 158 : 1012–1014, JFM   45.0716.04 Перепечатано в ( Borwein et al. 2008 ).
• Харди, штат Джорджия ; Литтлвуд, Дж. Э. (1921), «Нули дзета-функции Римана на критической линии» , Math. З. , 10 (3–4): 283–317, doi : 10.1007/BF01211614 , S2CID   126338046
• Хазельгроув, CB (1958), «Опровержение гипотезы Полиа», Mathematika , 5 (2): 141–145, doi : 10.1112/S0025579300001480 , ISSN   0025-5793 , MR   0104638 , Zbl   0085.27102 . ( Борвейн и др. . 2008 ).
• Хазелгроув, Коннектикут ; Миллер, JCP (1960), Таблицы дзета-функции Римана , Математические таблицы Королевского общества, Vol. 6, Издательство Кембриджского университета , ISBN  978-0-521-06152-0 , МР   0117905 Отзыв
• Хатчинсон, Дж.И. (1925), «О корнях дзета-функции Римана», Труды Американского математического общества , 27 (1): 49–60, doi : 10.2307/1989163 , JSTOR   1989163
• Ингэм, А.Е. (1932), Распределение простых чисел , Кембриджские трактаты по математике и математической физике, том. 30, Издательство Кембриджского университета . Перепечатано 1990 г., ISBN   978-0-521-39789-6 , МР 1074573
• Ирландия, Кеннет; Розен, Майкл (1990), Классическое введение в современную теорию чисел (второе издание) , Нью-Йорк: Springer , ISBN  0-387-97329-Х
• Ивич, А. (1985), Дзета-функция Римана , Нью-Йорк: John Wiley & Sons , ISBN  978-0-471-80634-9 , MR   0792089 (перепечатано Dover, 2003 г.)
• Ивич, Александар (2008), «О некоторых причинах сомнений в гипотезе Римана», в Борвейн, Питер; Чой, Стивен; Руни, Брендан; Вейратмюллер, Андреа (ред.), Гипотеза Римана: ресурс как для любителей, так и для виртуозов , Книги CMS по математике, Нью-Йорк: Springer, стр. 131–160, arXiv : math.NT/0311162 , ISBN  978-0-387-72125-5
• Карацуба А.А. (1984а), "Нули функции ζ ( s ) на коротких интервалах критической линии", Изв. Акад. Наук СССР, сер. Мат. (на русском языке), 48 (3): 569–584, МР   0747251
• Карацуба А.А. (1984б), "Распределение нулей функции ζ (1/2 + it )", Изв. Акад. Наук СССР, сер. Мат. (на русском языке), 48 (6): 1214–1224, МР   0772113
• Карацуба А.А. (1985), "Нули дзета-функции Римана на критической прямой", Тр. Матем. Инст. Стеклов. (на русском языке) (167): 167–178, МР   0804073
• Карацуба А.А. (1992), "О числе нулей дзета-функции Римана, лежащих почти на всех коротких интервалах критической линии", Изв. Росс. Акад. Наук, сер. Мат. (на русском языке), 56 (2): 372–397, Бибкод : 1993ИзМат..40..353К , doi : 10.1070/IM1993v040n02ABEH002168 , MR   1180378
• Карацуба, А.А. ; Воронин, С.М. (1992), Дзета-функция Римана , Изложения де Грюйтера по математике, вып. 5, Берлин: Вальтер де Грюйтер и компания, номер документа : 10.1515/9783110886146 , ISBN.  978-3-11-013170-3 , МР   1183467
• Китинг, Джонатан П.; Снайт, Северная Каролина (2000), «Теория случайных матриц и ζ (1/2 + it )», Communications in Mathematical Physics , 214 (1): 57–89, Bibcode : 2000CMaPh.214...57K , doi : 10.1007/ s002200000261 , MR   1794265 , S2CID   11095649
• Кнаповски, С. (1962), "Об изменении знака разности $\pi (x)-\operatorname {li} x$", Acta Arithmetica , 7 : 107–119, doi : 10.4064/aa-7-2-107-119 , MR   0133308
• Кнауф, Андреас (1999), «Теория чисел, динамические системы и статистическая механика», Обзоры по математической физике , 11 (8): 1027–1060, Бибкод : 1999RvMaP..11.1027K , doi : 10.1142/S0129055X99000325 , MR   1714352
• фон Кох, Нильс Хельге (1901), «О распределении простых чисел» , Acta Mathematica , 24 : 159–182, doi : 10.1007/BF02403071 , S2CID   119914826
• Курокава, Нобусигэ (1992), «Множественные дзета-функции: пример», Дзета-функции в геометрии (Токио, 1990) , Adv. Стад. Чистая математика., вып. 21, Токио: Кинокуния, стр. 219–226, MR   1210791.
• Лапидус, Мишель Л. (2008), В поисках нулей Римана , Провиденс, Род-Айленд: Американское математическое общество, doi : 10.1090/mbk/051 , ISBN  978-0-8218-4222-5 , МР   2375028
• Лаврик, А.Ф. (2001) [1994], «Дзета-функция» , Энциклопедия математики , EMS Press
• Лемер, Д.Х. (1956), «Расширенное вычисление дзета-функции Римана», Mathematika , 3 (2): 102–108, doi : 10.1112/S0025579300001753 , MR   0086083
• Лейхтнам, Эрик (2005), «Приглашение к работе Денингера над арифметическими дзета-функциями», Геометрия, спектральная теория, группы и динамика , Contemp. Матем., вып. 387, Провиденс, Род-Айленд: Амер. Математика. Soc., стр. 201–236, doi : 10.1090/conm/387/07243 , MR   2180209 .
• Левинсон, Н. (1974), «Более трети нулей дзета-функции Римана находятся на σ = 1/2», Advance in Mathematics , 13 (4): 383–436, doi : 10.1016/0001-8708 (74)90074-7 , МР   0564081
• Литтлвуд, Дж. Э. (1962), «Гипотеза Римана», Ученый размышляет: антология частично выработанных идей , Нью-Йорк: Основные книги.
• ван де Люн, Дж.; те Риле, HJJ ; Винтер, Д.Т. (1986), «О нулях дзета-функции Римана в критической полосе. IV», Mathematics of Computation , 46 (174): 667–681, doi : 10.2307/2008005 , JSTOR   2008005 , MR   0829637
• Массиас, Ж.-П.; Николя, Жан-Луи ; Робин, Г. (1988), «Асимптотическая оценка максимального порядка элемента симметричной группы» , Acta Arithmetica , 50 (3): 221–242, doi : 10.4064/aa-50-3-221-242 , МР   0960551
• Мазур, Барри; Штейн, Уильям (2015), Простые числа и гипотеза Римана
• Монтгомери, Хью Л. (1973), «Парная корреляция нулей дзета-функции», Аналитическая теория чисел , Proc. Симпозиумы. Чистая математика., вып. XXIV, Провиденс, Род-Айленд: Американское математическое общество, стр. 181–193, MR   0337821. Перепечатано в ( Borwein et al. 2008 ).
• Монтгомери, Хью Л. (1983), «Нули приближений к дзета-функции», в Эрдеш, Пол (редактор), Исследования по чистой математике. Памяти Пауля Турана , Базель, Бостон, Берлин: Birkhäuser, стр. 497–506, ISBN.  978-3-7643-1288-6 , МР   0820245
• Монтгомери, Хью Л .; Воган, Роберт К. (2007), Мультипликативная теория чисел I. Классическая теория , Кембриджские исследования по высшей математике, том. 97, Издательство Кембриджского университета . ISBN   978-0-521-84903-6
• Хорошо, Томас Р. (1999), «Новые максимальные простые пробелы и первые вхождения» , Mathematics of Computation , 68 (227): 1311–1315, Бибкод : 1999MaCom..68.1311N , doi : 10.1090/S0025-5718-99- 01065-0 , МР   1627813 .
• Найман, Бертил (1950), Об одномерной группе трансляции и полугруппе в некоторых функциональных пространствах , докторская диссертация, Университет Упсалы: Университет Упсалы, MR   0036444
• Одлизко, А.М. ; HJ , Риле те Journal für die reine und angewandte Mathematik, 1985 (357): 138–160, doi:10.1515/crll.1985.357.138, MR 0783538, S2CID 13016831​​​​​​​​​​​​из оригинала от 11 июля 2012 г.
• Одлизко, AM (1987), «О распределении расстояний между нулями дзета-функции», Mathematics of Computation , 48 (177): 273–308, doi : 10.2307/2007890 , JSTOR   2007890 , MR   0866115
• Одлызко, AM (1990), «Оценки дискриминантов и соответствующие оценки для чисел классов, регуляторов и нулей дзета-функций: обзор недавних результатов» , Séminaire de Théorie des Nombres de Bordeaux , Série 2, 2 (1): 119– 141, номер номера : 10.5802/jtnb.22 , MR   1061762
• Одлизко, А.М. (1992), 10 ²⁰ -й ноль дзета-функции Римана и 175 миллионов ее соседей (PDF) В этой неопубликованной книге описывается реализация алгоритма и подробно обсуждаются результаты.
• Одлизко, AM (1998), 10 ²¹ первый ноль дзета-функции Римана (PDF)
• Оно, Кен ; Саундараджан, К. (1997), « Трнарная квадратичная форма Раманари», the Mathematicae , Inventions 415–454, : 1997O , DOI : 10.1007 / бибкод s0   122314044
• Паттерсон, С.Дж. (1988), Введение в теорию дзета-функции Римана , Кембриджские исследования по высшей математике, том. 14, Издательство Кембриджского университета, номер домена : 10.1017/CBO9780511623707 , ISBN.  978-0-521-33535-5 , МР   0933558
• Платт, Дэйв; Трудджиан, Тим (январь 2021 г.): «Гипотеза Римана верна с точностью до $3\cdot 10^{12}$», Бюллетень Лондонского математического общества , 53 (3), Wiley: 792–797, arXiv : 2004.09765 , doi : 10.1112/blms.12460 , S2CID   234355998
• Радзеевский, Мацей (2007), «Независимость дзета-функций Гекке конечного порядка от нормальных полей», Труды Американского математического общества , 359 (5): 2383–2394, doi : 10.1090/S0002-9947-06-04078-5 , MR   2276625 , Существует бесконечно много неизоморфных полей алгебраических чисел, у которых дзета-функции Дедекинда имеют бесконечное количество нетривиальных кратных нулей.
• Рибенбойм, Пауло (1996), Новая книга рекордов простых чисел , Нью-Йорк: Springer , ISBN  0-387-94457-5
• Риман, Бернхард (1859), «О количестве простых чисел заданного размера» , Ежемесячные отчеты Берлинской академии . В собрании сочинений Тойбнера, Лейпциг (1892 г.), перепечатано Дувром, Нью-Йорк (1953 г.). Оригинальная рукопись (с английским переводом). Перепечатано в ( Борвейн и др., 2008 г. ) и ( Эдвардс, 1974 г. ).
• Ризель, Ганс ; Гёль, Гуннар (1970), «Некоторые вычисления, связанные с формулой простых чисел Римана», Mathematics of Computation , 24 (112): 969–983, doi : 10.2307/2004630 , JSTOR   2004630 , MR   0277489
• Рисс, М. (1916), «О гипотезе Римана», Acta Mathematica , 40 : 185–190, doi : 10.1007/BF02418544
• Робин, Г. (1984), «Большие значения функции суммы делителей и гипотеза Римана», Журнал чистой и прикладной математики , девятая серия, 63 (2): 187–213, MR   0774171
• Роджерс, Брэд; Тао, Теренс (2020), «Константа де Брейна-Ньюмана неотрицательна», Forum of Mathematics , 8 : e6, 62, arXiv : 1801.05914 , doi : 10.1017/fmp.2020.6 , MR   4089393 ; см. также анонс в блоге Тао , 19 января 2018 г.
• Россер, Дж. Баркли ; Йохе, Дж. М.; Шенфельд, Лоуэлл (1969), «Строгие вычисления и нули дзета-функции Римана. (С обсуждением)», Information Processing 68 (Proc. IFIP Congress, Эдинбург, 1968), Vol. Т. 1: Математика, программное обеспечение , Амстердам: Северная Голландия, стр. 70–76, MR   0258245.
• Рудин, Уолтер (1973), Функциональный анализ, 1-е издание (январь 1973 г.) , Нью-Йорк: McGraw-Hill , ISBN  0-070-54225-2
• Салем, Рафаэль (1953), «О предложении, эквивалентном гипотезе Римана», Les Comptes de l'Académie des Sciences , 236 : 1127–1128, MR   0053148
• Сарнак, Питер (2005), Проблемы тысячелетия: гипотеза Римана (2004) (PDF) , Институт математики Клэя , получено 28 июля 2015 г. Перепечатано в ( Borwein et al. 2008 ).
• Шенфельд, Лоуэлл (1976), «Более точные оценки для функций Чебышева θ ( x ) и ψ ( x ). II», Mathematics of Computation , 30 (134): 337–360, doi : 10.2307/2005976 , JSTOR   2005976 , MR   0457374
• Шумайер, Дэниел; Хатчинсон, Дэвид А.В. (2011), «Физика гипотезы Римана», Обзоры современной физики , 83 (2): 307–330, arXiv : 1101.3116 , Bibcode : 2011RvMP...83..307S , doi : 10.1103/RevModPhys .83.307 , S2CID   119290777
• Сельберг, Атле (1942), «О нулях дзета-функции Римана», SKR. Норвежское видео. акад. Осло I. , 10 : 59 стр., MR   0010712.
• Сельберг, Атле (1946), «Вклад в теорию дзета-функции Римана», Arch. Математика. Натурвид. , 48 (5): 89–155, МР   0020594
• Сельберг, Атле (1956), «Гармонический анализ и разрывные группы в слабо симметричных римановых пространствах с приложениями к рядам Дирихле», J. Indian Math. Соц. , Новая серия, 20 : 47–87, МР   0088511
• Серр, Жан-Пьер (1969–1970), «Локальные факторы дзета-функций алгебраических многообразий (определения и гипотезы)» , Семинар Деланжа-Пизо-Пуату , 19
• Шитс, Джеффри Т. (1998), «Гипотеза Римана для дзета-функции Госса для F _q [T]», Journal of Number Theory , 71 (1): 121–157, arXiv : math/9801158 , doi : 10.1006/ jnth.1998.2232 , MR   1630979 , S2CID   119703557
• Сигел, CL (1932), «О наследии Римана в аналитической теории чисел», источниковедение по истории математики. И Физ. Отдел B: Исследования 2 : 45–80 , перепечатано в сборнике статей, том 1. Берлин: Springer-Verlag, 1966.
• Спейзер, Андреас (1934), «Геометрическая информация о дзета-функции Римана» , Mathematical Annals , 110 : 514–521, doi : 10.1007/BF01448042 , JFM   60.0272.04 , S2CID   119413347 , заархивировано из оригинала в 2015-06 гг. -27
• Спира, Роберт (1968), «Нули секций дзета-функции. II», Mathematics of Computation , 22 (101): 163–173, doi : 10.2307/2004774 , JSTOR   2004774 , MR   0228456
• Стейн, Уильям ; Мазур, Барри (2007), Что такое гипотеза Римана? (PDF) , заархивировано из оригинала (PDF) 27 марта 2009 г.
• Судзуки, Масатоши (2011), «Положительность некоторых функций, связанных с анализом на эллиптических поверхностях», Journal of Number Theory , 131 (10): 1770–1796, doi : 10.1016/j.jnt.2011.03.007
• Титчмарш, Эдвард Чарльз (1935), «Нули дзета-функции Римана», Труды Лондонского королевского общества. Серия A, Математические и физические науки , 151 (873), Королевское общество: 234–255, Bibcode : 1935RSPSA.151..234T , doi : 10.1098/rspa.1935.0146 , JSTOR   96545 , S2CID   263711590
• Титчмарш, Эдвард Чарльз (1936), «Нули дзета-функции Римана», Труды Лондонского королевского общества. Серия A, Математические и физические науки , 157 (891), Королевское общество: 261–263, arXiv : 1004.4143 , Бибкод : 1936RSPSA.157..261T , doi : 10.1098/rspa.1936.0192 , JSTOR   96692
• Титчмарш, Эдвард Чарльз (1986), Теория дзета-функции Римана (2-е изд.), The Clarendon Press Oxford University Press, ISBN  978-0-19-853369-6 , МР   0882550
• Трудджиан, Тимоти С. (2014), «Улучшенная верхняя оценка аргумента дзета-функции Римана на критической линии II», J. Number Theory , 134 : 280–292, arXiv : 1208.5846 , doi : 10.1016/j. jnt.2013.07.017
• Трудджиан, Тимоти (2011), «Об успехе и неудаче закона Грама и правила Россера», Acta Arithmetica , 125 (3): 225–256, doi : 10.4064/aa148-3-2
• Туран, Пауль (1948), «О некоторых аппроксимативных полиномах Дирихле в теории дзета-функции Римана», Danske Vid. Сельск. Мат.-физ. Медд. , 24 (17): 36, MR   0027305 Перепечатано в ( Borwein et al. 2008 ).
• Тьюринг, Алан М. (1953), «Некоторые вычисления дзета-функции Римана», Труды Лондонского математического общества , третья серия, 3 : 99–117, doi : 10.1112/plms/s3-3.1.99 , MR   0055785
• де ла Валле-Пуссен, Ч.Ж. (1896), «Аналитические исследования по теории простых чисел», Анн. Соц. наук. Брюссель , 20 : 183–256.
• де ла Валле-Пуссен, Ч.Ж. (1899–1900), “О функции ζ ( s ) Римана и числе простых чисел, меньших заданного предела”, Mem. Короны Акад. наук. Бельгия. , 59 (1) Перепечатано в ( Borwein et al. 2008 ).
• Вейль, Андре (1948), Об алгебраических кривых и многообразиях, которые выводятся из них , Actualités Sci. Индиана, нет. 1041 = Опубл. Инст. Математика. унив. Страсбург 7 (1945), Hermann et Cie., Париж, MR   0027151
• Вейль, Андре (1949), «Числа решений уравнений в конечных полях», Бюллетень Американского математического общества , 55 (5): 497–508, doi : 10.1090/S0002-9904-1949-09219-4 , MR   0029393 Перепечатано в Oeuvres Scientifiques/Сборнике статей Андре Вейля. ISBN   0-387-90330-5
• Вайнбергер, Питер Дж. (1973), «О евклидовых кольцах целых алгебраических чисел», Аналитическая теория чисел (Университет Сент-Луиса, 1972) , Proc. Симпозиумы. Чистая математика., вып. 24, Провиденс, Род-Айленд: Амер. Математика. Соц., стр. 321–332, МР   0337902.
• Уайлс, Эндрю (2000), «Двадцать лет теории чисел», Математика: границы и перспективы , Провиденс, Род-Айленд: Американское математическое общество, стр. 329–342, ISBN  978-0-8218-2697-3 , МР   1754786
• Загер, Дон (1977), «Первые 50 миллионов простых чисел» (PDF) , Math. Intelligencer , 1 , Springer: 7–19, doi : 10.1007/BF03039306 , MR   0643810 , S2CID   189886510 , заархивировано из оригинала (PDF) 27 марта 2009 г.
• Загер, Дон (1981), «Ряды Эйзенштейна и дзета-функция Римана», Автоморфные формы, теория представлений и арифметика (Бомбей, 1979) , Tata Inst. Фонд. Рез. Исследования по математике, вып. 10, Тата Инт. Fundamental Res., Бомбей, стр. 275–301, MR   0633666.

Популярные экспозиции

• Саббаг, Карл (2003a), Величайшая нерешенная проблема математики , Фаррар, Штраус и Жиру, Нью-Йорк, ISBN  978-0-374-25007-2 , г-н   1979664
• Саббаг, Карл (2003b), нули доктора Римана , Atlantic Books, Лондон, ISBN  978-1-843-54101-1
• дю Сотуа, Маркус (2003), Музыка простых чисел , HarperCollins Publishers, ISBN  978-0-06-621070-4 , МР   2060134
• Рокмор, Дэн (2005), В поисках гипотезы Римана , Pantheon Books, ISBN  978-0-375-42136-5 , МР   2269393
• Дербишир, Джон (2003), Prime Obsession , Джозеф Генри Пресс, Вашингтон, округ Колумбия, ISBN  978-0-309-08549-6 , МР   : 1968857
• Уоткинс, Мэтью (2015), Тайна простых чисел , Liberalis Books, ISBN  978-1782797814 , МР   0000000
• Френкель, Эдвард (2014), гипотезе Римана Числофил по , 11 марта 2014 г. (видео)
• Нахин, Пол Дж . (2021). В погоне за Зетой-3: самая загадочная нерешенная математическая задача в мире . Издательство Принстонского университета. ISBN  978-0691206073 .

Примечание. Derbyshire 2003, Rockmore 2005, Sabbagh 2003a, Sabbagh 2003b, Sautoy 2003 и Watkins 2015 не являются техническими. Эдвардс 1974, Паттерсон 1988, Борвейн/Чой/Руни/Вейратмюллер 2008, Мазур/Штайн 2015, Броган 2017 и Нахин 2021 дают математические введения. Титчмарш 1986, Ивич 1985 и Карацуба/Воронин 1992 являются передовыми монографиями .

Внешние ссылки

• СМИ, связанные с гипотезой Римана, на Викискладе?

• Американский институт математики , гипотеза Римана
• База данных нулей , 103 800 788 359 нулей
• Апостол, Том , Где нули дзета с? Поэма о гипотезе Римана исполнении в Джона Дербишира .
• Борвейн, Питер , Гипотеза Римана (PDF) , заархивировано из оригинала (PDF) 27 марта 2009 г. (Слайды к лекции)
• Конрад, К. (2010), Последствия гипотезы Римана
• Конри, Дж. Брайан; Фармер, Дэвид В., Эквиваленты гипотезы Римана , заархивировано из оригинала 16 марта 2010 г.
• Гурдон, Ксавье; Себах, Паскаль (2004), Вычисление нулей дзета-функции (рассматривает гипотезу GUE, а также предоставляет обширную библиографию).
• Одлизко, Эндрю , Домашняя страница , включая статьи о нулях дзета-функции и таблицы нулей дзета-функции.
• Одлизко, Эндрю (2002), Нули дзета-функции Римана: гипотезы и вычисления (PDF) Слайды доклада
• Пегг, Эд (2004), Десять триллионов Зета-нулей , веб-сайт Math Games, заархивировано из оригинала 2 ноября 2004 г. , получено 20 октября 2004 г. Обсуждение расчета Ксавье Гурдоном первых десяти триллионов нетривиальных нулей.
• Рубинштейн, Майкл, Алгоритм генерации нулей , заархивировано из оригинала 27 апреля 2007 г.
• дю Сотуа, Маркус (2006), Prime Numbers Get Hitched , Seed Magazine, заархивировано из оригинала 22 сентября 2017 г. , получено 27 марта 2006 г. {{citation}}: CS1 maint: неподходящий URL ( ссылка )
• Уоткинс, Мэтью Р. (27 февраля 2021 г.), Предлагаемые (опровержения) доказательства гипотезы Римана , заархивировано из оригинала 9 декабря 2022 г.
• Zetagrid (2002) Проект распределенных вычислений, пытавшийся опровергнуть гипотезу Римана; закрыт в ноябре 2005 г.