Восьмая проблема Гильберта
Восьмая проблема Гильберта — одна из Дэвида Гильберта , списков открытых математических задач поставленных в 1900 году. Она касается теории чисел и, в частности, гипотезы Римана . [ 1 ] хотя это также связано с гипотезой Гольдбаха . Это требует дополнительной работы над распределением простых чисел и обобщением гипотезы Римана на другие кольца , где простые идеалы заменяют простые числа.
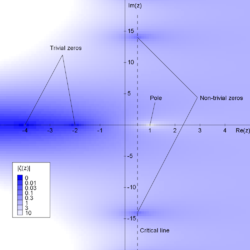
Гипотеза Римана и обобщения
[ редактировать ]Гильберт призывает к решению гипотезы Римана, которая долгое время считалась глубочайшей открытой проблемой математики. Учитывая решение, [ 2 ] он призывает к более тщательному исследованию дзета-функции Римана и теоремы о простых числах .
Гипотеза Гольдбаха
[ редактировать ]Гильберт призывает к решению гипотезы Гольдбаха, а также к более общим проблемам, таким как поиск бесконечного числа пар простых чисел, решающих фиксированное линейное диофантово уравнение .
Обобщенная гипотеза Римана
[ редактировать ]Наконец, Гильберт призывает математиков обобщить идеи гипотезы Римана на подсчет простых идеалов в числовом поле.
Внешние ссылки
[ редактировать ]Ссылки
[ редактировать ]- Бомбьери, Энрико (2006), «Гипотеза Римана» , Проблемы премии тысячелетия , Математический институт Клэя, Кембридж, Массачусетс: 107–124
- Моксли, Фредерик (2021), «Полные решения обратных квантовых классов ортогональной эквивалентности», Примеры и контрпримеры , 1 : 100003, doi : 10.1016/j.exco.2021.100003