Четвертая проблема Гильберта

В математике в четвертая проблема Гильберта списке проблем Гильберта 1900 года является фундаментальным вопросом геометрии . В одном утверждении, полученном из оригинала, речь шла о том, чтобы найти — с точностью до изоморфизма — все геометрии , которые имеют аксиоматическую систему классической геометрии ( евклидову , гиперболическую и эллиптическую ), с теми аксиомами сравнения , которые включают понятие опущенного угла. и добавлено « неравенство треугольника », рассматриваемое как аксиома.

Если принять дополнительно аксиому непрерывности, то в случае евклидовой плоскости мы придем к задаче, поставленной Жаном Гастоном Дарбу : «Чтобы определить все задачи вариационного исчисления на плоскости, решениями которых являются все плоские прямые линии ." ^{[ 1 ]}

Существует несколько интерпретаций оригинального высказывания Давида Гильберта . Тем не менее решение было найдено: немецкий математик Георг Гамель первым внес свой вклад в решение четвертой проблемы Гильберта. ^{[ 2 ]}

Признанное решение было дано советским математиком Алексеем Погореловым в 1973 году. ^{[ 3 ]}^{[ 4 ]} В 1976 году армянский математик Рубен В. Амбарцумян предложил еще одно доказательство четвертой проблемы Гильберта. ^{[ 5 ]}

Исходное заявление

Гильберт обсуждает существование неевклидовой геометрии и неархимедовой геометрии.

... геометрия, в которой выполняются все аксиомы обычной евклидовой геометрии, в частности все аксиомы сравнения, кроме аксиомы равенства треугольников (или все, кроме теоремы о равенстве основных углов в равнобедренном треугольнике), и в котором, кроме того, в качестве частной аксиомы принимается положение о том, что в каждом треугольнике сумма двух сторон больше третьей. ^{[ 6 ]}

В связи с идеей, что «прямая линия» определяется как кратчайший путь между двумя точками, он упоминает, что конгруэнтность треугольников необходима для доказательства Евклида, что прямая линия на плоскости — это кратчайшее расстояние между двумя точками. Он резюмирует следующее:

Теорема о прямой как кратчайшем расстоянии между двумя точками и эквивалентная по существу теорема Евклида о сторонах треугольника играют важную роль не только в теории чисел, но также в теории поверхностей и в вариационном исчислении. По этой причине, а также потому, что я считаю, что тщательное исследование условий справедливости этой теоремы прольет новый свет на идею расстояния, а также на другие элементарные идеи, например, на идею плоскости и возможность ее определения посредством идеи прямой линии, построение и систематическая обработка возможных здесь геометрий кажутся мне желательными. ^{[ 6 ]}

Плоские метрики

Теорема Дезарга :

Если два треугольника лежат на плоскости так, что линии, соединяющие соответствующие вершины треугольников, сходятся в одной точке, то три точки, в которых пересекаются продолжения трех пар соответствующих сторон треугольников, лежат на одной прямой.

Необходимым условием решения четвертой проблемы Гильберта является требование того, чтобы метрическое пространство, удовлетворяющее аксиомам этой проблемы, было дезарговым, т. е.:

если пространство имеет размерность 2, то должны выполняться теорема Дезарга и обратная к ней;
если пространство имеет размерность больше 2, то любые три точки должны лежать в одной плоскости.

Для дезарговых пространств Георг Гамель доказал, что каждое решение четвертой проблемы Гильберта может быть представлено в реальном проективном пространстве. $RP^{n}$ или в выпуклой области $RP^{n}$ если определить конгруэнтность отрезков равенством их длин в специальной метрике, для которой прямые проективного пространства являются геодезическими.

Метрики такого типа называются плоскими или проективными .

Таким образом, решение четвертой проблемы Гильберта свелось к решению проблемы конструктивного определения всех полных плоских метрик.

Гамель решил эту задачу в предположении высокой регулярности метрики. ^{[ 2 ]} Однако, как показывают простые примеры, класс регулярных плоских метрик меньше класса всех плоских метрик. Из аксиом рассматриваемых геометрий следует лишь непрерывность метрики. Поэтому для полного решения четвертой проблемы Гильберта необходимо конструктивно определить все непрерывные плоские метрики.

Предыстория четвертой проблемы Гильберта

До 1900 г. была известна модель Кэли-Клейна геометрии Лобачевского в единичном круге, согласно которой геодезические линии являются хордами диска, а расстояние между точками определяется как логарифм двойного отношения четверки. Для двумерных римановых метрик Эудженио Бельтрами (1835–1900) доказал, что плоские метрики являются метриками постоянной кривизны. ^{[ 7 ]}

Для многомерных римановых метрик это утверждение было доказано Э. Картаном в 1930 г.

В 1890 году для решения задач по теории чисел Герман Минковский ввёл понятие пространства, которое сейчас называется конечномерным банаховым пространством . ^{[ 8 ]}

Пространство Минковского

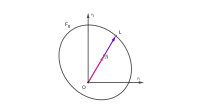
Позволять $F_{0}\subset \mathbb {E} ^{n}$ — компактная выпуклая гиперповерхность в евклидовом пространстве, определяемая формулой

F_{0}=\{y\in E^{n}:F(y)=1\},

где функция $F=F(y)$ удовлетворяет следующим условиям:

$F(y)\geqslant 0,\qquad F(y)=0\Leftrightarrow y=0;$
$F(\lambda y)=\lambda F(y),\qquad \lambda \geqslant 0;$
$F(y)\in C^{k}(E^{n}\setminus \{0\}),\qquad k\geqslant 3;$
и форма ${\frac {\partial ^{2}F^{2}}{\partial y^{i}\,\partial y^{j}}}\xi ^{i}\xi ^{j}>0$ является положительно определенным.

Длина вектора OA определяется:

\|OA\|_{M}={\frac {\|OA\|_{\mathbb {E} }}{\|OL\|_{\mathbb {E} }}}.

Пространство с такой метрикой называется пространством Минковского .

Гиперповерхность $F_{0}$ выпуклая и может быть неправильной. Определенная метрика является плоской.

Финслеровы пространства

Пусть М и $TM=\{(x,y)|x\in M,y\in T_{x}M\}$ — гладкое конечномерное многообразие и его касательное расслоение соответственно. Функция $F(x,y)\colon TM\rightarrow [0,+\infty )$ называется финслеровой метрикой, если

$F(x,y)\in C^{k}(TM\setminus \{0\}),\qquad k\geqslant 3$ ;
Для любой точки $x\in M$ ограничение $F(x,y)$ на $T_{x}M$ является нормой Минковского.

$(M,F)$ есть финслерово пространство .

геометрия Гильберта

Позволять $U\subset (\mathbb {E} ^{n+1},\|\cdot \|_{\mathbb {E} })$ — ограниченное открытое выпуклое множество с границей класса C ² и положительные нормальные кривизны. Как и в пространстве Лобачевского, гиперповерхность $\partial U$ называется абсолютом геометрии Гильберта. ^{[ 9 ]}

Расстояние Гильберта (см. рис.) определяется выражением

d_{U}(p,q)={\frac {1}{2}}\ln {\frac {\|q-q_{1}\|_{E}}{\|q-p_{1}\|_{E}}}\times {\frac {\|p-p_{1}\|_{E}}{\|p-q_{1}\|_{E}}}.

Расстояние $d_{U}$ индуцирует метрику Гильберта – Финслера $F_{U}$ на У. Для любого $x\in U$ и $y\in T_{x}U$ (см. рис.), имеем

F_{U}(x,y)={\frac {1}{2}}\|y\|_{\mathbb {E} }\left({\frac {1}{\|x-x_{+}\|_{\mathbb {E} }}}+{\frac {1}{\|x-x_{-}\|_{\mathbb {E} }}}\right).

Метрика симметричная и плоская. В 1895 году Гильберт представил эту метрику как обобщение геометрии Лобачевского. Если гиперповерхность $\partial U$ — эллипсоид, то мы имеем геометрию Лобачевского.

Фанк-метрика

В 1930 году Функ ввёл несимметричную метрику. Она определена в области, ограниченной замкнутой выпуклой гиперповерхностью, и также является плоской.

σ -метрика

Достаточное условие для плоских метрик

Георг Гамель был первым, кто внес свой вклад в решение четвертой проблемы Гильберта. ^{[ 2 ]} Он доказал следующее утверждение.

Теорема . Обычная метрика Финслера $F(x,y)=F(x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{n})$ является плоским тогда и только тогда, когда оно удовлетворяет условиям:

{\frac {\partial ^{2}F^{2}}{\partial x^{i}\,\partial y^{j}}}={\frac {\partial ^{2}F^{2}}{\partial x^{j}\,\partial y^{i}}},\,i,j=1,\ldots ,n.

Формула Крофтона

Рассмотрим набор всех ориентированных прямых на плоскости. Каждая строка определяется параметрами $\rho$ и $\varphi ,$ где $\rho$ - расстояние от начала координат до линии, а $\varphi$ представляет собой угол между линией и осью x . Тогда множество всех ориентированных прямых гомеоморфно круговому цилиндру радиуса 1 с элементом площади $dS=d\rho \,d\varphi$ . Позволять $\gamma$ быть спрямляемой кривой на плоскости. Тогда длина $\gamma$ является $L={\frac {1}{4}}\iint _{\Omega }n(\rho ,\varphi )\,dp\,d\varphi$ где $\Omega$ представляет собой набор линий, пересекающих кривую $\gamma$ , и $n(p,\varphi )$ - количество пересечений прямой с $\gamma$ . Крофтон доказал это утверждение в 1870 году. ^{[ 10 ]}

Аналогичное утверждение справедливо и для проективного пространства.

Мера Бляшке – Буземана

В 1966 году в своем выступлении на Международном математическом конгрессе в Москве Герберт Буземан представил новый класс плоских метрик. О множестве прямых на проективной плоскости $RP^{2}$ он ввел вполне аддитивную неотрицательную меру $\sigma$ , который удовлетворяет следующим условиям:

$\sigma (\tau P)=0$ , где $\tau P$ — набор прямых, проходящих через точку P ;
$\sigma (\tau X)>0$ , где $\tau X$ — множество прямых, проходящих через некоторое множество X , содержащее отрезок прямой;
$\sigma (RP^{n})$ конечно.

Если мы рассмотрим $\sigma$ -метрика в произвольной выпуклой области $\Omega$ проективного пространства $RP^{2}$ , то условие 3) следует заменить следующим: для любого множества H такого, что H содержится в $\Omega$ и замыкание H не пересекает границу $\Omega$ , неравенство

\sigma (\pi H)<\infty

держит. ^{[ 11 ]}

Используя эту меру, $\sigma$ -метрика включена $RP^{2}$ определяется

|x,y|=\sigma \left(\tau [x,y]\right),

где $\tau [x,y]$ это набор прямых, пересекающих отрезок $[x,y]$ .

Неравенство треугольника для этой метрики следует из теоремы Паша .

Теорема . $\sigma$ -метрика включена $RP^{2}$ является плоским, т. е. геодезическими являются прямые линии проективного пространства.

Но Буземан был далек от мысли, что $\sigma$ -метрики исчерпывают все плоские метрики. Он писал: «Свобода в выборе метрики с заданными геодезическими для неримановых метрик настолько велика, что можно усомниться в том, существует ли действительно убедительная характеристика всех дезарговых пространств» . ^{[ 11 ]}

Двумерный случай

Теорема Погорелова

Следующая теорема была доказана Погореловым в 1973 году. ^{[ 3 ]}^{[ 4 ]}

Теорема . Любая двумерная непрерывная полная плоская метрика является $\sigma$ -метрика.

Таким образом, четвертая проблема Гильберта для двумерного случая была полностью решена.

Следствием этого является то, что вы можете склеить границу с границей двух копий одной и той же плоской выпуклой формы, скрутив угол между ними, вы получите 3D-объект без линий сгиба, причем две грани могут быть развернуты .

Доказательства Амбарцумяна

В 1976 году Амбарцумян предложил еще одно доказательство четвертой проблемы Гильберта. ^{[ 5 ]}

Его доказательство использует тот факт, что в двумерном случае вся мера может быть восстановлена по ее значениям на двуугольниках и, таким образом, определена на треугольниках так же, как площадь треугольника определяется на сфере. Поскольку неравенство треугольника выполнено, то эта мера положительна на невырожденных треугольниках и определена на всех борелевских множествах . Однако эту структуру нельзя обобщить на более высокие измерения из-за третьей проблемы Гильберта, решенной Максом Деном .

В двумерном случае многоугольники одинакового объема равны ножницам. Как показал Ден, это неверно для более высокого измерения.

Трехмерный случай

Для трехмерного случая Погорелов доказал следующую теорему.

Теорема. Любая трехмерная регулярная полная плоская метрика является $\sigma$ -метрика.

Однако в трехмерном случае $\sigma$ -меры могут принимать как положительные, так и отрицательные значения. Необходимые и достаточные условия регулярной метрики, определяемой функцией множества $\sigma$ Чтобы быть плоским, необходимы следующие три условия:

ценность $\sigma$ в любой плоскости равен нулю,
ценность $\sigma$ в любом конусе неотрицательна,
ценность $\sigma$ положительно, если конус содержит внутренние точки.

Более того, Погорелов показал, что любая полная непрерывная плоская метрика в трехмерном случае является пределом регулярной $\sigma$ -метрики с равномерной сходимостью на любой компактной подобласти области определения метрики. Он назвал их обобщенными $\sigma$ -метрики.

Таким образом, Погорелов смог доказать следующее утверждение.

Теорема. В трехмерном случае любая полная непрерывная плоская метрика является $\sigma$ -метрика в обобщенном смысле.

Буземан в рецензии на книгу Погорелова «Четвертая проблема Гильберта» писал: «В духе того времени Гильберт ограничился n = 2, 3, и Погорелов тоже. Однако это имеет несомненные педагогические причины, поскольку он адресован широкому классу читателей. Реальная разница между n = 2 и n >2. Метод Погорелова работает при n >3, но требует большей технической подготовки». ^{[ 12 ]}

Многомерный случай

Многомерный случай четвертой проблемы Гильберта изучал Сабо. ^{[ 13 ]} В 1986 году он доказал, как и писал, обобщенную теорему Погорелова.

Теорема. Каждое n -мерное дезаргово пространство класса $C^{n+2},n>2$ , порождается конструкцией Бляшке–Буземана.

А $\sigma$ -мера, порождающая плоскую меру, обладает следующими свойствами:

тот $\sigma$ -мера гиперплоскостей, проходящих через неподвижную точку, равна нулю;
тот $\sigma$ -мера множества гиперплоскостей, пересекающих два отрезка [ x , y ], [ y , z ], где x , y та z не лежат на одной прямой, положительна.

Приведен пример плоской метрики, не порожденной конструкцией Бляшке–Буземана. Сабо описал все непрерывные плоские метрики в терминах обобщенных функций.

Четвертая проблема Гильберта и выпуклые тела

Четвертая проблема Гильберта также тесно связана со свойствами выпуклых тел . Выпуклый многогранник называется зонотопом, если он представляет собой Минковского сумму отрезков . Выпуклое тело, являющееся пределом зонотопов в метрике Бляшке – Хаусдорфа, называется зоноидом . Для зоноидов опорная функция представлена выражением

h(x)=\int _{S^{n-1}}\left|\left\langle x,u\right\rangle \right|\partial \sigma (u),

( 1 )

где $\sigma (u)$ является четной положительной борелевской мерой на сфере $S^{n-1}$ .

Пространство Минковского порождается конструкцией Бляшке–Буземана тогда и только тогда, когда опорная функция индикатрисы имеет вид (1), где $\sigma (u)$ четна и не обязательно имеет положительную борелевскую меру. ^{[ 14 ]} Тела, ограниченные такими гиперповерхностями, называются обобщенными зоноидами .

Октаэдр $|x_{1}|+|x_{2}|+|x_{3}|\leq 1$ в евклидовом пространстве $E^{3}$ не является генерализованным зоноидом. Из приведенного утверждения следует, что плоская метрика пространства Минковского с нормой $\|x\|=\max\{|x_{1}|,|x_{2}|,|x_{3}|\}$ не порождается конструкцией Бляшке–Буземана.

Обобщения четвертой проблемы Гильберта.

Найдено соответствие между плоскими n -мерными финслеровыми метриками и специальными симплектическими формами на многообразии Грассмана. $G(n+1,2)$ в $E^{n+1}$ . ^{[ 15 ]}

Рассмотрены периодические решения четвертой проблемы Гильберта:

Пусть ( M , g ) — компактное локально евклидово риманово многообразие. Предположим, что $C^{2}$ финслерова метрика на M с теми же геодезическими, что и в метрике g Дана . Тогда финслерова метрика является суммой локальной метрики Минковского и замкнутой 1-формы. ^{[ 16 ]}
Пусть ( M , g ) — компактное симметрическое риманово пространство ранга больше единицы. Если F — симметричный $C^{2}$ финслеровой метрики, геодезические которой совпадают с геодезическими римановой метрики g , то ( M , g ) — симметричное финслерово пространство. ^{[ 16 ]} Аналог этой теоремы для симметрических пространств ранга один пока не доказан.

Другое изложение четвертой проблемы Гильберта можно найти в работе Пайвы. ^{[ 17 ]}

Нерешенные проблемы

Четвертая проблема Гильберта для несимметричной финслеровой метрики до сих пор не решена.
Описание метрики на $RP^{n}$ для которых k -плоскости минимизируют k -площадь, не дано (Буземанн). ^{[ 18 ]}

Ссылки

^ Дарбу, Гастон (1894). Уроки по общей теории поверхностей . Полет. III. Париж. {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Jump up to: ^а ^б ^с Хамель, Георг (1903). «О геометриях, в которых прямые являются кратчайшими» . Математические летописи . 57 (2): 221–264. дои : 10.1007/BF01444348 .
^ Jump up to: ^а ^б А. В. Погорелов, Полное решение IV проблемы Гильберта , ДАН СССР № 208, т.1 (1973), 46–49. English translation: Pogorelov, A. V. (1973). "A complete solution of Hilbert's fourth problem ". Doklady Akademii Nauk SSSR . 208 (1): 48–52.
^ Jump up to: ^а ^б А. В. Погорелов, Четвертая Проблема Гильберта . Наука, 1974. English translation: A.V. Pogorelov, Hilbert's Fourth Problem , Scripta Series in Mathematics, Winston and Sons, 1979.
^ Jump up to: ^а ^б Р. В. Амбарцумян, Заметка о псевдометриках на плоскости, Журнал теории вероятностей и смежных областей. 1976, том 37, выпуск 2, стр. 145–155.
^ Jump up to: ^а ^б Гильберт, Дэвид, «Математические проблемы» Göttinger Nachrichten , (1900), стр. 253–297, и в «Архиве математики и физики» , (3) 1 (1901), 44–63 и 213–237. Опубликовано в английском переводе Dr. Мэби Уинтон Ньюсон, Гильберт, Дэвид (1902). «Математические задачи» . Бюллетень Американского математического общества . 8 (10): 437–479. дои : 10.1090/S0002-9904-1902-00923-3 . . [Более полное название журнала Göttinger Nachrichten — Nachrichten von der Königl. Общество науки в Геттинген.]
^ Бельтрами, Эудженио (1865). «Решение задач: нанесение точек поверхности над плоскостью так, чтобы геодезические линии были представлены прямыми линиями» . Анналы чистой и прикладной математики . 7 : 185–204. дои : 10.1007/BF03198517 . S2CID 123192933 .
^ Минковский, Герман (1953). Геометрия чисел . Б. Г. Тойбнер, Лейпциг-Берлин.
^ Гильберт, Дэвид (1895). «О прямой, как кратчайшем соединении двух точек» . Математические летописи . 46 :91-96. дои : 10.1007/BF02096204 .
^ Сантало, Луис А. (1967). «Интегральная геометрия». В Черне С.С. (ред.). Исследования в области глобальной геометрии и анализа . Математическая ассоциация Америки, Вашингтон, округ Колумбия, стр. 147–195.
^ Jump up to: ^а ^б Буземанн, Герберт (1955). Геометрия геодезических . Академик Пресс, Нью-Йорк.
^ Буземанн, Герберт (1981). "Рецензия на: А.В. Погорелов, Четвертая проблема Гильберта" . Бюллетень Американского математического общества . Новая серия. 4 (1): 87–90. дои : 10.1090/S0273-0979-1981-14867-9 .
^ Сабо, З.И. (1986). «Четвертая проблема Гильберта I» . Достижения в математике . 59 (3): 185–301. дои : 10.1016/0001-8708(86)90056-3 .
^ Александр, Ральф (1988). «Теория Зоноида и четвертая проблема Гильберта». Геометрии посвященные . 28 (2): 199–211. дои : 10.1007/BF00147451 . S2CID 119391326 .
^ Альварес Пайва, JC (2005). «Симплетическая геометрия и четвертая проблема Гильберта» . Журнал дифференциальной геометрии . 69 (2): 353–378. дои : 10.4310/jdg/1121449109 .
^ Jump up to: ^а ^б Альварес Пайва, JC; Барбоса Гомес, Дж. (2018). «Периодические решения четвертой проблемы Гильберта». Журнал топологии и анализа . arXiv : 1809.02783 . дои : 10.1142/S1793525321500576 . S2CID 240026741 .
^ Альварес Пайва, JC (2003). «Четвертая проблема Гильберта в двух измерениях». МАССА Selecta : 165–183.
^ Пападопулос, Атанас (2014). «Четвертая проблема Гильберта» . У Пападопулоса — Афанасий; Троянов, Марк (ред.). Справочник по геометрии Гильберта . Лекции ИРМА по математике и теоретической физике. Том. 22. Европейское математическое общество. стр. 391–431. дои : 10.4171/147-1/15 . ISBN 978-3-03719-147-7 .

Дальнейшее чтение

Буземанн, Герберт (1976). «Проблема IV. Дезарговы пространства». В Браудер, Феликс Э. (ред.). Математические разработки, вытекающие из задач Гильберта . Труды симпозиумов по чистой математике . Том. ХXVIII. Американское математическое общество . стр. 131–141. ISBN 0-8218-1428-1 . Збл 0352.50010 .
Пападопулос, Атанас (2014). «Четвертая проблема Гильберта». Справочник по геометрии Гильберта (А. Пападопулос и М. Троянов, ред.) . Лекции ИРМА по математике и теоретической физике . Том. 22. Европейское математическое общество . стр. 391–432. ISBN 978-3-03719-147-7 .

[1] Дарбу, Гастон (1894). Уроки по общей теории поверхностей . Полет. III. Париж. {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[Hamel1903-2] Jump up to: ^а ^б ^с Хамель, Георг (1903). «О геометриях, в которых прямые являются кратчайшими» . Математические летописи . 57 (2): 221–264. дои : 10.1007/BF01444348 .

[Pogorelov1973-3] Jump up to: ^а ^б А. В. Погорелов, Полное решение IV проблемы Гильберта , ДАН СССР № 208, т.1 (1973), 46–49. English translation: Pogorelov, A. V. (1973). "A complete solution of Hilbert's fourth problem ". Doklady Akademii Nauk SSSR . 208 (1): 48–52.

[Pogorelov1974-4] Jump up to: ^а ^б А. В. Погорелов, Четвертая Проблема Гильберта . Наука, 1974. English translation: A.V. Pogorelov, Hilbert's Fourth Problem , Scripta Series in Mathematics, Winston and Sons, 1979.

[Ambartzumian1976-5] Jump up to: ^а ^б Р. В. Амбарцумян, Заметка о псевдометриках на плоскости, Журнал теории вероятностей и смежных областей. 1976, том 37, выпуск 2, стр. 145–155.

[Hilbert1900-6] Jump up to: ^а ^б Гильберт, Дэвид, «Математические проблемы» Göttinger Nachrichten , (1900), стр. 253–297, и в «Архиве математики и физики» , (3) 1 (1901), 44–63 и 213–237. Опубликовано в английском переводе Dr. Мэби Уинтон Ньюсон, Гильберт, Дэвид (1902). «Математические задачи» . Бюллетень Американского математического общества . 8 (10): 437–479. дои : 10.1090/S0002-9904-1902-00923-3 . . [Более полное название журнала Göttinger Nachrichten — Nachrichten von der Königl. Общество науки в Геттинген.]

[7] Бельтрами, Эудженио (1865). «Решение задач: нанесение точек поверхности над плоскостью так, чтобы геодезические линии были представлены прямыми линиями» . Анналы чистой и прикладной математики . 7 : 185–204. дои : 10.1007/BF03198517 . S2CID 123192933 .

[8] Минковский, Герман (1953). Геометрия чисел . Б. Г. Тойбнер, Лейпциг-Берлин.

[9] Гильберт, Дэвид (1895). «О прямой, как кратчайшем соединении двух точек» . Математические летописи . 46 :91-96. дои : 10.1007/BF02096204 .

[10] Сантало, Луис А. (1967). «Интегральная геометрия». В Черне С.С. (ред.). Исследования в области глобальной геометрии и анализа . Математическая ассоциация Америки, Вашингтон, округ Колумбия, стр. 147–195.

[Buseman1955-11] Jump up to: ^а ^б Буземанн, Герберт (1955). Геометрия геодезических . Академик Пресс, Нью-Йорк.

[12] Буземанн, Герберт (1981). "Рецензия на: А.В. Погорелов, Четвертая проблема Гильберта" . Бюллетень Американского математического общества . Новая серия. 4 (1): 87–90. дои : 10.1090/S0273-0979-1981-14867-9 .

[13] Сабо, З.И. (1986). «Четвертая проблема Гильберта I» . Достижения в математике . 59 (3): 185–301. дои : 10.1016/0001-8708(86)90056-3 .

[14] Александр, Ральф (1988). «Теория Зоноида и четвертая проблема Гильберта». Геометрии посвященные . 28 (2): 199–211. дои : 10.1007/BF00147451 . S2CID 119391326 .

[15] Альварес Пайва, JC (2005). «Симплетическая геометрия и четвертая проблема Гильберта» . Журнал дифференциальной геометрии . 69 (2): 353–378. дои : 10.4310/jdg/1121449109 .

[Paiva2018-16] Jump up to: ^а ^б Альварес Пайва, JC; Барбоса Гомес, Дж. (2018). «Периодические решения четвертой проблемы Гильберта». Журнал топологии и анализа . arXiv : 1809.02783 . дои : 10.1142/S1793525321500576 . S2CID 240026741 .

[17] Альварес Пайва, JC (2003). «Четвертая проблема Гильберта в двух измерениях». МАССА Selecta : 165–183.

[Papadopoulos2004-18] Пападопулос, Атанас (2014). «Четвертая проблема Гильберта» . У Пападопулоса — Афанасий; Троянов, Марк (ред.). Справочник по геометрии Гильберта . Лекции ИРМА по математике и теоретической физике. Том. 22. Европейское математическое общество. стр. 391–431. дои : 10.4171/147-1/15 . ISBN 978-3-03719-147-7 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]