Гипотеза Гольдбаха

Гипотеза Гольдбаха
	Письмо Гольдбаха Эйлеру от 7 июня 1742 г. (латино-немецкий)
Поле	Теория чисел
Предполагается	Кристиан Гольдбах
Предполагается в	1742
Открытая проблема	Да
Последствия	Слабая гипотеза Гольдбаха

Гипотеза Гольдбаха — одна из старейших и самых известных нерешённых проблем теории чисел и всей математики . Он гласит, что каждое четное натуральное число больше 2 является суммой двух простых чисел .

Было показано, что гипотеза верна для всех целых чисел меньше 4 × 10. ¹⁸ но остается недоказанным, несмотря на значительные усилия.

История [ править ]

Происхождение [ править ]

7 июня 1742 года прусский математик Кристиан Гольдбах написал письмо Леонарду Эйлеру (письмо XLIII): ^[2] в котором он выдвинул следующую гипотезу:

что каждое число, состоящее из двух numeris primis, представляет собой совокупность любого числа numerorum primorum (включая единицу), за исключением congeriem omnium unitatum.
Каждое целое число, которое можно записать как сумму двух простых чисел, также можно записать как сумму любого количества простых чисел, пока все члены не станут единицами.

Гольдбах следовал ныне заброшенному соглашению считать 1 числом простым . ^[3] так что сумма единиц будет суммой простых чисел.Затем он выдвинул вторую гипотезу на полях своего письма, которая подразумевает первую: ^[4]

... каждое число больше 2 представляет собой совокупность trium numerorum primorum.
Каждое целое число больше 2 можно записать как сумму трёх простых чисел.

Эйлер ответил в письме от 30 июня 1742 г. ^[5] и напомнил Гольдбаху о их более раннем разговоре (« ... so Ew vormals mit mir communicirt haben... »), в котором Гольдбах заметил, что первое из этих двух предположений следует из утверждения

Каждое положительное четное целое число можно записать как сумму двух простых чисел.

Фактически это эквивалентно его второй, маргинальной гипотезе.В письме от 30 июня 1742 года Эйлер заявил: ^[6]^[7]

Я считаю, что... каждое число par a summa duorum primorum является весьма достоверной теоремой, хотя я не могу доказать то же самое.
То, что... всякое четное целое число есть сумма двух простых чисел, я считаю вполне достоверной теоремой, хотя доказать ее не могу.

Частичные результаты [ править ]

Сильная гипотеза Гольдбаха гораздо сложнее слабой гипотезы Гольдбаха . Используя метод Виноградова, Николай Чудаков , ^[8] Йоханнес ван дер Корпут , ^[9] и Теодор Эстерманн ^[10] показал, что почти все четные числа можно записать в виде суммы двух простых чисел (в том смысле, что доля четных чисел до некоторого $N$ , которую можно записать таким образом, стремится к 1 по мере $увеличения N$ ). В 1930 году Лев Шнирельман доказал, что любое натуральное число больше 1 можно записать как сумму не более чем $C$ простых чисел, где $C$ — эффективно вычислимая константа; см. плотность Шнирельмана . ^[11]^[12] Константа Шнирельмана — это наименьшее число $C$ с этим свойством. Сам Шнирельман получил $C < 800000$ . Этот результат впоследствии был усилен многими авторами, такими как Оливье Рамаре , который в 1995 году показал, что каждое четное число $n \geq 4$ на самом деле является суммой не более 6 простых чисел. Самый известный результат в настоящее время основан на доказательстве слабой гипотезы Гольдбаха Харальдом Хельфготтом : ^[13] из чего напрямую следует, что каждое четное число $n \geq 4$ представляет собой сумму не более 4 простых чисел. ^[14]^[15]

В 1924 году Харди и Литтлвуд в предположении обобщенной гипотезы Римана показали , что число четных чисел до $X,$ нарушающих гипотезу Гольдбаха, намного меньше $X. .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1 ⁄ 2 + с$ для маленького $c$ . ^[16]

В 1948 году, используя теории решета методы , Альфред Реньи показал, что каждое достаточно большое четное число можно записать в виде суммы простого и почти простого числа с не более чем $K$ множителями. ^[17] В 1973 году Чэнь Цзинжунь с помощью теории решета показал, что каждое достаточно большое четное число можно записать как сумму либо двух простых чисел, либо простого и полупростого числа (произведения двух простых чисел). ^[18] см. в теореме Чена Дополнительную информацию .

В 1975 году Хью Лоуэлл Монтгомери и Боб Вон показали, что «большинство» четных чисел выражаются как сумма двух простых чисел. Точнее, они показали, что существуют положительные константы $c$ и $C$ такие, что для всех достаточно больших чисел $N$ каждое четное число меньше $N$ является суммой двух простых чисел, причем не более $CN 1 - с$ исключения. В частности, множество четных целых чисел, не являющихся суммой двух простых чисел, имеет плотность нулевую .

В 1951 году Юрий Линник доказал существование константы $K$ такой, что каждое достаточно большое четное число представляет собой сумму двух простых чисел и не более $K$ степеней 2. Янош Пинц и Имре Ружа обнаружили в 2020 году, что $K = 8$ работает. ^[19] Если принять обобщенную гипотезу Римана , $K = 7$ также работает, как показали Роджер Хит-Браун и Ян-Кристоф Шлаге-Пухта в 2002 году. ^[20]

Доказательство слабой гипотезы было представлено в 2013 году Харальдом Хелфготтом в серии «Анналы математических исследований» . Хотя статья была принята, Хелфготт решил внести существенные изменения, предложенные рецензентом. Несмотря на несколько поправок, доказательство Хелфготта еще не появилось в рецензируемой публикации. ^[21]^[22]^[23] Слабая гипотеза вытекает из сильной гипотезы, как если бы $n - 3$ — сумма двух простых чисел, то $n$ — сумма трех простых чисел. Однако обратный вывод и, следовательно, сильная гипотеза Гольдбаха останутся недоказанными, если доказательство Хельфготта верно.

Результаты вычислений [ править ]

Для малых значений $n$ сильная гипотеза Гольдбаха (и, следовательно, слабая гипотеза Гольдбаха) может быть проверена непосредственно. Например, в 1938 году Нильс Пиппинг тщательно проверил гипотезу до $n = 100000$ . ^[24] С появлением компьютеров $гораздо больше значений n$ было проверено ; Т. Оливейра и Силва провел распределенный компьютерный поиск, который подтвердил гипотезу для $n \leq 4 \times 10. 18$ (и перепроверено до 4 × 10 ¹⁷) по состоянию на 2013 год. Одна из записей этого поиска гласит, что 3 325 581 707 333 960 528 — это наименьшее число, которое нельзя записать в виде суммы двух простых чисел, одно из которых меньше 9781. ^[25]

Калли-Хугилл и Дудек доказывают ^[26] (частичный и условный) результат по гипотезе Римана: существует сумма двух нечетных простых чисел в интервале (x, x + 9696 log^2 x] для всех x ≥ 2.

В популярной культуре [ править ]

Гипотеза Гольдбаха ( китайский : 哥德巴赫猜想 ) — это название биографии китайского математика и теоретика чисел Чэнь Цзинжуня , написанной Сюй Чи .

Эта гипотеза является центральным моментом в сюжете романа 1992 года « Дядя Петрос и гипотеза Гольдбаха» греческого писателя Апостолоса Доксиадиса , в рассказе « Шестьдесят миллионов триллионов комбинаций » Айзека Азимова , а также в детективном романе «Никто, кого вы не знаете » Мишель 2008 года. Ричмонд . ^[27]

Гипотеза Гольдбаха является частью сюжета испанского фильма 2007 года « Комната Ферма» .

Гипотеза Гольдбаха стала основной темой исследования героини актрисы Эллы Рампф Маргариты во французско-швейцарском фильме 2023 года «Теорема Маргариты» . ^[28]

Официальное заявление [ править ]

Каждая из трех гипотез имеет естественный аналог в современном определении простого числа, согласно которому единица исключается. Современная версия первой гипотезы такова:

Каждое целое число, которое можно записать как сумму двух простых чисел, можно также записать как сумму любого количества простых чисел, пока либо все члены не станут двумя (если целое число четное), либо один член не будет равен трем, а все остальные члены не станут равными двум. два (если целое число нечетное).

Современная версия маргинальной гипотезы такова:

Любое целое число больше 5 можно записать как сумму трёх простых чисел.

А современная версия старой гипотезы Гольдбаха, о которой ему напомнил Эйлер, такова:

Каждое четное целое число больше 2 можно записать как сумму двух простых чисел.

Эти современные версии могут быть не полностью эквивалентны соответствующим оригинальным утверждениям. Например, если бы существовало четное целое число $N = p + 1,$ большее 4, где $p —$ простое число, которое нельзя было бы выразить как сумму двух простых чисел в современном смысле слова, то это было бы контрпримером к современной версии формулы. третья гипотеза (не являющаяся контрпримером к исходной версии). Таким образом, современная версия, вероятно, сильнее (но чтобы подтвердить это, нужно было бы доказать, что первая версия, свободно применимая к любому положительному даже целому числу $n$ , не может исключить существование такого конкретного контрпримера $N$ ). В любом случае современные утверждения имеют те же отношения друг с другом, что и более старые утверждения. То есть второе и третье современные утверждения эквивалентны, и любое из них подразумевает первое современное утверждение.

Третье современное утверждение (эквивалентное второму) — это форма, в которой гипотеза обычно выражается сегодня. Она также известна как « сильная », «четная» или «бинарная» гипотеза Гольдбаха. Более слабая форма второго современного утверждения, известная как « слабая гипотеза Гольдбаха », «нечетная гипотеза Гольдбаха» или «троичная гипотеза Гольдбаха», утверждает, что

Каждое нечетное целое число больше 7 можно записать как сумму трех нечетных простых чисел.

Эвристическое обоснование [ править ]

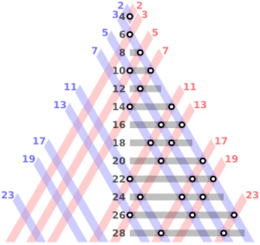
Статистические соображения, сосредоточенные на вероятностном распределении простых чисел, представляют неофициальные доказательства в пользу гипотезы (как в слабой, так и в сильной форме) для достаточно больших целых чисел: чем больше целое число, тем больше способов существует для представления этого числа. как сумма двух или трех других чисел, и тем более «вероятно» становится, что хотя бы одно из этих представлений полностью состоит из простых чисел.

Количество способов записать четное число $n$ в виде суммы двух простых чисел (последовательность A002375 в OEIS )

Очень грубая версия эвристического вероятностного аргумента (для сильной формы гипотезы Гольдбаха) состоит в следующем. Теорема о простых числах утверждает, что целое число $m,$ выбранное наугад, имеет примерно $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1 / ln m$ шанс быть простым. Таким образом, если $n$ — большое четное целое число, а $m$ — число от 3 до $n / 2$ , то можно было бы ожидать, что вероятность того, что $m$ и $n - m$ одновременно будут простыми, будет равна $1 / пер м пер(п - м)$ . Если следовать этой эвристике, можно было бы ожидать, что общее количество способов записать большое четное целое число $n$ в виде суммы двух нечетных простых чисел будет примерно равно

\sum _{m=3}^{\frac {n}{2}}{\frac {1}{\ln m}}{\frac {1}{\ln(n-m)}}\approx {\frac {n}{2(\ln n)^{2}}}.

Поскольку $ln n ≪ \sqrt n$ , эта величина стремится к бесконечности с $увеличением n$ , и можно было бы ожидать, что каждое большое четное целое число имеет не только одно представление в виде суммы двух простых чисел, но на самом деле очень много таких представлений.

Этот эвристический аргумент на самом деле несколько неточный, поскольку он предполагает, что события, когда $m$ и $n - m$ являются простыми, статистически независимы друг от друга. Например, если $m$ нечетно, то $n - m$ также нечетно, а если $m$ четно, то $n - m$ четно, что нетривиально, поскольку, кроме числа 2, простыми могут быть только нечетные числа. Аналогично, если $n$ делится на 3, а $m$ уже было простым числом, отличным от 3, то $n - m$ также будет взаимно простым с 3 и, таким образом, с немного большей вероятностью будет простым, чем общее число. Более тщательно проводя этот тип анализа, Г.Х. Харди и Джон Эденсор Литтлвуд в 1923 году предположили (в рамках своей гипотезы Харди-Литтлвуда о простых кортежах ), что для любого фиксированного $c \geq 2$ число представлений большого целого числа $n$ как сумма $c$ простые числа $n = p 1 + \dots + с pc$ p $1 \leq \dots \leq pc должны$ быть асимптотически равны

\left(\prod _{p}{\frac {p\gamma _{c,p}(n)}{(p-1)^{c}}}\right)\int _{2\leq x_{1}\leq \cdots \leq x_{c}:x_{1}+\cdots +x_{c}=n}{\frac {dx_{1}\cdots dx_{c-1}}{\ln x_{1}\cdots \ln x_{c}}},

где произведение рассчитано по всем простым числам $p$ , а $γ c, p (n)$ — количество решений уравнения $n = q 1 + \dots + q c mod p$ в модульной арифметике с учетом ограничений $q 1, \dots, q с \neq 0 мод п$ . Асимптотическая справедливость этой формулы для $c \geq 3$ была строго доказана в работе Ивана Матвеевича Виноградова , но остается лишь гипотезой при $c = 2$ . ^{[ нужна ссылка ]} В последнем случае приведенная выше формула упрощается до 0, когда $n$ нечетно, и до

2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right)\int _{2}^{n}{\frac {dx}{(\ln x)^{2}}}\approx 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right){\frac {n}{(\ln n)^{2}}}

когда $n$ четное, где $Π 2$ - постоянная простых чисел-близнецов Харди–Литтлвуда.

\Pi _{2}:=\prod _{p\;{\rm {prime}}\geq 3}\left(1-{\frac {1}{(p-1)^{2}}}\right)\approx 0.66016\,18158\,46869\,57392\,78121\,10014\dots

Иногда это называют расширенной гипотезой Гольдбаха . Сильная гипотеза Гольдбаха на самом деле очень похожа на гипотезу о простых числах-близнецах , и считается, что обе гипотезы имеют примерно сопоставимую сложность.

— Статистическая сумма Гольдбаха это функция, которая сопоставляет каждому четному целому числу способов его разложения в сумму двух простых чисел. Ее график похож на комету , поэтому ее называют кометой Гольдбаха . ^[29]

Комета Гольдбаха предполагает жесткие верхние и нижние границы количества представлений четного числа в виде суммы двух простых чисел, а также то, что количество этих представлений сильно зависит от значения числа по модулю 3.

Связанные проблемы [ править ]

Хотя гипотеза Гольдбаха подразумевает, что каждое положительное целое число, большее единицы, можно записать как сумму не более трех простых чисел, не всегда возможно найти такую сумму с помощью жадного алгоритма , который на каждом шаге использует максимально возможное простое число. Последовательность Пиллаи отслеживает числа, требующие наибольшего количества простых чисел в их жадных представлениях. ^[30]

Существуют проблемы, аналогичные гипотезе Гольдбаха, в которых простые числа заменяются другими конкретными наборами чисел, такими как квадраты:

доказал Лагранж , что каждое положительное целое число является суммой четырёх квадратов . См. проблему Уоринга и связанную с ней проблему Уоринга – Гольдбаха о суммах степеней простых чисел.
Харди и Литтлвуд перечислили свою гипотезу I: «Каждое большое нечетное число ( $n > 5$ ) представляет собой сумму простого и двойного простого числа». ^[31] Эта гипотеза известна как гипотеза Лемуана , а также гипотеза Леви .
Гипотеза Гольдбаха о практических числах — последовательности целых чисел, подобной простым числам, — была сформулирована Маргенштерном в 1984 году: ^[32] и доказано Мелфи в 1996 году: ^[33] каждое четное число представляет собой сумму двух практических чисел.
Харви Дубнер предложил усилить гипотезу Гольдбаха, согласно которой каждое четное целое число больше 4208 представляет собой сумму двух простых чисел-близнецов (не обязательно принадлежащих одной и той же паре). ^[34]^{[ нужен лучший источник ]} Только 34 четных целых числа меньше 4208 не являются суммой двух простых чисел-близнецов; Дубнер вычислительно подтвердил, что этот список полон до $2\cdot 10^{10}.$ ^[35]^{[ нужна проверка ]} Доказательство этой более сильной гипотезы подразумевало бы не только гипотезу Гольдбаха, но и гипотезу простых чисел-близнецов .

Ссылки [ править ]

^ Математическое и физическое соответствие некоторых известных геометров XVIII века (Группа 1), СПб. 1843, стр. 125–129 .
^ http://www.math.dartmouth.edu/~euler/correspondence/letters/OO0765.pdf ^{[ пустой URL PDF ]}
^ Вайсштейн, Эрик В. «Гипотеза Гольдбаха» . Математический мир .
^ В печатной версии, опубликованной PH Fuss [1] в маргинальной гипотезе 2 ошибочно напечатано как 1.
^ http://eulerarchive.maa.org//correspondence/letters/OO0766.pdf. ^{[ пустой URL PDF ]}
^ Ингэм, А.Е. «Популярные лекции» (PDF) . Архивировано из оригинала (PDF) 16 июня 2003 г. Проверено 23 сентября 2009 г.
^ Колдуэлл, Крис (2008). «Гипотеза Гольдбаха» . Проверено 13 августа 2008 г.
^ Чудаков, Николаи Г. (1937). " О проблеме Гольдбаха" [ On the Goldbach problem ]. Doklady Akademii Nauk SSSR . 17 : 335-338.
^ Ван дер Корпут, JG (1938). «О гипотезе Гольдбаха» (PDF) . Учеб. Акад. Влажный. Амстердам (на французском языке). 41 :76–80.
^ Эстерманн, Т. (1938). «О проблеме Гольдбаха: доказательство того, что почти все четные положительные целые числа являются суммами двух простых чисел». Учеб. Лондонская математика. Соц . 2. 44 : 307–314. дои : 10.1112/plms/s2-44.4.307 .
^ Шнирельманн, LG (1930). « Об аддитивных свойствах чисел », впервые опубликовано в «Записках Донского политехнического института в Новочеркасске» (на русском языке), т. 14 (1930), с. 3–27, и перепечатано в «Успехах математических наук» (на русском языке). ), 1939, вып. 6, 9–25.
^ Шнирельманн, Л.Г. (1933). Впервые опубликовано под названием « Об аддитивных свойствах чисел » в « Mathematische Annalen » (на немецком языке), том. 107 (1933), 649–690 и перепечатано как « Об аддитивных свойствах чисел » в «Успехах математических наук», 1940, вып. 7, 7–46.
^ Хелфготт, ХА (2013). «Тройная гипотеза Гольдбаха верна». arXiv : 1312.7748 [ math.NT ].
^ Синисало, Матти К. (октябрь 1993 г.). «Проверка гипотезы Гольдбаха до 4 ⋅ 10 ¹¹ Математика (PDF) . вычислений . 61 (204). Американское математическое общество: 931–934. CiteSeerX 10.1.1.364.3111 . doi : 10.2307/2153264 . JSTOR 2153264 .
^ Рассиас, М.Т. (2017). Проблема Гольдбаха: избранные темы . Спрингер.
^ См., например, « Новую явную формулу аддитивной теории простых чисел с приложениями I. Явную формулу для задач Гольдбаха и обобщенных проблем простых чисел-близнецов» Яноша Пинца.
^ Реньи, А.А. (1948). «О представлении четного числа в виде суммы простого и почти простого». Известия Академии Наук СССР Серия Математическая (на русском языке). 12 : 57–78.
^ Чен, младший (1973). «О представлении большего четного целого числа в виде суммы простого числа и произведения не более двух простых чисел». наук. Синица . 16 : 157–176.
^ Пинц, Дж .; Ружа, ИЗ (01.08.2020). «О приближении Линника к задаче Гольдбаха. II» . Acta Mathematica Hungarica . 161 (2): 569–582. дои : 10.1007/s10474-020-01077-8 . ISSN 1588-2632 . S2CID 54613256 .
^ Хит-Браун, ДР; Пухта, Дж. К. (2002). «Целые числа представлены как сумма простых чисел и степеней двойки». Азиатский математический журнал . 6 (3): 535–565. arXiv : math.NT/0201299 . Бибкод : 2002math......1299H . дои : 10.4310/AJM.2002.v6.n3.a7 . S2CID 2843509 .
^ Хелфготт, ХА (2013). «Основные дуги теоремы Гольдбаха». arXiv : 1305.2897 [ math.NT ].
^ Хелфготт, ХА (2012). «Второстепенные дуги проблемы Гольдбаха». arXiv : 1205.5252 [ math.NT ].
^ «Харальд Андрес Хелфготт» . Институт математики Жюсье-Париж Рив Гош . Проверено 06 апреля 2021 г.
^ Пиппинг, Нильс (1890–1982), «Гипотеза Гольдбаха и теорема Гольдбаха-Виноградова». Акта Акад. Абоэнсис, Матем. 11, 4–25, 1938.
^ Томас Оливейра и Силва, Проверка гипотезы Гольдбаха . Проверено 20 апреля 2024 г.
^ Микаэла Калли-Хугилл и Адриан В. Дудек, Явная оценка среднего значения для PNT в интервалах
^ «Математическая фантастика: ты никого не знаешь (Мишель Ричмонд)» . kasmana.people.cofc.edu .
^ Одиль Морен Теорема Маргариты , в ФранцияИнформация:культура
^ Флигель, Генри Ф.; Робертсон, Дуглас С. (1989). «Комета Гольдбаха: числа, связанные с гипотезой Гольдбаха». Журнал развлекательной математики . 21 (1): 1–7.
^ Слоан, Нью-Джерси (ред.). «Последовательность A066352 (последовательность Пиллаи)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.
^ Журнал Mathematics , 66:1 (1993): 45–47.
^ Маргенштерн, М. (1984). «Результаты и предположения о практических числах». Известия Академии наук . 299 : 895–898.
^ Мелфи, Г. (1996). «О двух предположениях о практических числах» . Журнал теории чисел . 56 : 205–210. дои : 10.1006/jnth.1996.0012 .
^ «Гипотезы ПРАЙМ-БЛИЗНЕЦ» (PDF) . oeis.org .
^ Слоан, Нью-Джерси (ред.). «Последовательность A007534 (Четные числа, не являющиеся суммой пары простых чисел-близнецов)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.

Дальнейшее чтение [ править ]

Дешуйе, Ж.-М.; Эффингер, Г.; те Риле, Х.; Зиновьев, Д. (1997). «Полная теорема Виноградова о 3 простых числах согласно гипотезе Римана» (PDF) . Электронные объявления об исследованиях Американского математического общества . 3 (15): 99–104. дои : 10.1090/S1079-6762-97-00031-0 .
Монтгомери, HL; Воан, RC (1975). «Исключительное множество в задаче Гольдбаха» (PDF) . Акта Арифметика . 27 : 353–370. дои : 10.4064/aa-27-1-353-370 .
Теренс Тао доказал, что все нечетные числа являются не более чем суммой пяти простых чисел .
Гипотеза Гольдбаха в MathWorld .

Внешние ссылки [ править ]

СМИ, связанные с гипотезой Гольдбаха, на Викискладе?
«Проблема Гольдбаха» , Математическая энциклопедия , EMS Press , 2001 [1994]
Оригинал письма Гольдбаха Эйлеру - формат PDF (на немецком и латыни)
Гипотеза Гольдбаха , часть книги Криса Колдуэлла «Prime Pages» .
Проверка гипотезы Гольдбаха , распределенный компьютерный поиск Томаса Оливейры и Сильвы.

[1] Математическое и физическое соответствие некоторых известных геометров XVIII века (Группа 1), СПб. 1843, стр. 125–129 .

[2] ttp://www.math.dartmouth.edu/~euler/correspondence/letters/OO0765.pdf ^{[ пустой URL PDF ]}

[MathWorldConj-3] Вайсштейн, Эрик В. «Гипотеза Гольдбаха» . Математический мир .

[4] В печатной версии, опубликованной PH Fuss [1] в маргинальной гипотезе 2 ошибочно напечатано как 1.

[5] ttp://eulerarchive.maa.org//correspondence/letters/OO0766.pdf. ^{[ пустой URL PDF ]}

[theorema-6] Ингэм, А.Е. «Популярные лекции» (PDF) . Архивировано из оригинала (PDF) 16 июня 2003 г. Проверено 23 сентября 2009 г.

[PrimeGlossary-7] Колдуэлл, Крис (2008). «Гипотеза Гольдбаха» . Проверено 13 августа 2008 г.

[8] Чудаков, Николаи Г. (1937). " О проблеме Гольдбаха" [ On the Goldbach problem ]. Doklady Akademii Nauk SSSR . 17 : 335-338.

[9] Ван дер Корпут, JG (1938). «О гипотезе Гольдбаха» (PDF) . Учеб. Акад. Влажный. Амстердам (на французском языке). 41 :76–80.

[10] Эстерманн, Т. (1938). «О проблеме Гольдбаха: доказательство того, что почти все четные положительные целые числа являются суммами двух простых чисел». Учеб. Лондонская математика. Соц . 2. 44 : 307–314. дои : 10.1112/plms/s2-44.4.307 .

[11] Шнирельманн, LG (1930). « Об аддитивных свойствах чисел », впервые опубликовано в «Записках Донского политехнического института в Новочеркасске» (на русском языке), т. 14 (1930), с. 3–27, и перепечатано в «Успехах математических наук» (на русском языке). ), 1939, вып. 6, 9–25.

[12] Шнирельманн, Л.Г. (1933). Впервые опубликовано под названием « Об аддитивных свойствах чисел » в « Mathematische Annalen » (на немецком языке), том. 107 (1933), 649–690 и перепечатано как « Об аддитивных свойствах чисел » в «Успехах математических наук», 1940, вып. 7, 7–46.

[13] Хелфготт, ХА (2013). «Тройная гипотеза Гольдбаха верна». arXiv : 1312.7748 [ math.NT ].

[14] Синисало, Матти К. (октябрь 1993 г.). «Проверка гипотезы Гольдбаха до 4 ⋅ 10 ¹¹ Математика (PDF) . вычислений . 61 (204). Американское математическое общество: 931–934. CiteSeerX 10.1.1.364.3111 . doi : 10.2307/2153264 . JSTOR 2153264 .

[15] Рассиас, М.Т. (2017). Проблема Гольдбаха: избранные темы . Спрингер.

[16] См., например, « Новую явную формулу аддитивной теории простых чисел с приложениями I. Явную формулу для задач Гольдбаха и обобщенных проблем простых чисел-близнецов» Яноша Пинца.

[Alfréd_Rényi_1948-17] Реньи, А.А. (1948). «О представлении четного числа в виде суммы простого и почти простого». Известия Академии Наук СССР Серия Математическая (на русском языке). 12 : 57–78.

[18] Чен, младший (1973). «О представлении большего четного целого числа в виде суммы простого числа и произведения не более двух простых чисел». наук. Синица . 16 : 157–176.

[19] Пинц, Дж .; Ружа, ИЗ (01.08.2020). «О приближении Линника к задаче Гольдбаха. II» . Acta Mathematica Hungarica . 161 (2): 569–582. дои : 10.1007/s10474-020-01077-8 . ISSN 1588-2632 . S2CID 54613256 .

[20] Хит-Браун, ДР; Пухта, Дж. К. (2002). «Целые числа представлены как сумма простых чисел и степеней двойки». Азиатский математический журнал . 6 (3): 535–565. arXiv : math.NT/0201299 . Бибкод : 2002math......1299H . дои : 10.4310/AJM.2002.v6.n3.a7 . S2CID 2843509 .

[Helfgott_2013-21] Хелфготт, ХА (2013). «Основные дуги теоремы Гольдбаха». arXiv : 1305.2897 [ math.NT ].

[Helfgott_2012-22] Хелфготт, ХА (2012). «Второстепенные дуги проблемы Гольдбаха». arXiv : 1205.5252 [ math.NT ].

[23] «Харальд Андрес Хелфготт» . Институт математики Жюсье-Париж Рив Гош . Проверено 06 апреля 2021 г.

[24] Пиппинг, Нильс (1890–1982), «Гипотеза Гольдбаха и теорема Гольдбаха-Виноградова». Акта Акад. Абоэнсис, Матем. 11, 4–25, 1938.

[25] Томас Оливейра и Силва, Проверка гипотезы Гольдбаха . Проверено 20 апреля 2024 г.

[26] Микаэла Калли-Хугилл и Адриан В. Дудек, Явная оценка среднего значения для PNT в интервалах

[27] «Математическая фантастика: ты никого не знаешь (Мишель Ричмонд)» . kasmana.people.cofc.edu .

[28] Одиль Морен Теорема Маргариты , в ФранцияИнформация:культура

[29] Флигель, Генри Ф.; Робертсон, Дуглас С. (1989). «Комета Гольдбаха: числа, связанные с гипотезой Гольдбаха». Журнал развлекательной математики . 21 (1): 1–7.

[30] Слоан, Нью-Джерси (ред.). «Последовательность A066352 (последовательность Пиллаи)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.

[31] Журнал Mathematics , 66:1 (1993): 45–47.

[32] Маргенштерн, М. (1984). «Результаты и предположения о практических числах». Известия Академии наук . 299 : 895–898.

[33] Мелфи, Г. (1996). «О двух предположениях о практических числах» . Журнал теории чисел . 56 : 205–210. дои : 10.1006/jnth.1996.0012 .

[34] «Гипотезы ПРАЙМ-БЛИЗНЕЦ» (PDF) . oeis.org .

[35] Слоан, Нью-Джерси (ред.). «Последовательность A007534 (Четные числа, не являющиеся суммой пары простых чисел-близнецов)» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]