Гипотеза Андрики

(а) Функция

A_{n}

для первых 100 простых чисел.

(б) Функция

A_{n}

для первых 200 простых чисел.

(в) Функция

A_{n}

для первых 500 простых чисел.

Графическое доказательство гипотезы Андрики для первых (a) 100, (b) 200 и (c) 500 простых чисел. Предполагается, что функция

A_{n}

всегда меньше 1.

Гипотеза Андрики (названная в честь румынского математика Дорина Андрики ) — это гипотеза относительно промежутков между простыми числами . ^{[ 1 ]}

Гипотеза утверждает, что неравенство

{\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}<1

держится для всех $n$ , где $p_{n}$ - е — n простое число. Если $g_{n}=p_{n+1}-p_{n}$ обозначает n- й простой пробел , то гипотезу Андрики также можно переписать как

g_{n}<2{\sqrt {p_{n}}}+1.

Эмпирические данные

Имран Гори использовал данные о крупнейших разрывах простых чисел, чтобы подтвердить гипотезу о $n$ до 1,3002 × 10 ¹⁶. ^{[ 2 ]} Используя таблицу максимальных пробелов и приведенное выше неравенство пробелов, значение подтверждения можно исчерпывающе расширить до 4 × 10. ¹⁸.

Дискретная функция $A_{n}={\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}$ изображено на рисунках напротив. Высшие отметки для $A_{n}$ встречаются при n = 1, 2 и 4, с A ₄ ≈ 0,670873..., без большего значения среди первых 10 ⁵ простые числа. Поскольку функция Андрики асимптотически убывает с увеличением n , необходим простой разрыв постоянно увеличивающегося размера, чтобы разница была большой по мере того, как n становится большим. Поэтому представляется весьма вероятным, что эта гипотеза верна, хотя это еще не доказано.

Обобщения

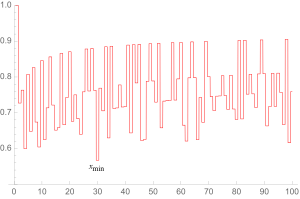
В качестве обобщения гипотезы Андрики рассматривалось следующее уравнение:

p_{n+1}^{x}-p_{n}^{x}=1,

где $p_{n}$ — n- е простое число, а x может быть любым положительным числом.

наибольшее возможное решение для x Легко видеть, что возникает при n = 1, когда x _max наименьшее решение для x = 1. Предполагается, что равно x _min ≈ 0,567148... (последовательность A038458 в OEIS ), которое возникает при n = 30.

Эта гипотеза также была сформулирована как неравенство , обобщенная гипотеза Андрики:

p_{n+1}^{x}-p_{n}^{x}<1

для

x<x_{\min }.

См. также

Ссылки и примечания

^ Андрика, Д. (1986). «Заметка о гипотезе из теории простых чисел». Студия Унив. Детки – Боляй Математика . 31 (4): 44–48. ISSN 0252-1938 . Збл 0623.10030 .
^ Уэллс, Дэвид (18 мая 2005 г.). Простые числа: самые загадочные цифры в математике . Хобокен (Нью-Джерси): Уайли. п. 13. ISBN 978-0-471-46234-7 .

Гай, Ричард К. (2004). «Раздел А8». Нерешенные проблемы теории чисел (3-е изд.). Спрингер-Верлаг . ISBN 978-0-387-20860-2 . Збл 1058.11001 .

Внешние ссылки

[1] Андрика, Д. (1986). «Заметка о гипотезе из теории простых чисел». Студия Унив. Детки – Боляй Математика . 31 (4): 44–48. ISSN 0252-1938 . Збл 0623.10030 .

[Wells_2005_prime_numbers-2] Уэллс, Дэвид (18 мая 2005 г.). Простые числа: самые загадочные цифры в математике . Хобокен (Нью-Джерси): Уайли. п. 13. ISBN 978-0-471-46234-7 .

[ 1 ]

[ 2 ]