Преобразование Фурье
| Преобразования Фурье |
|---|

В физике , технике и математике ( преобразование Фурье FT ) — это интегральное преобразование , которое принимает функцию в качестве входных данных и выводит другую функцию, описывающую степень присутствия различных частот в исходной функции. Результатом преобразования является комплексная функция частоты. Термин «преобразование Фурье» относится как к этой комплексной функции, так и к математической операции . Когда необходимо провести различие, преобразование Фурье иногда называют в частотной области представлением исходной функции . Преобразование Фурье аналогично разложению звука музыкального аккорда на интенсивности составляющих его звуков .

Функции, локализованные во временной области, имеют преобразования Фурье, которые распространяются по частотной области, и наоборот, это явление известно как принцип неопределенности . Критическим нормальное случаем для этого принципа является функция Гаусса , имеющая существенное значение в теории вероятностей и статистике , а также при изучении физических явлений, демонстрирующих распределение (например, диффузию ). Преобразование Фурье функции Гаусса — это еще одна функция Гаусса. Жозеф Фурье ввел это преобразование в своем исследовании теплопередачи , где функции Гаусса появляются как решения уравнения теплопроводности .
Преобразование Фурье можно формально определить как несобственный интеграл Римана , что делает его интегральным преобразованием, хотя это определение не подходит для многих приложений, требующих более сложной теории интегрирования. [примечание 1] Например, во многих относительно простых приложениях используется дельта-функция Дирака , которую формально можно рассматривать как функцию, но для обоснования требуется математически более сложная точка зрения. [примечание 2]
Преобразование Фурье также можно обобщить на функции нескольких переменных в евклидовом пространстве , превращая функцию трехмерного «позиционного пространства» в функцию трехмерного импульса (или функцию пространства и времени в функцию четырехмерного импульса). ). Эта идея делает пространственное преобразование Фурье очень естественным при изучении волн, а также в квантовой механике , где важно уметь представлять волновые решения как функции положения или импульса, а иногда и того и другого. В общем, функции, к которым применимы методы Фурье, являются комплекснозначными и, возможно, векторнозначными . [примечание 3] Еще дальнейшее обобщение возможно для функций на группах , которые, помимо исходного преобразования Фурье на R или R н , в частности включает преобразование Фурье с дискретным временем (DTFT, группа = Z ), дискретное преобразование Фурье (DFT, группа = Z mod N ) и ряд Фурье или круговое преобразование Фурье (группа = S 1 , единичная окружность ≈ замкнутый конечный интервал с отождествленными концами). Последний обычно используется для обработки периодических функций . Быстрое преобразование Фурье (БПФ) — это алгоритм вычисления ДПФ.
Определение [ править ]
Преобразование Фурье — это процесс анализа , разлагающий комплексную функцию. на составляющие его частоты и их амплитуды. Обратный процесс — синтез , воссоздающий от его преобразования.
Мы можем начать с аналогии — ряда Фурье , который анализирует на ограниченном интервале для некоторого положительного действительного числа Составляющие частоты представляют собой дискретный набор гармоник на частотах амплитуда и фаза которого определяются формулой анализа:
Аналогия с функцией можно получить формально из формулы анализа, приняв предел как , одновременно принимая так что [1] [2] [3] Формально выполняя это, получим для быстро убывающих : [примечание 4] [4]
| ( Уравнение 1 ) |
Легко видеть, если предположить гипотезу быстрого убывания, что интеграл (1) сходится при всех действительных , и (используя лемму Римана–Лебега ) что преобразованная функция также быстро снижается. Справедливость этого определения для классов функций которые не обязательно быстро уменьшаются, обсуждаются далее в этом разделе.
Оценка уравнения 1 для всех значений производит функцию частотной области . Комплексное число , в полярных координатах, передает как амплитуду , так и фазу частоты. Интуитивная интерпретация уравнения 1 заключается в том, что эффект умножения к это вычесть от каждой частотной составляющей функции [примечание 5] Только тот компонент, который был на частоте может дать ненулевое значение бесконечного интеграла, поскольку (по крайней мере формально) все остальные сдвинутые компоненты являются колебательными и интегрируются до нуля. (см. § Пример )
Соответствующая формула синтеза такой функции:
| ( Уравнение 2 ) |
Уравнение 2 представляет собой представление как взвешенное суммирование комплексных показательных функций.
Это также известно как теорема обращения Фурье и впервые было введено в Фурье «Аналитической теории тепла» . [5] [6] [7] [8]
Функции и называются парой преобразований Фурье . [9] Обычное обозначение для обозначения пар преобразований: [10]
Определение интегрируемых Лебегу по функций
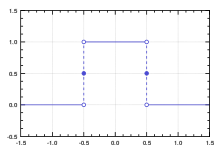
До сих пор мы имели дело с быстро убывающими на бесконечности функциями Шварца со всеми производными. Это исключает из определения многие функции, имеющие практическое значение, например функцию rect . функция Измеримая называется интегрируемым (по Лебегу), если интеграл Лебега по его абсолютному значению конечен:
Определение . Преобразование Фурье интегрируемой по Лебегу функции. определяется по формуле (1) .
Интегральное уравнение (1) четко определено для всех из-за предположения . (Можно показать, что функция ограничена и равномерно непрерывна в частотной области и, более того, по лемме Римана–Лебега равна нулю на бесконечности.)
Однако класс интегрируемых по Лебегу функций не идеален с точки зрения преобразования Фурье, поскольку не существует простой характеристики изображения и, следовательно, простой характеристики обратного преобразования.
функций, интегрируемых квадратом Унитарность и определение с
Хотя уравнение 1 определяет преобразование Фурье для (комплекснозначных) функций в , легко видеть, что он не вполне определен для других классов интегрируемости, особенно . Для функций в и с учетом соглашений уравнения 1 преобразование Фурье является унитарным оператором относительно скалярного произведения Гильберта на , ограниченный плотным подпространством интегрируемых функций. Следовательно, он допускает единственное непрерывное продолжение до унитарного оператора на , также называемое преобразованием Фурье. Это расширение важно отчасти потому, что преобразование Фурье сохраняет пространство так что, в отличие от случая , преобразование Фурье и обратное преобразование находятся в одном и том же основании, будучи преобразованиями одного и того же пространства функций в себя.
Важно отметить, что для функций в , преобразование Фурье больше не определяется уравнением 1 (интерпретируемым как интеграл Лебега). Например, функция находится в но не , поэтому интеграл (1) расходится. В таких случаях преобразование Фурье можно получить явно, регуляризируя интеграл и затем переходя к пределу. На практике интеграл часто рассматривается как несобственный интеграл вместо правильного интеграла Лебега, но иногда для сходимости необходимо использовать слабый предел или главное значение вместо (точечных) пределов, неявных в несобственном интеграле. Титчмарш (1986) и Дим и Маккин (1985) предлагают по три строгих способа расширения преобразования Фурье до интегрируемых с квадратом функций с использованием этой процедуры.
Соглашения, выбранные в этой статье, относятся к гармоническому анализу и характеризуются как уникальные соглашения, такие, что преобразование Фурье является унитарным на L 2 и гомоморфизм алгебры из L 1 в Л ∞ , без перенормировки меры Лебега. [12]
Угловая частота ( ω ) [ править ]
Когда независимая переменная ( ) представляет время (часто обозначается ), переменная преобразования ( ) представляет частоту (часто обозначается ). Например, если время измеряется в секундах , то частота — в герцах . Преобразование Фурье также можно записать через угловую частоту : единицы измерения — радианы в секунду.
Замена в уравнение 1 дает это соглашение, где функция перемаркирован
| обычная частота ξ (Гц) | унитарный | |
|---|---|---|
| угловая частота ω (рад/с) | унитарный | |
| неунитарный |
| обычная частота ξ (Гц) | унитарный | |
|---|---|---|
| угловая частота ω (рад/с) | унитарный | |
| неунитарный |
Расширение определения [ править ]
Для , преобразование Фурье можно определить на по интерполяции Марцинкевича .
Преобразование Фурье может быть определено в областях, отличных от действительной линии. Преобразование Фурье в евклидовом пространстве и преобразование Фурье в локально абелевых группах обсуждаются далее в статье.
Преобразование Фурье также можно определить для умеренных распределений , двойственных пространству быстро убывающих функций ( функций Шварца ). Функция Шварца — это гладкая функция, убывающая на бесконечности вместе со всеми своими производными. Пространство функций Шварца обозначается через , и его двойственный — пространство умеренных распределений. Дифференцируя под интегралом и применяя лемму Римана-Лебега, легко увидеть, что преобразование Фурье функции Шварца (определяемой формулой (1 )) снова является функцией Шварца. Преобразование Фурье умеренного распределения определяется двойственностью:
Существует множество других характеристик преобразования Фурье. Например, используется теорема Стоуна-фон Неймана : преобразование Фурье является уникальным унитарным переплетателем симплектического и евклидова представлений Шрёдингера группы Гейзенберга .
Предыстория [ править ]
История [ править ]
В 1822 году Фурье заявил (см. Жозеф Фурье § Аналитическая теория тепла ), что любую функцию, как непрерывную, так и прерывистую, можно разложить в ряд синусов. [13] Эта важная работа была исправлена и расширена другими, чтобы обеспечить основу для различных форм преобразования Фурье, используемых с тех пор.

Сложные синусоиды [ править ]
В целом коэффициенты — комплексные числа, имеющие две эквивалентные формы (см. формулу Эйлера ):
Продукт с ( Уравнение 2 ) имеет следующие формы:
Примечательно, насколько легко было упрощено произведение с использованием полярной формы и как легко была выведена прямоугольная форма с помощью формулы Эйлера.
Отрицательная частота [ править ]
Формула Эйлера вводит возможность отрицательного И уравнение 1 определено Только некоторые комплексные значения иметь преобразования (См. Аналитический сигнал . Простой пример: ) Но отрицательная частота необходима для характеристики всех остальных комплексных значений. встречается в обработке сигналов , уравнениях в частных производных , радиолокации , нелинейной оптике , квантовой механике и других.
Для реальной стоимости Уравнение 1 обладает свойством симметрии (см. § Сопряжение ниже). Эта избыточность позволяет уравнению 2 различать от Но, конечно, он не может сказать нам действительный признак потому что и неразличимы только на линии действительных чисел.
Фурье для периодических функций Преобразование
Преобразование Фурье периодической функции нельзя определить непосредственно с помощью интегральной формулы. Чтобы интеграл в уравнении 1, определить функция должна быть абсолютно интегрируемой . Вместо этого обычно используют ряд Фурье . Можно расширить определение, включив в него периодические функции, рассматривая их как умеренные распределения .
Это позволяет увидеть связь между рядом Фурье и преобразованием Фурье для периодических функций, имеющих сходящийся ряд Фурье . Если — периодическая функция с периодом , имеющий сходящийся ряд Фурье, то:
Фурье преобразования Выборка
Преобразование Фурье интегрируемой функции можно отбирать через регулярные промежутки времени произвольной длины Эти выборки можно вывести из одного цикла периодической функции. который имеет коэффициенты ряда Фурье , пропорциональные этим выборкам по формуле суммирования Пуассона :
Интегрируемость обеспечивает сходимость периодического суммирования. Таким образом, образцы можно определить с помощью анализа рядов Фурье:
Когда имеет компактную поддержку , имеет конечное число членов на интервале интегрирования. Когда не имеет компактного носителя, числовая оценка требует приближения, такого как сужение или усечение количества терминов.
Пример [ править ]
Следующие рисунки наглядно иллюстрируют, как преобразование Фурье измеряет наличие частоты в конкретной функции. Изображенная функция колеблется с частотой 3 Гц (если измеряет секунды) и быстро стремится к 0. (Второй фактор в этом уравнении — это огибающая , которая преобразует непрерывную синусоиду в короткий импульс.). был специально выбран для того, чтобы иметь реальное преобразование Фурье, которое можно легко построить. Первое изображение — это его график. Чтобы вычислить мы должны интегрировать продукт Следующие два изображения — это реальные и воображаемые части этого продукта. Действительная часть подынтегральной функции имеет неотрицательное среднее значение, поскольку чередующиеся знаки и колеблются с той же скоростью и той же фазой, тогда как и имеют одинаковую скорость, но ортогональную фазу. В результате при интегрировании действительной части подынтегральной функции вы получите относительно большое число (в данном случае ). Кроме того, когда вы пытаетесь измерить частоту, которой нет, как в случае, когда мы смотрим на как действительная, так и мнимая составляющая продукта быстро колеблются между положительными и отрицательными значениями. Следовательно, интеграл очень мал, а значение преобразования Фурье для этой частоты близко к нулю. Общая ситуация обычно более сложна, но эвристически именно так преобразование Фурье измеряет, какая часть отдельной частоты присутствует в функции.
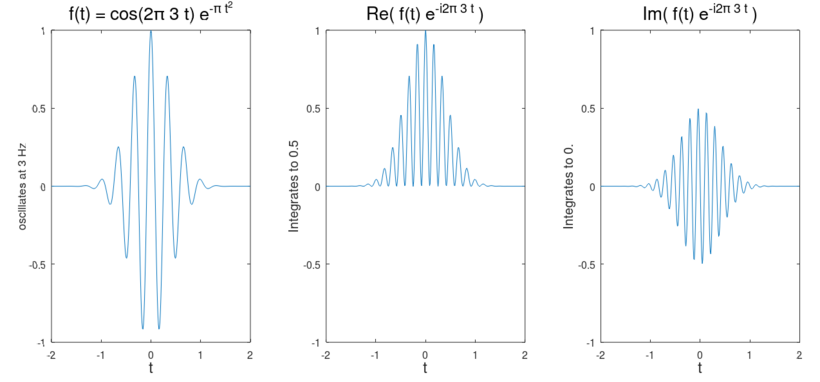
- Действительная и мнимая части подынтегрального выражения для преобразования Фурье при частоте 5 Гц
- Величина преобразования Фурье с пометкой 3 и 5 Гц.
Чтобы подтвердить предыдущий пункт, причина ответа на Гц, потому что и неразличимы. Преобразование будет иметь только один ответ, амплитуда которого является интегралом гладкой огибающей: тогда как (второй график выше)
преобразования Фурье Свойства
Позволять и представляют собой интегрируемые функции , измеримые по Лебегу на прямой, удовлетворяющие:
Основные свойства [ править ]
Преобразование Фурье обладает следующими основными свойствами: [14]
Линейность [ править ]
Сдвиг времени [ править ]
Сдвиг частоты [ править ]
Масштабирование времени [ править ]
Симметрия [ править ]
Когда действительная и мнимая части сложной функции разлагаются на четные и нечетные части , получается четыре компонента, обозначенные ниже индексами RE, RO, IE и IO. Между четырьмя компонентами комплексной функции времени и четырьмя компонентами ее комплексного частотного преобразования существует взаимно однозначное соответствие:
Отсюда вытекают различные зависимости, например :
- Преобразование действительной функции это четная симметричная функция И наоборот, четно-симметричное преобразование подразумевает вещественную временную область.
- Преобразование мнимой функции нечетная симметричная функция и обратное верно.
- Преобразование четно-симметричной функции это действительная функция и обратное верно.
- Преобразование нечетно-симметричной функции — мнимая функция и обратное верно.
Спряжение [ править ]
В частности, если реально тогда , даже симметрична (она же эрмитова функция ):
И если является чисто воображаемым, то нечетно симметричен :
Реальная и мнимая части времени [ править ]
Компонент нулевой частоты [ править ]
Замена в определении получаем:
Интеграл в своей области известен как среднее значение или смещение постоянного тока функции.
Обратимость и периодичность [ править ]
При подходящих условиях на функции , его можно восстановить с помощью преобразования Фурье . Действительно, обозначая оператор преобразования Фурье через , так , то для подходящих функций двукратное применение преобразования Фурье просто переворачивает функцию: , что можно интерпретировать как «обратное время». Поскольку время реверса является двухпериодическим, применение этого дважды дает , поэтому оператор преобразования Фурье является четырехпериодическим, и аналогично обратное преобразование Фурье можно получить, применив преобразование Фурье три раза: . В частности, преобразование Фурье обратимо (при подходящих условиях).
Точнее, определение оператора четности такой, что , у нас есть:
Эта четырехкратная периодичность преобразования Фурье аналогична повороту плоскости на 90°, особенно потому, что двукратная итерация приводит к развороту, и на самом деле эту аналогию можно уточнить. Хотя преобразование Фурье можно просто интерпретировать как переключение временной области и частотной области, а обратное преобразование Фурье переключает их обратно, более геометрически его можно интерпретировать как поворот на 90 ° во временной и частотной области (рассматривая время как ось x и частота как ось y ), а преобразование Фурье можно обобщить до дробного преобразования Фурье , которое включает повороты на другие углы. Это можно далее обобщить на линейные канонические преобразования , которые можно визуализировать как действие специальной линейной группы SL 2 ( R ) на плоскости время-частота с сохраненной симплектической формой, соответствующей принципу неопределенности , ниже. Этот подход особенно изучается при обработке сигналов , при частотно-временном анализе .
Единицы [ править ]
Частотная переменная должна иметь единицы измерения, обратные единицам области определения исходной функции (обычно называемые t или x ). Например, если t измеряется в секундах, ξ должно быть в циклах в секунду или герцах . Если шкала времени измеряется в единицах 2 π секунд, то другая греческая буква ω вместо этого обычно используется для обозначения угловой частоты (где ω = 2π ξ ) в единицах радиан в секунду. Если использовать x для единиц длины, то ξ должна иметь обратную длину, например, волновые числа . Другими словами, существует две версии реальной линии: одна представляет собой диапазон t и , а измеряется в единицах t другая представляет собой диапазон ξ и измеряется в единицах, обратных единицам t . Эти две разные версии реальной линии нельзя приравнивать друг к другу. Следовательно, преобразование Фурье переходит из одного пространства функций в другое пространство функций: функции, имеющие другую область определения.
В общем, ξ всегда следует рассматривать как линейную форму в пространстве своей области определения, то есть вторая вещественная линия является пространством, двойственным к первой вещественной прямой. См. статью о линейной алгебре для более формального объяснения и более подробной информации. Эта точка зрения становится существенной при обобщениях преобразования Фурье на группы общей симметрии , включая случай рядов Фурье.
Не существует единого предпочтительного способа (часто говорят «нет канонического способа») сравнения двух версий реальной линии, которые участвуют в преобразовании Фурье — фиксация единиц измерения на одной линии не приводит к изменению масштаба единиц измерения на другая линия — причина множества конкурирующих соглашений по определению преобразования Фурье. Различные определения, возникающие в результате различного выбора единиц измерения, различаются разными константами.
В других соглашениях преобразование Фурье имеет i в показателе степени вместо − i , и наоборот для формулы обращения. Это соглашение распространено в современной физике. [15] и является значением по умолчанию для Wolfram Alpha и не означает, что частота стала отрицательной, поскольку не существует канонического определения положительности частоты сложной волны. Это просто означает, что это амплитуда волны вместо волны (первый, со знаком минус, часто наблюдается во временной зависимости для синусоидальных плоских волновых решений уравнения электромагнитных волн или во временной зависимости для квантовых волновых функций ). Многие тождества, включающие преобразование Фурье, остаются в силе в этих соглашениях при условии, что все термины, которые явно включают i, заменяются на - i . В электротехнике буква j обычно используется для мнимой единицы вместо i, потому что i используется для обозначения тока.
При использовании безразмерных единиц постоянные коэффициенты могут даже не быть записаны в определении преобразования. Например, в теории вероятностей характеристическая функция Φ функции плотности вероятности f случайной величины X непрерывного типа определяется без отрицательного знака в экспоненте, а поскольку единицы x игнорируются, то нет 2 π. и :
(В теории вероятностей и в математической статистике использование преобразования Фурье — Стилтьеса является предпочтительным, поскольку многие случайные величины не имеют непрерывного типа и не обладают функцией плотности, и приходится рассматривать не функции, а распределения , т. е. , меры, обладающие «атомами».)
С более высокой точки зрения групповых характеров , которая гораздо более абстрактна, все эти произвольные выборы исчезают, как будет объяснено в следующем разделе этой статьи, где рассматривается понятие преобразования Фурье функции на локально компактном абелевом элементе. группа .
Римана – Равномерная Лебега непрерывность и лемма
Преобразование Фурье может быть определено в некоторых случаях для неинтегрируемых функций, но преобразования Фурье интегрируемых функций обладают несколькими сильными свойствами.
Преобразование Фурье f̂ любой интегрируемой функции f непрерывно равномерно и [16]
По лемме Римана– Лебега [11]
Однако, не обязательно должно быть интегрируемым. Например, преобразование Фурье прямоугольной функции , которая является интегрируемой, представляет собой функцию sinc , которая не является интегрируемой по Лебегу , поскольку ее несобственные интегралы ведут себя аналогично знакопеременному гармоническому ряду , сходясь к сумме, не будучи абсолютно сходящимся .
невозможно записать Обычно обратное преобразование в виде интеграла Лебега . Однако, когда и f , и интегрируемы, то обратное равенство
Парсеваля теорема и Теорема Планшереля
Пусть f ( x ) и g ( x ) интегрируемы, и пусть f̂ ( ξ ) и ĝ ( ξ ) — их преобразования Фурье. Если f ( x ) и g ( x ) также интегрируемы с квадратом , то формула Парсеваля следующая: [17]
Теорема Планшереля , следующая из вышеизложенного, утверждает, что [18]
Теорема Планшереля позволяет расширить преобразование Фурье с помощью аргумента непрерывности до унитарного оператора на L 2 ( Р ) . На Л 1 ( р ) ∩ L 2 ( R ) это расширение согласуется с исходным преобразованием Фурье, определенным на L 1 ( R ) , тем самым расширяя область преобразования Фурье до L 1 ( р ) + л 2 ( R ) (и, следовательно, к L п ( р ) для 1 ≤ п ≤ 2 ). Теорема Планшереля имеет в науках интерпретацию, согласно которой преобразование Фурье сохраняет энергию исходной величины. Терминология этих формул не совсем стандартизирована. Теорема Парсеваля была доказана только для рядов Фурье и впервые доказана Ляпуновым. Но формула Парсеваля имеет смысл и для преобразования Фурье, и поэтому, хотя в контексте преобразования Фурье она была доказана Планшерелем, ее до сих пор часто называют формулой Парсеваля, соотношением Парсеваля или даже теоремой Парсеваля.
См. Двойственность Понтрягина для получения общей формулировки этой концепции в контексте локально компактных абелевых групп.
Формула суммирования Пуассона
Формула суммирования Пуассона (PSF) представляет собой уравнение, которое связывает ряда Фурье коэффициенты периодического суммирования функции со значениями непрерывного преобразования Фурье функции. Формула суммирования Пуассона гласит, что для достаточно регулярных функций f ,
Он имеет множество полезных форм, которые получены из базовой формы путем применения свойств масштабирования и сдвига во времени преобразования Фурье. Формула находит применение в технике, физике и теории чисел . Двойственная стандартная формула суммирования Пуассона в частотной области также называется преобразованием Фурье дискретного времени .
Суммирование Пуассона обычно связано с физикой периодических сред, например, с теплопроводностью по кругу. Фундаментальное решение уравнения теплопроводности на окружности называется тэта-функцией . Он используется в теории чисел для доказательства свойств преобразования тэта-функций, которые оказываются разновидностью модулярной формы , и в более общем плане связан с теорией автоморфных форм , где он появляется на одной стороне формулы следа Сельберга .
Дифференциация [ править ]
Предположим, f ( x ) — абсолютно непрерывная дифференцируемая функция, и как f , так и ее производная f′ интегрируемы. Тогда преобразование Фурье производной имеет вид
Аналогично, , так
Применяя преобразование Фурье и используя эти формулы, некоторые обыкновенные дифференциальные уравнения можно преобразовать в алгебраические уравнения, которые гораздо легче решать. Эти формулы также приводят к практическому правилу: « f ( x ) является гладким тогда и только тогда, когда f̂ ( ξ ) быстро падает до 0 при | ξ | → ∞ ». Используя аналогичные правила для обратного преобразования Фурье, можно также сказать: « f ( x ) быстро падает до 0 при | x | → ∞ тогда и только тогда, когда f̂ ( ξ ) является гладким».
Теорема о свертке
Преобразование Фурье выполняет преобразование между сверткой и умножением функций. Если f ( x ) и g ( x ) являются интегрируемыми функциями с преобразованиями Фурье f̂ ( ξ ) и ĝ ( ξ ) соответственно, то преобразование Фурье свертки задается произведением преобразований Фурье f̂ ( ξ ) и ĝ ( ξ ) (при других соглашениях для определения преобразования Фурье может фигурировать постоянный множитель).
Это означает, что если:
В теории систем с линейным инвариантом во времени (LTI) принято интерпретировать g ( x ) как импульсную характеристику системы LTI с входом f ( x ) и выходом h ( x ) , поскольку замена импульсом единичным f ( x ) дает час ( Икс ) знак равно г ( Икс ) . В этом случае ĝ ( ξ ) представляет частотную характеристику системы.
И наоборот, если f ( x ) можно разложить как произведение двух суммируемых с квадратом функций p ( x ) и q ( x ) , то преобразование Фурье f ( x ) задается сверткой соответствующих преобразований Фурье p̂ ( ξ ) и q̂ ( ξ ) .
взаимной корреляции о Теорема
Аналогичным образом можно показать, что если ( x ) является взаимной корреляцией f ( ( x ) и g h x ) :
В частном случае автокорреляция функции f ( x ) равна:
Собственные функции [ править ]
Преобразование Фурье — это линейное преобразование, собственные функции которого подчиняются с
Набор собственных функций находится, если отметить, что однородное дифференциальное уравнение
В более общем смысле, набор собственных функций также находится, если отметить, что правила дифференцирования подразумевают, что обыкновенное дифференциальное уравнение
Согласно этому соглашению о преобразовании Фурье, мы имеем следующее:
Другими словами, функции Эрмита образуют полную ортонормированную систему собственных функций преобразования Фурье на L 2 ( Р ) . [14] [21] Однако такой выбор собственных функций не является единственным. Из-за существует только четыре различных собственных значения преобразования Фурье (корни четвертой степени из единицы ±1 и ± i ), и любая линейная комбинация собственных функций с одним и тем же собственным значением дает другую собственную функцию. [22] Вследствие этого можно разложить L 2 ( R ) как прямая сумма четырех пространств H 0 , H 1 , H 2 и H 3 , где преобразование Фурье действует на He k просто умножением на i к .
Поскольку полный набор функций Эрмита ψ n обеспечивает разрешение тождества, они диагонализуют оператор Фурье, т.е. преобразование Фурье может быть представлено такой суммой членов, взвешенных по указанным выше собственным значениям, и эти суммы можно суммировать явно:
Этот подход к определению преобразования Фурье был впервые предложен Норбертом Винером . [23] Помимо других свойств, функции Эрмита экспоненциально быстро убывают как в частотной, так и во временной области, и поэтому они используются для определения обобщения преобразования Фурье, а именно дробного преобразования Фурье, используемого в частотно-временном анализе. [24] В физике это преобразование было введено Эдвардом Кондоном . [25] Такое изменение базисных функций становится возможным, поскольку преобразование Фурье является унитарным преобразованием при использовании правильных соглашений . Следовательно, при соответствующих условиях можно ожидать, что это будет результатом самосопряженного генератора с помощью [26]
Оператор — числовой оператор квантового гармонического осциллятора, записанный в виде [27] [28]
Его можно интерпретировать как генератор дробных преобразований Фурье для произвольных значений t и обычного непрерывного преобразования Фурье. за конкретную стоимость с ядром Мелера, реализующим соответствующее активное преобразование . Собственные функции являются функциями Эрмита которые, следовательно, также являются собственными функциями
При распространении преобразования Фурье на распределения гребенка Дирака также является собственной функцией преобразования Фурье.
Связь с группой Гейзенберга [ править ]
Группа Гейзенберга — это некоторая группа унитарных операторов в гильбертовом пространстве L 2 ( R ) квадратично интегрируемых комплекснозначных функций f на вещественной прямой, порожденных сдвигами ( T y f )( x ) = f ( x + y ) и умножением на e я 2π ξx , ( M ξ ж )( Икс ) знак равно е я 2π ξx ж ( Икс ) . Эти операторы не коммутируют, так как их (групповой) коммутатор
Обозначим группу Гейзенберга через H 1 . процедура описывает не только структуру группы, но и стандартное унитарное представление H Вышеописанная 1 в гильбертовом пространстве, которое мы обозначим через ρ : H 1 → B ( L 2 ( Р )) . Определим линейный автоморфизм R 2 к
Согласно теореме Стоуна–фон Неймана унитарные представления ρ и ρ ∘ j унитарно эквивалентны, поэтому существует единственный переплетатель W ∈ U ( L 2 ( R )) такой, что
Многие из стандартных свойств преобразования Фурье являются непосредственными следствиями этой более общей схемы. [29] Например, квадрат преобразования Фурье W 2 , является переплетителем, связанным с J 2 = − I , и поэтому мы имеем ( W 2 f )( x ) = f (− x ) является отражением исходной функции f .
Сложный домен [ править ]
Интеграл для преобразования Фурье
Теорема Пэли–Винера гласит, что f является гладкой (т. е. n -раз дифференцируемой для всех положительных целых чисел n ) и имеет компактный носитель тогда и только тогда, когда f̂ ( σ + iτ ) — голоморфная функция , для которой существует константа a > 0, такая что для любого целого числа n ≥ 0 ,
(Если f не гладкое, а только L 2 , утверждение остается верным при условии n = 0 . [32] ) Пространство таких функций комплексной переменной называется пространством Пэли — Винера. Эта теорема была обобщена на полупростые группы Ли . [33]
Если f поддерживается на полупрямой t ≥ 0 , то f называется «причинным», потому что функция импульсной характеристики физически реализуемого фильтра должна обладать этим свойством, поскольку никакое следствие не может предшествовать его причине. Пэли и Винер показали, что тогда f̂ продолжается до голоморфной функции в комплексной нижней полуплоскости τ < 0 , которая стремится к нулю при стремлении τ к бесконечности. [34] Обратное неверно, и неизвестно, как охарактеризовать преобразование Фурье причинной функции. [35]
Преобразование Лапласа [ править ]
Преобразование Фурье f̂ ( ξ ) связано с преобразованием Лапласа F ( s ) , которое также используется для решения дифференциальных уравнений и анализа фильтров .
Может случиться так, что функция f, для которой интеграл Фурье вообще не сходится на вещественной оси, тем не менее имеет комплексное преобразование Фурье, определенное в некоторой области комплексной плоскости .
Например, если f ( t ) имеет экспоненциальный рост, т. е.
Более обычная версия («односторонняя») преобразования Лапласа:
Если f также является причинным и аналитическим, то: Таким образом, распространение преобразования Фурье на комплексную область означает, что оно включает преобразование Лапласа как частный случай в случае причинных функций, но с заменой переменной s = i 2π ξ .
С другой, возможно, более классической точки зрения, преобразование Лапласа по своей форме включает в себя дополнительный экспоненциальный регулирующий член, который позволяет ему сходиться за пределами воображаемой линии, где определено преобразование Фурье. По существу, оно может сходиться не более чем для экспоненциально расходящихся рядов и интегралов, тогда как исходное разложение Фурье не может, что позволяет анализировать системы с расходящимися или критическими элементами. Двумя конкретными примерами линейной обработки сигналов являются построение сетей всепропускающих фильтров из критических гребенчатых и смягчающих фильтров посредством точного подавления полюса-ноля на единичной окружности. Такие конструкции распространены при обработке звука, где требуется сильно нелинейная фазовая характеристика, например, в реверберации.
Более того, когда для обработки сигналов требуются расширенные импульсные характеристики, самый простой способ их создания — это иметь одну схему, которая создает расходящийся временной отклик, а затем компенсировать его расхождение посредством задержанного противоположного и компенсаторного отклика. Здесь только промежуточная схема задержки допускает классическое описание Фурье, что имеет решающее значение. Обе боковые схемы неустойчивы и не допускают сходящегося разложения Фурье. Однако они допускают описание области Лапласа с идентичными полуплоскостями сходимости в комплексной плоскости (или, в дискретном случае, в Z-плоскости), при этом их эффекты компенсируются.
В современной математике преобразование Лапласа традиционно относят к методам Фурье. Оба они подчинены гораздо более общей и более абстрактной идее гармонического анализа .
Инверсия [ править ]
Все еще с , если является комплексно-аналитическим при a ⩽ τ ⩽ b , то
Теорема: Если f ( t ) = 0 для t < 0 и | ж ( т ) | < Се а | т | для некоторых констант C , a > 0 , то
Из этой теоремы следует формула обращения Меллина для преобразования Лапласа: [36]
Гипотезы можно ослабить, как в результатах Карлесона и Ханта, до f ( t ) e − в быть Л 1 , при условии, что f имеет ограниченную вариацию в замкнутой окрестности точки t (см. теорему Дирихле–Дини ), значение f в точке t принимается как среднее арифметическое левого и правого пределов, и при условии, что интегралы берутся в смысле главных ценностей Коши. [38]
л 2 также доступны версии этих формул обращения. [39]
в евклидовом пространстве Преобразование Фурье
Преобразование Фурье может быть определено в любом произвольном количестве измерений n . Как и в одномерном случае, здесь существует множество соглашений. Для интегрируемой функции f ( x ) в этой статье используется определение:
Все перечисленные выше основные свойства справедливы для n -мерного преобразования Фурье, как и теорема Планшереля и Парсеваля. Когда функция интегрируема, преобразование Фурье по-прежнему равномерно непрерывно и лемма Римана – Лебега выполняется. [11]
Принцип неопределенности [ править ]
Вообще говоря, чем более концентрировано f ( x ) , тем более разбросанным его преобразование Фурье f̂ ( ξ ) должно быть . В частности, свойство масштабирования преобразования Фурье можно рассматривать следующим образом: если мы сжимаем функцию в x , ее преобразование Фурье растягивается в ξ . Невозможно произвольно сосредоточить одновременно функцию и ее преобразование Фурье.
Компромисс между сжатием функции и ее преобразованием Фурье можно формализовать в форме принципа неопределенности , рассматривая функцию и ее преобразование Фурье как сопряженные переменные относительно симплектической формы в частотно-временной области : из С точки зрения линейного канонического преобразования преобразование Фурье представляет собой поворот на 90° в частотно-временной области и сохраняет симплектическую форму .
Предположим, f ( x ) — интегрируемая и интегрируемая с квадратом функция. Без ограничения общности предположим, что f ( x ) нормализовано:
следует Из теоремы Планшереля , что f̂ ( ξ ) также нормирована.
Разброс вокруг x = 0 можно измерить по дисперсии около нуля. [40] определяется
это второй момент | С точки зрения вероятности , ж ( Икс ) | 2 около нуля.
Принцип неопределенности гласит, что если f ( x ) абсолютно непрерывна и функции x · f ( x ) и f ′ ( x ) интегрируемы с квадратом, то [14]
Равенство достигается только в случае
Фактически, это неравенство означает, что:
В квантовой механике волновые импульса и положения функции представляют собой пары преобразований Фурье с точностью до коэффициента постоянной Планка . При правильном учете этой константы приведенное выше неравенство становится формулировкой принципа неопределенности Гейзенберга . [42]
Более сильным принципом неопределенности является принцип неопределенности Хиршмана , который выражается как:
Синусные и косинусные преобразования [ править ]
В исходной формулировке преобразования Фурье использовались не комплексные числа, а скорее синусы и косинусы. Статистики и другие специалисты до сих пор используют эту форму. Абсолютно интегрируемая функция f, для которой выполняется обращение Фурье, может быть расширена в терминах истинных частот (избегая отрицательных частот, которые иногда считаются трудно интерпретируемыми физически). [43] ) λ по
Это называется разложением в тригонометрический интеграл или разложением в интеграл Фурье. Коэффициентные функции a и b можно найти с помощью вариантов косинусного преобразования Фурье и синусоидального преобразования Фурье (нормализации опять же не стандартизированы):
В более старой литературе упоминаются две функции преобразования: косинусное преобразование Фурье a и синусное преобразование Фурье b .
Функцию f можно восстановить из синусоидального и косинусного преобразования, используя
Сферические гармоники [ править ]
Пусть множество однородных гармонических полиномов степени k на R н обозначим через A k . Множество Ak k состоит из гармоник степени твердых сферических . Твердые сферические гармоники играют ту же роль в более высоких измерениях, что и полиномы Эрмита в первом измерении. В частности, если f ( x ) = e −π| х | 2 P ( x ) для некоторого P ( x ) в A k , то f̂ ( ξ ) = i - к ж ( ξ ) . Пусть множество H k является замыканием в L 2 ( Р н ) линейных комбинаций функций вида f (| x |) P ( x ) , где P ( x ) находится в A k . Пространство Л 2 ( Р н ) тогда является прямой суммой пространств Hk , Фурье отображает каждое пространство в Hk себя и позволяет охарактеризовать действие преобразования Фурье на каждое пространство Hk . и преобразование [11]
Пусть f ( x ) = f 0 (| x |) P ( x ) (с P ( x ) в A k ), тогда
Здесь J ( n + 2 k − 2)/2 обозначает функцию Бесселя первого рода с порядком п + 2 k - 2 / 2 . Когда k = 0, это дает полезную формулу преобразования Фурье радиальной функции. [47] По сути, это преобразование Ханкеля . Более того, существует простая рекурсия, связывающая случаи n + 2 и n [48] позволяющий вычислить, например, трехмерное преобразование Фурье радиальной функции по одномерной.
Проблемы с ограничениями [ править ]
В более высоких измерениях становится интересным изучить проблемы ограничения преобразования Фурье. Преобразование Фурье интегрируемой функции непрерывно и определено ограничение этой функции на любое множество. Но для функции, интегрируемой с квадратом, преобразование Фурье может быть общим классом функций, интегрируемых с квадратом. Таким образом, ограничение преобразования Фурье L 2 ( Р н ) функция не может быть определена на множествах меры 0. Это все еще активная область изучения, чтобы понять проблемы ограничения в L п для 1 < р < 2 . В некоторых случаях можно определить ограничение преобразования Фурье на набор S при условии, что S имеет ненулевую кривизну. Случай, когда S — единичная сфера в R н представляет особый интерес. В этом случае ограничительная теорема Томаса– Стейна утверждает, что ограничение преобразования Фурье на единичную сферу в R н является ограниченным оператором в L п при условии 1 ≤ p ≤ 2 н + 2 / н + 3 .
Одно заметное различие между преобразованием Фурье в одномерном измерении и в более высоких измерениях касается оператора частичной суммы. Рассмотрим возрастающий набор измеримых множеств E R с индексом R ∈ (0,∞) : таких как шары радиуса R с центром в начале координат или кубы со стороной 2 R . Для данной интегрируемой функции f рассмотрим функцию f R, определяемую формулой:
Предположим дополнительно, что f ∈ L п ( Р н ) . Для n = 1 и 1 < p < ∞ , если взять E R = (− R , R ) , то f R сходится к f в L п поскольку R стремится к бесконечности, в силу ограниченности преобразования Гильберта . Наивно можно надеяться, что то же самое справедливо и для n > 1 . Если в качестве E R взять куб с длиной стороны R , то сходимость сохраняется. Другим естественным кандидатом является евклидов шар E R = { ξ : | ξ | < Р } . Чтобы этот оператор частичной суммы сходился, необходимо, чтобы множитель единичного шара был ограничен в L п ( Р н ) . Для n ≥ 2 гласит знаменитая теорема Чарльза Феффермана , что множитель единичного шара никогда не ограничен, если только p = 2 . [23] Фактически, когда p ≠ 2 , это показывает, что не только f R может не сходиться к f в L п , но для некоторых функций f ∈ L п ( Р н ) , f R даже не является элементом L п .
Преобразование Фурье в функциональных пространствах [ править ]
Где Л п пробелы [ править ]
Где Л 1 [ редактировать ]
Определение преобразования Фурье по интегральной формуле
Преобразование Фурье F : L 1 ( Р н ) → Л ∞ ( Р н ) — ограниченный оператор . Это следует из наблюдения, что
Где Л 2 [ редактировать ]
Поскольку гладкие функции с компактным носителем интегрируемы и плотны в L 2 ( Р н ) теорема Планшереля позволяет распространить определение преобразования Фурье на общие функции из L 2 ( Р н ) по аргументам непрерывности. Преобразование Фурье в L 2 ( Р н ) больше не задается обычным интегралом Лебега, хотя его можно вычислить с помощью несобственного интеграла , здесь это означает, что для L 2 функция f ,
Многие свойства преобразования Фурье в L 1 перенести на Л 2 , с помощью подходящего ограничивающего аргумента.
Кроме того, F : L 2 ( Р н ) → Л 2 ( Р н ) — унитарный оператор . [50] Чтобы оператор был унитарным, достаточно показать, что он биективен и сохраняет скалярное произведение, поэтому в этом случае это следует из теоремы обращения Фурье в сочетании с тем фактом, что для любого f , g ∈ L 2 ( Р н ) у нас есть
В частности, образ Л. 2 ( Р н ) сам находится под преобразованием Фурье.
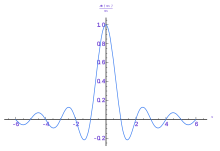
На другом Л п [ редактировать ]
Определение преобразования Фурье можно распространить на функции из L п ( Р н ) для 1 ≤ p ≤ 2 путем разложения таких функций на «толстый хвост» в L 2 плюс толстая часть тела в L 1 . В каждом из этих пространств преобразование Фурье функции из L п ( Р н ) находится в L д ( Р н ) , где q = p / p − 1 — сопряженное по Гельдеру число p (по неравенству Хаусдорфа–Юнга ). Однако, за исключением p = 2 , изображение нелегко охарактеризовать. Дальнейшие расширения становятся более техническими. Преобразование Фурье функций из L п для диапазона 2 < p < ∞ требует изучения распределений. [16] Фактически можно показать, что существуют функции из L п с p > 2, так что преобразование Фурье не определяется как функция. [11]
Умеренные дистрибутивы [ править ]
Можно рассмотреть возможность расширения области преобразования Фурье с L 1 + Л 2 рассматривая обобщенные функции или распределения. Распределение на R н — непрерывный линейный функционал в пространстве C c ( R н ) компактно поддерживаемых гладких функций, оснащенных подходящей топологией. Тогда стратегия состоит в том, чтобы рассмотреть действие преобразования Фурье на C c ( R н ) и перейдем к распределениям по двойственности. Препятствием для этого является то, что преобразование Фурье не отображает C c ( R н ) до C c ( R н ) . Фактически преобразование Фурье элемента из C c ( R н ) не может исчезнуть на открытом множестве; см. приведенное выше обсуждение принципа неопределенности. Правое пространство здесь — немного большее пространство функций Шварца . Преобразование Фурье является автоморфизмом в пространстве Шварца как топологическом векторном пространстве и, таким образом, индуцирует автоморфизм в его двойственном пространстве, пространстве умеренных распределений. [11] Умеренные распределения включают в себя все упомянутые выше интегрируемые функции, а также «хорошие» функции полиномиального роста и распределения с компактным носителем.
Для определения преобразования Фурье умеренного распределения пусть f и g — интегрируемые функции, а f̂ и ĝ — их преобразования Фурье соответственно. Тогда преобразование Фурье подчиняется следующей формуле умножения: [11]
Каждая интегрируемая функция f определяет (индуцирует) распределение T f соотношением
Распределения можно дифференцировать, и вышеупомянутая совместимость преобразования Фурье с дифференцированием и сверткой остается верной для умеренных распределений.
Обобщения [ править ]
- Преобразование Стилтьеса Фурье
Преобразование Фурье конечной борелевской меры µ на R н дается: [51]
Это преобразование продолжает обладать многими свойствами преобразования Фурье интегрируемых функций. Одно заметное отличие состоит в том, что лемма Римана–Лебега не работает для мер. [16] В случае, когда dμ = f ( x ) dx , приведенная выше формула сводится к обычному определению преобразования Фурье f . В случае, когда µ является распределением вероятностей, связанным со случайной величиной X , преобразование Фурье – Стилтьеса тесно связано с характеристической функцией , но типичные соглашения в теории вероятностей принимают e iξx вместо е − я 2π ξx . [14] В случае, когда распределение имеет функцию плотности вероятности, это определение сводится к преобразованию Фурье, примененному к функции плотности вероятности, опять же с другим выбором констант.
Преобразование Фурье можно использовать для характеристики мер. Теорема Бохнера характеризует, какие функции могут возникнуть как преобразование Фурье – Стилтьеса положительной меры на окружности. [16]
Более того, дельта-функция Дирака хоть и не является функцией, но является конечной борелевской мерой. Его преобразование Фурье является постоянной функцией (конкретное значение которой зависит от формы используемого преобразования Фурье).
абелевы Локально компактные группы
Преобразование Фурье можно обобщить на любую локально компактную абелеву группу. Локально компактная абелева группа — это абелева группа , которая в то же время является локально компактным топологическим пространством Хаусдорфа, так что групповая операция непрерывна. Если G — локально компактная абелева группа, она имеет трансляционно-инвариантную меру µ , называемую мерой Хаара . Для локально компактной абелевой группы G множество неприводимых, т. е. одномерных, унитарных представлений называются ее характерами . Со своей естественной групповой структурой и топологией равномерной сходимости на компактах (т. е. топологией, индуцированной компактно-открытой топологией на пространстве всех непрерывных функций из группе окружностей ), множество характеров Ĝ само является локально компактной абелевой группой, называемой двойственной к G Понтрягину группой . Для функции f из L 1 ( G ) его преобразование Фурье определяется формулой [16]
В этом случае справедлива лемма Римана–Лебега; f̂ ( ξ ) — функция, исчезающая на бесконечности на Ĝ .
Преобразование Фурье для T = R/Z является примером; здесь T — локально компактная абелева группа, а меру Хаара µ на T можно рассматривать как меру Лебега на [0,1). Рассмотрим представление T на комплексной плоскости C , которое представляет собой одномерное комплексное векторное пространство. Существует группа представлений (которые неприводимы, поскольку C 1-мерен) где для .
Характер такого представления, то есть след для каждого и , является сам. В случае представления конечной группы таблица характеров группы G представляет собой строки векторов, каждая из которых представляет собой характер одного неприводимого представления группы G , и эти векторы образуют ортонормированный базис пространства функций класса, которые отображаются из От G до C по лемме Шура. Теперь группа T уже не конечна, но все еще компактна и сохраняет ортонормированность таблицы характеров. Каждая строка таблицы представляет собой функцию из и внутренний продукт между двумя функциями класса (все функции являются функциями класса, поскольку T абелева) определяется как с нормирующим коэффициентом . Последовательность является ортонормированным базисом пространства функций класса .
Для любого представления V конечной G группы может быть выражено как интервал ( являются неповторяющимися группами G ), такие, что . Аналогично для и , . Двойник Понтрягина является и для , является его преобразованием Фурье для .
Преобразование Гельфанда [ править ]
Преобразование Фурье также является частным случаем преобразования Гельфанда . В этом конкретном контексте оно тесно связано с картой двойственности Понтрягина, определенной выше.
Дана абелева локально компактная хаусдорфова топологическая группа G , как и раньше, мы рассматриваем пространство L 1 ( G ) , определенный с помощью меры Хаара. При свертке как умножении L 1 ( G ) — абелева банахова алгебра . Он также имеет инволюцию *, заданную формулой
Дополнение по возможно наибольшей C * -норме дает ее обертывающую * -алгебру , называемую групповой C * -алгеброй C *( G ) группы G. C (любая C * -норма на L 1 ( G ) ограничен L 1 норма, следовательно, их супремум существует.)
Для любой абелевой С * -алгебры А преобразование Гельфанда дает изоморфизм между А и С0 А ( А ^) , где А ^ — мультипликативные линейные функционалы, т.е. одномерные представления на со слабой топологией. Карта просто дана
неабелевы Компактные группы
Преобразование Фурье также можно определить для функций неабелевой группы при условии, что группа компактна . Если исключить предположение о том, что основная группа абелева, неприводимые унитарные представления не всегда должны быть одномерными. Это означает, что преобразование Фурье в неабелевой группе принимает значения как операторы гильбертова пространства. [52] Преобразование Фурье компактных групп является основным инструментом теории представлений. [53] и некоммутативный гармонический анализ .
Пусть G — компактная Хаусдорфа топологическая группа . Обозначим через Σ совокупность всех классов изоморфизма конечномерных неприводимых унитарных представлений вместе с определенным выбором представления U ( п ) на гильбертовом пространстве H σ конечной размерности d σ для каждого σ ∈ Σ . Если µ — конечная борелевская мера на G , то преобразование Фурье–Стилтьеса µ — это оператор на H σ, определяемый формулой
Отображение
Верна теорема Петера -Вейля , и отсюда следует версия формулы обращения Фурье ( теорема Планшереля ): если f ∈ L 2 ( G ) , тогда
Обобщение преобразования Фурье на некоммутативную ситуацию также частично способствовало развитию некоммутативной геометрии . [ нужна ссылка ] В этом контексте категориальным обобщением преобразования Фурье на некоммутативные группы является двойственность Таннаки–Крейна , которая заменяет группу характеров категорией представлений. Однако при этом теряется связь с гармоническими функциями.
Альтернативы [ править ]
С точки зрения обработки сигналов , функция (времени) — это представление сигнала с идеальным временным разрешением , но без информации о частоте, в то время как преобразование Фурье имеет идеальное разрешение по частоте , но без информации о времени: величина преобразования Фурье в точке это то, сколько частотного содержания имеется, но местоположение задается только фазой (аргумент преобразования Фурье в точке), а стоячие волны не локализованы во времени - синусоидальная волна продолжается до бесконечности, не затухая. Это ограничивает полезность преобразования Фурье для анализа сигналов, локализованных во времени, особенно переходных процессов или любого сигнала конечной протяженности.
В качестве альтернативы преобразованию Фурье в частотно-временном анализе используются частотно-временные преобразования или частотно-временные распределения для представления сигналов в форме, которая содержит некоторую информацию о времени и некоторую информацию о частоте – в соответствии с принципом неопределенности существует компромисс. между ними. Это могут быть обобщения преобразования Фурье, такие как кратковременное преобразование Фурье , дробное преобразование Фурье , синхронно-сжатое преобразование Фурье, [54] или другие функции для представления сигналов, например, вейвлет-преобразования и лирплетные преобразования , причем вейвлет-аналог (непрерывного) преобразования Фурье является непрерывным вейвлет-преобразованием . [24]
Приложения [ править ]

Линейные операции, выполняемые в одной области (времени или частоте), имеют соответствующие операции в другой области, которые иногда легче выполнить. Операция дифференцирования во временной области соответствует умножению на частоту, [примечание 7] поэтому некоторые дифференциальные уравнения легче анализировать в частотной области. Кроме того, свертка во временной области соответствует обычному умножению в частотной области (см. Теорему о свертке ). После выполнения желаемых операций преобразование результата может быть произведено обратно во временную область. Гармонический анализ — это систематическое исследование взаимосвязи между частотной и временной областями, включая виды функций или операций, которые «проще» в той или иной области, и имеет глубокие связи со многими областями современной математики.
дифференциальных уравнений Анализ
Возможно, наиболее важным применением преобразования Фурье является решение уравнений в частных производных .Многие уравнения математической физики девятнадцатого века можно трактовать именно таким образом. Фурье изучил уравнение теплопроводности, которое в одном измерении и в безразмерных единицах имеет вид
Как обычно, проблема не в том, чтобы найти решение: их бесконечно много. Проблема заключается в так называемой «граничной задаче»: найти решение, удовлетворяющее «граничным условиям».
Здесь f и g — заданные функции. Для уравнения теплопроводности может потребоваться только одно граничное условие (обычно первое). Но для волнового уравнения по-прежнему существует бесконечно много решений y, удовлетворяющих первому граничному условию. Но когда накладываются оба условия, существует только одно возможное решение.
Легче найти преобразование Фурье ŷ решения, чем искать решение напрямую. Это связано с тем, что преобразование Фурье переводит дифференцирование в умножение на двойственную Фурье переменную, и поэтому уравнение в частных производных, примененное к исходной функции, преобразуется в умножение на полиномиальные функции двойственных переменных, примененных к преобразованной функции. После того, как ŷ определено, мы можем применить обратное преобразование Фурье, чтобы найти y .
Метод Фурье заключается в следующем. Прежде всего заметим, что любая функция форм
Во-вторых, заметим, что поэтому любой интеграл
Теперь это напоминает формулу синтеза Фурье функции. По сути, это действительное обратное преобразование Фурье a ± и b ± по переменной x .
Третий шаг — выяснить, как найти конкретные неизвестные коэффициентные функции a ± и b ± , которые приведут к тому, что y будет удовлетворять граничным условиям. Нас интересуют значения этих решений при t = 0 . Итак, мы установим t = 0 . Предполагая, что условия, необходимые для обращения Фурье, выполнены, мы можем затем найти синусные и косинусные преобразования Фурье (по переменной x ) обеих сторон и получить
Аналогично, взяв производную y по t и затем применив синусоидальные и косинусоидальные преобразования Фурье, получим
Это четыре линейных уравнения для четырех неизвестных a ± и b ± в терминах синус- и косинус-преобразований Фурье граничных условий, которые легко решаются с помощью элементарной алгебры, при условии, что эти преобразования могут быть найдены.
Таким образом, мы выбрали набор элементарных решений, параметризованных ξ , из которых общим решением была бы (непрерывная) линейная комбинация в виде интеграла по параметру ξ . Но этот интеграл имел форму интеграла Фурье. Следующим шагом было выразить граничные условия через эти интегралы и приравнять их к заданным функциям f и g . Но эти выражения также приняли форму интеграла Фурье из-за свойств преобразования Фурье производной. Последним шагом было использование инверсии Фурье путем применения преобразования Фурье к обеим сторонам, что позволило получить выражения для коэффициентных функций a ± и b ± в терминах заданных граничных условий f и g .
С более высокой точки зрения процедуру Фурье можно переформулировать более концептуально. Поскольку существует две переменные, мы будем использовать преобразование Фурье как для x, так и для t, а не действовать, как это делал Фурье, который преобразовывал только пространственные переменные. Обратите внимание, что ŷ необходимо рассматривать в смысле распределения, поскольку y ( x , t ) не будет L 1 : как волна, она будет сохраняться во времени и, следовательно, не является преходящим явлением. Но оно будет ограниченным, поэтому его преобразование Фурье можно определить как распределение. Операционные свойства преобразования Фурье, имеющие отношение к этому уравнению, заключаются в том, что оно преобразует дифференцирование по x в умножение на i 2π ξ , а дифференцирование по t — в умножение на i 2π f , где f — частота. Тогда волновое уравнение становится алгебраическим уравнением относительно ŷ :
Мы также можем рассматривать распределения, поддерживаемые на конике, которые задаются распределениями одной переменной на линии ξ = f плюс распределениями на линии ξ = - f следующим образом: если Φ — какая-либо пробная функция,
Тогда обращение Фурье дает для граничных условий нечто очень похожее на то, что мы имели более конкретно выше (положим Φ ( ξ , f ) = e я 2π( xξ + tf ) , который явно имеет полиномиальный рост):
Теперь, как и раньше, применение преобразования Фурье с одной переменной по переменной x к этим функциям x дает два уравнения в двух неизвестных распределениях s ± (которые можно считать обычными функциями, если граничные условия L 1 или Л 2 ).
С вычислительной точки зрения недостатком, конечно, является то, что нужно сначала вычислить преобразования Фурье граничных условий, затем собрать из них решение, а затем вычислить обратное преобразование Фурье. Формулы в закрытой форме встречаются редко, за исключением случаев, когда существует некоторая геометрическая симметрия, которую можно использовать, а численные расчеты затруднены из-за колебательного характера интегралов, что делает сходимость медленной и трудно поддающейся оценке. Для практических расчетов часто используют другие методы.
В двадцатом веке эти методы были распространены на все линейные уравнения в частных производных с полиномиальными коэффициентами, а за счет расширения понятия преобразования Фурье, включив в него интегральные операторы Фурье, а также некоторые нелинейные уравнения.
Фурье преобразованием с Спектроскопия
Преобразование Фурье также используется в ядерном магнитном резонансе (ЯМР) и других видах спектроскопии , например, инфракрасной ( FTIR ). В ЯМР сигнал затухания свободной индукции (FID) экспоненциальной формы регистрируется во временной области и преобразуется Фурье в лоренцеву форму линии в частотной области. Преобразование Фурье также используется в магнитно-резонансной томографии (МРТ) и масс-спектрометрии .
Квантовая механика [ править ]
Преобразование Фурье полезно в квантовой механике по крайней мере двумя разными способами. Начнем с того, что основная концептуальная структура квантовой механики постулирует существование пар дополнительных переменных , связанных принципом неопределенности Гейзенберга . Например, в одном измерении пространственная переменная q , скажем, частицы, может быть измерена только с помощью квантовомеханического « оператора положения » ценой потери информации об импульсе p частицы. Следовательно, физическое состояние частицы может быть описано либо функцией q , называемой «волновой функцией», либо функцией p , но не функцией обеих переменных. Переменная p называется переменной, сопряженной с q . В классической механике физическое состояние частицы (существующей в одном измерении, для простоты изложения) будет задано путем одновременного присвоения определенных значений как p , так и q . Таким образом, совокупность всех возможных физических состояний представляет собой двумерное вещественное векторное пространство с осью p и Ось q называется фазовым пространством .
Напротив, квантовая механика выбирает поляризацию этого пространства в том смысле, что она выбирает подпространство размером в половину измерения, например, только ось q , но вместо того, чтобы рассматривать только точки, берет набор всех комплексных значений. «волновые функции» на этой оси. Тем не менее, выбор оси p является столь же допустимой поляризацией, приводящей к другому представлению набора возможных физических состояний частицы. Оба представления волновой функции связаны преобразованием Фурье, так что
Физически реализуемые состояния — это L 2 , и поэтому по теореме Планшереля их преобразования Фурье также L 2 . (Обратите внимание, что, поскольку q выражено в единицах расстояния, а p — в единицах импульса, наличие постоянной Планка в показателе степени делает показатель степени безразмерным , как и должно быть.)
Следовательно, преобразование Фурье можно использовать для перехода от одного способа представления состояния частицы с помощью волновой функции положения к другому способу представления состояния частицы: с помощью волновой функции импульса. Возможно бесконечно много различных поляризаций, и все они одинаково действительны. Возможность преобразовывать состояния из одного представления в другое с помощью преобразования Фурье не только удобна, но и является основной причиной принципа неопределенности Гейзенберга .
Другое применение преобразования Фурье как в квантовой механике, так и в квантовой теории поля — решение применимого волнового уравнения. В нерелятивистской квантовой механике уравнение Шредингера для изменяющейся во времени волновой функции в одном измерении, не подверженной воздействию внешних сил, имеет вид
Это то же самое, что и уравнение теплопроводности, за исключением присутствия мнимой единицы i . Для решения этого уравнения можно использовать методы Фурье.
При наличии потенциала, заданного функцией потенциальной энергии V ( x ) , уравнение принимает вид
«Элементарные решения», как мы называли их выше, представляют собой так называемые «стационарные состояния» частицы, и алгоритм Фурье, описанный выше, все еще можно использовать для решения краевой задачи будущей эволюции ψ учитывая его значения для t = 0 . Ни один из этих подходов не имеет большого практического применения в квантовой механике. Краевые задачи и эволюция волновой функции во времени не представляют большого практического интереса: наиболее важны стационарные состояния.
В релятивистской квантовой механике уравнение Шредингера становится волновым уравнением, как это было обычно в классической физике, за исключением того, что рассматриваются комплексные волны. Простым примером при отсутствии взаимодействия с другими частицами или полями является свободное одномерное уравнение Клейна – Гордона – Шредингера – Фока, на этот раз в безразмерных единицах:
С математической точки зрения это то же самое, что и решенное выше волновое уравнение классической физики (но с комплексной волной, что не имеет никакого значения в методах). Это очень полезно в квантовой теории поля: каждый отдельный компонент Фурье волны можно рассматривать как отдельный гармонический осциллятор, а затем квантовать - процедура, известная как «второе квантование». Методы Фурье были адаптированы и для решения нетривиальных взаимодействий.
Наконец, числовой оператор квантового гармонического осциллятора можно интерпретировать, например, через ядро Мелера , как генератор Фурье преобразования . [27]
Обработка сигналов [ править ]
Преобразование Фурье используется для спектрального анализа временных рядов. Однако при статистической обработке сигналов преобразование Фурье обычно не применяется к самому сигналу. Даже если реальный сигнал действительно является нестационарным, на практике оказалось целесообразным моделировать сигнал функцией (или, альтернативно, случайным процессом), которая является стационарной в том смысле, что ее характерные свойства постоянны во все времена. Преобразование Фурье такой функции не существует в обычном смысле этого слова, и для анализа сигналов было сочтено более полезным вместо этого использовать преобразование Фурье ее автокорреляционной функции.
Автокорреляционная функция R функции f определяется формулой
Эта функция является функцией временной задержки τ, проходящей между значениями f, подлежащими корреляции.
Для большинства функций f , встречающихся на практике, R является ограниченной четной функцией запаздывания τ и для типичных зашумленных сигналов оказывается равномерно непрерывной с максимумом при τ = 0 .
Функция автокорреляции, более правильно называемая функцией автоковариации, если она не нормализована каким-либо подходящим образом, измеряет силу корреляции между значениями f, разделенными временной задержкой. Это способ поиска связи f с собственным прошлым. Это полезно даже для других статистических задач, помимо анализа сигналов. Например, если f ( t ) представляет температуру в момент времени t , можно ожидать сильной корреляции с температурой с задержкой в 24 часа.
Он обладает преобразованием Фурье,
Это преобразование Фурье называется спектральной плотности мощности функцией f . не отфильтровать все периодические компоненты (Если сначала из f , этот интеграл будет расходиться, но такие периодичности легко отфильтровать.)
Спектр мощности, как указано этой функцией плотности P , измеряет величину дисперсии, вносимой в данные частотой ξ . В электрических сигналах дисперсия пропорциональна средней мощности (энергии в единицу времени), поэтому спектр мощности описывает, какой вклад различные частоты вносят в среднюю мощность сигнала. Этот процесс называется спектральным анализом временных рядов и аналогичен обычному дисперсионному анализу данных, не являющихся временными рядами ( ANOVA ).
Знание того, какие частоты «важны» в этом смысле, имеет решающее значение для правильной разработки фильтров и правильной оценки измерительных приборов. Это также может быть полезно для научного анализа явлений, ответственных за получение данных.
Спектр мощности сигнала также можно приблизительно измерить непосредственно путем измерения средней мощности, которая остается в сигнале после того, как все частоты за пределами узкой полосы были отфильтрованы.
Спектральный анализ проводится и для визуальных сигналов. Спектр мощности игнорирует все фазовые соотношения, что достаточно хорошо для многих целей, но для видеосигналов также необходимо использовать другие типы спектрального анализа, по-прежнему используя преобразование Фурье в качестве инструмента.
Другие обозначения [ править ]
Другие распространенные обозначения для включать:
В науке и технике также часто делаются такие замены:
Итак, пара преобразований может стать
Недостаток записи заглавных букв заключается в том, что при выражении преобразования, такого как или что становится еще более неловким и
В некоторых контекстах, таких как физика элементарных частиц, тот же символ может использоваться как для функции, так и для преобразования Фурье, причем эти два параметра различаются только своим аргументом Ie будет относиться к преобразованию Фурье из-за аргумента импульса, в то время как будет ссылаться на исходную функцию из-за позиционного аргумента. Хотя тильды могут использоваться, как в для обозначения преобразований Фурье тильды также могут использоваться для обозначения модификации величины с более лоренц-инвариантной формой, например: , поэтому следует соблюдать осторожность. Сходным образом, часто обозначает Гильберта преобразование .
Интерпретации комплексной функции f̂ ( ξ ) можно помочь, выразив ее в полярных координат. форме
Тогда обратное преобразование можно записать:
Преобразование Фурье можно рассматривать как отображение функциональных пространств. Это отображение здесь обозначается F , а F ( f ) используется для обозначения преобразования Фурье функции f . Это отображение является линейным, что означает, что F также можно рассматривать как линейное преобразование в функциональном пространстве, и подразумевает, что стандартные обозначения в линейной алгебре применения линейного преобразования к вектору (здесь функция f ) могут использоваться для записи F ж вместо F ( ж ) . Поскольку результатом применения преобразования Фурье снова является функция, нас может интересовать значение этой функции, оцененное по значению ξ для ее переменной, и это обозначается либо как F f ( ξ ) , либо как ( F f )( ξ ) . Обратите внимание, что в первом случае неявно подразумевается, что F сначала применяется к f , а затем результирующая функция оценивается в ξ , а не наоборот.
В математике и различных прикладных науках часто необходимо различать функцию f и значение f, когда ее переменная равна x , обозначаемая f ( x ) . Это означает, что обозначение типа F ( f ( x )) формально можно интерпретировать как преобразование Фурье значений f в точке x . Несмотря на этот недостаток, предыдущее обозначение встречается часто, часто, когда необходимо преобразовать конкретную функцию или функцию определенной переменной. Например,
что преобразованная функция является функцией от x , а не от x0 Обратите внимание: последний пример верен только в предположении , .
Как обсуждалось выше, характеристическая функция случайной величины такая же, как преобразование Фурье – Стилтьеса ее меры распределения, но в этом контексте типично принять другое соглашение для констант. Обычно характеристическая функция определяется
Как и в случае с соглашением о «неунитарной угловой частоте», приведенном выше, коэффициент 2 π не появляется ни в нормирующей константе, ни в показателе степени. В отличие от любого из соглашений, упомянутых выше, это соглашение принимает противоположный знак в показателе степени.
Методы расчета [ править ]
Соответствующий метод вычисления во многом зависит от того, как представлена исходная математическая функция, и от желаемой формы выходной функции. В этом разделе мы рассматриваем обе функции непрерывной переменной: и функции дискретной переменной (т.е. упорядоченные пары и ценности). Для дискретных интеграл преобразования становится суммой синусоид, которая по-прежнему является непрерывной функцией частоты ( или ). Когда синусоиды гармонически связаны (т.е. когда -значения располагаются с интервалом в целое число, кратное интервалу), преобразование называется преобразованием Фурье с дискретным временем (DTFT).
Дискретные преобразования Фурье и преобразования быстрые Фурье
Выборка DTFT при равноотстоящих друг от друга значениях частоты является наиболее распространенным современным методом вычислений. Эффективные процедуры, в зависимости от необходимого разрешения по частоте, описаны в разделе Дискретное преобразование Фурье § Выборка DTFT . Используемое там дискретное преобразование Фурье (ДПФ) обычно вычисляется с помощью алгоритма быстрого преобразования Фурье (БПФ).
Аналитическая интеграция функций закрытой формы [ править ]
Таблицы преобразований Фурье в замкнутой форме , такие как § Функции, интегрируемые с квадратом, одномерные и § Таблица преобразований Фурье в дискретном времени , создаются путем математической оценки интеграла анализа Фурье (или суммирования) в другую функцию частоты в замкнутой форме. ( или ). [55] Если это математически возможно, это обеспечивает преобразование континуума значений частоты.
Многие системы компьютерной алгебры, такие как Matlab и Mathematica , способные к символьному интегрированию , способны аналитически вычислять преобразования Фурье. Например, чтобы вычислить преобразование Фурье cos(6π t ) e −π т 2 можно ввести команду integrate cos(6*pi*t) exp(−pi*t^2) exp(-i*2*pi*f*t) from -inf to inf в Вольфрам Альфа . [примечание 8]
замкнутой формы непрерывных функций интегрирование Численное
Дискретная выборка преобразования Фурье также может быть выполнена путем численного интегрирования определения при каждом значении частоты, для которой требуется преобразование. [56] [57] [58] Подход численного интегрирования работает с гораздо более широким классом функций, чем аналитический подход.
ряда упорядоченных пар интегрирование Численное
Если входная функция представляет собой серию упорядоченных пар, численное интегрирование сводится к простому суммированию по набору пар данных. [59] DTFT является распространенным подслучаем этой более общей ситуации.
Таблицы преобразований важных Фурье
В следующих таблицах записаны некоторые преобразования Фурье в закрытой форме. Для функций f ( x ) и g ( x ) обозначайте их преобразования Фурье через f̂ и ĝ . Включены только три наиболее распространенных соглашения. Может быть полезно заметить, что запись 105 дает связь между преобразованием Фурье функции и исходной функцией, которую можно рассматривать как связь преобразования Фурье и его обратного.
Функциональные отношения, одномерные [ править ]
Преобразования Фурье в этой таблице можно найти у Эрдели (1954) или Каммлера (2000 , приложение).
| Функция | Преобразование Фурье унитарная, обычная частота | Преобразование Фурье унитарная, угловая частота | Преобразование Фурье неунитарная, угловая частота | Примечания | |
|---|---|---|---|---|---|
| Определения | |||||
| 101 | Линейность | ||||
| 102 | Сдвиг во временной области | ||||
| 103 | Сдвиг в частотной области, двойной 102 | ||||
| 104 | Масштабирование во временной области. Если | а | велико, то f ( ax ) концентрируется около 0 и растекается и выравнивается. | ||||
| 105 | Одно и то же преобразование применяется дважды, но x заменяет частотную переменную ( ξ или ω ) после первого преобразования. | ||||
| 106 | н й -порядковая производная. Поскольку f — функция Шварца | ||||
| 106.5 | Интеграция. [60] Примечание: - дельта-функция Дирака и среднее ( DC ) значение такой, что | ||||
| 107 | Это двойник 106. | ||||
| 108 | Обозначение f ∗ g обозначает свертку f свертке и g — это правило представляет собой теорему о | ||||
| 109 | Это двойник 108. | ||||
| 110 | Для f ( x ) чисто вещественный | Эрмитова симметрия. z указывает на комплексно-сопряженное число . | |||
| 113 | Для f ( x ) чисто мнимая | z указывает на комплексно-сопряженное число . | |||
| 114 | Комплексное сопряжение , обобщение 110 и 113 | ||||
| 115 | Это следует из правил 101 и 103 с использованием формулы Эйлера : | ||||
| 116 | Это следует из 101 и 103 по формуле Эйлера : |
Квадратно-интегрируемые функции, одномерные [ править ]
Преобразования Фурье в этой таблице можно найти у Кэмпбелла и Фостера (1948) , Эрдели (1954) или Каммлера (2000 , приложение).
| Функция | Преобразование Фурье унитарная, обычная частота | Преобразование Фурье унитарная, угловая частота | Преобразование Фурье неунитарная, угловая частота | Примечания | |
|---|---|---|---|---|---|
| Определения | |||||
| 201 | Прямоугольный импульс и нормализованная функция sinc , определяемая здесь как sinc( x ) = грех(π x ) / π x | ||||
| 202 | Двойное правило 201. Прямоугольная функция представляет собой идеальный фильтр нижних частот , а функция sinc — это непричинная импульсная характеристика такого фильтра. Функция sinc здесь определяется как sinc( x ) = грех(π x ) / π x | ||||
| 203 | Функция tri( x ) является треугольной функцией | ||||
| 204 | Двойное правило 203. | ||||
| 205 | Функция u ( x ) является единичной ступенчатой функцией Хевисайда и a > 0 . | ||||
| 206 | Это показывает, что для унитарных преобразований Фурье функция Гаусса e − αx 2 является собственным преобразованием Фурье для некоторого выбора α . Чтобы это было интегрируемо, мы должны иметь Re( α ) > 0 . | ||||
| 208 | Для Re( a ) > 0 . То есть преобразование Фурье двусторонней убывающей показательной функции является функцией Лоренца . | ||||
| 209 | Гиперболический секанс представляет собой собственное преобразование Фурье. | ||||
| 210 | H n — n -го порядка полином Эрмита . Если a = 1 , то функции Гаусса–Эрмита являются собственными функциями оператора преобразования Фурье. Для вывода см. Полином Эрмита . Формула сводится к 206 для n = 0 . |
Распределения одномерные [ править ]
Преобразования Фурье в этой таблице можно найти у Эрдели (1954) или Каммлера (2000 , приложение).
| Функция | Преобразование Фурье унитарная, обычная частота | Преобразование Фурье унитарная, угловая частота | Преобразование Фурье неунитарная, угловая частота | Примечания | |
|---|---|---|---|---|---|
| Определения | |||||
| 301 | Распределение δ ( ξ ) обозначает дельта-функцию Дирака . | ||||
| 302 | Двойное правило 301. | ||||
| 303 | Это следует из 103 и 301. | ||||
| 304 | Это следует из правил 101 и 303 с использованием формулы Эйлера : | ||||
| 305 | Это следует из 101 и 303 с использованием | ||||
| 306 | Это следует из 101 и 207 с использованием | ||||
| 307 | Это следует из 101 и 207 с использованием | ||||
| 308 | Здесь предполагается реально. В случае, когда альфа является комплексной, см. запись 206 таблицы выше. | ||||
| 309 | Здесь n — натуральное число , а δ ( н ) ( ξ ) — n- я производная распределения дельта-функции Дирака. Это правило следует из правил 107 и 301. Объединив это правило с правилом 101, мы можем преобразовать все многочлены . | ||||
| 310 | Двойственно правилу 309. δ ( н ) ( ξ ) — n- я производная распределения дельта-функции Дирака. Это правило следует из 106 и 302. | ||||
| 311 | Здесь sn( ξ ) – знаковая функция . Обратите внимание, что 1 / x не является распределением. необходимо использовать главное значение Коши При тестировании функций Шварца . Это правило полезно при изучении преобразования Гильберта . | ||||
| 312 | 1 / х н - однородное распределение, определяемое производной распределения | ||||
| 313 | Эта формула справедлива для 0 > α > −1 . При α > 0 в начале координат возникают сингулярные члены, которые можно найти, дифференцируя 320. Если Re α > −1 , то | х | а является локально интегрируемой функцией и, следовательно, умеренным распределением. Функция α ↦ | х | а — голоморфная функция из правой полуплоскости в пространство умеренных распределений. Он допускает уникальное мероморфное расширение до умеренного распределения, также обозначаемого | х | а для α ≠ −1, −3, ... (См. однородное распределение .) | ||||
| Особый случай 313. | |||||
| 314 | Двойственно правилу 311. На этот раз преобразования Фурье необходимо рассматривать как главное значение Коши . | ||||
| 315 | Функция u ( x ) Хевисайда является единичной ступенчатой функцией ; это следует из правил 101, 301 и 314. | ||||
| 316 | Эта функция известна как функция гребенки Дирака . Этот результат можно получить из 302 и 102, а также того факта, что в качестве раздач. | ||||
| 317 | Функция J 0 ( x ) нулевого порядка является функцией Бесселя первого рода. | ||||
| 318 | Это обобщение 317. Функция J n ( x ) является n- го порядка функцией Бесселя первого рода. Функция Tn представляет ( x ) собой полином Чебышева первого рода . | ||||
| 319 | γ — постоянная Эйлера–Машерони . При тестировании необходимо использовать интеграл конечной части. 1 / | ξ | или 1 / | ω | против функций Шварца . Детали этого могут изменить коэффициент дельта-функции. | ||||
| 320 | Эта формула справедлива для 1 > α > 0 . Используйте дифференцирование, чтобы вывести формулу для более высоких показателей. u — функция Хевисайда. |
Двумерные функции [ править ]
| Функция | Преобразование Фурье унитарная, обычная частота | Преобразование Фурье унитарная, угловая частота | Преобразование Фурье неунитарная, угловая частота | Примечания | |
|---|---|---|---|---|---|
| 400 | Переменные ξ x , ξ y , ω x , ω y являются действительными числами. Интегралы берутся по всей плоскости. | ||||
| 401 | Обе функции являются гауссовыми и могут не иметь единичного объема. | ||||
| 402 | Функция определяется как circ( r ) = 1 для 0 ≤ r ≤ 1 и равна 0 в противном случае. Результатом является распределение амплитуды диска Эйри и выражается через J 1 первого порядка ). ( функция Бесселя первого рода [61] | ||||
| 403 | Это Ханкеля преобразование r −1 , двумерное «самопреобразование» Фурье. [62] | ||||
| 404 |
Формулы для общих n -мерных функций [ править ]
| Функция | Преобразование Фурье унитарная, обычная частота | Преобразование Фурье унитарная, угловая частота | Преобразование Фурье неунитарная, угловая частота | Примечания | |
|---|---|---|---|---|---|
| 500 | |||||
| 501 | Функция χ [0,1] является индикаторной функцией интервала [0,1] . Функция Γ( x ) является гамма-функцией. Функция J n / 2 + δ — функция Бесселя первого рода, порядка п / 2 + δ . Взяв n = 2 и δ = 0, получим 402. [63] | ||||
| 502 | См. потенциал Рисса , где константа определяется выражением Формула также справедлива для всех α ≠ n , n + 2, ... посредством аналитического продолжения, но тогда функцию и ее преобразования Фурье необходимо понимать как соответствующим образом регуляризованные умеренные распределения. См. однородное распределение . [примечание 9] | ||||
| 503 | Это формула многомерного нормального распределения, нормализованного к 1 со средним значением 0. Переменные, выделенные жирным шрифтом, представляют собой векторы или матрицы. Следуя обозначениям на вышеупомянутой странице, Σ = σ σ Т и Σ −1 = п −Т п −1 | ||||
| 504 | Здесь [64] Re( α ) > 0 |
См. также [ править ]
- Аналоговая обработка сигналов
- Полоса Биверса – Липсона
- Преобразование с постоянной Q
- Дискретное преобразование Фурье
- * Матрица ДПФ
- Быстрое преобразование Фурье
- Интегральный оператор Фурье
- Теорема обращения Фурье
- Множитель Фурье
- ряд Фурье
- Синусоидальное преобразование Фурье
- Преобразование Фурье – Делиня
- Преобразование Фурье – Мукая
- Дробное преобразование Фурье
- Косвенное преобразование Фурье
- Интегральное преобразование
- Преобразование Лапласа
- Спектральный анализ методом наименьших квадратов
- Линейное каноническое преобразование
- Средняя трансформация
- Многомерное преобразование
- NGC 4622 , особенно изображение NGC 4622 с преобразованием Фурье m = 2 .
- Нелокальный оператор
- Квантовое преобразование Фурье
- Квадратичное преобразование Фурье
- Кратковременное преобразование Фурье
- Спектральная плотность
- Символическая интеграция
- Дисперсионное преобразование Фурье с растяжением во времени
- Преобразование (математика)
Примечания [ править ]
- ^ В зависимости от применения Лебега . наиболее подходящим может быть интегральный , распределительный или другой подход
- ^ Вретблад (2000) дает убедительное обоснование этих формальных процедур, не вдаваясь слишком глубоко в функциональный анализ или теорию распределений .
- ^ В релятивистской квантовой механике встречаются векторные преобразования Фурье многокомпонентных волновых функций. В квантовой теории поля часто используются операторные преобразования Фурье операторных функций пространства-времени, см., например, Greiner & Reinhardt (1996) .
- ^ В этой статье быстро убывающая функция — это функция на вещественных числах, стремящихся к нулю вместе со всеми производными как : . См. функцию Шварца .
- ^ Возможный источник путаницы — свойство сдвига частоты ; т.е. преобразование функции является Значение этой функции в является означает, что частота было сдвинуто к нулю (см. также Отрицательная частота ).
- ^ Оператор определяется заменой к в Тейлора разложении
- ^ С точностью до мнимого постоянного коэффициента, величина которого зависит от того, какое преобразование Фурье используется.
- ^ Прямая команда
fourier transform of cos(6*pi*t) exp(−pi*t^2)также будет работать для Wolfram Alpha, хотя параметры соглашения (см. Преобразование Фурье § Другие соглашения ) должны быть изменены по сравнению с параметром по умолчанию, который фактически эквивалентенintegrate cos(6*pi*t) exp(−pi*t^2) exp(i*omega*t) /sqrt(2*pi) from -inf to inf. - ^ В Гельфанде и Шилове 1964 , с. 363, с неунитарными соглашениями этой таблицы, преобразование дано быть
откуда это следует, причем .
Цитаты [ править ]
- ^ Кхаре, Бутола и Раджора, 2023 , стр. 13–14.
- ^ Кайзер 1994 , с. 29
- ^ Рахман 2011 , с. 11
- ^ Дим и Маккин, 1985 г.
- ^ Фурье 1822 , с. 525
- ^ Фурье 1878 , с. 408
- ^ Джордан (1883) доказывает на стр. 216–226 интегральную теорему Фурье перед изучением рядов Фурье.
- ^ Титчмарш 1986 , с. 1
- ^ Рахман 2011 , с. 10.
- ^ Оппенгейм, Шафер и Бак 1999 , стр. 58
- ^ Jump up to: Перейти обратно: а б с д и ж г Штейн и Вайс 1971 г.
- ^ Фолланд 1989
- ^ Фурье 1822 г.
- ^ Jump up to: Перейти обратно: а б с д и Пинский 2002 г.
- ^ Арфкен 1985
- ^ Jump up to: Перейти обратно: а б с д и Кацнельсон 1976 г.
- ^ Рудин 1987 , с. 187
- ^ Рудин 1987 , с. 186
- ^ Фолланд 1992 , стр. 216.
- ^ Вольф 1979 , с. 307ff
- ^ Фолланд 1989 , стр. 53.
- ^ Челегини, Гаделла и дель Ольмо, 2021 г.
- ^ Jump up to: Перейти обратно: а б Дуоандикоэчеа 2001
- ^ Jump up to: Перейти обратно: а б Боашаш 2003 г.
- ^ Кондон 1937 г.
- ^ Вольф 1979 , с. 320
- ^ Jump up to: Перейти обратно: а б Вольф 1979 , с. 312
- ^ Фолланд 1989 , стр. 52.
- ^ Хоу 1980
- ^ Пейли и Винер, 1934 г.
- ^ Гельфанд и Виленкин, 1964 г.
- ^ Kirillov & Gvishiani 1982
- ^ Клозель и Делорм 1985 , стр. 331–333.
- ^ де Гроот и Мазур 1984 , с. 146
- ^ Чампни 1987 , с. 80
- ^ Jump up to: Перейти обратно: а б с Kolmogorov & Fomin 1999
- ^ Винер 1949 г.
- ^ Чампни 1987 , с. 63
- ^ Виддер и Винер 1938 , с. 537
- ^ Пинский 2002 , с. 131
- ^ Штейн и Шакарчи, 2003 г.
- ^ Штейн и Шакарчи 2003 , с. 158
- ^ Чатфилд 2004 , с. 113
- ^ Фурье 1822 , с. 441
- ^ Пуанкаре 1895 , с. 102
- ^ Уиттакер и Уотсон 1927 , с. 188
- ^ Графакас 2004 г.
- ^ Графакос и Тешль, 2013 г.
- ^ «Прикладной анализ Фурье и элементы современной обработки сигналов, лекция 3» (PDF) . 12 января 2016 года . Проверено 11 октября 2019 г.
- ^ Штейн и Вайс 1971 , Thm. 2.3
- ^ Пинский 2002 , с. 256
- ^ Хьюитт и Росс 1970 , Глава 8
- ^ Почти 2001 г.
- ^ Коррейя, Л.Б.; Хусто, Дж. Ф.; Анжелико, бакалавр (2024 г.). «Полиномиальное адаптивное синхронно-сжатое преобразование Фурье: метод оптимизации мультиразрешения». Цифровая обработка сигналов . 150 : 104526. doi : 10.1016/j.dsp.2024.104526 .
- ^ Выпускник и др. 2015 год
- ^ Пресс и др. 1992 год
- ^ Бэйли и Шварцтраубер, 1994 г.
- ^ Сторона 1971 г.
- ^ Симонен и Олкконен, 1985 г.
- ^ «Свойство интегрирования преобразования Фурье» . Преобразование Фурье.com . 2015 [2010]. Архивировано из оригинала 26 января 2022 г. Проверено 20 августа 2023 г.
- ^ Штейн и Вайс 1971 , Thm. IV.3.3
- ^ Истон 2010
- ^ Штейн и Вайс 1971 , Thm. 4.15
- ^ Штейн и Вайс 1971 , с. 6
Ссылки [ править ]
- Арфкен, Джордж (1985), Математические методы для физиков (3-е изд.), Academic Press, ISBN 9780120598205
- Бейли, Дэвид Х.; Шварцтраубер, Пол Н. (1994), «Быстрый метод численной оценки непрерывных преобразований Фурье и Лапласа» (PDF) , SIAM Journal on Scientific Computing , 15 (5): 1105–1110, Бибкод : 1994SJSC...15.1105 B , CiteSeerX 10.1.1.127.1534 , doi : 10.1137/0915067 , заархивировано из оригинала (PDF) 20 июля 2008 г. , получено 1 ноября 2017 г.
- Боашаш, Б., изд. (2003), Частотно-временной анализ и обработка сигналов: полный справочник , Оксфорд: Elsevier Science, ISBN 978-0-08-044335-5
- Бохнер, С .; Чандрасекхаран, К. (1949), Преобразования Фурье , Princeton University Press
- Брейсвелл, Р.Н. (2000), Преобразование Фурье и его приложения (3-е изд.), Бостон: McGraw-Hill, ISBN 978-0-07-116043-8
- Кэмпбелл, Джордж; Фостер, Рональд (1948), Интегралы Фурье для практических приложений , Нью-Йорк: D. Van Nostand Company, Inc.
- Челегини, Энрико; Гаделла, Мануэль; дель Ольмо, Мариано А. (2021), «Функции Эрмита и ряды Фурье», Symmetry , 13 (5): 853, arXiv : 2007.10406 , Bibcode : 2021Symm...13..853C , doi : 10.3390/sym13050853
- Чампени, округ Колумбия (1987), Справочник по теоремам Фурье , издательство Кембриджского университета.
- Чатфилд, Крис (2004), Анализ временных рядов: введение , Тексты по статистическим наукам (6-е изд.), Лондон: Chapman & Hall/CRC, ISBN 9780203491683
- Клозель, Лоран; Делорм, Патрис (1985), «Об инвариантной теореме Пэли-Винера для вещественных редуктивных групп Ли», Comptes Rendus de l'Académie des Sciences, Série I , 300 : 331–333
- Кондон, ЕС (1937), «Погружение преобразования Фурье в непрерывную группу функциональных преобразований», Proc. Натл. акад. наук. , 23 (3): 158–164, Бибкод : 1937PNAS...23..158C , doi : 10.1073/pnas.23.3.158 , PMC 1076889 , PMID 16588141
- де Гроот, Сибрен Р.; Мазур, Питер (1984), Неравновесная термодинамика (2-е изд.), Нью-Йорк: Дувр .
- Дуоандикоэчеа, Хавьер (2001), Анализ Фурье , Американское математическое общество , ISBN 978-0-8218-2172-5
- Дым, Х. ; Маккин, Х. (1985), Ряды Фурье и интегралы , Academic Press , ISBN 978-0-12-226451-1
- Истон, Роджер Л. младший (2010), Методы Фурье в визуализации , John Wiley & Sons, ISBN 978-0-470-68983-7 , получено 26 мая 2020 г.
- Эрдели, Артур, изд. (1954), Таблицы интегральных преобразований , вып. 1, МакГроу-Хилл
- Феллер, Уильям (1971), Введение в теорию вероятностей и ее приложения , том. II (2-е изд.), Нью-Йорк: Wiley , MR 0270403.
- Фолланд, Джеральд (1989), Гармонический анализ в фазовом пространстве , Princeton University Press
- Фолланд, Джеральд (1992), Анализ Фурье и его приложения , Wadsworth & Brooks/Cole.
- Фурье, Ж. Б. Жозеф (1822), Аналитическая теория тепла (на французском языке), Париж: Фирмин Дидо, отец и сын, OCLC 2688081
- Фурье, Ж. Б. Жозеф (1878) [1822], Аналитическая теория тепла , перевод Александра Фримена, The University Press (перевод с французского)
- Градштейн Израиль Соломонович ; Рыжик Иосиф Моисеевич ; Героним Юрий Вениаминович ; Цейтлин Михаил Юльевич ; Джеффри, Алан (2015), Цвиллингер, Дэниел; Молл, Виктор Гюго (ред.), Таблица интегралов, рядов и произведений , перевод Scripta Technica, Inc. (8-е изд.), Academic Press , ISBN 978-0-12-384933-5
- Графакос, Лукас (2004), Классический и современный анализ Фурье , Прентис-Холл, ISBN 978-0-13-035399-3
- Графакос, Лукас; Тешль, Джеральд (2013), «О преобразованиях Фурье радиальных функций и распределений», J. Fourier Anal. Прил. , 19 : 167–179, arXiv : 1112.5469 , doi : 10.1007/s00041-012-9242-5 , S2CID 1280745
- Грейнер, В.; Рейнхардт, Дж. (1996), Квантование поля , Springer , ISBN 978-3-540-59179-5
- Гельфанд, ИМ ; Шилов Г.Е. (1964), Обобщенные функции , вып. 1, Нью-Йорк: Академик Пресс (перевод с русского)
- Гельфанд, ИМ ; Виленкин, Нью-Йорк (1964), Обобщенные функции , вып. 4, Нью-Йорк: Академик Пресс (перевод с русского)
- Хьюитт, Эдвин; Росс, Кеннет А. (1970), Абстрактный гармонический анализ , Основы математических наук, том 152, том. II: Структура и анализ компактных групп. Анализ локально компактных абелевых групп, Springer , MR 0262773.
- Хёрмандер, Л. (1976), Линейные операторы с частными производными , вып. 1, Спрингер , ISBN 978-3-540-00662-6
- Хоу, Роджер (1980), «О роли группы Гейзенберга в гармоническом анализе», Бюллетень Американского математического общества , 3 (2): 821–844, doi : 10.1090/S0273-0979-1980-14825-9 , МР 0578375
- Джеймс, Дж. Ф. (2011), Руководство для студентов по преобразованиям Фурье (3-е изд.), Cambridge University Press , ISBN 978-0-521-17683-5
- Джордан, Камилла (1883), Cours d'Analyse de l'École Polytechnique , vol. II, Интегральное исчисление: определенные и неопределенные интегралы (2-е изд.), Париж.
{{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - Кайзер, Джеральд (1994), «Дружественное руководство по вейвлетам» , Physics Today , 48 (7): 57–58, Bibcode : 1995PhT....48g..57K , doi : 10.1063/1.2808105 , ISBN 978-0-8176-3711-8
- Каммлер, Дэвид (2000), Первый курс анализа Фурье , Прентис Холл, ISBN 978-0-13-578782-3
- Кацнельсон, Ицхак (1976), Введение в гармонический анализ , Дувр , ISBN 978-0-486-63331-2
- Харе, Кедар; Бутола, манси; Раджора, Сунаина (2023), «Глава 2.3 Преобразование Фурье как предельный случай ряда Фурье», Оптика Фурье и вычислительная обработка изображений (2-е изд.), Springer, doi : 10.1007/978-3-031-18353-9 , ISBN 978-3-031-18353-9 , S2CID 255676773
- Кириллов Александр ; Гвишиани, Алексей Д. (1982) [1979], Теоремы и проблемы функционального анализа , Спрингер (перевод с русского)
- Кнапп, Энтони В. (2001), Теория представлений полупростых групп: обзор, основанный на примерах , Princeton University Press , ISBN 978-0-691-09089-4
- Колмогоров Андрей Николаевич ; Фомин, Сергей Васильевич (1999) [1957], Элементы теории функций и функционального анализа , Дувр (перевод с русского)
- Ладо, Ф. (1971), «Численные преобразования Фурье в одном, двух и трех измерениях для расчетов в жидком состоянии» , Журнал вычислительной физики , 8 (3): 417–433, Бибкод : 1971JCoPh...8..417L , дои : 10.1016/0021-9991(71)90021-0
- Мюллер, Мейнард (2015), Преобразование Фурье в двух словах. (PDF) , Спрингер , номер документа : 10.1007/978-3-319-21945-5 , ISBN 978-3-319-21944-8 , S2CID 8691186 , заархивировано из оригинала (PDF) 8 апреля 2016 г. , получено 28 марта 2016 г .; также доступно в разделе «Основы обработки музыки» , раздел 2.1, страницы 40–56.
- Оппенгейм, Алан В .; Шафер, Рональд В .; Бак, Джон Р. (1999), Обработка сигналов в дискретном времени (2-е изд.), Аппер-Сэддл-Ривер, Нью-Джерси: Прентис-Холл, ISBN 0-13-754920-2
- Палей, РЕАК ; Винер, Норберт (1934), Преобразования Фурье в сложной области , Публикации коллоквиума Американского математического общества, Провиденс, Род-Айленд: Американское математическое общество
- Пинский, Марк (2002), Введение в анализ Фурье и вейвлеты , Брукс/Коул, ISBN 978-0-534-37660-4
- Пуанкаре, Анри (1895), Аналитическая теория распространения тепла , Париж: Карре
- Полянин А.Д.; Манжиров А.В. (1998), Справочник по интегральным уравнениям , Бока-Ратон: CRC Press , ISBN 978-0-8493-2876-3
- Пресс, Уильям Х.; Фланнери, Брайан П.; Теукольский, Саул А.; Веттерлинг, Уильям Т. (1992), Численные рецепты на C: Искусство научных вычислений, второе издание (2-е изд.), Cambridge University Press
- Проакис, Джон Г.; Манолакис, Дмитрий Г. (1996). Цифровая обработка сигналов: принципы, алгоритмы и приложения (3-е изд.). Нью-Джерси: Прентис-Холл Интернэшнл. Бибкод : 1996dspp.book.....P . ISBN 9780133942897 . sAcfAQAAIAAJ.
- Рахман, Матюр (2011), Применение преобразований Фурье к обобщенным функциям , WIT Press, ISBN 978-1-84564-564-9
- Рудин, Уолтер (1987), Реальный и комплексный анализ (3-е изд.), Сингапур: McGraw Hill, ISBN 978-0-07-100276-9
- Симонен, П.; Олкконен, Х. (1985), «Быстрый метод вычисления интегрального преобразования Фурье посредством численного интегрирования Симпсона», Journal of Biomedical Engineering , 7 (4): 337–340, doi : 10.1016/0141-5425(85)90067-6 , PMID 4057997
- Смит, Джулиус О. «Математика дискретного преобразования Фурье (ДПФ) с аудиоприложениями — второе издание» . ccrma.stanford.edu . Проверено 29 декабря 2022 г.
Мы можем думать о настоящей синусоиде как о сумме комплексной синусоиды положительной частоты и отрицательной частоты.
- Штейн, Элиас; Шакарчи, Рами (2003), Анализ Фурье: введение , Princeton University Press , ISBN 978-0-691-11384-5
- Штейн, Элиас ; Вайс, Гвидо (1971), Введение в анализ Фурье в евклидовых пространствах , Принстон, Нью-Джерси: Princeton University Press , ISBN 978-0-691-08078-9
- Танеха, Х.К. (2008), «Глава 18: Интегралы Фурье и преобразования Фурье» , Advanced Engineering Mathematics , vol. 2, Нью-Дели, Индия: IK International Pvt Ltd, ISBN 978-8189866563
- Титчмарш, Э. (1986) [1948], Введение в теорию интегралов Фурье (2-е изд.), Оксфордский университет: Clarendon Press , ISBN 978-0-8284-0324-5
- Вретблад, Андерс (2000), Анализ Фурье и его приложения , Тексты для аспирантов по математике , том. 223, Нью-Йорк: Спрингер , ISBN. 978-0-387-00836-3
- Уиттакер, ET ; Уотсон, Дж.Н. (1927), Курс современного анализа (4-е изд.), Cambridge University Press
- Виддер, Дэвид Вернон; Винер, Норберт (август 1938 г.), «Замечания о классической формуле обращения для интеграла Лапласа» , Бюллетень Американского математического общества , 44 (8): 573–575, doi : 10.1090/s0002-9904-1938-06812-7
- Винер, Норберт (1949), Экстраполяция, интерполяция и сглаживание стационарных временных рядов с помощью инженерных приложений , Кембридж, Массачусетс: Technology Press, John Wiley & Sons и Chapman & Hall.
- Уилсон, Р.Г. (1995), Ряд Фурье и методы оптического преобразования в современной оптике , Нью-Йорк: Wiley , ISBN 978-0-471-30357-2
- Вольф, Курт Б. (1979), Интегральные преобразования в науке и технике , Springer , doi : 10.1007/978-1-4757-0872-1 , ISBN 978-1-4757-0874-5
- Йосида, К. (1968), Функциональный анализ , Springer , ISBN 978-3-540-58654-8
Внешние ссылки [ править ]
 СМИ, связанные с преобразованием Фурье, на Викискладе?
СМИ, связанные с преобразованием Фурье, на Викискладе? - Энциклопедия математики
- Вайсштейн, Эрик В. «Преобразование Фурье» . Математический мир .
- Преобразование Фурье в кристаллографии.

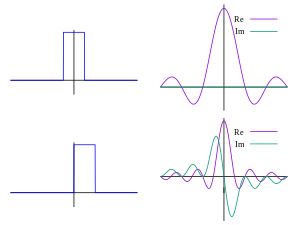







![{\displaystyle \textstyle x\in [-P/2,P/2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be4c2043b276e0f129991362775e5c5beff8982)



![{\displaystyle f(x)=\sum _{n=-\infty }^{\infty }c_{n}\,e^{i2\pi {\tfrac {n}{P}}x},\quad \textstyle x\in [-P/2,P/2].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/179ca2af800697798c172e1b58a650fbe2a1ccc6)














































































































































![{\displaystyle {\mathcal {F}}[\psi ]=\lambda \psi ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb312a1e0c7fe50ae6f17f3b157e13671bdd307e)

![{\displaystyle \left[U\left({\frac {1}{2\pi }}{\frac {d}{dx}}\right)+U(x)\right]\psi (x)=0 }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbdeac78597b20e0cc63dafce13269df2332ca31)






![{\displaystyle \left[W\left({\frac {i}{2\pi }}{\frac {d}{dx}}\right)+W(x)\right]\psi (x)=C \psi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d064e51b07fbf1e010b2aacf43bf894c516e0c92)



![{\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\ mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)



=\int dxf(x)\sum _{n\geq 0}(-i)^{n}\psi _{n}(x) \psi _{n}(\xi)~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eada95a2763cb70e97d43afd2f1f557fd2f046b)

![{\displaystyle {\mathcal {F}}[\psi ]=e^{-itN}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/271ffa7285358aed34c7ccbdadcc08d3da01dd90)
















































































![{\displaystyle {\begin{aligned}y(x,t)=\int _{0}^{\infty }d\xi {\Bigl [}&a_{+}(\xi)\cos {\bigl (} 2\pi \xi (x+t){\bigr )}+a_{-}(\xi )\cos {\bigl (}2\pi \xi (xt){\bigr )}+{}\\&b_ {+}(\xi )\sin {\bigl (}2\pi \xi (x+t){\bigr )}+b_{-}(\xi )\sin \left(2\pi \xi (xt )\right){\Bigr ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a65c9bf34f6bc5abac0d29243bda58f8c3310c2d)


















































































































































































































































![{\displaystyle \chi _{[0,1]}(|\mathbf {x} |)\left (1-|\mathbf {x} |^{2}\right)^{\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f3e6c1f52f0ee9366c40ee6f67c65f11dbd03a)




























