Вейвлет-преобразование

В математике вейвлет -ряд — это представление интегрируемой с квадратом ( действительной или комплекснозначной ) функции с помощью определенного ортонормированного ряда , генерируемого вейвлетом . В этой статье дается формальное математическое определение ортонормированного вейвлета и интегрального вейвлет-преобразования . ^[1]^[2]^[3]^[4]^[5]

Определение [ править ]

Функция $\psi \,\in \,L^{2}(\mathbb {R} )$ называется ортонормированным вейвлетом , если его можно использовать для определения гильбертового базиса , то есть полной ортонормированной системы , для гильбертова пространства. $L^{2}\left(\mathbb {R} \right)$ квадратично интегрируемых функций.

Базис Гильберта строится как семейство функций $\{\psi _{jk}:\,j,\,k\,\in \,\mathbb {Z} \}$ посредством диадических переводов и расширений $\psi \,$ ,

\psi _{jk}(x)=2^{\frac {j}{2}}\psi \left(2^{j}x-k\right)\,

для целых чисел $j,\,k\,\in \,\mathbb {Z}$ .

Если под стандартным внутренним продуктом на $L^{2}\left(\mathbb {R} \right)$ ,

\langle f,g\rangle =\int _{-\infty }^{\infty }f(x){\overline {g(x)}}dx

это семейство ортонормировано, это ортонормированная система:

{\begin{aligned}\langle \psi _{jk},\psi _{lm}\rangle &=\int _{-\infty }^{\infty }\psi _{jk}(x){\overline {\psi _{lm}(x)}}dx\\&=\delta _{jl}\delta _{km}\end{aligned}}

где $\delta _{jl}\,$ это дельта Кронекера .

Полнота удовлетворяется, если каждая функция $f\,\in \,L^{2}\left(\mathbb {R} \right)$ может быть расширен в базисе как

f(x)=\sum _{j,k=-\infty }^{\infty }c_{jk}\psi _{jk}(x)

при этом под сходимостью ряда понимается сходимость по норме . Такое представление f известно как вейвлет-серия . Это означает, что ортонормированный вейвлет самодуален .

Интегральное вейвлет-преобразование — это интегральное преобразование, определяемое как

\left[W_{\psi }f\right](a,b)={\frac {1}{\sqrt {|a|}}}\int _{-\infty }^{\infty }{\overline {\psi \left({\frac {x-b}{a}}\right)}}f(x)dx\,

Вейвлет -коэффициенты $c_{jk}$ затем даются

c_{jk}=\left[W_{\psi }f\right]\left(2^{-j},k2^{-j}\right)

Здесь, $a=2^{-j}$ называется бинарной дилатацией или диадической дилатацией , и $b=k2^{-j}$ это бинарная или диадическая позиция .

Принцип [ править ]

Фундаментальная идея вейвлет-преобразований заключается в том, что преобразование должно допускать только изменения во времени, но не в форме, что накладывает ограничение на выбор подходящих базисных функций. Ожидается, что изменения временного расширения будут соответствовать соответствующей частоте анализа базовой функции. На основе принципа неопределенности обработки сигналов,

\Delta t\Delta \omega \geq {\frac {1}{2}}

где $t$ представляет время и $\omega$ угловая частота ( $\omega =2\pi f$ , где $f$ обычная частота ).

Чем выше требуемое разрешение по времени, тем ниже должно быть разрешение по частоте. Чем большее расширение окон анализа выбрано, тем больше значение $\Delta t$ .

Когда $\Delta t$ большой,

Плохое разрешение времени
Хорошее частотное разрешение
Низкая частота, большой коэффициент масштабирования

Когда $\Delta t$ маленький

Хорошее временное разрешение
Плохое разрешение по частоте
Высокая частота, малый коэффициент масштабирования

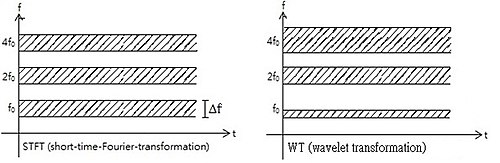
Другими словами, базисная функция $\psi$ можно рассматривать как импульсную характеристику системы, при которой функция $x(t)$ был отфильтрован. Преобразованный сигнал предоставляет информацию о времени и частоте. Таким образом, вейвлет-преобразование содержит информацию, аналогичную кратковременному преобразованию Фурье , но с дополнительными специальными свойствами вейвлетов, которые проявляются при разрешении во времени на более высоких частотах анализа базисной функции. Разница во временном разрешении на возрастающих частотах для преобразования Фурье и вейвлет-преобразования показана ниже. Однако обратите внимание, что разрешение по частоте уменьшается с увеличением частоты, в то время как временное разрешение увеличивается. Это следствие принципа неопределенности Фурье неверно отображено на рисунке.

Это показывает, что вейвлет-преобразование хорошо обеспечивает временное разрешение на высоких частотах, в то время как для медленно меняющихся функций частотное разрешение является замечательным.

Другой пример: анализ трех наложенных друг на друга синусоидальных сигналов. $y(t)\;=\;\sin(2\pi f_{0}t)\;+\;\sin(4\pi f_{0}t)\;+\;\sin(8\pi f_{0}t)$ с STFT и вейвлет-преобразованием.

Вейвлет-сжатие [ править ]

Вейвлет-сжатие — это форма сжатия данных, хорошо подходящая для сжатия изображений (иногда также сжатия видео и аудио ). Известные реализации — JPEG 2000 , DjVu и ECW для неподвижных изображений, JPEG XS , CineForm от BBC и Dirac . Цель состоит в том, чтобы хранить данные изображения в файле как можно меньше места . Вейвлет-сжатие может быть как без потерь , так и с потерями . ^[6]

Используя вейвлет-преобразование, методы вейвлет-сжатия подходят для представления переходных процессов , таких как перкуссионные звуки в аудио или высокочастотные компоненты в двумерных изображениях, например, изображения звезд на ночном небе. Это означает, что переходные элементы сигнала данных могут быть представлены меньшим объемом информации, чем было бы в случае, если бы какое-либо другое преобразование, например более распространенное дискретное косинусное преобразование использовалось .

Дискретное вейвлет-преобразование успешно применяется для сжатия сигналов электрокардиографа (ЭКГ). ^[7] В данной работе используется высокая корреляция между соответствующими вейвлет-коэффициентами сигналов последовательных сердечных циклов с использованием линейного прогнозирования.

Вейвлет-сжатие неэффективно для всех типов данных. Вейвлет-сжатие хорошо обрабатывает переходные сигналы. Но гладкие периодические сигналы лучше сжимаются с помощью других методов, в частности, традиционного гармонического анализа в частотной области с преобразованиями Фурье . Сжатие данных, имеющих как переходные, так и периодические характеристики, может быть выполнено с помощью гибридных методов, в которых используются вейвлеты наряду с традиционным гармоническим анализом. Например, Vorbis аудиокодек в основном использует модифицированное дискретное косинусное преобразование для сжатия звука (который обычно является плавным и периодическим), однако позволяет добавить банк гибридных вейвлет-фильтров для улучшения воспроизведения переходных процессов. ^[8]

См. «Дневник разработчика x264: Проблемы с вейвлетами» (2010 г.), где обсуждаются практические вопросы современных методов использования вейвлетов для сжатия видео.

Метод [ править ]

Сначала применяется вейвлет-преобразование. В результате получается столько коэффициентов , сколько пикселей в изображении (т. е. сжатие еще не производится, поскольку это всего лишь преобразование). Эти коэффициенты затем можно будет легче сжать, поскольку информация статистически сконцентрирована всего в нескольких коэффициентах. Этот принцип называется кодированием с преобразованием . После этого коэффициенты квантуются , а квантованные значения подвергаются энтропийному кодированию и/или кодированию длины серии .

В некоторых одномерных и двумерных приложениях вейвлет-сжатия используется метод, называемый «вейвлет-следы». ^[9]^[10]

Оценка [ править ]

Требование к сжатию изображений [ править ]

Для большинства естественных изображений спектральная плотность нижних частот выше. ^[11]В результате информация низкочастотного сигнала (опорного сигнала) обычно сохраняется, тогда как информация подробного сигнала отбрасывается. С точки зрения сжатия и реконструкции изображений вейвлет при выполнении сжатия изображений должен соответствовать следующим критериям:

Возможность преобразовать более оригинальное изображение в опорный сигнал.
Реконструкция с высочайшей точностью на основе опорного сигнала.
Не должно приводить к появлению артефактов в изображении, восстановленном только по опорному сигналу.

Требование к отклонению смены и поведению звонка [ править ]

Система сжатия вейвлет-изображений включает в себя фильтры и прореживание, поэтому ее можно описать как систему с линейным сдвигом. Типичная диаграмма вейвлет-преобразования показана ниже:

Система преобразования содержит два фильтра анализа (фильтр нижних частот $h_{0}(n)$ и фильтр верхних частот $h_{1}(n)$ ), процесс прореживания, процесс интерполяции и два фильтра синтеза ( $g_{0}(n)$ и $g_{1}(n)$ ). Система сжатия и реконструкции обычно включает в себя низкочастотные компоненты, которыми являются фильтры анализа. $h_{0}(n)$ для сжатия изображений и фильтров синтеза $g_{0}(n)$ для реконструкции. Чтобы оценить такую систему, мы можем ввести импульс $\delta (n-n_{i})$ и наблюдать за его реконструкцией $h(n-n_{i})$ ; Оптимальным вейвлетом являются те, которые обеспечивают минимальную дисперсию сдвига и боковые лепестки. $h(n-n_{i})$ . Несмотря на то, что вейвлет со строгим отклонением сдвига нереалистичен, можно выбрать вейвлет с лишь небольшим отклонением сдвига. Например, мы можем сравнить дисперсию сдвига двух фильтров: ^[12]

Биортогональные фильтры для вейвлет-сжатия изображений
		Длина	Коэффициенты фильтра	Регулярность
Вейвлет-фильтр 1	Н0	9	.852699, .377402, -.110624, -.023849, .037828	1.068
Вейвлет-фильтр 1	G0	7	.788486, .418092, -.040689, -.064539	1.701
Вейвлет-фильтр 2	Н0	6	.788486, .047699, -.129078	0.701
Вейвлет-фильтр 2	G0	10	.615051, .133389, -.067237, .006989, .018914	2.068

Наблюдая за импульсными характеристиками двух фильтров, мы можем сделать вывод, что второй фильтр менее чувствителен к местоположению входа (т.е. это вариант с меньшим сдвигом).

Еще одной важной проблемой сжатия и реконструкции изображений является колебательное поведение системы, которое может привести к серьезным нежелательным артефактам в реконструированном изображении. Чтобы добиться этого, вейвлет-фильтры должны иметь большое отношение пика к боковым лепесткам.

До сих пор мы обсуждали одномерную трансформацию системы сжатия изображений. Эту проблему можно распространить на два измерения, при этом предлагается более общий термин — смещаемые многомасштабные преобразования. ^[13]

Вывод характеристики импульсной

Как упоминалось ранее, импульсный отклик можно использовать для оценки системы сжатия/восстановления изображения.

Для входной последовательности $x(n)=\delta (n-n_{i})$ , опорный сигнал $r_{1}(n)$ после одного уровня разложения $x(n)*h_{0}(n)$ подвергается децимации в два раза, в то время как $h_{0}(n)$ представляет собой фильтр нижних частот. Аналогично, следующий опорный сигнал $r_{2}(n)$ получается путем $r_{1}(n)*h_{0}(n)$ проходит децимацию в два раза. После L уровней разложения (и децимации) ответ анализа получается путем сохранения одного из каждых $2^{L}$ образцы: $h_{A}^{(L)}(n,n_{i})=f_{h0}^{(L)}(n-n_{i}/2^{L})$ .

С другой стороны, чтобы восстановить сигнал x(n), мы можем рассмотреть опорный сигнал $r_{L}(n)=\delta (n-n_{j})$ . Если деталь сигнализирует $d_{i}(n)$ равны нулю для $1\leq i\leq L$ , то опорный сигнал на предыдущем этапе ( $L-1$ этап) есть $r_{L-1}(n)=g_{0}(n-2n_{j})$ , который получается интерполяцией $r_{L}(n)$ и свертки с $g_{0}(n)$ . Аналогично процедура повторяется для получения опорного сигнала. $r(n)$ на этапе $L-2,L-3,....,1$ . После L итераций вычисляется импульсная характеристика синтеза: $h_{s}^{(L)}(n,n_{i})=f_{g0}^{(L)}(n/2^{L}-n_{j})$ , который связывает опорный сигнал $r_{L}(n)$ и восстановленный сигнал.

Чтобы получить общую систему анализа/синтеза уровня L, ответы анализа и синтеза объединяются, как показано ниже:

$h_{AS}^{(L)}(n,n_{i})=\sum _{k}f_{h0}^{(L)}(k-n_{i}/2^{L})f_{g0}^{(L)}(n/2^{L}-k)$ .

Наконец, отношение пика к первому боковому лепестку и среднее значение второго бокового лепестка общей импульсной характеристики. $h_{AS}^{(L)}(n,n_{i})$ может использоваться для оценки эффективности сжатия вейвлет-изображения.

с преобразованием Фурье и частотно- анализом Сравнение временным

Трансформировать	Представление	Вход
преобразование Фурье	${\hat {X}}(f)=\int _{-\infty }^{\infty }x(t)e^{-i2\pi ft}\,dt$	$f$ : частота
Частотно-временной анализ	$X(t,f)$	$t$ время; $f$ частота
Вейвлет-преобразование	$X(a,b)={\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }{\overline {\Psi \left({\frac {t-b}{a}}\right)}}x(t)\,dt$	$a$ масштабирование; $b$ коэффициент временного сдвига

Вейвлеты имеют некоторые небольшие преимущества перед преобразованиями Фурье в сокращении вычислений при исследовании определенных частот. Однако они редко бывают более чувствительными, и действительно, обычный вейвлет Морле математически идентичен кратковременному преобразованию Фурье с использованием оконной функции Гаусса. ^[14]Исключение составляет поиск сигналов известной, несинусоидальной формы (например, сердцебиения); в этом случае использование согласованных вейвлетов может превзойти стандартный анализ STFT/Morlet. ^[15]

практические Другие применения

Вейвлет-преобразование может предоставить нам частоту сигналов и время, связанное с этими частотами, что делает его очень удобным для применения во многих областях. Например, обработка сигналов ускорений для анализа походки, ^[16] для обнаружения неисправностей, ^[17] для разработки кардиостимуляторов малой мощности, а также для сверхширокополосной (СШП) беспроводной связи. ^[18]^[19]^[20]

Дискретизация $c-\tau$ ось
Применили следующую дискретизацию частоты и времени:

${\begin{aligned}c_{n}&=c_{0}^{n}\\\tau _{m}&=m\cdot T\cdot c_{0}^{n}\end{aligned}}$

Что приводит к вейвлетам вида, дискретная формула для базового вейвлета:

$\Psi (k,n,m)={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \Psi \left[{\frac {k-mc_{0}^{n}}{c_{0}^{n}}}T\right]={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \Psi \left[\left({\frac {k}{c_{0}^{n}}}-m\right)T\right]$

Такие дискретные вейвлеты можно использовать для преобразования:

$Y_{DW}(n,m)={\frac {1}{\sqrt {c_{0}^{n}}}}\cdot \sum _{k=0}^{K-1}y(k)\cdot \Psi \left[\left({\frac {k}{c_{0}^{n}}}-m\right)T\right]$
Реализация через БПФ (быстрое преобразование Фурье)
Как видно из представления вейвлет-преобразования (показано ниже)

$Y_{W}(c,\tau )={\frac {1}{\sqrt {c}}}\cdot \int _{-\infty }^{\infty }y(t)\cdot \Psi \left({\frac {t-\tau }{c}}\right)\,dt$

где $c$ масштабный коэффициент, $\tau$ представляет собой коэффициент временного сдвига
и, как уже упоминалось в этом контексте, вейвлет-преобразование соответствует свертке функции $y(t)$ и вейвлет-функция. Свертку можно реализовать как умножение в частотной области. При этом следующий подход к реализации приводит к:
- Фурье-преобразование сигнала $y(k)$ с БПФ
- Выбор дискретного масштабного коэффициента $c_{n}$
- Масштабирование вейвлет-базиса по этому коэффициенту $c_{n}$ и последующее БПФ этой функции
- Умножение на преобразованный сигнал YFFT первого шага
- Обратное преобразование произведения во временную область приводит к $Y_{W}(c,\tau )$ для различных дискретных значений $\tau$ и дискретное значение $c_{n}$
- Вернемся ко второму шагу, пока все дискретные значения масштабирования для $c_{n}$ обрабатываются
Существует множество различных типов вейвлет-преобразований для конкретных целей. См. также полный список преобразований, связанных с вейвлетами , но наиболее распространенные перечислены ниже: вейвлет «Мексиканская шляпа» , вейвлет Хаара , вейвлет Добеши , треугольный вейвлет.
Обнаружение неисправностей в электроэнергетических системах. ^[21]
Локально адаптивная статистическая оценка функций, гладкость которых существенно варьируется в пределах области, или, более конкретно, оценка функций, которые разрежены в области вейвлетов. ^[22]

- вейвлеты Временно причинные

Для обработки временных сигналов в реальном времени важно, чтобы вейвлет-фильтры не обращались к значениям сигналов из будущего, а также чтобы можно было получить минимальные временные задержки. Представления вейвлетов, причинных временем, были разработаны Szu et al. ^[23] и Линдеберг, ^[24] причем последний метод также включает в себя рекурсивную по времени реализацию, эффективно использующую память.

Синхронно-сжатое преобразование [ править ]

Синхронно-сжатое преобразование может значительно улучшить временное и частотное разрешение частотно-временного представления, полученного с использованием обычного вейвлет-преобразования. ^[25]^[26]

См. также [ править ]

Биномиальный QMF (также известный как вейвлет Добеши )
Биортогональный почти койфлетный базис , который показывает, что вейвлет для сжатия изображений также может быть почти койфлетным (почти ортогональным)
Преобразование чирплета
Комплексное вейвлет-преобразование
Преобразование с постоянной Q
Непрерывное вейвлет-преобразование
Вейвлет Добеши
Дискретное вейвлет-преобразование
Формат DjVu использует для сжатия изображений алгоритм IW44 на основе вейвлетов.
Двойной вейвлет
ECW изображений на основе вейвлетов, — формат геопространственных разработанный для скорости и эффективности обработки.
Вейвлет Габора
Вейвлет для волос
JPEG 2000 на основе вейвлетов. сжатия изображений — стандарт
Спектральный анализ методом наименьших квадратов
Вейвлет Морле
Мультиразрешительный анализ
MrSID , формат изображения, разработанный на основе оригинальных исследований вейвлет-сжатия в Национальной лаборатории Лос-Аламоса (LANL).
S-преобразование
Скалеограммы — тип спектрограммы , генерируемой с использованием вейвлетов вместо кратковременного преобразования Фурье.
Установить разделение в иерархических деревьях
Кратковременное преобразование Фурье
Стационарное вейвлет-преобразование
Частотно-временное представление
Вейвлет

Ссылки [ править ]

^ Мейер, Ив (1992), Вейвлеты и операторы, Кембридж, Великобритания: Издательство Кембриджского университета, ISBN 0-521-42000-8
^ Чуи, Чарльз К. (1992), Введение в вейвлеты, Сан-Диего, Калифорния: Academic Press, ISBN 0-12-174584-8
^ Добеши, Ингрид. (1992), Десять лекций по вейвлетам, SIAM, ISBN 978-0-89871-274-2
^ Акансу, Али Н.; Хаддад, Ричард А. (1992), Разложение сигнала с несколькими разрешениями: преобразования, поддиапазоны и вейвлеты, Бостон, Массачусетс: Academic Press, ISBN 978-0-12-047141-6
^ Гадерпур, Э.; Пагиатакис, С.Д.; Хасан, Квебек (2021). «Опрос по обнаружению изменений и анализу временных рядов с помощью приложений» . Прикладные науки . 11 (13): 6141. дои : 10.3390/app11136141 . hdl : 11573/1655273 .
^ JPEG 2000 , например, может использовать вейвлет 5/3 для преобразования без потерь (обратимого) и вейвлет 9/7 для преобразования с потерями (необратимого).
^ Рамакришнан, АГ; Саха, С. (1997). «Кодирование ЭКГ с помощью линейного прогнозирования на основе вейвлетов» (PDF) . Транзакции IEEE по биомедицинской инженерии . 44 (12): 1253–1261. дои : 10.1109/10.649997 . ПМИД 9401225 . S2CID 8834327 .
^ «Спецификация Vorbis I» . Фонд Xiph.Org . 04.07.2020. Архивировано из оригинала 3 апреля 2022 г. Проверено 10 апреля 2022 г. Vorbis I — это кодек монолитного преобразования с прямой адаптацией, основанный на модифицированном дискретном косинусном преобразовании. Кодек структурирован так, чтобы обеспечить добавление гибридного банка вейвлет-фильтров в Vorbis II, чтобы обеспечить лучший переходный отклик и воспроизведение с использованием преобразования, лучше подходящего для локализованных временных событий.
^ Н. Малмуруган, А. Шанмугам, С. Джаяраман и В.В. Динеш Чандер. «Новый алгоритм сжатия изображений с использованием вейвлет-следов»
^ Хо Татт Вэй и Джеоти, В. «Схема сжатия сигналов ЭКГ на основе вейвлет-следов». Хо Татт Вэй; Джеоти, В. (2004). «Схема сжатия сигналов ЭКГ на основе вейвлет-следов». 2004 г. Конференция IEEE Region 10 TENCON 2004 г. Том. А. п. 283. дои : 10.1109/TENCON.2004.1414412 . ISBN 0-7803-8560-8 . S2CID 43806122 .
^ Дж. Филд, Дэвид (1987). «Связь между статистикой естественных изображений и ответными свойствами клеток коры» (PDF) . J. Опт. Соц. Являюсь. А. 4 (12): 2379–2394. Бибкод : 1987JOSAA...4.2379F . дои : 10.1364/JOSAA.4.002379 . ПМИД 3430225 .
^ Вилласенор, Джон Д. (август 1995 г.). «Оценка вейвлет-фильтра для сжатия изображения». Транзакции IEEE при обработке изображений . 4 (8): 1053–60. Бибкод : 1995ITIP....4.1053V . дои : 10.1109/83.403412 . ПМИД 18291999 .
^ Симончелли, EP; Фриман, WT; Адельсон, Э.Х.; Хигер, диджей (1992). «Сдвигаемые многомасштабные преобразования». Транзакции IEEE по теории информации . 38 (2): 587–607. дои : 10.1109/18.119725 . S2CID 43701174 .
^ Брунс, Андреас (2004). «Анализ сигналов на основе Фурье, Гильберта и вейвлетов: действительно ли это разные подходы?». Журнал методов нейробиологии . 137 (2): 321–332. doi : 10.1016/j.jneumeth.2004.03.002 . ПМИД 15262077 . S2CID 21880274 .
^ Кранц, Стивен Г. (1999). Панорама гармонического анализа . Математическая ассоциация Америки. ISBN 0-88385-031-1 .
^ Мартин, Э. (2011). «Новый метод оценки длины шага с помощью акселерометров сети области тела». Тематическая конференция IEEE 2011 г. по биомедицинским беспроводным технологиям, сетям и сенсорным системам . стр. 79–82. doi : 10.1109/BIOWIRELESS.2011.5724356 . ISBN 978-1-4244-8316-7 . S2CID 37689047 .
^ Лю, Цзе (2012). «Вейвлет-спектральный анализ Шеннона усеченных сигналов вибрации для обнаружения зарождающихся неисправностей оборудования». Измерительная наука и технология . 23 (5): 1–11. Бибкод : 2012MeScT..23e5604L . дои : 10.1088/0957-0233/23/5/055604 . S2CID 121684952 .
^ Акансу, АН; Сердейн, Вашингтон; Селесник, И.В. (2010). «Новые приложения вейвлетов: обзор» (PDF) . Физическое общение . 3 : 1–18. дои : 10.1016/j.phycom.2009.07.001 .
^ Шейбани, Э.; Джавиди, Г. (декабрь 2009 г.). «Уменьшение размерности и удаление шума в наборах данных беспроводной сенсорной сети». 2009 Вторая международная конференция по компьютерной и электротехнике . Том. 2. стр. 674–677. дои : 10.1109/ICCEE.2009.282 . ISBN 978-1-4244-5365-8 . S2CID 17066179 .
^ Шейбани, Э.О.; Джавиди, Г. (май 2012 г.). «Банки фильтров с разным разрешением для улучшения изображений SAR». Международная конференция по системам и информатике 2012 (ICSAI2012) . стр. 2702–2706. дои : 10.1109/ICSAI.2012.6223611 . ISBN 978-1-4673-0199-2 . S2CID 16302915 .
^ Сильва, К.М.; Соуза, бакалавр; Брито, НРД (октябрь 2006 г.). «Обнаружение и классификация неисправностей в линиях электропередачи на основе вейвлет-преобразования и ИНС». Транзакции IEEE при доставке электроэнергии . 21 (4): 2058–2063. дои : 10.1109/TPWRD.2006.876659 . S2CID 36881450 .
^ Вассерман, Луизиана (2005). Вся непараметрическая статистика .
^ Сзу, Гарольд Х.; Телфер, Брайан А.; Ломанн, Адольф В. (1992). «Каузальное аналитическое вейвлет-преобразование». Оптическая инженерия . 31 (9): 1825. Бибкод : 1992OptEn..31.1825S . дои : 10.1117/12.59911 .
^ Линдеберг, Т. (23 января 2023 г.). «Причинно-временное и рекурсивное по времени масштабно-пространственное представление временных сигналов и прошлого времени» . Биологическая кибернетика . 117 (1–2): 21–59. дои : 10.1007/s00422-022-00953-6 . ПМЦ 10160219 . ПМИД 36689001 .
^ Добеши, Ингрид; Лу, Цзяньфэн; Ву, Хау-Тьенг (12 декабря 2009 г.). «Синхросжатые вейвлет-преобразования: инструмент для декомпозиции эмпирических мод». arXiv : 0912.2437 [ math.NA ].
^ Цюй, Хунья; Ли, Тяньтянь; Чен, Генда (01 января 2019 г.). «Синхронно-сжатое адаптивное вейвлет-преобразование с оптимальными параметрами для произвольных временных рядов» . Механические системы и обработка сигналов . 114 : 366–377. Бибкод : 2019MSSP..114..366Q . дои : 10.1016/j.ymssp.2018.05.020 . S2CID 126007150 .

^[1]

Внешние ссылки [ править ]

Амара Грапс (июнь 1995 г.). «Введение в вейвлеты» . IEEE Вычислительная наука и инженерия . 2 (2): 50–61. дои : 10.1109/99.388960 .
Роби Поликар (12 января 2001 г.). «Урок по вейвлетам» .
Краткое введение в вейвлеты Рене Пушингера

^ Прасад, Ахилеш; Маан, Джитендрасингх; Верма, Сандип Кумар (2021). «Вейвлет-преобразования, связанные с индексным преобразованием Уиттекера» . Математические методы в прикладных науках . 44 (13): 10734–10752. Бибкод : 2021MMAS...4410734P . дои : 10.1002/ммма.7440 . ISSN 1099-1476 . S2CID 235556542 .

[1] Мейер, Ив (1992), Вейвлеты и операторы, Кембридж, Великобритания: Издательство Кембриджского университета, ISBN 0-521-42000-8

[2] Чуи, Чарльз К. (1992), Введение в вейвлеты, Сан-Диего, Калифорния: Academic Press, ISBN 0-12-174584-8

[3] Добеши, Ингрид. (1992), Десять лекций по вейвлетам, SIAM, ISBN 978-0-89871-274-2

[4] Акансу, Али Н.; Хаддад, Ричард А. (1992), Разложение сигнала с несколькими разрешениями: преобразования, поддиапазоны и вейвлеты, Бостон, Массачусетс: Academic Press, ISBN 978-0-12-047141-6

[5] Гадерпур, Э.; Пагиатакис, С.Д.; Хасан, Квебек (2021). «Опрос по обнаружению изменений и анализу временных рядов с помощью приложений» . Прикладные науки . 11 (13): 6141. дои : 10.3390/app11136141 . hdl : 11573/1655273 .

[6] JPEG 2000 , например, может использовать вейвлет 5/3 для преобразования без потерь (обратимого) и вейвлет 9/7 для преобразования с потерями (необратимого).

[7] Рамакришнан, АГ; Саха, С. (1997). «Кодирование ЭКГ с помощью линейного прогнозирования на основе вейвлетов» (PDF) . Транзакции IEEE по биомедицинской инженерии . 44 (12): 1253–1261. дои : 10.1109/10.649997 . ПМИД 9401225 . S2CID 8834327 .

[8] «Спецификация Vorbis I» . Фонд Xiph.Org . 04.07.2020. Архивировано из оригинала 3 апреля 2022 г. Проверено 10 апреля 2022 г. Vorbis I — это кодек монолитного преобразования с прямой адаптацией, основанный на модифицированном дискретном косинусном преобразовании. Кодек структурирован так, чтобы обеспечить добавление гибридного банка вейвлет-фильтров в Vorbis II, чтобы обеспечить лучший переходный отклик и воспроизведение с использованием преобразования, лучше подходящего для локализованных временных событий.

[9] Н. Малмуруган, А. Шанмугам, С. Джаяраман и В.В. Динеш Чандер. «Новый алгоритм сжатия изображений с использованием вейвлет-следов»

[10] Хо Татт Вэй и Джеоти, В. «Схема сжатия сигналов ЭКГ на основе вейвлет-следов». Хо Татт Вэй; Джеоти, В. (2004). «Схема сжатия сигналов ЭКГ на основе вейвлет-следов». 2004 г. Конференция IEEE Region 10 TENCON 2004 г. Том. А. п. 283. дои : 10.1109/TENCON.2004.1414412 . ISBN 0-7803-8560-8 . S2CID 43806122 .

[11] Дж. Филд, Дэвид (1987). «Связь между статистикой естественных изображений и ответными свойствами клеток коры» (PDF) . J. Опт. Соц. Являюсь. А. 4 (12): 2379–2394. Бибкод : 1987JOSAA...4.2379F . дои : 10.1364/JOSAA.4.002379 . ПМИД 3430225 .

[12] Вилласенор, Джон Д. (август 1995 г.). «Оценка вейвлет-фильтра для сжатия изображения». Транзакции IEEE при обработке изображений . 4 (8): 1053–60. Бибкод : 1995ITIP....4.1053V . дои : 10.1109/83.403412 . ПМИД 18291999 .

[13] Симончелли, EP; Фриман, WT; Адельсон, Э.Х.; Хигер, диджей (1992). «Сдвигаемые многомасштабные преобразования». Транзакции IEEE по теории информации . 38 (2): 587–607. дои : 10.1109/18.119725 . S2CID 43701174 .

[14] Брунс, Андреас (2004). «Анализ сигналов на основе Фурье, Гильберта и вейвлетов: действительно ли это разные подходы?». Журнал методов нейробиологии . 137 (2): 321–332. doi : 10.1016/j.jneumeth.2004.03.002 . ПМИД 15262077 . S2CID 21880274 .

[15] Кранц, Стивен Г. (1999). Панорама гармонического анализа . Математическая ассоциация Америки. ISBN 0-88385-031-1 .

[16] Мартин, Э. (2011). «Новый метод оценки длины шага с помощью акселерометров сети области тела». Тематическая конференция IEEE 2011 г. по биомедицинским беспроводным технологиям, сетям и сенсорным системам . стр. 79–82. doi : 10.1109/BIOWIRELESS.2011.5724356 . ISBN 978-1-4244-8316-7 . S2CID 37689047 .

[17] Лю, Цзе (2012). «Вейвлет-спектральный анализ Шеннона усеченных сигналов вибрации для обнаружения зарождающихся неисправностей оборудования». Измерительная наука и технология . 23 (5): 1–11. Бибкод : 2012MeScT..23e5604L . дои : 10.1088/0957-0233/23/5/055604 . S2CID 121684952 .

[18] Акансу, АН; Сердейн, Вашингтон; Селесник, И.В. (2010). «Новые приложения вейвлетов: обзор» (PDF) . Физическое общение . 3 : 1–18. дои : 10.1016/j.phycom.2009.07.001 .

[19] Шейбани, Э.; Джавиди, Г. (декабрь 2009 г.). «Уменьшение размерности и удаление шума в наборах данных беспроводной сенсорной сети». 2009 Вторая международная конференция по компьютерной и электротехнике . Том. 2. стр. 674–677. дои : 10.1109/ICCEE.2009.282 . ISBN 978-1-4244-5365-8 . S2CID 17066179 .

[20] Шейбани, Э.О.; Джавиди, Г. (май 2012 г.). «Банки фильтров с разным разрешением для улучшения изображений SAR». Международная конференция по системам и информатике 2012 (ICSAI2012) . стр. 2702–2706. дои : 10.1109/ICSAI.2012.6223611 . ISBN 978-1-4673-0199-2 . S2CID 16302915 .

[21] Сильва, К.М.; Соуза, бакалавр; Брито, НРД (октябрь 2006 г.). «Обнаружение и классификация неисправностей в линиях электропередачи на основе вейвлет-преобразования и ИНС». Транзакции IEEE при доставке электроэнергии . 21 (4): 2058–2063. дои : 10.1109/TPWRD.2006.876659 . S2CID 36881450 .

[22] Вассерман, Луизиана (2005). Вся непараметрическая статистика .

[23] Сзу, Гарольд Х.; Телфер, Брайан А.; Ломанн, Адольф В. (1992). «Каузальное аналитическое вейвлет-преобразование». Оптическая инженерия . 31 (9): 1825. Бибкод : 1992OptEn..31.1825S . дои : 10.1117/12.59911 .

[24] Линдеберг, Т. (23 января 2023 г.). «Причинно-временное и рекурсивное по времени масштабно-пространственное представление временных сигналов и прошлого времени» . Биологическая кибернетика . 117 (1–2): 21–59. дои : 10.1007/s00422-022-00953-6 . ПМЦ 10160219 . ПМИД 36689001 .

[25] Добеши, Ингрид; Лу, Цзяньфэн; Ву, Хау-Тьенг (12 декабря 2009 г.). «Синхросжатые вейвлет-преобразования: инструмент для декомпозиции эмпирических мод». arXiv : 0912.2437 [ math.NA ].

[26] Цюй, Хунья; Ли, Тяньтянь; Чен, Генда (01 января 2019 г.). «Синхронно-сжатое адаптивное вейвлет-преобразование с оптимальными параметрами для произвольных временных рядов» . Механические системы и обработка сигналов . 114 : 366–377. Бибкод : 2019MSSP..114..366Q . дои : 10.1016/j.ymssp.2018.05.020 . S2CID 126007150 .

[27] Прасад, Ахилеш; Маан, Джитендрасингх; Верма, Сандип Кумар (2021). «Вейвлет-преобразования, связанные с индексным преобразованием Уиттекера» . Математические методы в прикладных науках . 44 (13): 10734–10752. Бибкод : 2021MMAS...4410734P . дои : 10.1002/ммма.7440 . ISSN 1099-1476 . S2CID 235556542 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[1]