Стационарное вейвлет-преобразование

Стационарное вейвлет-преобразование ( SWT ) — это алгоритм вейвлет-преобразования , предназначенный для преодоления отсутствия трансляционной инвариантности дискретного вейвлет-преобразования (DWT). Трансляционная инвариантность достигается за счет удаления понижающих и повышающих дискретизаторов в DWT и повышения дискретизации коэффициентов фильтра в раз. $2^{(j-1)}$ в $j$уровень алгоритма. SWT является по своей сути избыточной схемой, поскольку выходные данные каждого уровня SWT содержат то же количество выборок, что и входные, поэтому для разложения N уровней существует избыточность N в вейвлет-коэффициентах. Этот алгоритм более известен как « алгоритм à trous » на французском языке (слово trous на английском означает «дырки»), что означает вставку нулей в фильтры. Он был введен Хольшнейдером и др.

Определение

Базовый алгоритм дискретного вейвлет-преобразования (DWT) адаптирован для получения стационарного вейвлет-преобразования (SWT), которое не зависит от источника. Подход SWT прост: к данным на каждом уровне применяются подходящие фильтры верхних и нижних частот , что приводит к созданию двух последовательностей на последующем уровне. Без использования методов понижающей дискретизации длина новых последовательностей сохраняется такой же, как и исходные последовательности. Вместо того, чтобы использовать прореживание, аналогичное стандартному вейвлет-преобразованию, которое удаляет элементы, фильтры на каждом уровне корректируются путем дополнения их нулями, как описано ниже:

${Zx}_{2j}=x_{j},\ {Zx}_{2j+1}=0\ for\ all\ integers\ j$

$D_{0}^{r}H^{\left[r\right]}=HD_{0}^{r}$

$D_{0}^{r}G^{\left[r\right]}=GD_{0}^{r}$

где $Z$ это оператор, который перемежает заданную последовательность нулями для всех целых чисел $j$.

$D_{0}^{r}$ это оператор двоичного прореживания

$H^{\left[r\right]}$ это фильтр с весами ${h_{2^{r}}^{\left[r\right]}}_{j}=h_{j}\ and\ h_{k}^{\left[r\right]}=0\ if\ k\ is\ not\ a\ multiple\ of\ 2^{r}.$

$G^{\left[r\right]}$ это фильтр с весами ${g_{2^{r}}^{\left[r\right]}}_{j}=h_{j}\ and\ g_{k}^{\left[r\right]}=0\ if\ k\ is\ not\ a\ multiple\ of\ 2^{r}.$

Конструкция фильтров $H^{\left[r\right]}$ и $G^{\left[r\right]}$ включает вставку нуля между каждой соседней парой элементов в фильтре $H^{\left[r-1\right]}$ и $G^{\left[r-1\right]}$ соответственно.

Обозначение $a^{J}$ как исходная последовательность $c^{J}$ требуется перед определением стационарного вейвлет-преобразования.

$a^{j-1}=H^{\left[J-j\right]}a^{j},\ for\ j=J,J-1,\ \ldots \ ,1\$

$b^{j-1}=G^{\left[J-j\right]}a^{j},for\ j=J,J-1,\ \ldots \ ,1$

где $a^{j}=b^{j},\ if\ length\ of\ a^{j}=2^{J}$

Выполнение

Следующая блок-схема изображает цифровую реализацию SWT.

Трехуровневый блок фильтров SWT.

На приведенной выше диаграмме фильтры на каждом уровне представляют собой версии предыдущего с повышенной дискретизацией (см. рисунок ниже).

SWT-фильтры

Приложения

Ниже приведены несколько применений SWT.

Улучшение изображения

SWT можно использовать для повышения разрешения изображения, чтобы обеспечить лучшее качество изображения. Основным недостатком повышения разрешения изображения с помощью обычного метода интерполяции является потеря высокочастотных составляющих. В результате происходит сглаживание интерполяции, обеспечивающее размытость изображения с отсутствием или уменьшенным присутствием мелких деталей, резких краев. Информация о высокочастотных компонентах (краях) имеет решающее значение для достижения лучшего качества изображения со сверхразрешением.

Сначала он разлагает входное изображение на различные изображения поддиапазонов, применяя одноуровневый DWT. Есть три изображения поддиапазонов для захвата высокочастотных компонентов входного изображения. После этого реализуется SWT, его цель состоит в том, чтобы уменьшить потери информации, вызванные понижающей дискретизацией в каждом поддиапазоне DWT. Усиленные и скорректированные высокочастотные поддиапазоны формируются путем суммирования высокочастотных поддиапазонов от DWT и SWT, в результате чего выходное изображение получается с заостренными краями.

Шумоподавление сигнала

Традиционная процедура шумоподавления в основном состоит из первого преобразования сигнала в другую область, затем применения пороговой обработки и, наконец, обратного преобразования для восстановления исходного сигнала. Стационарное вейвлет-преобразование введено для устранения явления Гиббса , вызванного процессом сдвига в дискретном вейвлет-преобразовании . Это явление влияет на качество изображения (шумы) после процесса реконструкции. Модифицированная процедура проста: сначала выполняется стационарное вейвлет-преобразование сигнала, определение порога и, наконец, обратное преобразование. Краткое объяснение выглядит следующим образом:

В отличие от дискретного вейвлет-преобразования, SWT не понижает дискретизацию сигнала на каждом уровне. Вместо этого он сохраняет исходную частоту дискретизации на протяжении всего процесса разложения, и это обеспечивает эффективную инкапсуляцию высоко- и низкочастотных компонентов. Поскольку шум часто распространяется по всем масштабам с небольшим вкладом по величине, пороговая обработка реализуется как следующий шаг к вейвлет-коэффициентам. Коэффициенты ниже определенного порогового уровня обнуляются или уменьшаются, что приводит к отделению сигнала от шума. После удаления или подавления шумовых коэффициентов, которые не учитываются в ходе реконструкции, очищенный от шума сигнал становится более четким.

Шумоподавление сигнала также широко используется при шумоподавлении биомедицинских сигналов (ЭКГ). шумоподавление изображения. Эффективность SWT в шумоподавлении сигнала делает его ценным инструментом в реальных приложениях в различных областях.

• Распознавание образов
• Классификация изображений мозга
• Патологическое обнаружение мозга

Пример кода

Вот пример применения стационарного вейвлет-преобразования к ЛМ-сигналу, закодированному с помощью Python3:

1. Установите необходимые пакеты в Python

   pip install numpy
   
   pip install matplotlib
   
   pip install pywt
   

2. Импортировать библиотеки в Python

   import numpy as np
   import matplotlib.pyplot as plt
   import pywt
   

3. Основной код

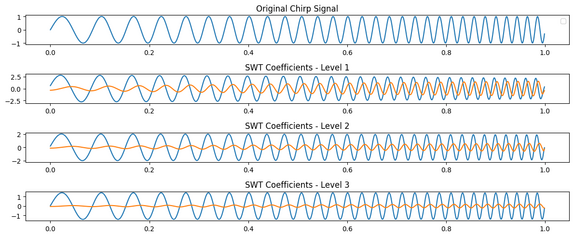
   # Generating a chirp signal
   t = np.linspace(0, 1, 1000, endpoint=False)
   frequency = 10 + 20 * t
   chirp_signal = np.sin(2 * np.pi * frequency * t)
   
   # Perform Stationary Wavelet Transform (SWT)
   wavelet = 'db1' # Daubechies wavelet
   level = 3 # Decomposition level
   coeffs = pywt.swt(chirp_signal, wavelet, level) # Coefficients
   
   # Plot the original chirp signal
   plt.figure(figsize=(12, 6))
   plt.subplot(level + 2, 1, 1)
   plt.plot(t, chirp_signal)
   plt.title('Original Chirp Signal')
   plt.legend()
   
   # Plot the SWT Coefficients
   for i in range(level):
       plt.subplot(level + 2, 1, i + 2)
       plt.plot(t, coeffs[i][0])
       plt.plot(t, coeffs[i][1])
       plt.title(f'SWT Coefficients - Level {i}')
   plt.tight_layout()
   plt.show()
   

4. Выход

   

Синонимы

• Избыточное вейвлет-преобразование
• Алгоритм отверстия
• Квазинепрерывное вейвлет-преобразование
• Вейвлет-преобразование, инвариантное к трансляции
• Вейвлет-преобразование, инвариантное к сдвигу
• Велоотжим
• Вейвлет-преобразование с максимальным перекрытием (MODWT)
• Непрореженное вейвлет-преобразование (UWT)

См. также

• Разложение вейвлет-пакета
• Вейвлет-преобразование