Разложение вейвлет-пакета
Первоначально известное как оптимальное структурирование дерева поддиапазонов ( SB-TS ), также называемое вейвлет-разложением пакетов ( WPD ; иногда называемое просто вейвлет-пакетами или деревом поддиапазонов ), представляет собой вейвлет- преобразование, при котором дискретный (выборочный) сигнал проходит через большее количество фильтров. чем дискретное вейвлет-преобразование (DWT).
Введение
[ редактировать ]В DWT каждый уровень вычисляется путем передачи только предыдущих коэффициентов вейвлет-аппроксимации ( cA j нижних и верхних частот с дискретным временем ) через квадратурные зеркальные фильтры . [1] [2] Однако в WPD как детали ( cD j (в 1-D случае), cH j , cV j , cD j (в 2-D случае)) и коэффициенты аппроксимации разлагаются для создания полного двоичного дерева. [3] [2] [4] [5] [6] [7]
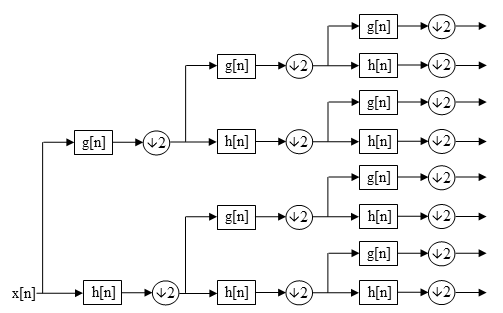
Для n уровней разложения WPD производит 2 н разные наборы коэффициентов (или узлов) в отличие от наборов ( n + 1) для DWT. Однако из-за процесса понижающей дискретизации общее количество коэффициентов остается прежним и избыточности нет.
С точки зрения сжатия стандартное вейвлет-преобразование может дать не лучший результат, поскольку оно ограничено базисами вейвлетов, увеличивающимися на степень двойки в сторону низких частот. Возможно, другая комбинация оснований дает более желательное представление для конкретного сигнала. [5] Существует несколько алгоритмов структурирования дерева поддиапазонов, которые находят набор оптимальных баз, обеспечивающих наиболее желательное представление данных относительно конкретной функции стоимости ( энтропии , сжатия энергии и т. д.). [1] [2] Были проведены соответствующие исследования в области обработки сигналов и связи для решения вопроса выбора деревьев поддиапазонов (ортогональный базис) различных типов, например, регулярных, диадических, нерегулярных, с учетом интересующих показателей производительности, включая сжатие энергии ( энтропию ), корреляции поддиапазонов и другие. . [4] [6] [7]
Теория дискретного вейвлет-преобразования (непрерывного по временной переменной) предлагает приближение для преобразования дискретных (выборочных) сигналов. Напротив, теория преобразования поддиапазонов с дискретным временем обеспечивает идеальное представление уже дискретизированных сигналов. [5] [8]
Галерея
[ редактировать ]- Пакетные функции Добеши D12
- Их спектры Фурье
Приложения
[ редактировать ]- Вейвлет-пакеты успешно применяются в доклинической диагностике. [9]
- Вейвлет-пакетное разложение оказывается полезным для регистрации сложных закономерностей и изменений электрохимических сигналов, которые могут указывать на состояние батареи и ее деградацию с течением времени. Разбивая сложный сигнал батареи на составляющие ее частотные компоненты, вейвлет-пакетное разложение позволяет провести более детальный анализ основных характеристик, связанных с различными стадиями старения батареи. [10]
- Вейвлет-пакетное разложение используется в качестве этапа предварительной обработки для разложения сигналов вибрации, полученных от редуктора ветряной турбины, на несколько частотных диапазонов, улавливая как высокочастотные, так и низкочастотные компоненты. Такое разложение позволяет извлечь важные характеристики, связанные с признаками неисправностей в различных масштабах, что позволяет провести более полный анализ состояния работоспособности коробки передач. Это помогает повысить точность и эффективность обнаружения и классификации неисправностей, особенно в сложной и критической области систем редукторов ветряных турбин. [11]
- В контексте прогнозирования осадков вейвлет-пакетное разложение оказывается ценным для выявления сложных и многомасштабных закономерностей в данных об осадках. Он может разложить исходный временной ряд месячных осадков на различные подряды, соответствующие разной частоте. Такое разложение помогает выявить скрытые закономерности и тенденции в данных, что может иметь решающее значение для повышения точности прогнозирования. [12]
- Обнаружение влаги в древесине имеет решающее значение для оценки ее структурной целостности и предотвращения потенциальных проблем, таких как гниение и повреждение. Вейвлет-пакетное разложение — это мощный метод обработки сигналов, который предлагает анализ содержания влаги в древесине с разными разрешениями. Этот подход позволяет детально изучить сигнал в разных диапазонах частот, обеспечивая более полное понимание распределения влаги внутри материала. [13]
- Исследователи используют вейвлет-пакетное разложение для анализа сейсмического отклика конструкций, что обеспечивает более точное разрешение как во временной, так и в частотной области. Этот подробный анализ позволяет выявить незначительные изменения в структурной реакции, которые могут указывать на повреждение. Разлагая сейсмический отклик на составляющие его частотные компоненты, исследователи получают представление об изменяющихся во времени характеристиках поведения конструкции. Это имеет решающее значение для выявления динамических изменений в реакции конструкции с течением времени, которые могут указывать на наличие и степень повреждения. [14]
- В контексте прогнозирования цен на фьючерсы на нефть характер вейвлет-пакетного разложения с несколькими разрешениями позволяет модели прогнозирования улавливать как высокочастотные, так и низкочастотные компоненты временного ряда, тем самым улучшая способность улавливать сложные закономерности и колебания, присущие финансовым данным. [15]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б Койфман Р.Р. и Викерхаузер М.В., 1992. Энтропийные алгоритмы для выбора наилучшего базиса , Транзакции IEEE по теории информации, 38 (2).
- ^ Перейти обратно: а б с А.Н. Акансу и Ю. Лю, О методах разложения сигналов (приглашенный доклад), Журнал оптической инженерии, специальный выпуск «Визуальные коммуникации и обработка изображений», том. 30, стр. 912–920, июль 1991 г.
- ^ Добеши, И. (1992), Десять лекций по вейвлетам, SIAM.
- ^ Перейти обратно: а б Х. Чаглар, Ю. Лю и А. Н. Акансу, Статистически оптимизированный дизайн PR-QMF , Proc. SPIE Визуальные коммуникации и обработка изображений, том. 1605, стр. 86–94, 1991.
- ^ Перейти обратно: а б с А.Н. Акансу и Р.А. Хаддад, Разложение сигнала с несколькими разрешениями: преобразования, поддиапазоны и вейвлеты . Бостон, Массачусетс: Академическая пресса, ISBN 978-0-12-047141-6 , 1992.
- ^ Перейти обратно: а б Беняссин А., Акансу А.Н. Анализ характеристик и оптимальное структурирование подканалов дискретных многотональных приемопередатчиков . Учеб. Международный симпозиум IEEE по схемам и системам (ISCAS), стр. 1456–1459, апрель 1995 г.
- ^ Перейти обратно: а б М. В. Тазебай и А. Н. Акансу, Адаптивные преобразования поддиапазонов в частотно-временных эксцайзерах для систем связи DSSS , IEEE Trans. Сигнальный процесс., вып. 43, стр. 2776–2782, ноябрь 1995 г.
- ^ А.Н. Акансу, В.А. Сердейн и И.В. Селесник, Вейвлет-преобразования при обработке сигналов: обзор новых приложений , Физическая связь, Elsevier, vol. 3, выпуск 1, стр. 1–18, март 2010 г.
- ^ Чжан, Ю.; Донг, З. (2015). «Доклиническая диагностика магнитно-резонансных (МР) изображений мозга с помощью дискретного вейвлет-пакетного преобразования с энтропией Тсаллиса и машиной проксимальных опорных векторов обобщенных собственных значений (GEPSVM)» . Энтропия . 17 (4): 1795–1813. Бибкод : 2015Entrp..17.1795Z . дои : 10.3390/e17041795 .
- ^ Дин, Пан; Лю, Сяоцзюань; Ли, Хуэйцинь; Хуан, Цзэцюань; Чжан, Кэ; Шао, Лонг; Абединиа, Овеис (2021). «Полезное предсказание срока службы на основе вейвлет-пакетного разложения и двумерной сверточной нейронной сети для литий-ионных батарей» . Обзоры возобновляемой и устойчивой энергетики . 148 . дои : 10.1016/j.rser.2021.111287 .
- ^ Хуанг, Д.; Чжан, В.-А.; Го, Ф.; Лю, В.; Ши, X. (12 ноября 2021 г.). «Многомасштабная CNN на основе разложения вейвлет-пакетов для диагностики неисправностей коробки передач ветряных турбин» . Транзакции IEEE по кибернетике . 53 (1): 443–453. дои : 10.1109/TCYB.2021.3123667 . ПМИД 34767518 .
- ^ Ван, В.; Ван, Ю.; Чау, К.; Лю, К.; Ма, К. (2021). «Сравнение BPNN, GMDH и ARIMA для ежемесячного прогнозирования количества осадков на основе разложения вейвлет-пакетов» . Вода . 13 (20): 2871. дои : 10.3390/w13202871 .
- ^ Юань, Ченг; Чжан, Цзичэн; Чен, Линь; Сюй, Цзя; Конг, Цинчжао (10 февраля 2021 г.). «Обнаружение влажности древесины с использованием вейвлет-пакетного разложения и сверточной нейронной сети» . Умные материалы и конструкции . 30 (3): 035022. Бибкод : 2021SMaS...30c5022Y . дои : 10.1088/1361-665X/abdc08 .
- ^ Он, Хаосян; Чен, Ифэй; Лан, Бинцзи (2021). «Оценка ущерба конструкции, подвергшейся землетрясению, с использованием вейвлет-пакетного разложения и изменяющейся во времени частоты» . Структуры . 34 : 449–461. doi : 10.1016/j.istruc.2021.07.087 .
- ^ Ван, Цзе; Ван, июнь (2021 г.). «Новая гибридная модель прогнозирования, основанная на SW-LSTM и вейвлет-пакетном разложении: пример цен на фьючерсы на нефть» . Вычислительный интеллект и нейронаука . 2021 : 1–22. дои : 10.1155/2021/7653091 . ПМК 8292043 . ПМИД 34335724 .
Внешние ссылки
[ редактировать ]- Реализацию вейвлет-пакетного разложения можно найти в наборе инструментов MATLAB wavelet .
- Реализацию для R можно найти в пакете wavethresh .
- Иллюстрацию и реализацию вейвлет-пакетов вместе с их кодом на C++ можно найти по адресу: Ян Каплан (март 2002 г.). «Вейвлет-пакетное преобразование» . Медвежья пещера .
- JWave : реализация на Java для 1-D и 2-D вейвлет-пакетов с использованием вейвлетов Haar , Daubechies , Coiflet и Legendre .

