Вейвлет Габора

Вейвлеты Габора — это вейвлеты, изобретенные Деннисом Габором с использованием сложных функций, созданных в качестве основы для преобразований Фурье в приложениях теории информации . Они очень похожи на вейвлеты Морле . Они также тесно связаны с фильтрами Габора . Важным свойством вейвлета является то, что он минимизирует произведение своих стандартных отклонений во временной и частотной области (задаваемое дисперсиями, определенными ниже). Другими словами, неопределенность информации, передаваемой этим вейвлетом, сводится к минимуму. Однако у них есть обратная сторона: они неортогональны, поэтому эффективная декомпозиция на базис затруднена. С момента их создания появились различные приложения — от обработки изображений до анализа нейронов зрительной системы человека. ^[1]^[2]

Свойство минимальной неопределенности

Мотивацией для вейвлетов Габора является поиск некоторой функции $f(x)$ что минимизирует его стандартное отклонение во временной и частотной областях. Более формально, дисперсия в области позиций равна:

(\Delta x)^{2}={\frac {\int _{-\infty }^{\infty }(x-\mu )^{2}f(x)f^{*}(x)\,dx}{\int _{-\infty }^{\infty }f(x)f^{*}(x)\,dx}}

где $f^{*}(x)$ является комплексно-сопряженным $f(x)$ и $\mu$ среднее арифметическое, определяемое как:

\mu ={\frac {\int _{-\infty }^{\infty }xf(x)f^{*}(x)\,dx}{\int _{-\infty }^{\infty }f(x)f^{*}(x)\,dx}}

Дисперсия в области волновых чисел равна:

(\Delta k)^{2}={\frac {\int _{-\infty }^{\infty }(k-k_{0})^{2}F(k)F^{*}(k)\,dk}{\int _{-\infty }^{\infty }F(k)F^{*}(k)\,dk}}

Где $k_{0}$ — среднее арифметическое преобразования Фурье $f(x)$ , $F(x)$ :

k_{0}={\frac {\int _{-\infty }^{\infty }kF(k)F^{*}(k)\,dk}{\int _{-\infty }^{\infty }F(k)F^{*}(k)\,dk}}

Если они определены, неопределенность записывается как:

(\Delta x)(\Delta k)

Было показано, что эта величина имеет нижнюю границу ${\frac {1}{2}}$ . Точка зрения квантовой механики заключается в интерпретации $(\Delta x)$ как неопределенность в положении и $\hbar (\Delta k)$ как неопределенность в импульсе. Функция $f(x)$ который имеет наименьшую теоретически возможную границу неопределенности, - это вейвлет Габора. ^[3]

Уравнение

Уравнение одномерного вейвлета Габора представляет собой гауссово уравнение, модулированное комплексной экспонентой, описываемое следующим образом: ^[3]

f(x)=e^{-(x-x_{0})^{2}/a^{2}}e^{-ik_{0}(x-x_{0})}

В отличие от других функций, обычно используемых в качестве баз в преобразованиях Фурье, таких как $\sin$ и $\cos$ , вейвлеты Габора обладают тем свойством, что они локализованы, а это означает, что по мере удаления от центра $x_{0}$ увеличивается, значение функции становится экспоненциально подавленным. $a$ контролирует скорость этого экспоненциального спада и $k_{0}$ контролирует скорость модуляции.

Также стоит отметить преобразование Фурье (унитарное соглашение по угловой частоте) вейвлета Габора, который также является вейвлетом Габора:

F(k)=ae^{-(k-k_{0})^{2}a^{2}}e^{-ix_{0}(k-k_{0})}

Пример вейвлета приведен здесь:

Вейвлет Габора с a = 2, x ₀ = 0 и k ₀ = 1

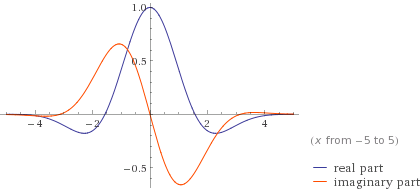
Временной аналог вейвлета Габора

При обработке временных сигналов доступ к данным из будущего невозможен, что приводит к проблемам при попытке использовать функции Габора для обработки сигналов реального времени, которые зависят от временного измерения. Временно-причинный аналог фильтра Габора был разработан в ^[4] основанный на замене ядра Гаусса в функции Габора ядром временно-каузального и время-рекурсивного сглаживания, называемым временем-каузальным предельным ядром. Таким образом, частотно-временной анализ, основанный на результирующем комплекснозначном расширении ядра причинно-временного предела, позволяет уловить по существу аналогичные преобразования временного сигнала, с которыми могут справиться вейвлеты Габора и соответствующие группе Гейзенберга, в то время как осуществляется с помощью строго времени-каузальных и время-рекурсивных операций, см. ^[4] для получения более подробной информации.

См. также

Ссылки

^ Ли, Тай С. (октябрь 1996 г.). «Представление изображения с использованием 2D-вейвлетов Габора» (PDF) . Транзакции IEEE по анализу шаблонов и машинному интеллекту . 18 (10): 959–971. дои : 10.1109/34.541406 .
^ Даугман, Джон. Серия лекций по компьютерному зрению (PDF) . Кембриджский университет.
^ Jump up to: ^а ^б Даугман, Джон. Серия лекций по теории информации (PDF) . Кембриджский университет.
^ Jump up to: ^а ^б Линдеберг, Т. (23 января 2023 г.). «Причинно-временное и рекурсивное во времени масштабно-пространственное представление временных сигналов и прошлого времени» . Биологическая кибернетика : 1–39. arXiv : 2202.09209 . дои : 10.1007/s00422-022-00953-6 .

Внешние ссылки

Код MATLAB для 2D вейвлетов Габора и извлечения признаков Габора

[imageRep-1] Ли, Тай С. (октябрь 1996 г.). «Представление изображения с использованием 2D-вейвлетов Габора» (PDF) . Транзакции IEEE по анализу шаблонов и машинному интеллекту . 18 (10): 959–971. дои : 10.1109/34.541406 .

[CVRef-2] Даугман, Джон. Серия лекций по компьютерному зрению (PDF) . Кембриджский университет.

[infRef-3] Jump up to: ^а ^б Даугман, Джон. Серия лекций по теории информации (PDF) . Кембриджский университет.

[Lin23-4] Jump up to: ^а ^б Линдеберг, Т. (23 января 2023 г.). «Причинно-временное и рекурсивное во времени масштабно-пространственное представление временных сигналов и прошлого времени» . Биологическая кибернетика : 1–39. arXiv : 2202.09209 . дои : 10.1007/s00422-022-00953-6 .

[1]

[2]

[3]

[4]