Вектор (математика и физика)

В математике и физике , вектор — это термин, неформально обозначающий некоторые величины которые не могут быть выражены одним числом ( скаляром ), или элементы некоторых векторных пространств .

Исторически векторы были введены в геометрию и физику (обычно в механику ) для величин, которые имеют как величину, так и направление, таких как перемещения , силы и скорость . Такие величины представляются геометрическими векторами так же, как расстояния , массы и время представляются действительными числами .

Термин вектор также используется в некоторых контекстах для кортежей , которые представляют собой конечные последовательности (числа или другие объекты) фиксированной длины.

Как геометрические векторы, так и кортежи можно складывать и масштабировать, и эти векторные операции привели к концепции векторного пространства, которое представляет собой множество, оснащенное векторным сложением и скалярным умножением , которое удовлетворяет некоторым аксиомам , обобщающим основные свойства вышеперечисленных операций. виды векторов. Векторное пространство, образованное геометрическими векторами, называется евклидовым векторным пространством , а векторное пространство, образованное кортежами, называется координатным векторным пространством .

В математике рассматриваются многие векторные пространства, такие как поля расширения , кольца полиномов , алгебры и функциональные пространства . Термин вектор обычно не используется для элементов этих векторных пространств и обычно зарезервирован для геометрических векторов, кортежей и элементов неопределенных векторных пространств (например, при обсуждении общих свойств векторных пространств).

в евклидовой геометрии Векторы

В математике , физике и технике или евклидов вектор просто вектор (иногда называемый геометрическим вектором). ^[1] или пространственный вектор ^[2]) — геометрический объект, имеющий величину (или длину ) и направление . Евклидовы векторы можно складывать и масштабировать для формирования векторного пространства . Евклидов вектор часто изображается в виде направленного отрезка линии или графически в виде стрелки, соединяющей точку А с конечной точкой В. начальную ^[3] и обозначается ${\textstyle {\stackrel {\longrightarrow }{AB}}.}$

Вектор — это то, что нужно, чтобы «перенести» точку А в точку Б ; латинское слово вектор означает «носитель». ^[4] Впервые его использовали астрономы XVIII века, исследующие вращение планет вокруг Солнца. ^[5] Величина вектора — это расстояние между двумя точками, а направление — это смещения от A до B. направление Многие алгебраические операции над действительными числами, такие как сложение , вычитание , умножение и отрицание , имеют близкие аналоги для векторов. ^[6] операции, подчиняющиеся известным алгебраическим законам коммутативности , ассоциативности и дистрибутивности . Эти операции и связанные с ними законы квалифицируют евклидовы векторы как пример более обобщенной концепции векторов, определяемых просто как элементы векторного пространства .

Векторы играют важную роль в физике : скорость и ускорение движущегося объекта, а также действующие на него силы можно описать векторами. ^[7] Многие другие физические величины можно рассматривать как векторы. Хотя большинство из них не представляют расстояния (за исключением, например, положения или смещения ), их величину и направление все же можно представить длиной и направлением стрелки. Математическое представление физического вектора зависит от системы координат, используемой для его описания. К другим вектороподобным объектам, описывающим физические величины и аналогичным образом преобразующимся при изменении системы координат, относятся псевдовекторы и тензоры . ^[8]

Векторные пространства [ править ]

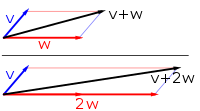
В математике и физике векторное пространство (также называемое линейным пространством) — это набор , элементы которого, часто называемые векторами , можно складывать и умножать («масштабировать») на числа, называемые скалярами . Скаляры часто являются действительными числами , но могут быть и комплексными числами или, в более общем плане, элементами любого поля . Операции сложения векторов и скалярного умножения должны удовлетворять определенным требованиям, называемым векторными аксиомами . Реальное векторное пространство и комплексное векторное пространство — это виды векторных пространств, основанные на различных видах скаляров: действительное координатное пространство или комплексное координатное пространство .

Векторные пространства обобщают евклидовы векторы , которые позволяют моделировать физические величины , такие как силы и скорость , которые имеют не только величину , но и направление . Концепция векторных пространств является фундаментальной для линейной алгебры вместе с концепцией матриц , которая позволяет выполнять вычисления в векторных пространствах. Это обеспечивает краткий и синтетический способ манипулирования и изучения систем линейных уравнений .

Векторные пространства характеризуются своей размерностью , которая, грубо говоря, задает количество независимых направлений в пространстве. Это означает, что для двух векторных пространств над данным полем и одинаковой размерности свойства, которые зависят только от структуры векторного пространства, совершенно одинаковы (технически векторные пространства изоморфны ) . Векторное пространство является конечномерным, если его размерность является натуральным числом . В противном случае оно бесконечномерно , а его размерность — бесконечный кардинал . Конечномерные векторные пространства естественным образом встречаются в геометрии и смежных областях. Бесконечномерные векторные пространства встречаются во многих областях математики. Например, кольца полиномов представляют собой счетно -бесконечномерные векторные пространства, а многие функциональные пространства имеют мощность континуума в качестве размерности.

Многие векторные пространства, рассматриваемые в математике, наделены и другими структурами . Это случай алгебр , которые включают расширения полей , кольца многочленов, ассоциативные алгебры и алгебры Ли . Это также относится к топологическим векторным пространствам , которые включают функциональные пространства, пространства внутреннего произведения , нормированные пространства , гильбертовы пространства и банаховы пространства .

Векторы в алгебре [ править ]

Любая алгебра над полем представляет собой векторное пространство, но элементы алгебры обычно не называются векторами. Однако в некоторых случаях их называют векторами , главным образом по историческим причинам.

Векторный кватернион , кватернион с нулевой вещественной частью.
Мультивектор или $p$ -вектор , элемент внешней алгебры векторного пространства.
Спиноры , также называемые векторами спина , были введены для расширения понятия вектора вращения . Фактически, векторы вращения представляют собой вращения скважин локально , а не глобально, поскольку замкнутый контур в пространстве векторов вращения может вызвать кривую в пространстве вращений, которая не является петлей. Кроме того, многообразие векторов вращения ориентируемо , а многообразие вращений — нет. Спиноры — это элементы векторного подпространства некоторой алгебры Клиффорда .
Вектор Витта — бесконечная последовательность элементов коммутативного кольца, которая принадлежит алгебре над этим кольцом и была введена для обработки распространения переноса в операциях над p-адическими числами .

Данные, представленные векторами [ править ]

Набор $\mathbb {R} ^{n}$ из кортежей действительных чисел $n$ имеет естественную структуру векторного пространства, определяемую покомпонентным сложением и скалярным умножением . Эти кортежи принято называть векторами , даже в тех контекстах, где операции с векторным пространством не применяются. В более общем смысле, когда некоторые данные могут быть естественным образом представлены векторами, их часто называют векторами, даже если сложение и скалярное умножение векторов не являются допустимыми операциями над этими данными. ^{[ оспаривается – обсуждаем ]} Вот несколько примеров.

Вектор вращения — евклидов вектор , направление которого совпадает с направлением оси вращения , а величина — это угол поворота.
Вектор Бюргерса — вектор, который представляет величину и направление искажения дислокаций в кристаллической решетке.
Интервальный вектор в теории музыкальных множеств — массив, выражающий интервальное содержимое набора высотных классов.
Вектор вероятности — в статистике вектор с неотрицательными элементами, сумма которых равна единице.
Случайный вектор или многомерная случайная величина , в статистике — набор действительных , случайных величин которые могут коррелировать . Однако случайный вектор может также относиться к случайной величине , которая принимает свои значения в векторном пространстве.
Логический вектор , вектор из 0 и 1 ( логические значения ).

Векторы в исчислении [ править ]

Исчисление служит основным математическим инструментом в области векторов, предлагая основу для анализа и манипулирования векторными величинами в различных научных дисциплинах, особенно в физике и технике . Векторные функции, где выходным сигналом является вектор, тщательно исследуются с помощью исчисления, чтобы получить важную информацию о движении в трехмерном пространстве. Векторное исчисление расширяет традиционные принципы исчисления на векторные поля, вводя такие операции, как градиент , дивергенция и ротор , которые находят применение в физике и инженерном контексте. Линейные интегралы , имеющие решающее значение для расчета работы на пути в силовых полях, и поверхностные интегралы , используемые для определения таких величин, как поток , иллюстрируют практическую полезность исчисления в векторном анализе. Интегралы по объему , необходимые для вычислений, включающих скалярные или векторные поля в трехмерных областях, способствуют пониманию распределения массы , плотности заряда и скорости потока жидкости. ^{[ нужна ссылка ]}

См. также [ править ]

Вектор (значения)

пространства с структурой большей Векторные

Градуированное векторное пространство — тип векторного пространства, включающий дополнительную структуру градации.
Нормированное векторное пространство — векторное пространство, в котором определена норма.
Гильбертово пространство
Упорядоченное векторное пространство — векторное пространство, обладающее частичным порядком.
Супервекторное пространство , название _{Z 2.} векторного пространства, градуированного по
Симплектическое векторное пространство , векторное пространство V, снабженное невырожденной кососимметричной билинейной формой.
Топологическое векторное пространство , смесь топологической структуры с алгебраической концепцией векторного пространства.

Векторные поля [ править ]

Векторное поле — это векторная функция , которая, как правило, имеет область той же размерности (как многообразие ), что и ее кодомен,

Консервативное векторное поле — векторное поле, представляющее собой градиент скалярного потенциального поля.
Векторное поле Гамильтона — векторное поле, определенное для любой энергетической функции или гамильтониана.
Векторное поле Киллинга — векторное поле на римановом многообразии.
Соленоидальное векторное поле — векторное поле с нулевой дивергенцией.
Векторный потенциал — векторное поле, ротор которого является заданным векторным полем.
Векторный поток , набор тесно связанных понятий потока, определяемого векторным полем.

Разное [ править ]

Фигурное исчисление
Векторный анализ , учебник Уилсона по векторному исчислению , впервые опубликованный в 1901 году, который во многом способствовал стандартизации обозначений и словаря трехмерной линейной алгебры и векторного исчисления.
Векторное расслоение — топологическая конструкция, которая уточняет идею семейства векторных пространств, параметризованных другим пространством.
Векторное исчисление — раздел математики, занимающийся дифференцированием и интегрированием векторных полей.
Векторный дифференциал , или del , оператор векторного дифференциала, представленный символом набла. $\nabla$
Вектор Лапласа , векторный оператор Лапласа, обозначаемый $\nabla ^{2}$ , — дифференциальный оператор, определенный над векторным полем
Векторные обозначения , распространенные обозначения, используемые при работе с векторами.
Векторный оператор — тип дифференциального оператора, используемый в векторном исчислении.
Векторное произведение или векторное произведение — операция над двумя векторами в трехмерном евклидовом пространстве, в результате которой получается третий трехмерный евклидов вектор, перпендикулярный двум исходным.
Векторная проекция , также известная как векторная резолюция или компонент вектора , линейное отображение, создающее вектор, параллельный второму вектору.
Векторнозначная функция — функция , имеющая векторное пространство в качестве кодомена.
Векторизация (математика) — линейное преобразование, преобразующее матрицу в вектор-столбец.
Векторная авторегрессия — эконометрическая модель, используемая для отражения эволюции и взаимозависимостей между несколькими временными рядами.
Векторный бозон — бозон со спиновым квантовым числом, равным 1.
Векторная мера — функция, определенная в семействе множеств и принимающая векторные значения, удовлетворяющие определенным свойствам.
Векторный мезон — мезон с полным спином 1 и нечетной четностью.
Векторное квантование — метод квантования, используемый при обработке сигналов.
Векторный солитон — уединенная волна, состоящая из нескольких компонентов, связанных вместе, которая сохраняет свою форму во время распространения.
Векторный синтез — разновидность синтеза звука.
Фазовый вектор

Примечания [ править ]

^ Иванов 2001.
^ Хайнбокель 2001
^ Ито 1993 , стр. 1678 ;
^ Латынь: vectus, причастие совершенного вида от vehere, «нести» / veho = «Я несу». Об историческом развитии слова вектор см. «вектор н. » . Оксфордский словарь английского языка (онлайн-изд.). Издательство Оксфордского университета . (Требуется подписка или членство в участвующей организации .) и Джефф Миллер. «Самые ранние известные варианты использования некоторых математических слов» . Проверено 25 мая 2007 г.
^ Оксфордский словарь английского языка (2-е изд.). Лондон: Кларендон Пресс. 2001. ISBN 9780195219425 .
^ «вектор | Определение и факты» . Британская энциклопедия . Проверено 19 августа 2020 г.
^ «Векторы» . www.mathsisfun.com . Проверено 19 августа 2020 г.
^ Вайсштейн, Эрик В. «Вектор» . mathworld.wolfram.com . Проверено 19 августа 2020 г.

Ссылки [ править ]

Векторы - Фейнмановские лекции по физике
Хайнбокель, Дж. Х. (2001). Введение в тензорное исчисление и механику сплошных сред . Траффорд Паблишинг. ISBN 1-55369-133-4 .
Ито, Кийоси (1993). Энциклопедический математический словарь (2-е изд.). МТИ Пресс . ISBN 978-0-262-59020-4 .
Иванов, А.Б. (2001) [1994], «Вектор» , Энциклопедия Математики , EMS Press
Педо, Дэниел (1988). Геометрия: Комплексный курс . Дувр. ISBN 0-486-65812-0 .

[1] Иванов 2001.

[2] Хайнбокель 2001

[3] Ито 1993 , стр. 1678 ;

[4] Латынь: vectus, причастие совершенного вида от vehere, «нести» / veho = «Я несу». Об историческом развитии слова вектор см. «вектор н. » . Оксфордский словарь английского языка (онлайн-изд.). Издательство Оксфордского университета . (Требуется подписка или членство в участвующей организации .) и Джефф Миллер. «Самые ранние известные варианты использования некоторых математических слов» . Проверено 25 мая 2007 г.

[5] Оксфордский словарь английского языка (2-е изд.). Лондон: Кларендон Пресс. 2001. ISBN 9780195219425 .

[Euclidean_vector_:1-6] «вектор | Определение и факты» . Британская энциклопедия . Проверено 19 августа 2020 г.

[Euclidean_vector_:2-7] «Векторы» . www.mathsisfun.com . Проверено 19 августа 2020 г.

[8] Вайсштейн, Эрик В. «Вектор» . mathworld.wolfram.com . Проверено 19 августа 2020 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]