Перекрестное произведение

Эта статья о векторном произведении двух векторов в трехмерном евклидовом пространстве. Чтобы узнать о других значениях, см. Перекрестное произведение (значения) .

Перекрестное произведение относительно правой системы координат

В математике векторное произведение или векторное произведение (иногда произведение направленной площади , чтобы подчеркнуть его геометрическое значение) — это бинарная операция над двумя векторами в трехмерном ориентированном евклидовом векторном пространстве (названном здесь $E$) и обозначается символом $\times$. Учитывая два линейно независимых вектора a и b , векторное произведение a × b (читай «крест b») представляет собой вектор, который перпендикулярен как a, так и b , и, таким образом, нормальны к плоскости, содержащей их. Он имеет множество приложений в математике, физике , технике и компьютерном программировании . Его не следует путать со скалярным произведением (проекционным произведением).

Величина векторного произведения равна площади параллелограмма с векторами сторон; в частности, величина произведения двух перпендикулярных векторов равна произведению их длин. Единицы . векторного произведения являются произведением единиц каждого вектора Если два вектора параллельны или антипараллельны (то есть линейно зависимы) или любой из них имеет нулевую длину, то их векторное произведение равно нулю.

Перекрестное произведение является антикоммутативным (то есть a × b = − b × a ) и дистрибутивным по сложению, то есть a × ( b + c ) = a × b + a × c . Пространство $E$ вместе с векторным произведением представляет собой алгебру над действительными числами , которая не является ни коммутативной , ни ассоциативной , но является алгеброй Ли , векторное произведение которой является скобкой Ли .

Как и скалярное произведение, оно зависит от метрики евклидова пространства , но в отличие от скалярного произведения оно также зависит от выбора ориентации ( или « направленности ») пространства (именно поэтому и необходимо ориентированное пространство). Результирующий вектор является инвариантом вращения базиса. Из-за зависимости от направленности векторное произведение называется псевдовектором .

Что касается векторного произведения, внешнее произведение векторов может использоваться в произвольных измерениях (с результатом бивектора или 2-формы ) и не зависит от ориентации пространства.

Продукт можно обобщить различными способами, используя ориентацию и метрическую структуру, как и для традиционного трехмерного векторного произведения: в n измерениях можно взять произведение n - 1 векторов, чтобы получить вектор, перпендикулярный всем им. . Но если продукт ограничивается нетривиальными двоичными продуктами с векторными результатами, он существует только в трех и семи измерениях. Однако векторное произведение в семи измерениях имеет нежелательные свойства (например, оно не удовлетворяет тождеству Якоби ), поэтому оно не используется в математической физике для представления таких величин, как многомерное пространство-время . ( разделе «Обобщения» Другие измерения см. в ниже.)

Определение

Нахождение направления векторного произведения по правилу правой руки

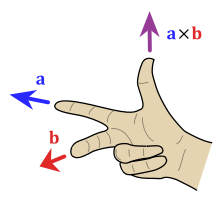
Взаимное произведение двух векторов a и b определяется только в трехмерном пространстве и обозначается a × b . В физике и прикладной математике часто используется клиновое обозначение a ∧ b (вместе с названием векторного произведения ), хотя в чистой математике такое обозначение обычно применяется только для внешнего произведения, абстракции векторного произведения до n измерений.

Векторное произведение a × b определяется как вектор c , который перпендикулярен (ортогонален) как a, так и b , с направлением, заданным правилом правой руки. и величину, равную площади параллелограмма , охватываемого векторами.

Перекрестное произведение определяется по формуле

$\mathbf {a} \times \mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\sin(\theta )\,\mathbf {n} ,$

где

θ - угол между a и b в плоскости, содержащей их (следовательно, он составляет от 0 ° до 180 °),

‖ a ‖ и ‖ b ‖ — величины векторов a и b ,

n — единичный вектор, перпендикулярный плоскости, содержащей a и b , с таким направлением, что упорядоченный набор ( a , b , n ) ориентирован положительно .

Если векторы a и b параллельны (то есть угол θ между ними равен 0° или 180°), по приведенной выше формуле векторное произведение a и b представляет собой нулевой вектор 0 .

Направление

Перекрестное произведение a × b (по вертикали, фиолетового цвета) изменяется при изменении угла между векторами a (синий) и b (красный). Векторное произведение всегда ортогонально обоим векторам и имеет нулевую величину, когда векторы параллельны, и максимальную величину ‖ a ‖‖ b ‖, когда они ортогональны.

Направление вектора n зависит от выбранной ориентации пространства. Традиционно это определяется правилом правой руки, когда нужно просто указать указательным пальцем правой руки в направлении a, а средним пальцем в направлении b . Затем вектор n выходит из большого пальца (см. рисунок рядом). Использование этого правила подразумевает, что векторное произведение антикоммутативно ; то есть б × а = -( а × б ) . Если сначала указать указательный палец на b , а затем средний палец на a , большой палец будет вынужден двигаться в противоположном направлении, меняя знак вектора произведения.

Поскольку оператор векторного произведения зависит от ориентации пространства, обычно векторное произведение двух векторов является не «истинным» вектором, а псевдовектором . см . в разделе «Рукость» Более подробную информацию .

Имена и происхождение

Согласно правилу Сарруса , определитель матрицы 3×3 включает в себя умножения между элементами матрицы, определяемыми скрещенными диагоналями.

В 1842 году Уильям Роуэн Гамильтон впервые описал алгебру кватернионов и некоммутативное произведение Гамильтона. В частности, когда выполняется гамильтоновское произведение двух векторов (то есть чистых кватернионов с нулевой скалярной частью), в результате получается кватернион со скалярной и векторной частью. Скалярная и векторная часть этого произведения Гамильтона соответствует отрицательному скалярному произведению и векторному произведению двух векторов.

В 1881 году Джозайя Уиллард Гиббс и независимо Оливер Хевисайд ввел обозначения как для скалярного произведения, так и для векторного произведения, используя для их обозначения период ( a ⋅ b ) и «×» ( a × b ) соответственно.

В 1877 году, чтобы подчеркнуть тот факт, что результатом скалярного произведения является скаляр , а результатом векторного произведения является вектор , Уильям Кингдон Клиффорд придумал альтернативные названия скалярное произведение и векторное произведение для этих двух операций. Эти альтернативные названия до сих пор широко используются в литературе.

И перекрестное обозначение ( a × b ), и название перекрестного произведения , возможно, были вдохновлены тем фактом, что каждый скалярный компонент a × b вычисляется путем умножения несоответствующих компонентов a и b . И наоборот, скалярное произведение a ⋅ b включает в себя умножение между соответствующими компонентами a и b . Как поясняется ниже , векторное произведение можно выразить в виде определителя специальной матрицы 3×3 . Согласно правилу Сарруса , это предполагает умножение между элементами матрицы, обозначенными скрещенными диагоналями.

Вычисление

Координатные обозначения

Стандартные базисные векторы ( i , j , k , также обозначаются e ₁ , e ₂ , e ₃ ) и компоненты a , ( a _x , a _y , a _z , также обозначаются a ₁ , a ₂ векторные a ₃ )

Если ( i , j , k ) положительно ориентированный ортонормированный базис, базисные векторы удовлетворяют следующим равенствам

${\begin{alignedat}{2}\mathbf {\color {blue}{i}} &\times \mathbf {\color {red}{j}} &&=\mathbf {\color {green}{k}} \\\mathbf {\color {red}{j}} &\times \mathbf {\color {green}{k}} &&=\mathbf {\color {blue}{i}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {blue}{i}} &&=\mathbf {\color {red}{j}} \end{alignedat}}$

из чего следует, что в силу антикоммутативности векторного произведения

${\begin{alignedat}{2}\mathbf {\color {red}{j}} &\times \mathbf {\color {blue}{i}} &&=-\mathbf {\color {green}{k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\\mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}$

Антикоммутативность векторного произведения (и очевидное отсутствие линейной независимости) также означает, что

$\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} =\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} =\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} =\mathbf {0}$ ( нулевой вектор ).

Этих равенств, вместе с дистрибутивностью и линейностью векторного произведения (хотя ни то, ни другое легко не следует из определения, данного выше), достаточно для определения векторного произведения любых двух векторов a и b . Каждый вектор можно определить как сумму трех ортогональных компонентов, параллельных стандартным базисным векторам:

${\begin{alignedat}{3}\mathbf {a} &=a_{1}\mathbf {\color {blue}{i}} &&+a_{2}\mathbf {\color {red}{j}} &&+a_{3}\mathbf {\color {green}{k}} \\\mathbf {b} &=b_{1}\mathbf {\color {blue}{i}} &&+b_{2}\mathbf {\color {red}{j}} &&+b_{3}\mathbf {\color {green}{k}} \end{alignedat}}$

Их векторное произведение a × b можно разложить с помощью дистрибутивности:

${\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&(a_{1}\mathbf {\color {blue}{i}} +a_{2}\mathbf {\color {red}{j}} +a_{3}\mathbf {\color {green}{k}} )\times (b_{1}\mathbf {\color {blue}{i}} +b_{2}\mathbf {\color {red}{j}} +b_{3}\mathbf {\color {green}{k}} )\\={}&a_{1}b_{1}(\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} )+a_{1}b_{2}(\mathbf {\color {blue}{i}} \times \mathbf {\color {red}{j}} )+a_{1}b_{3}(\mathbf {\color {blue}{i}} \times \mathbf {\color {green}{k}} )+{}\\&a_{2}b_{1}(\mathbf {\color {red}{j}} \times \mathbf {\color {blue}{i}} )+a_{2}b_{2}(\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} )+a_{2}b_{3}(\mathbf {\color {red}{j}} \times \mathbf {\color {green}{k}} )+{}\\&a_{3}b_{1}(\mathbf {\color {green}{k}} \times \mathbf {\color {blue}{i}} )+a_{3}b_{2}(\mathbf {\color {green}{k}} \times \mathbf {\color {red}{j}} )+a_{3}b_{3}(\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} )\\\end{aligned}}$

Это можно интерпретировать как разложение a × b в сумму девяти более простых векторных произведений, включающих векторы, выровненные по i , j или k . Каждое из этих девяти векторных произведений оперирует двумя векторами, с которыми легко обращаться, поскольку они либо параллельны, либо ортогональны друг другу. В результате этого разложения, используя вышеупомянутые равенства и собирая аналогичные члены, мы получаем:

${\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&\quad \ a_{1}b_{1}\mathbf {0} +a_{1}b_{2}\mathbf {\color {green}{k}} -a_{1}b_{3}\mathbf {\color {red}{j}} \\&-a_{2}b_{1}\mathbf {\color {green}{k}} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {\color {blue}{i}} \\&+a_{3}b_{1}\mathbf {\color {red}{j}} \ -a_{3}b_{2}\mathbf {\color {blue}{i}} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {\color {blue}{i}} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {\color {red}{j}} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {\color {green}{k}} \\\end{aligned}}$

это означает, что три скалярные компоненты результирующего вектора s = s ₁ i + s ₂ j + s ₃ k = a × b равны

${\begin{aligned}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\\s_{2}&=a_{3}b_{1}-a_{1}b_{3}\\s_{3}&=a_{1}b_{2}-a_{2}b_{1}\end{aligned}}$

Используя векторы-столбцы , мы можем представить тот же результат следующим образом:

${\begin{bmatrix}s_{1}\\s_{2}\\s_{3}\end{bmatrix}}={\begin{bmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{bmatrix}}$

Матричное обозначение

Использование правила Сарруса для нахождения векторного произведения a и b.

Перекрестное произведение также можно выразить как формальный определитель:

$\mathbf {a\times b} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}$

Этот определитель можно вычислить с помощью правила Сарруса или разложения кофакторов . Используя правило Сарруса, оно расширяется до

${\begin{aligned}\mathbf {a\times b} &=(a_{2}b_{3}\mathbf {i} +a_{3}b_{1}\mathbf {j} +a_{1}b_{2}\mathbf {k} )-(a_{3}b_{2}\mathbf {i} +a_{1}b_{3}\mathbf {j} +a_{2}b_{1}\mathbf {k} )\\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} .\end{aligned}}$

что непосредственно дает компоненты результирующего вектора.

Использование тензоров Леви-Чивита

• В любом базисе перекрестное произведение $a\times b$ задается тензорной формулой $E_{ijk}a^{i}b^{j}$ где $E_{ijk}$ – ковариантный тензор Леви-Чивита (обратим внимание на положение индексов). Это соответствует внутренней формуле, приведенной здесь .
• В ортонормированном базисе, имеющем ту же ориентацию, что и пространство , $a\times b$ задается псевдотензорной формулой $\varepsilon _{ijk}a^{i}b^{j}$ где $\varepsilon _{ijk}$ – символ Леви-Чивита (который является псевдотензором). Это формула, используемая в повседневной физике, но она работает только для этого особого выбора базиса.
• В любом ортонормированном базисе $a\times b$ задается псевдотензорной формулой $(-1)^{B}\varepsilon _{ijk}a^{i}b^{j}$ где $(-1)^{B}=\pm 1$ указывает, имеет ли основание ту же ориентацию, что и пространство, или нет.

Последняя формула позволяет избежать необходимости менять ориентацию пространства при инвертировании ортонормированного базиса.

Характеристики

Геометрический смысл

См. Также: Тройной продукт

Рисунок 1. Площадь параллелограмма как величина векторного произведения

Рисунок 2. Три вектора, определяющие параллелепипед

Величину (см. рисунок 1 ): векторного произведения можно интерпретировать как положительную площадь параллелограмма , имеющего a и b стороны $$\left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|.$$

Действительно, можно также вычислить объем V параллелепипеда, имеющего ребра a , b и c , используя комбинацию векторного и скалярного произведения, называемого скалярным тройным произведением (см. рисунок 2):

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).$

Поскольку результат скалярного тройного произведения может быть отрицательным, объем параллелепипеда определяется его абсолютным значением:

$V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|.$

Поскольку величина векторного произведения определяется синусом угла между его аргументами, векторное произведение можно рассматривать как меру перпендикулярности точно так же, как скалярное произведение является мерой параллелизма . Учитывая два единичных вектора , их векторное произведение имеет величину 1, если они перпендикулярны, и нулевую величину, если они параллельны. Скалярное произведение двух единичных векторов ведет себя прямо противоположно: оно равно нулю, когда единичные векторы перпендикулярны, и 1, если единичные векторы параллельны.

Единичные векторы допускают два удобных тождества: скалярное произведение двух единичных векторов дает косинус (который может быть положительным или отрицательным) угла между двумя единичными векторами. Величина векторного произведения двух единичных векторов дает синус (который всегда будет положительным).

Алгебраические свойства

перекрестного произведения Скалярное умножение . Слева: Разложение b на компоненты, параллельные и перпендикулярные a . Справа: масштабирование перпендикулярных компонентов на положительное действительное число r (если оно отрицательное, b и векторное произведение меняются местами).

Распределение перекрестного произведения при сложении векторов. Слева: векторы b и c разлагаются на параллельные и перпендикулярные компоненты a . Справа: параллельные компоненты исчезают в векторном произведении, остаются только перпендикулярные компоненты, показанные в плоскости, перпендикулярной a .

Два неэквивалентных тройных векторных произведения трех векторов a , b , c . В каждом случае два вектора определяют плоскость, другой находится вне плоскости и может быть разделен на параллельные и перпендикулярные компоненты векторному произведению векторов, определяющих плоскость. Эти компоненты можно найти методами векторной проекции и отклонения . Тройное произведение находится в плоскости и вращается, как показано.

Если векторное произведение двух векторов является нулевым вектором (то есть a × b = 0 ), то либо один, либо оба входных параметра являются нулевым вектором ( a = 0 или b = 0 ), либо они параллельны, либо антипараллельны ( a ∥ b ) так, что синус угла между ними равен нулю ( θ = 0° или θ = 180° и sin θ = 0 ).

Самоперекрестное произведение вектора является нулевым вектором:

$\mathbf {a} \times \mathbf {a} =\mathbf {0} .$

Перекрестное произведение антикоммутативно ,

$\mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} ),$

дистрибутив над сложением,

$\mathbf {a} \times (\mathbf {b} +\mathbf {c} )=(\mathbf {a} \times \mathbf {b} )+(\mathbf {a} \times \mathbf {c} ),$

и совместим со скалярным умножением, так что

$(r\,\mathbf {a} )\times \mathbf {b} =\mathbf {a} \times (r\,\mathbf {b} )=r\,(\mathbf {a} \times \mathbf {b} ).$

Оно не ассоциативно , но удовлетворяет тождеству Якоби :

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )+\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0} .$

Дистрибутивность, линейность и тождество Якоби показывают, что R ³ векторное пространство вместе с векторным сложением и векторным произведением образует алгебру Ли , алгебру Ли вещественной ортогональной группы в трех измерениях, SO(3) .Перекрестное произведение не подчиняется закону сокращения ; то есть a × b = a × c с a ≠ 0 не подразумевает b = c , а только то, что:

${\begin{aligned}\mathbf {0} &=(\mathbf {a} \times \mathbf {b} )-(\mathbf {a} \times \mathbf {c} )\\&=\mathbf {a} \times (\mathbf {b} -\mathbf {c} ).\\\end{aligned}}$

Это может быть тот случай, когда b и c сокращаются, но, кроме того, когда a и b − c параллельны; то есть они связаны масштабным коэффициентом t , что приводит к:

$\mathbf {c} =\mathbf {b} +t\,\mathbf {a} ,$

для некоторого скалярного t .

Если в дополнение к a × b = a × c и a ≠ 0 , как указано выше, имеет место a ⋅ b = a ⋅ c , то

${\begin{aligned}\mathbf {a} \times (\mathbf {b} -\mathbf {c} )&=\mathbf {0} \\\mathbf {a} \cdot (\mathbf {b} -\mathbf {c} )&=0,\end{aligned}}$

Поскольку b - c не может быть одновременно параллельным (чтобы векторное произведение было равно 0 ) и перпендикулярно (чтобы скалярное произведение было равно 0) к a , должно быть так, что b и c сокращаются: b = c .

По геометрическому определению векторное произведение инвариантно относительно собственных вращений вокруг оси, определяемой a × b . В формулах:

$(R\mathbf {a} )\times (R\mathbf {b} )=R(\mathbf {a} \times \mathbf {b} )$, где $R$ представляет собой матрицу вращения с $\det(R)=1$.

В более общем смысле векторное произведение подчиняется следующему тождеству при матричных преобразованиях:

$(M\mathbf {a} )\times (M\mathbf {b} )=(\det M)\left(M^{-1}\right)^{\mathrm {T} }(\mathbf {a} \times \mathbf {b} )=\operatorname {cof} M(\mathbf {a} \times \mathbf {b} )$

где $M$ 3х3 представляет собой матрицу и $\left(M^{-1}\right)^{\mathrm {T} }$ является транспонированием обратного ​ и $\operatorname {cof}$ - матрица кофактора. Легко видеть, как эта формула сводится к первой, если $M$ представляет собой матрицу вращения. Если $M$ представляет собой симметричную матрицу 3х3, примененную к общему векторному произведению $\mathbf {a} \times \mathbf {b}$, справедливо следующее соотношение:

$M(\mathbf {a} \times \mathbf {b} )=\operatorname {Tr} (M)(\mathbf {a} \times \mathbf {b} )-\mathbf {a} \times M\mathbf {b} +\mathbf {b} \times M\mathbf {a}$

Перекрестное произведение двух векторов лежит в нулевом пространстве матрицы 2 × 3 , где векторы представляют собой строки:

$\mathbf {a} \times \mathbf {b} \in NS\left({\begin{bmatrix}\mathbf {a} \\\mathbf {b} \end{bmatrix}}\right).$

Для суммы двух векторных произведений справедливо следующее тождество:

$\mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} .$

Дифференциация

Основная статья: Векторнозначная функция § Производная и векторное умножение

Правило произведения дифференциального исчисления применимо к любой билинейной операции, а следовательно, и к векторному произведению:

${\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}},$

где a и b — векторы, которые зависят от действительной переменной t .

Тройное расширение продукта

Основная статья: Тройной продукт

Перекрестное произведение используется в обеих формах тройного произведения. Скалярное тройное произведение трех векторов определяется как

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ),$

Это объем параллелепипеда со знаком с ребрами a , b и c , и поэтому векторы можно использовать в любом порядке, который является четной перестановкой указанного выше порядка. Следовательно, следующие значения равны:

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ),$

представляет Тройное произведение вектора собой векторное произведение вектора на результат другого векторного произведения и связано со скалярным произведением по следующей формуле:

${\begin{aligned}\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )\\(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-\mathbf {a} (\mathbf {b} \cdot \mathbf {c} )\end{aligned}}$

Мнемоника « BAC минус CAB» используется для запоминания порядка векторов в правом члене. Эта формула используется в физике для упрощения векторных вычислений. Особый случай, касающийся градиентов и полезный в векторном исчислении , — это

${\begin{aligned}\nabla \times (\nabla \times \mathbf {f} )&=\nabla (\nabla \cdot \mathbf {f} )-(\nabla \cdot \nabla )\mathbf {f} \\&=\nabla (\nabla \cdot \mathbf {f} )-\nabla ^{2}\mathbf {f} ,\\\end{aligned}}$

где ∇ ² — векторный оператор Лапласа .

Другие тождества связывают векторное произведение со скалярным тройным произведением:

${\begin{aligned}(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )&=(\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ))\mathbf {a} \\(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )&=\mathbf {b} ^{\mathrm {T} }\left(\left(\mathbf {c} ^{\mathrm {T} }\mathbf {a} \right)I-\mathbf {c} \mathbf {a} ^{\mathrm {T} }\right)\mathbf {d} \\&=(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )\end{aligned}}$

где I — единичная матрица.

Альтернативная формулировка

Перекрестное произведение и скалярное произведение связаны соотношением:

$\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.$

Правая часть — это Грама a b и определитель , квадрат площади параллелограмма, определенного векторами. Это условие определяет величину векторного произведения. А именно, поскольку скалярное произведение определяется через угол θ между двумя векторами как:

$\mathbf {a\cdot b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta ,$

приведенное выше соотношение можно переписать следующим образом:

$\left\|\mathbf {a\times b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}\left(1-\cos ^{2}\theta \right).$

Применяя тригонометрическое тождество Пифагора, получаем:

$\left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|,$

который представляет собой величину векторного произведения, выраженного через θ , равную площади параллелограмма, определяемого a и b (см. определение выше).

Сочетание этого требования и того свойства, что векторное произведение ортогонально своим составляющим a и b, обеспечивает альтернативное определение векторного произведения.

Перекрестное произведение обратное

Для векторного произведения a × b = c существует несколько векторов b , которые дают одно и то же значение c . В результате невозможно перестроить это уравнение, чтобы получить уникальное решение для b через a и c . Тем не менее, можно найти семейство решений для b , которые

$\mathbf {b} ={\frac {\mathbf {c} \times \mathbf {a} }{\left\|\mathbf {a} \right\|^{2}}}+t\mathbf {a} ,$

где t — произвольная константа.

Это можно получить с помощью тройного разложения произведения:

$\mathbf {c} \times \mathbf {a} =(\mathbf {a} \times \mathbf {b} )\times \mathbf {a} =\left\|\mathbf {a} \right\|^{2}\mathbf {b} -(\mathbf {a} \cdot \mathbf {b} )\mathbf {a}$

Переставить, чтобы решить для b, чтобы получить

$\mathbf {b} ={\frac {\mathbf {c} \times \mathbf {a} }{\left\|\mathbf {a} \right\|^{2}}}+{\frac {\mathbf {a} \cdot \mathbf {b} }{\left\|\mathbf {a} \right\|^{2}}}\mathbf {a}$

Коэффициент последнего члена можно упростить до произвольной константы t, чтобы получить результат, показанный выше.

Личность Лагранжа

Отношение

$\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}\equiv \det {\begin{bmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{bmatrix}}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}$

можно сравнить с другим соотношением, включающим правую часть, а именно с тождеством Лагранжа, выраженным как

$\sum _{1\leq i<j\leq n}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a\cdot b} )^{2},$

где a и b могут быть n -мерными векторами. Это также показывает, что риманова форма объема поверхностей является в точности элементом поверхности из векторного исчисления. В случае, когда n = 3 , объединение этих двух уравнений приводит к выражению величины векторного произведения через его компоненты:

${\begin{aligned}\|\mathbf {a} \times \mathbf {b} \|^{2}&\equiv \sum _{1\leq i<j\leq 3}(a_{i}b_{j}-a_{j}b_{i})^{2}\\&\equiv (a_{1}b_{2}-b_{1}a_{2})^{2}+(a_{2}b_{3}-a_{3}b_{2})^{2}+(a_{3}b_{1}-a_{1}b_{3})^{2}.\end{aligned}}$

Тот же результат получается непосредственно с использованием компонентов векторного произведения, найденного из

$\mathbf {a} \times \mathbf {b} \equiv \det {\begin{bmatrix}{\hat {\mathbf {i} }}&{\hat {\mathbf {j} }}&{\hat {\mathbf {k} }}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{bmatrix}}.$

В Р ³ , уравнение Лагранжа является частным случаем мультипликативности | Фольксваген | = | в || ш | нормы в алгебре кватернионов .

Это частный случай другой формулы, также иногда называемой тождеством Лагранжа, которая представляет собой трехмерный случай тождества Бине-Коши :

$(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )\equiv (\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} ).$

Если a = c и b = d , это упрощается до приведенной выше формулы.

Бесконечно малые генераторы вращений

Дополнительная информация: Инфинитезимальная матрица вращения § Генераторы вращений.

Векторное произведение удобно описывает бесконечно малые генераторы вращений в R ³ . В частности, если n — единичный вектор в R ³ и R ( φ , n ) обозначает вращение вокруг оси через начало координат, указанное n , с углом φ (измеряется в радианах, против часовой стрелки, если смотреть с кончика n ), тогда

$\left.{d \over d\phi }\right|_{\phi =0}R(\phi ,{\boldsymbol {n}}){\boldsymbol {x}}={\boldsymbol {n}}\times {\boldsymbol {x}}$

для каждого вектора x в R ³ . Таким образом, векторное произведение на n описывает бесконечно малый генератор вращений вокруг n . Эти бесконечно малые генераторы образуют алгебру Ли so (3) группы вращений SO(3) , и мы получаем результат, что алгебра Ли R ³ с векторным произведением изоморфна алгебре Ли, поэтому (3).

Альтернативные способы расчета

Преобразование в матричное умножение

Векторное векторное произведение также можно выразить как произведение кососимметричной матрицы и вектора: $${\begin{aligned}\mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b} &={\begin{bmatrix}\,0&\!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}\\\mathbf {a} \times \mathbf {b} ={[\mathbf {b} ]_{\times }}^{\mathrm {\!\!T} }\mathbf {a} &={\begin{bmatrix}\,0&\,\,b_{3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}},\end{aligned}}$$где верхний индекс ^Т относится к операции транспонирования , а [ a ] _​​× определяется следующим образом: $$[\mathbf {a} ]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}.$$

Столбцы [ a ] _​​×,i кососимметричной матрицы для вектора a также могут быть получены путем вычисления векторного произведения с единичными векторами . То есть, $$[\mathbf {a} ]_{\times ,i}=\mathbf {a} \times \mathbf {{\hat {e}}_{i}} ,\;i\in \{1,2,3\}$$или $$[\mathbf {a} ]_{\times }=\sum _{i=1}^{3}\left(\mathbf {a} \times \mathbf {{\hat {e}}_{i}} \right)\otimes \mathbf {{\hat {e}}_{i}} ,$$где $\otimes$ является внешним оператором продукта .

Кроме того, если a само выражается как векторное произведение: $$\mathbf {a} =\mathbf {c} \times \mathbf {d}$$затем $$[\mathbf {a} ]_{\times }=\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }.$$

Доказательство подстановкой

Оценка векторного произведения дает $$\mathbf {a} =\mathbf {c} \times \mathbf {d} ={\begin{pmatrix}c_{2}d_{3}-c_{3}d_{2}\\c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}\end{pmatrix}}$$Следовательно, левая часть равна $$[\mathbf {a} ]_{\times }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}$$Теперь, что касается правой стороны, $$\mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{1}d_{2}&c_{1}d_{3}\\c_{2}d_{1}&c_{2}d_{2}&c_{2}d_{3}\\c_{3}d_{1}&c_{3}d_{2}&c_{3}d_{3}\end{bmatrix}}$$И его транспонирование $$\mathbf {d} \mathbf {c} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{2}d_{1}&c_{3}d_{1}\\c_{1}d_{2}&c_{2}d_{2}&c_{3}d_{2}\\c_{1}d_{3}&c_{2}d_{3}&c_{3}d_{3}\end{bmatrix}}$$Оценка правой части дает $$\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}$$Сравнение показывает, что левая часть равна правой.

Этот результат можно обобщить на более высокие измерения с помощью геометрической алгебры . В частности, бивекторы любого измерения могут быть идентифицированы с кососимметричными матрицами, поэтому произведение кососимметричной матрицы и вектора эквивалентно части 1-го класса произведения бивектора и вектора. В трех измерениях бивекторы двойственны векторам, поэтому произведение эквивалентно векторному произведению, причем бивектор вместо вектора, двойственного ему. В более высоких измерениях произведение все еще можно вычислить, но бивекторы имеют больше степеней свободы и не эквивалентны векторам.

С этими обозначениями зачастую гораздо проще работать, например, в эпиполярной геометрии .

Из общих свойств векторного произведения сразу следует, что $$[\mathbf {a} ]_{\times }\,\mathbf {a} =\mathbf {0}$$ и $$\mathbf {a} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }=\mathbf {0}$$а из того, что [ a ] _​​× кососимметрично, следует, что $$\mathbf {b} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }\,\mathbf {b} =0.$$

Упомянутое выше тройное разложение произведения (правило Бака-Каба) можно легко доказать, используя эти обозначения.

Как упоминалось выше, алгебра Ли R ³ с векторным произведением изоморфна алгебре Ли so(3) , элементы которой можно отождествить с кососимметричными матрицами 3×3. Отображение a → [ a ] _​​× обеспечивает изоморфизм между R ³ и так(3) . При этом отображении векторное произведение 3-векторов соответствует коммутатору кососимметричных матриц размером 3х3.

showПреобразование матрицы для векторного произведения с каноническими базовыми векторами

Denoting with $\mathbf {e} _{i}\in \mathbf {R} ^{3\times 1}$ the $i$-th canonical base vector, the cross product of a generic vector $\mathbf {v} \in \mathbf {R} ^{3\times 1}$ with $\mathbf {e} _{i}$ is given by: $\mathbf {v} \times \mathbf {e} _{i}=\mathbf {C} _{i}\mathbf {v}$, where $$\mathbf {C} _{1}={\begin{bmatrix}0&0&0\\0&0&1\\0&-1&0\end{bmatrix}},\quad \mathbf {C} _{2}={\begin{bmatrix}0&0&-1\\0&0&0\\1&0&0\end{bmatrix}},\quad \mathbf {C} _{3}={\begin{bmatrix}0&1&0\\-1&0&0\\0&0&0\end{bmatrix}}$$ These matrices share the following properties: $\mathbf {C} _{i}^{\textrm {T}}=-\mathbf {C} _{i}$ (skew-symmetric); Both trace and determinant are zero; ${\text{rank}}(\mathbf {C} _{i})=2$; $\mathbf {C} _{i}\mathbf {C} _{i}^{\textrm {T}}=\mathbf {P} _{\mathbf {e} _{i}}^{^{\perp }}$ (see below); The orthogonal projection matrix of a vector $\mathbf {v} \neq \mathbf {0}$ is given by $\mathbf {P} _{\mathbf {v} }=\mathbf {v} \left(\mathbf {v} ^{\textrm {T}}\mathbf {v} \right)^{-1}\mathbf {v} ^{T}$. The projection matrix onto the orthogonal complement is given by $\mathbf {P} _{\mathbf {v} }^{^{\perp }}=\mathbf {I} -\mathbf {P} _{\mathbf {v} }$, where $\mathbf {I}$ is the identity matrix. For the special case of $\mathbf {v} =\mathbf {e} _{i}$, it can be verified that $$\mathbf {P} _{\mathbf {e} _{1}}^{^{\perp }}={\begin{bmatrix}0&0&0\\0&1&0\\0&0&1\end{bmatrix}},\quad \mathbf {P} _{\mathbf {e} _{2}}^{^{\perp }}={\begin{bmatrix}1&0&0\\0&0&0\\0&0&1\end{bmatrix}},\quad \mathbf {P} _{\mathbf {e} _{3}}^{^{\perp }}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}$$ For other properties of orthogonal projection matrices, see projection (linear algebra).

Обозначение индекса для тензоров

В качестве альтернативы векторное произведение можно определить через тензор Леви-Чивита E _ijk и скалярное произведение η. ^мне , которые полезны при преобразовании векторной записи для тензорных приложений:

$\mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\eta ^{mi}E_{ijk}a^{j}b^{k}$

где индексы $i,j,k$ соответствуют компонентам вектора. Эта характеристика векторного произведения часто выражается более компактно с использованием соглашения Эйнштейна о суммировании как

$\mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\eta ^{mi}E_{ijk}a^{j}b^{k}$

в котором повторяющиеся индексы суммируются по значениям от 1 до 3.

В положительно ориентированном ортонормированном базисе η ^мне = д ^мне ( дельта Кронекера ) и $E_{ijk}=\varepsilon _{ijk}$ ( символ Леви-Чивита ). В этом случае это представление является другой формой кососимметричного представления векторного произведения:

$[\varepsilon _{ijk}a^{j}]=[\mathbf {a} ]_{\times }.$

В классической механике : представление векторного произведения с помощью символа Леви-Чивита может привести к тому, что механическая симметрия станет очевидной, когда физические системы изотропны . (Пример: рассмотрим частицу в потенциале закона Гука в трехмерном пространстве, свободно колеблющуюся в трех измерениях; ни одно из этих измерений не является «особым» ни в каком смысле, поэтому симметрия заключается в угловом моменте, представленном перекрестным произведением, который поясняются вышеупомянутым изображением Леви-Чивита).

Мнемоника

Мнемоника для расчета векторного произведения в векторной форме

«Xyzzy (мнемоника)» перенаправляется сюда. Чтобы узнать о других значениях, см. Xyzzy .

Слово «xyzzy» можно использовать, чтобы запомнить определение векторного произведения.

Если

$\mathbf {a} =\mathbf {b} \times \mathbf {c}$

где:

$\mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}},\ \mathbf {b} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}},\ \mathbf {c} ={\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}$

затем:

$a_{x}=b_{y}c_{z}-b_{z}c_{y}$

$a_{y}=b_{z}c_{x}-b_{x}c_{z}$

$a_{z}=b_{x}c_{y}-b_{y}c_{x}.$

Второе и третье уравнения можно получить из первого, просто вращая индексы по вертикали: x → y → z → x . Проблема, конечно, в том, как запомнить первое уравнение, и для этого доступны два варианта: либо запомнить соответствующие две диагонали схемы Сарруса (содержащие i ), либо запомнить последовательность xyzzy.

Поскольку первая диагональ в схеме Сарруса — это всего лишь главная диагональ матрицы упомянутой выше 3×3, первые три буквы слова xyzzy можно запомнить очень легко.

Перекрестная визуализация

Подобно приведенному выше мнемоническому устройству, между двумя векторами в уравнении можно визуализировать «крест» или X. Это может быть полезно для запоминания правильной формулы перекрестного произведения.

Если

$\mathbf {a} =\mathbf {b} \times \mathbf {c}$

затем:

$\mathbf {a} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}.$

Если мы хотим получить формулу $a_{x}$ мы просто отбрасываем $b_{x}$ и $c_{x}$ из формулы и уберите следующие два компонента:

$a_{x}={\begin{bmatrix}b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{y}\\c_{z}\end{bmatrix}}.$

Когда делаешь это для $a_{y}$ следующие два элемента вниз должны «обертывать» матрицу так, чтобы после компонента z следовал компонент x. Для наглядности при выполнении этой операции для $a_{y}$, следующими двумя компонентами должны быть z и x (именно в этом порядке). В то время как для $a_{z}$ следующие две компоненты следует принять за x и y.

$a_{y}={\begin{bmatrix}b_{z}\\b_{x}\end{bmatrix}}\times {\begin{bmatrix}c_{z}\\c_{x}\end{bmatrix}},\ a_{z}={\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\end{bmatrix}}$

Для $a_{x}$ затем, если мы визуализируем оператор перекрестия как указывающий от элемента слева к элементу справа, мы можем взять первый элемент слева и просто умножить его на элемент, на который указывает перекрестие в правой матрице. Затем мы вычитаем следующий элемент слева, умноженный на элемент, на который здесь указывает крестик. Это приводит к тому, что наш $a_{x}$ формула –

$a_{x}=b_{y}c_{z}-b_{z}c_{y}.$

Мы можем сделать это таким же образом для $a_{y}$ и $a_{z}$ построить связанные с ними формулы.

Приложения

Перекрестное произведение имеет приложения в различных контекстах. Например, он используется в вычислительной геометрии, физике и технике.Ниже приводится неисчерпывающий список примеров.

Вычислительная геометрия

Взаимное произведение появляется при вычислении расстояния двух косых линий (линий, не находящихся в одной плоскости) друг от друга в трехмерном пространстве.

Векторное произведение можно использовать для вычисления нормали к треугольнику или многоугольнику — операция, часто выполняемая в компьютерной графике . Например, вращение многоугольника (по часовой стрелке или против часовой стрелки) вокруг точки внутри многоугольника можно вычислить путем триангуляции многоугольника (как у колеса со спицами) и суммирования углов (между спицами), используя векторное произведение для отслеживания знак каждого угла.

В вычислительной геометрии плоскости определяемого векторное произведение используется для определения знака острого угла, тремя точками. $p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})$ и $p_{3}=(x_{3},y_{3})$. Это соответствует направлению (вверх или вниз) векторного произведения двух компланарных векторов, определяемых двумя парами точек. $(p_{1},p_{2})$ и $(p_{1},p_{3})$. Знак острого угла является знаком выражения

$P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),$

что представляет собой длину знака векторного произведения двух векторов.

В «правой» системе координат, если результат равен 0, точки лежат на одной прямой ; если он положителен, три точки составляют положительный угол поворота вокруг $p_{1}$ от $p_{2}$ к $p_{3}$, в противном случае отрицательный угол. С другой точки зрения, признак $P$ говорит ли $p_{3}$ лежит слева или справа от линии $p_{1},p_{2}.$

Перекрестное произведение используется при вычислении объема многогранника, такого как тетраэдр или параллелепипед .

Угловой момент и крутящий момент

Угловой момент L частицы относительно заданного начала координат определяется как:

$\mathbf {L} =\mathbf {r} \times \mathbf {p} ,$

где r — вектор положения частицы относительно начала координат, p — линейный импульс частицы.

Точно так же момент M силы F _B, приложенной в точке B вокруг точки A, определяется как:

$\mathbf {M} _{\mathrm {A} }=\mathbf {r} _{\mathrm {AB} }\times \mathbf {F} _{\mathrm {B} }\,$

В механике момент силы также называют крутящим моментом и записывают как $\mathbf {\tau }$

Поскольку положение r , линейный момент p и сила F являются истинными векторами, как угловой момент L , так и момент силы M являются псевдовекторами или аксиальными векторами .

Твердое тело

Перекрестное произведение часто появляется при описании жестких движений. Две точки P и Q на твердом теле могут быть связаны соотношением:

$\mathbf {v} _{P}-\mathbf {v} _{Q}={\boldsymbol {\omega }}\times \left(\mathbf {r} _{P}-\mathbf {r} _{Q}\right)\,$

где $\mathbf {r}$ это положение точки, $\mathbf {v}$ это его скорость и ${\boldsymbol {\omega }}$ тела — угловая скорость .

Поскольку позиция $\mathbf {r}$ и скорость $\mathbf {v}$ — истинные векторы, угловая скорость ${\boldsymbol {\omega }}$ — псевдовектор или аксиальный вектор .

сила Лоренца

Смотрите также: сила Лоренца

Векторное произведение используется для описания силы Лоренца, действующей на движущийся электрический заряд q _e :

$\mathbf {F} =q_{e}\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$

Поскольку скорость v , сила F и электрическое поле E являются истинными векторами, магнитное поле B является псевдовектором .

Другой

В векторном исчислении векторное произведение используется для определения формулы векторного оператора ротора .

Трюк с переписыванием векторного произведения в терминах матричного умножения часто встречается в эпиполярной и многовидовой геометрии, в частности, при выводе ограничений соответствия.

В качестве внешнего продукта

Перекрестное произведение по отношению к внешнему произведению. Красным показаны ортогональный единичный вектор и «параллельный» единичный бивектор.

Перекрестное произведение можно определить через внешнее произведение. Его можно обобщить на внешний продукт не только в трех измерениях. Это обобщение позволяет получить естественную геометрическую интерпретацию векторного произведения. Во внешней алгебре внешнее произведение двух векторов является бивектором. Бивектор — это ориентированный плоский элемент, почти так же, как вектор — это ориентированный линейный элемент. Учитывая два вектора a и b , можно рассматривать бивектор a ∧ b как ориентированный параллелограмм, натянутый на a и b . Затем векторное произведение получается путем взятия звезды Ходжа бивектора a ∧ b и отображения 2-векторов в векторы:

$a\times b=\star (a\wedge b).$

Это можно рассматривать как ориентированный многомерный элемент, «перпендикулярный» бивектору. В d -мерном пространстве звезда Ходжа преобразует k -вектор в ( d–k )-вектор; таким образом, только в измерениях d = 3 результатом является элемент размерности один (3–2 = 1), т.е. вектор. Например, в измерениях d = 4 векторное произведение двух векторов имеет размерность 4–2 = 2, что дает бивектор. Таким образом, только в трех измерениях векторное произведение определяет структуру алгебры для умножения векторов.

Рукава

Последовательность

Когда законы физики записаны в виде уравнений, можно сделать произвольный выбор системы координат, включая ориентацию. Следует быть осторожным и никогда не записывать уравнение, в котором обе стороны не ведут себя одинаково при всех преобразованиях, которые необходимо учитывать. Например, если одна часть уравнения представляет собой векторное произведение двух полярных векторов , нужно учитывать, что результатом является аксиальный вектор . Следовательно, для согласованности другая сторона также должна быть осевым вектором. В более общем смысле, результатом векторного произведения может быть либо полярный вектор, либо аксиальный вектор, в зависимости от типа его операндов (полярные векторы или аксиальные векторы). А именно, полярные векторы и аксиальные векторы при применении векторного произведения взаимосвязаны следующим образом:

• полярный вектор × полярный вектор = аксиальный вектор
• осевой вектор × осевой вектор = осевой вектор
• полярный вектор × аксиальный вектор = полярный вектор
• аксиальный вектор × полярный вектор = полярный вектор

или символически

• полярный × полярный = осевой
• осевой × осевой = осевой
• полярный × осевой = полярный
• осевой × полярный = полярный

Поскольку векторное произведение также может быть полярным вектором, оно не может изменить направление при преобразовании зеркального отображения. Это происходит в соответствии с приведенными выше соотношениями, если один из операндов является полярным вектором, а другой — аксиальным вектором (например, векторным произведением двух полярных векторов). Например, векторное тройное произведение, включающее три полярных вектора, является полярным вектором.

Подход без ручности возможен с использованием внешней алгебры.

Парадокс ортонормированного базиса

Пусть ( i , j , k ) — ортонормированный базис. Векторы i , j и k не зависят от ориентации пространства. Их можно определить даже при отсутствии какой-либо ориентации. Поэтому они не могут быть аксиальными векторами. Но если i и j — полярные векторы, то k — аксиальный вектор для i × j = k или j × i = k . Это парадокс.

«Осевой» и «полярный» являются физическими определителями физических векторов; то есть векторы, которые представляют физические величины, такие как скорость или магнитное поле. Векторы i , j и k являются математическими векторами, не аксиальными и не полярными. В математике векторное произведение двух векторов является вектором. Противоречия нет.

Обобщения

Существует несколько способов обобщить векторное произведение на более высокие измерения.

Алгебра Ли

Основная статья: Алгебра Ли

Взаимное произведение можно рассматривать как одно из простейших произведений Ли, и, таким образом, оно обобщается алгебрами Ли , которые аксиоматизируются как бинарные произведения, удовлетворяющие аксиомам полилинейности, кососимметрии и тождеству Якоби. Существует множество алгебр Ли, и их изучение является основной областью математики, называемой теорией Ли .

Например, алгебра Гейзенберга дает другую структуру алгебры Ли на $\mathbf {R} ^{3}.$ В основе $\{x,y,z\},$ продукт $[x,y]=z,[x,z]=[y,z]=0.$

Кватернионы

Дополнительная информация: кватернионы и пространственное вращение.

Перекрестное произведение также можно описать с помощью кватернионов .В общем, если вектор [ a ₁ , a ₂ , a ₃ ] представлен как кватернион a ₁ i + a ₂ j + a ₃ k , векторное произведение двух векторов можно получить, взяв их произведение как кватернионы и удалив реальная часть результата. Действительная часть будет отрицательным скалярным произведением двух векторов.

Октонионы

См. Также: Семимерное векторное произведение и Октонион.

Перекрестное произведение для 7-мерных векторов можно получить таким же образом, используя октонионы вместо кватернионов. Отсутствие нетривиальных векторных произведений двух векторов в других измерениях связано с результатом теоремы Гурвица о том, что единственными нормированными алгебрами с делением являются алгебры размерности 1, 2, 4 и 8.

Экстерьер продукта

Основные статьи: Внешняя алгебра и Сравнение векторной алгебры и геометрической алгебры § Перекрестные и внешние произведения

В общей размерности не существует прямого аналога двоичного векторного произведения, которое дает именно вектор. Однако существует внешний продукт, который имеет аналогичные свойства, за исключением того, что внешний продукт двух векторов теперь является 2-вектором , а не обычным вектором. Как упоминалось выше, векторное произведение можно интерпретировать как внешнее произведение в трех измерениях, используя оператор звезды Ходжа для отображения 2-векторов в векторы. Двойственный Ходжу внешний продукт дает ( n - 2) -вектор, который является естественным обобщением векторного произведения в любом количестве измерений.

Внешний продукт и скалярное произведение можно объединить (посредством суммирования) для формирования геометрического произведения в геометрической алгебре.

Внешний продукт

Как упоминалось выше, векторное произведение можно интерпретировать в трех измерениях как двойственное Ходжа внешнему произведению. В любых конечных n измерениях двойственное по Ходжу внешнее произведение n - 1 векторов является вектором. Таким образом, вместо бинарной операции в произвольных конечных измерениях векторное произведение обобщается как двойственное по Ходжу внешнее произведение некоторых заданных n - 1 векторов. Это обобщение называется внешним продуктом .

Коммутаторный продукт

Основные статьи: Геометрическая алгебра § Расширения внутренних и внешних произведений , Взаимное произведение § Взаимное произведение и направленность и Взаимное произведение § Алгебра Ли.

Интерпретируя трехмерное векторное пространство алгебры как 2-векторную (а не 1-векторную) подалгебру трехмерной геометрической алгебры, где $\mathbf {i} =\mathbf {e_{2}} \mathbf {e_{3}}$, $\mathbf {j} =\mathbf {e_{1}} \mathbf {e_{3}}$, и $\mathbf {k} =\mathbf {e_{1}} \mathbf {e_{2}}$векторное произведение точно соответствует коммутаторному произведению в геометрической алгебре, и оба используют один и тот же символ $\times$. Коммутаторное произведение определено для 2-векторов $A$ и $B$ в геометрической алгебре как:

$A\times B={\tfrac {1}{2}}(AB-BA),$

где $AB$ является геометрическим произведением.

Коммутаторное произведение можно обобщить на произвольные мультивекторы в трех измерениях, в результате чего мультивектор будет состоять только из элементов классов 1 (1-векторы/ истинные векторы ) и 2 (2-векторы/псевдовекторы). Хотя коммутаторное произведение двух 1-векторов действительно совпадает с внешним произведением и дает 2-вектор, коммутатор 1-вектора и 2-вектора дает истинный вектор, соответствующий вместо этого левому и правому сжатию в геометрическая алгебра. Коммутаторное произведение двух 2-векторов не имеет соответствующего эквивалентного произведения, поэтому коммутаторное произведение определяется в первую очередь для 2-векторов. Более того, тройное произведение коммутаторов трех 2-векторов совпадает с векторным тройным произведением тех же трех псевдовекторов в векторной алгебре. Однако тройное произведение коммутатора трех 1-векторов в геометрической алгебре вместо этого является отрицательным векторным тройным произведением тех же трех истинных векторов в векторной алгебре.

Обобщения на более высокие измерения обеспечиваются тем же коммутаторным произведением 2-векторов в многомерных геометрических алгебрах, но 2-вектора больше не являются псевдовекторами. Точно так же, как коммутаторное произведение/перекрестное произведение 2-векторов в трех измерениях соответствует простейшей алгебре Ли , 2-векторные подалгебры геометрической алгебры более высокой размерности, оснащенные коммутаторным произведением, также соответствуют алгебрам Ли. Как и в трех измерениях, произведение коммутатора можно далее обобщить на произвольные мультивекторы.

Полилинейная алгебра

В контексте полилинейной алгебры векторное произведение можно рассматривать как (1,2)-тензор ( смешанный тензор , в частности билинейное отображение ), полученный из трехмерной формы объема , (0,3)-тензор, повышая индекс .

В деталях трехмерная объемная форма определяет продукт. $V\times V\times V\to \mathbf {R} ,$ взяв определитель матрицы, заданной этими тремя векторами. По двойственности это эквивалентно функции $V\times V\to V^{*},$ (фиксация любых двух входов дает функцию $V\to \mathbf {R}$ путем оценки на третьем входе) и при наличии внутреннего продукта (например, скалярного произведения; в более общем смысле, невырожденной билинейной формы) мы имеем изоморфизм $V\to V^{*},$ и, таким образом, это дает карту $V\times V\to V,$ которое является векторным произведением: (0,3)-тензор (3 векторных входа, скалярный выход) был преобразован в (1,2)-тензор (2 векторных входа, 1 векторный выход) путем «повышения индекса».

Переводя приведенную выше алгебру в геометрию, функция «объем параллелепипеда, определяемого формулой $(a,b,-)$" (где первые два вектора фиксированы, а последний является входными), что определяет функцию $V\to \mathbf {R}$, можно однозначно представить как скалярное произведение с вектором: этот вектор является векторным произведением $a\times b.$ С этой точки зрения векторное произведение определяется скалярным тройным произведением $\mathrm {Vol} (a,b,c)=(a\times b)\cdot c.$

Точно так же в более высоких измерениях можно определить обобщенные векторные произведения, повышая индексы n -мерной формы объема, которая представляет собой $(0,n)$-тензор.Наиболее прямые обобщения векторного произведения заключаются в определении:

• а $(1,n-1)$-тензор, который принимает в качестве входных данных $n-1$ векторов и выдает на выходе 1 вектор – $(n-1)$-арное векторное произведение, или
• а $(n-2,2)$-тензор, который принимает на вход 2 вектора и выдает на выходе кососимметричный тензор ранга n - 2 – двоичное произведение со значениями тензора ранга n - 2 . Можно также определить $(k,n-k)$-тензоры для других k .

Все эти произведения являются полилинейными и кососимметричными и могут быть определены в терминах определителя и четности .

The $(n-1)$-арный продукт можно описать следующим образом: задано $n-1$ векторы $v_{1},\dots ,v_{n-1}$ в $\mathbf {R} ^{n},$ определить их обобщенное векторное произведение $v_{n}=v_{1}\times \cdots \times v_{n-1}$ как:

• перпендикулярно гиперплоскости, определяемой $v_{i},$
• Величина - это объем параллелоэдра, определяемый $v_{i},$ который можно вычислить как определитель Грама $v_{i},$
• ориентирован так, что $v_{1},\dots ,v_{n}$ позитивно ориентирован.

Это уникальный многолинейный переменный продукт, который оценивается как $e_{1}\times \cdots \times e_{n-1}=e_{n}$, $e_{2}\times \cdots \times e_{n}=e_{1},$ и так далее для циклических перестановок индексов.

В координатах можно дать формулу для этого $(n-1)$-арный аналог векторного произведения в R ^н к:

$\bigwedge _{i=0}^{n-1}\mathbf {v} _{i}={\begin{vmatrix}v_{1}{}^{1}&\cdots &v_{1}{}^{n}\\\vdots &\ddots &\vdots \\v_{n-1}{}^{1}&\cdots &v_{n-1}{}^{n}\\\mathbf {e} _{1}&\cdots &\mathbf {e} _{n}\end{vmatrix}}.$

Эта формула по структуре идентична формуле определителя для нормального векторного произведения в R ³ за исключением того, что строка базисных векторов является последней строкой определителя, а не первой. Причина этого заключается в том, чтобы гарантировать, что упорядоченные векторы ( v ₁ , ..., v _{n −1} , Λ ^{п –1}
_i=0 v _i ) имеют положительную ориентацию относительно ( e ₁ , ..., en ₎ . Если n нечетное, эта модификация оставляет значение неизменным, поэтому это соглашение согласуется с обычным определением двоичного произведения. Однако в случае, когда n четное, различие должно быть сохранено. Этот $(n-1)$-арная форма обладает многими из тех же свойств, что и векторное векторное произведение: она переменная и линейная по своим аргументам, она перпендикулярна каждому аргументу, а ее величина дает гиперобъем области, ограниченной аргументами. И так же, как векторное векторное произведение, его можно определить независимым от координат способом как двойственное по Ходжу клиновое произведение аргументов. Более того, продукт $[v_{1},\ldots ,v_{n}]:=\bigwedge _{i=0}^{n}v_{i}$ удовлетворяет тождеству Филиппова,

$[[x_{1},\ldots ,x_{n}],y_{2},\ldots ,y_{n}]]=\sum _{i=1}^{n}[x_{1},\ldots ,x_{i-1},[x_{i},y_{2},\ldots ,y_{n}],x_{i+1},\ldots ,x_{n}],$

и поэтому он наделяет R ^п+1 со структурой n-алгебры Ли (см. предложение 1 ).

История

В 1773 году Жозеф-Луи Лагранж использовал компонентную форму скалярного и векторного произведений для изучения тетраэдра в трех измерениях.

В 1843 году Уильям Роуэн Гамильтон ввел произведение кватернионов , а вместе с ним и термины вектор и скаляр . Учитывая два кватерниона [0, u ] и [0, v ] , где u и v — векторы в R ³ , их кватернионное произведение можно суммировать как [− u ⋅ v , u × v ] . Джеймс Клерк Максвелл использовал кватернионные инструменты Гамильтона для разработки своих знаменитых уравнений электромагнетизма , и по этой и другим причинам кватернионы какое-то время были важной частью физического образования.

В 1844 году Герман Грассман опубликовал геометрическую алгебру, не привязанную к размерности два или три. Грассманн разработал несколько продуктов, в том числе векторное произведение, обозначаемое тогда [uv] . ( См. также: внешняя алгебра . )

В 1853 году Огюстен-Луи Коши , современник Грассмана, опубликовал статью об алгебраических ключах, которые использовались для решения уравнений и имели те же свойства умножения, что и векторное произведение.

В 1878 году Уильям Кингдон Клиффорд опубликовал «Элементы динамики» термин «векторное произведение» , в которых засвидетельствован . В книге это произведение двух векторов определяется как имеющее величину, равную площади параллелограмма , двумя сторонами которого они являются, и направление, перпендикулярное их плоскости. ( См. также: Алгебра Клиффорда . )

В конспектах лекций 1881 года Гиббс представил векторное произведение как $u\times v$ и назвал это косым произведением . В 1901 году ученик Гибба Эдвин Бидуэлл Уилсон отредактировал и расширил эти конспекты лекций в учебник «Векторный анализ» . Уилсон сохранил термин «косое произведение» , но заметил, что альтернативные термины «перекрестное произведение» и векторное произведение встречались чаще.

В 1908 году Чезаре Бурали-Форти и Роберто Марколонго ввели обозначение векторного произведения u ∧ v . Он используется во Франции и других регионах до сих пор, как символ $\times$ уже используется для обозначения умножения и декартова произведения .

См. также

• Декартово произведение – произведение двух множеств.
• Геометрическая алгебра: вращающиеся системы
• Множественные перекрестные произведения - продукты, включающие более трех векторов.
• Умножение векторов
• Четверной продукт
• × (символ)

Библиография

• Каджори, Флориан (1929). История математических обозначений, том II . Издательство «Открытый суд» . п. 134 . ISBN  978-0-486-67766-8 .
• Кроу, Майкл Дж. (1994). История векторного анализа . Дувр. ISBN  0-486-67910-1 .
• Э. А. Милн (1948) Векторная механика , Глава 2: Векторное произведение, стр. 11–31, Лондон: Methuen Publishing .
• Уилсон, Эдвин Бидвелл (1901). Векторный анализ: учебник для студентов-математиков и физиков, основанный на лекциях Дж. Уилларда Гиббса . Издательство Йельского университета .
• Т. Леви-Чивита; У. Амальди (1949). Уроки рациональной механики (на итальянском языке). Болонья: издательство Zanichelli.

Внешние ссылки

• «Векторное произведение» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Быстрый геометрический вывод и интерпретация векторных произведений
• Интерактивное руководство, созданное в Сиракузском университете – (требуется Java )
• В. Кахан (2007). Перекрестные произведения и вращения в евклидовом 2- и 3-мерном пространстве. Калифорнийский университет в Беркли (PDF).
• Векторное произведение , Mathcentre (Великобритания), 2009 г.