Векторные обозначения

Векторные обозначения

Векторная стрелка
Указывая от А к Б

Векторные компоненты
Описание вектора стрелки v его координатами x и y дает изоморфизм векторных пространств.

Скалярное произведение
Две последовательности координатных векторов одинаковой длины и возвращают одно число.

Векторный продукт
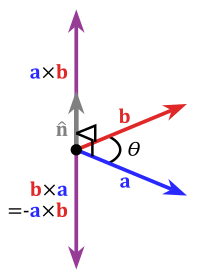
Перекрестное произведение относительно правой системы координат

В математике и физике является векторная запись широко используемой записью для представления векторов . которые могут быть евклидовыми векторами или, в более общем смысле, членами векторного пространства .

Для представления вектора общепринятым типографским соглашением является строчный и прямой жирный шрифт, как в v . Международная организация по стандартизации (ISO) рекомендует либо жирный курсив с засечками, как в v , либо нежирный курсив с засечками, подчеркнутый стрелкой вправо, как в ${\vec {v}}$.

В высшей математике векторы часто обозначаются простым курсивом, как и любая переменная .

История

В 1835 году Джусто Беллавитис представил идею равнонаправленных отрезков прямой. $AB\bumpeq CD$ что привело к понятию вектора как класса эквивалентности таких отрезков.

Термин «вектор» был придуман У. Р. Гамильтоном примерно в 1843 году, когда он открыл кватернионы — систему, которая использует векторы и скаляры для охвата четырехмерного пространства. Для кватерниона q = a + b i + c j + d k Гамильтон использовал две проекции: S q = a для скалярной части q и V q = b i + c j + d k для векторной части. Используя современные термины перекрестное произведение (×) и скалярное произведение (.), кватернионное произведение двух векторов p и q можно записать pq = – p . д + п × д . В 1878 году У. К. Клиффорд разделил эти два произведения, чтобы сделать операцию кватерниона полезной для студентов в своем учебнике « Элементы динамики» . Читая лекции в Йельском университете , Джозайя Уиллард Гиббс предложил обозначения для скалярного произведения и векторного произведения , которые были введены в векторном анализе .

В 1891 году Оливер Хевисайд убеждал Кларендона отличать векторы от скаляров. критиковал использование греческих букв Тейтом и готических букв Максвеллом Он .

В 1912 году Дж. Б. Шоу опубликовал свою «Сравнительную запись векторных выражений» в Бюллетене Общества кватернионов . Впоследствии Александр Макфарлейн описал в той же публикации 15 критериев четкой экспрессии с помощью векторов.

Векторные идеи были выдвинуты Германом Грассманом в 1841 году и снова в 1862 году на немецком языке . Но немецких математиков кватернионы интересовали не так сильно, как англоговорящих математиков. Когда Феликс Кляйн организовывал немецкую математическую энциклопедию , он поручил Арнольду Зоммерфельду стандартизировать векторную запись. В 1950 году, когда издательство Academic Press опубликовало перевод Г. Куэрти второго издания второго тома « Лекций по теоретической физике» Зоммерфельда, векторные обозначения были предметом сноски: «В оригинальном немецком тексте векторы и их компоненты напечатаны в для этого перевода был принят более обычный способ типографского различия между ними».

Прямоугольные координаты

Прямоугольник

Прямоугольный кубоид

См. также: Реальное координатное пространство.

Учитывая декартову систему координат , вектор может быть определен его декартовыми координатами .

Обозначение кортежа

Вектор v в n -мерном реальном координатном пространстве можно задать с помощью кортежа (упорядоченного списка) координат:

$\mathbf {v} =(v_{1},v_{2},\dots ,v_{n-1},v_{n})$

Иногда угловые скобки $\langle \dots \rangle$ используются вместо круглых скобок.

Матричное обозначение

Вектор в $\mathbb {R} ^{n}$ строк или столбцов, также может быть указан как матрица содержащая упорядоченный набор компонентов. Вектор, заданный как матрица-строка, известен как вектор-строка ; тот, который указан как матрица-столбец, известен как вектор-столбец .

И снова n -мерный вектор $\mathbf {v}$ может быть задан в любой из следующих форм с использованием матриц:

• $\mathbf {v} ={\begin{bmatrix}v_{1}&v_{2}&\cdots &v_{n-1}&v_{n}\end{bmatrix}}={\begin{pmatrix}v_{1}&v_{2}&\cdots &v_{n-1}&v_{n}\end{pmatrix}}$
• $\mathbf {v} ={\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n-1}\\v_{n}\end{bmatrix}}={\begin{pmatrix}v_{1}\\v_{2}\\\vdots \\v_{n-1}\\v_{n}\end{pmatrix}}$

где v ₁ , v ₂ , …, v _{n - 1} , v _n — компоненты v . В некоторых расширенных контекстах строка и вектор-столбец имеют разное значение; см . ковариацию и контравариантность векторов подробнее .

Обозначение единичного вектора

Вектор в $\mathbb {R} ^{3}$ (или меньшее количество измерений, например $\mathbb {R} ^{2}$ где v _z ниже равно нулю) можно определить как сумму скалярных кратных компонентов вектора с членами стандартного базиса в $\mathbb {R} ^{3}$. Базис представлен единичными векторами ${\boldsymbol {\hat {\imath }}}=(1,0,0)$, ${\boldsymbol {\hat {\jmath }}}=(0,1,0)$, и ${\boldsymbol {\hat {k}}}=(0,0,1)$.

Трехмерный вектор ${\boldsymbol {v}}$ может быть задан в следующей форме, используя обозначение единичного вектора:

$$\mathbf {v} =v_{x}{\boldsymbol {\hat {\imath }}}+v_{y}{\boldsymbol {\hat {\jmath }}}+v_{z}{\boldsymbol {\hat {k}}}$$

где v _x , v _y и v _z скалярные компоненты v . Скалярные компоненты могут быть положительными или отрицательными; абсолютное значение скалярной компоненты - это ее величина.

Полярные координаты

Точки в полярной системе координат с полюсом и полярной осью L. O Зеленым цветом обозначена точка с радиальной координатой 3 и угловой координатой 60 градусов или (3,60°). Синим цветом обозначена точка (4210°).

Две полярные координаты точки на плоскости можно рассматривать как двумерный вектор. Такой вектор состоит из величины (или длины) и направления (или угла). Величина, обычно обозначаемая как r , представляет собой расстояние от начальной точки, начала координат , до изображаемой точки. Угол, обычно обозначаемый как θ ( греческая буква тета ), представляет собой угол, обычно измеряемый против часовой стрелки, между фиксированным направлением, обычно направлением положительной оси X , и направлением от начала координат до точки. Угол обычно уменьшают, чтобы он находился в пределах диапазона $0\leq \theta <2\pi$ радианы или $0\leq \theta <360^{\circ }$.

Обозначения упорядоченного множества и матриц

Векторы могут быть заданы либо с использованием нотации упорядоченных пар (подмножество нотации упорядоченного множества, использующей только два компонента), либо с использованием матричной нотации, как в случае с прямоугольными координатами. В этих формах первым компонентом вектора является r (вместо v ₁ ), а вторым компонентом является θ (вместо v ₂ ). Чтобы отличить полярные координаты от прямоугольных координат, перед углом может стоять символ угла: $\angle$.

Двумерные полярные координаты для v могут быть представлены как любое из следующего, используя обозначение упорядоченной пары или матрицы:

• $\mathbf {v} =(r,\angle \theta )$
• $\mathbf {v} =\langle r,\angle \theta \rangle$
• $\mathbf {v} ={\begin{bmatrix}r&\angle \theta \end{bmatrix}}$
• $\mathbf {v} ={\begin{bmatrix}r\\\angle \theta \end{bmatrix}}$

где r - величина, θ - угол, а символ угла ( $\angle$) является необязательным.

Прямая запись

Векторы также можно задать с помощью упрощенных автономных уравнений, которые явно определяют r и θ . Это может быть громоздко, но полезно, чтобы избежать путаницы с двумерными прямоугольными векторами, возникающей из-за использования обозначений упорядоченных пар или матриц.

Двумерный вектор, величина которого равна 5 единицам и направление которого составляет π /9 радиан (20°), можно задать в любой из следующих форм:

• $r=5,\ \theta ={\pi \over 9}$
• $r=5,\ \theta =20^{\circ }$

Цилиндрические векторы

Цилиндрическая система координат с началом , полярной осью A и продольной осью L. O Точка — точка с радиальным расстоянием ρ = 4, угловой координатой φ = 130° и высотой z = 4.

Цилиндрический вектор — это расширение концепции полярных координат на три измерения. Это похоже на стрелку в цилиндрической системе координат . Цилиндрический вектор задается расстоянием в плоскости xy , углом и расстоянием от плоскости xy (высотой). Первое расстояние, обычно обозначаемое как r или ρ (греческая буква ро ), представляет собой величину проекции вектора на плоскость xy . Угол, обычно обозначаемый как θ или φ (греческая буква фи ), измеряется как смещение от линии, коллинеарной оси x , в положительном направлении; угол обычно уменьшается, чтобы находиться в пределах диапазона $0\leq \theta <2\pi$. Второе расстояние, обычно обозначаемое как h или z , — это расстояние от плоскости xy до конечной точки вектора.

Обозначения упорядоченного множества и матриц

Цилиндрические векторы используют полярные координаты, где второй компонент расстояния объединяется с третьим компонентом для формирования упорядоченных троек (опять же, подмножества обозначений упорядоченного множества) и матриц. Перед углом может стоять символ угла ( $\angle$); Комбинация расстояние-угол-расстояние отличает цилиндрические векторы в этих обозначениях от сферических векторов в аналогичных обозначениях.

Трехмерный цилиндрический вектор v может быть представлен как любой из следующих, используя упорядоченный тройной или матричный обозначение:

• $\mathbf {v} =(r,\angle \theta ,h)$
• $\mathbf {v} =\langle r,\angle \theta ,h\rangle$
• $\mathbf {v} ={\begin{bmatrix}r&\angle \theta &h\end{bmatrix}}$
• $\mathbf {v} ={\begin{bmatrix}r\\\angle \theta \\h\end{bmatrix}}$

Где r — величина проекции v на плоскость xy , θ — угол между положительной осью x и v , а h — высота от плоскости xy до конечной точки v . Опять же, символ угла ( $\angle$) является необязательным.

Прямая запись

Цилиндрический вектор также можно задать напрямую, используя упрощенные автономные уравнения, которые определяют r (или ρ ), θ (или φ ) и h (или z ). При выборе имен переменных следует соблюдать единообразие; ρ не следует смешивать с θ и так далее.

Трехмерный вектор, величина проекции которого на плоскость xy равна 5 единицам, угол от положительной оси x равен π /9 радиан (20°), а высота от плоскости xy равна 3 единицам, может указываться в любой из следующих форм:

• $r=5,\ \theta ={\pi \over 9},\ h=3$
• $r=5,\ \theta =20^{\circ },\ h=3$
• $\rho =5,\ \phi ={\pi \over 9},\ z=3$
• $\rho =5,\ \phi =20^{\circ },\ z=3$

Сферические векторы

Сферические координаты ( r , θ , φ ), часто используемые в математике : радиальное расстояние r , азимутальный угол θ и полярный угол φ . Значения θ и φ поменялись местами по сравнению с физическим соглашением.

Сферический вектор — это еще один метод расширения концепции полярных векторов на три измерения. Это похоже на стрелку в сферической системе координат . Сферический вектор задается величиной, азимутальным углом и зенитным углом. Величина обычно обозначается как ρ . Угол азимута, обычно обозначаемый как θ , представляет собой смещение (против часовой стрелки) от положительной оси x . Зенитный угол, обычно обозначаемый как φ , представляет собой смещение от положительной оси z . Оба угла обычно уменьшаются до значения в диапазоне от нуля (включительно) до 2 π (не включая).

Обозначения упорядоченного множества и матриц

Сферические векторы задаются как полярные векторы, где зенитный угол объединяется как третий компонент для формирования упорядоченных троек и матриц. Перед углами азимута и зенита может стоять символ угла ( $\angle$); префикс следует использовать последовательно для создания комбинации расстояние-угол-угол, которая отличает сферические векторы от цилиндрических.

Трехмерный сферический вектор v может быть представлен как любой из следующих, используя либо упорядоченный триплет, либо матричную запись:

• $\mathbf {v} =(\rho ,\angle \theta ,\angle \phi )$
• $\mathbf {v} =\langle \rho ,\angle \theta ,\angle \phi \rangle$
• $\mathbf {v} ={\begin{bmatrix}\rho &\angle \theta &\angle \phi \end{bmatrix}}$
• $\mathbf {v} ={\begin{bmatrix}\rho \\\angle \theta \\\angle \phi \end{bmatrix}}$

Где ρ — магнитуда, θ — угол азимута, а φ — зенитный угол.

Прямая запись

Подобно полярным и цилиндрическим векторам, сферические векторы можно задать с помощью упрощенных автономных уравнений, в данном случае для ρ , θ и φ .

Трехмерный вектор, величина которого равна 5 единицам, азимутальный угол которого равен π /9 радиан (20°) и зенитный угол которого равен π /4 радиан (45°), можно задать как:

• $\rho =5,\ \theta ={\pi \over 9},\ \phi ={\pi \over 4}$
• $\rho =5,\ \theta =20^{\circ },\ \phi =45^{\circ }$

Операции

В любом заданном векторном пространстве определены операции сложения векторов и скалярного умножения. Нормированные векторные пространства также определяют операцию, известную как норма (или определение величины). Пространства внутреннего продукта также определяют операцию, известную как внутренний продукт. В $\mathbb {R} ^{n}$внутренний продукт известен как скалярное произведение . В $\mathbb {R} ^{3}$ и $\mathbb {R} ^{7}$ дополнительная операция, известная как векторное произведение , также определена .

Сложение векторов

Сложение векторов обозначается знаком плюс, используемым в качестве оператора между двумя векторами. Сумма двух векторов u и v будет представлена ​​как:

$$\mathbf {u} +\mathbf {v}$$

Скалярное умножение

Скалярное умножение представляется так же, как и алгебраическое умножение. Скаляр рядом с вектором (любой из них или оба могут быть в круглых скобках) подразумевает скалярное умножение. Два обычных оператора, точка и повернутый крест, также приемлемы (хотя повернутый крест почти никогда не используется), но они рискуют запутаться со скалярными произведениями и векторными произведениями, которые работают с двумя векторами. Произведение скаляра k на вектор v можно представить любым из следующих способов:

• $k\mathbf {v}$
• $k\cdot \mathbf {v}$

векторов и

Используя алгебраические свойства вычитания и деления, а также скалярное умножение, также можно «вычесть» два вектора и «делить» вектор на скаляр.

Вычитание вектора выполняется путем добавления скаляра, кратного -1, со вторым векторным операндом к первому векторному операнду. Это можно представить с помощью знака минус в качестве оператора. Разницу между двумя векторами u и v можно представить одним из следующих способов:

• $\mathbf {u} +-\mathbf {v}$
• $\mathbf {u} -\mathbf {v}$

Скалярное деление выполняется путем умножения векторного операнда на число, обратное скалярному операнду. Это можно представить с помощью дроби или знаков деления в качестве операторов. Частное вектора v и скаляра c может быть представлено в любой из следующих форм:

• ${1 \over c}\mathbf {v}$
• ${\mathbf {v} \over c}$
• ${\mathbf {v} \div c}$

Норма

Норма . вектора обозначается двойными чертами по обе стороны от вектора Норму вектора v можно представить как:

$$\|\mathbf {v} \|$$

Норму также иногда обозначают отдельными полосками, например $|\mathbf {v} |$, но это можно спутать с абсолютным значением (который является разновидностью нормы).

Внутренний продукт

Внутреннее произведение двух векторов (также известное как скалярное произведение, не путать со скалярным умножением) представляется в виде упорядоченной пары, заключенной в угловые скобки. Внутренний продукт двух векторов u и v будет представлен как:

$$\langle \mathbf {u} ,\mathbf {v} \rangle$$

Скалярное произведение

В $\mathbb {R} ^{n}$внутренний продукт также известен как скалярное произведение . В дополнение к стандартной нотации внутреннего произведения также может использоваться (и более распространено) нотация скалярного произведения (с использованием точки в качестве оператора). Скалярное произведение двух векторов u и v можно представить как:

$$\mathbf {u} \cdot \mathbf {v}$$

В некоторых старых источниках скалярное произведение подразумевается между двумя векторами, написанными рядом. Это обозначение можно спутать с диадным произведением двух векторов.

Перекрестное произведение

Перекрестное произведение двух векторов (в $\mathbb {R} ^{3}$) представлено с использованием повернутого креста в качестве оператора. Перекрестное произведение двух векторов u и v будет представлено как:

$$\mathbf {u} \times \mathbf {v}$$

По некоторым соглашениям (например, во Франции и в некоторых областях высшей математики) это также обозначается клином, что позволяет избежать путаницы с произведением-клином , поскольку они функционально эквивалентны в трех измерениях:

$$\mathbf {u} \wedge \mathbf {v}$$

используются следующие обозначения В некоторой более старой литературе для векторного произведения между u и v :

$$[\mathbf {u} ,\mathbf {v} ]$$

Набла

Основные статьи: символ Дель и Набла

Векторные обозначения используются в исчислении через оператор Набла :

$$\mathbf {i} {\frac {\partial }{\partial x}}+\mathbf {j} {\frac {\partial }{\partial y}}+\mathbf {k} {\frac {\partial }{\partial z}}$$

скалярной функции f градиент При использовании записывается как $\nabla f\,,$

с векторным полем дивергенция записывается F как $\nabla \cdot F,$

а с векторным полем F ротор записывается как $\nabla \times F.$

См. также

• Евклидов вектор
• ISO 31-11 § Векторы и тензоры
• Фазор