Матрица ДПФ

В прикладной математике матрица ДПФ представляет собой выражение дискретного преобразования Фурье (ДПФ) в виде матрицы преобразования , которую можно применить к сигналу посредством умножения матриц .

Определение

-точечное ДПФ N выражается как умножение $X=Wx$, где $x$ исходный входной сигнал, $W$ представляет собой N матрицу ДПФ размером на N квадратную , и $X$ – ДПФ сигнала.

Матрица преобразования $W$ может быть определен как $W=\left({\frac {\omega ^{jk}}{\sqrt {N}}}\right)_{j,k=0,\ldots ,N-1}$или эквивалентно:

$W={\frac {1}{\sqrt {N}}}{\begin{bmatrix}1&1&1&1&\cdots &1\\1&\omega &\omega ^{2}&\omega ^{3}&\cdots &\omega ^{N-1}\\1&\omega ^{2}&\omega ^{4}&\omega ^{6}&\cdots &\omega ^{2(N-1)}\\1&\omega ^{3}&\omega ^{6}&\omega ^{9}&\cdots &\omega ^{3(N-1)}\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\1&\omega ^{N-1}&\omega ^{2(N-1)}&\omega ^{3(N-1)}&\cdots &\omega ^{(N-1)(N-1)}\end{bmatrix}}$,

где $\omega =e^{-2\pi i/N}$ является примитивным корнем N-й степени из единицы , в котором $i^{2}=-1$. Мы можем избежать записи больших показателей для $\omega$ используя тот факт, что для любого показателя $x$ у нас есть личность $\omega ^{x}=\omega ^{x{\bmod {N}}}.$ Это матрица Вандермонда для корней из единицы с точностью до нормировочного множителя. Обратите внимание, что нормировочный коэффициент перед суммой ( $1/{\sqrt {N}}$ ) и знак показателя степени в ω являются просто соглашениями и различаются в некоторых трактовках. Все последующее обсуждение применимо независимо от соглашения, с минимальными изменениями. Единственное, что важно, это то, что прямое и обратное преобразования имеют показатели степени противоположного знака и чтобы произведение их коэффициентов нормализации было 1/ N . Однако $1/{\sqrt {N}}$ Выбор здесь делает результирующую матрицу ДПФ унитарной , что удобно во многих случаях.

Алгоритмы быстрого преобразования Фурье используют симметрию матрицы, чтобы сократить время умножения вектора на эту матрицу по сравнению с обычным $O(N^{2})$. Аналогичные методы можно применять для умножения на такие матрицы, как матрица Адамара и матрица Уолша .

Примеры

Двухточечный

Двухточечное ДПФ — это простой случай, в котором первая запись — это DC (сумма), а вторая запись — AC (разница).

$W={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}$

Первая строка выполняет сумму, а вторая строка — разность.

Фактор $1/{\sqrt {2}}$ заключается в том, чтобы сделать преобразование унитарным (см. ниже).

Четырехточечный

Четырехточечная матрица ДПФ по часовой стрелке выглядит следующим образом:

$W={\frac {1}{\sqrt {4}}}{\begin{bmatrix}\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}\\\omega ^{0}&\omega ^{1}&\omega ^{2}&\omega ^{3}\\\omega ^{0}&\omega ^{2}&\omega ^{4}&\omega ^{6}\\\omega ^{0}&\omega ^{3}&\omega ^{6}&\omega ^{9}\\\end{bmatrix}}={\frac {1}{\sqrt {4}}}{\begin{bmatrix}1&1&1&1\\1&-i&-1&i\\1&-1&1&-1\\1&i&-1&-i\end{bmatrix}}$

где $\omega =e^{-{\frac {2\pi i}{4}}}=-i$.

Восьмиточечный

Первая нетривиальная целая степень двойки относится к восьми точкам:

$W={\frac {1}{\sqrt {8}}}{\begin{bmatrix}\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}\\\omega ^{0}&\omega ^{1}&\omega ^{2}&\omega ^{3}&\omega ^{4}&\omega ^{5}&\omega ^{6}&\omega ^{7}\\\omega ^{0}&\omega ^{2}&\omega ^{4}&\omega ^{6}&\omega ^{8}&\omega ^{10}&\omega ^{12}&\omega ^{14}\\\omega ^{0}&\omega ^{3}&\omega ^{6}&\omega ^{9}&\omega ^{12}&\omega ^{15}&\omega ^{18}&\omega ^{21}\\\omega ^{0}&\omega ^{4}&\omega ^{8}&\omega ^{12}&\omega ^{16}&\omega ^{20}&\omega ^{24}&\omega ^{28}\\\omega ^{0}&\omega ^{5}&\omega ^{10}&\omega ^{15}&\omega ^{20}&\omega ^{25}&\omega ^{30}&\omega ^{35}\\\omega ^{0}&\omega ^{6}&\omega ^{12}&\omega ^{18}&\omega ^{24}&\omega ^{30}&\omega ^{36}&\omega ^{42}\\\omega ^{0}&\omega ^{7}&\omega ^{14}&\omega ^{21}&\omega ^{28}&\omega ^{35}&\omega ^{42}&\omega ^{49}\\\end{bmatrix}}={\frac {1}{\sqrt {8}}}{\begin{bmatrix}1&1&1&1&1&1&1&1\\1&\omega &-i&-i\omega &-1&-\omega &i&i\omega \\1&-i&-1&i&1&-i&-1&i\\1&-i\omega &i&\omega &-1&i\omega &-i&-\omega \\1&-1&1&-1&1&-1&1&-1\\1&-\omega &-i&i\omega &-1&\omega &i&-i\omega \\1&i&-1&-i&1&i&-1&-i\\1&i\omega &i&-\omega &-1&-i\omega &-i&\omega \\\end{bmatrix}}$

где

$\omega =e^{-{\frac {2\pi i}{8}}}={\frac {1}{\sqrt {2}}}-{\frac {i}{\sqrt {2}}}$

(Обратите внимание, что $\omega ^{8+n}=\omega ^{n}$.)

Оценка стоимости $\omega$, дает:

$W={\frac {1}{\sqrt {8}}}{\begin{bmatrix}1&1&1&1&1&1&1&1\\1&{\frac {1-i}{\sqrt {2}}}&-i&{\frac {-1-i}{\sqrt {2}}}&-1&{\frac {-1+i}{\sqrt {2}}}&i&{\frac {1+i}{\sqrt {2}}}\\1&-i&-1&i&1&-i&-1&i\\1&{\frac {-1-i}{\sqrt {2}}}&i&{\frac {1-i}{\sqrt {2}}}&-1&{\frac {1+i}{\sqrt {2}}}&-i&{\frac {-1+i}{\sqrt {2}}}\\1&-1&1&-1&1&-1&1&-1\\1&{\frac {-1+i}{\sqrt {2}}}&-i&{\frac {1+i}{\sqrt {2}}}&-1&{\frac {1-i}{\sqrt {2}}}&i&{\frac {-1-i}{\sqrt {2}}}\\1&i&-1&-i&1&i&-1&-i\\1&{\frac {1+i}{\sqrt {2}}}&i&{\frac {-1+i}{\sqrt {2}}}&-1&{\frac {-1-i}{\sqrt {2}}}&-i&{\frac {1-i}{\sqrt {2}}}\\\end{bmatrix}}$

На следующем изображении ДПФ изображено как умножение матрицы, при этом элементы матрицы изображены выборками комплексных экспонент:

Действительная часть (косинусоида) обозначена сплошной линией, а мнимая часть (синусоида) — пунктирной линией.

В верхнем ряду представлены все единицы (в масштабе $1/{\sqrt {8}}$ для унитарности), поэтому он «измеряет» постоянную составляющую входного сигнала. Следующая строка представляет собой восемь отсчетов отрицательного одного цикла комплексной экспоненты, т. е. сигнала с дробной частотой -1/8, поэтому он «измеряет», сколько «силы» имеется на дробной частоте +1/8 в сигнал. Напомним, что согласованный фильтр сравнивает сигнал с обращенной во времени версией того, что мы ищем, поэтому, когда мы ищем fracfreq. 1/8 сравниваем с fracfreq. −1/8, поэтому эта строка имеет отрицательную частоту . Следующая строка представляет собой отрицательные два цикла комплексной экспоненты, выбранные в восьми местах, поэтому она имеет дробную частоту -1/4 и, таким образом, «измеряет» степень, в которой сигнал имеет дробную частоту +1/4.

Ниже кратко описывается, как работает 8-точечное ДПФ, строка за строкой, с точки зрения дробной частоты:

• 0 измеряет величину постоянного тока в сигнале
• −1/8 показывает, какая часть сигнала имеет дробную частоту +1/8.
• −1/4 показывает, какая часть сигнала имеет дробную частоту +1/4.
• −3/8 показывает, какая часть сигнала имеет дробную частоту +3/8.
• −1/2 показывает, какая часть сигнала имеет дробную частоту +1/2.
• −5/8 измеряет, какая часть сигнала имеет дробную частоту +5/8.
• −3/4 измеряет, какая часть сигнала имеет дробную частоту +3/4.
• −7/8 измеряет, какая часть сигнала имеет дробную частоту +7/8.

Эквивалентно можно сказать, что последняя строка имеет дробную частоту +1/8 и, таким образом, измеряет, какая часть сигнала имеет дробную частоту -1/8. Таким образом, можно сказать, что верхние строки матрицы «измеряют» положительную частотную составляющую сигнала, а нижние строки измеряют отрицательную частотную составляющую сигнала.

Унитарное преобразование

ДПФ является (или может быть, благодаря соответствующему выбору масштабирования) унитарным преобразованием, т. е. преобразованием, сохраняющим энергию. Подходящим выбором масштабирования для достижения унитарности является $1/{\sqrt {N}}$, так что энергия в физической области будет такой же, как энергия в области Фурье, т. е. для удовлетворения теоремы Парсеваля . (Для удобства вычислений также обычно используются другие, неунитарные масштабирования; например, теорема о свертке принимает немного более простую форму с масштабированием, показанным в статье о дискретном преобразовании Фурье .)

Другие объекты недвижимости

Другие свойства матрицы ДПФ, включая ее собственные значения, связь со свертками, приложения и т. д., см. в статье о дискретном преобразовании Фурье .

Предельный случай: оператор Фурье

Основная статья: оператор Фурье

Действительная часть (косинус)

Мнимая часть (синус)

Оператор Фурье

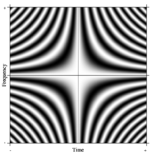
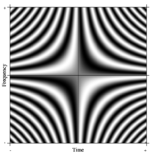
Понятие преобразования Фурье легко обобщается . Одно из таких формальных обобщений N -точечного ДПФ можно представить, взяв N сколь угодно большим. В пределе строгий математический аппарат рассматривает такие линейные операторы как так называемые интегральные преобразования . В этом случае, если мы создадим очень большую матрицу с комплексными экспонентами в строках (т. е. косинус действительными частями и синус мнимыми частями) и неограниченно увеличим разрешение, мы приблизимся к ядру интегрального уравнения Фредгольма 2-го рода: а именно оператор Фурье , который определяет непрерывное преобразование Фурье. Прямоугольная часть этого непрерывного оператора Фурье может отображаться как изображение, аналогичное матрице ДПФ, как показано справа, где значение пикселя в оттенках серого обозначает числовую величину.

См. также

• Многомерное преобразование
• Матрицы часов и сдвигов
• Теорема Чеботарева о корнях из единицы

Ссылки

• Справочник по преобразованию и сжатию данных ПК Йип, К. Рамамохан Рао - см. главу 2, где рассматривается ДПФ, основанное в основном на матрице ДПФ.

Внешние ссылки

• Оператор Фурье и децимация во времени (DIT)