Матрица расстояний
Эта статья нуждается в дополнительных цитатах для проверки . ( февраль 2017 г. ) |
В математике , информатике и особенно в теории графов матрица расстояний — это квадратная матрица (двумерный массив), содержащая попарно взятые расстояния между элементами множества. [1] В зависимости от используемого приложения расстояние , используемое для определения этой матрицы, может быть или не быть метрикой . Если элементов N эта матрица будет иметь размер N × N. , В приложениях теории графов элементы чаще называют точками, узлами или вершинами.
Неметрическая матрица расстояний [ править ]
В общем случае матрица расстояний — это взвешенная матрица смежности некоторого графа. В сети , ориентированном графе с весами, присвоенными дугам, расстояние между двумя узлами сети можно определить как минимум сумм весов на кратчайших путях, соединяющих два узла. [2] Эта функция расстояния, хотя и четко определена, не является метрикой. Не должно быть никаких ограничений на веса, кроме необходимости комбинировать и сравнивать их, поэтому в некоторых приложениях используются отрицательные веса. Поскольку пути направлены, симметрия не может быть гарантирована, и если циклы существуют, матрица расстояний не может быть полой .
Алгебраическая формулировка вышесказанного может быть получена с помощью алгебры мин-плюс . Умножение матриц в этой системе определяется следующим образом: для двух n × n матриц размера A = ( a ij ) и B = ( b ij ) их произведение расстояний C = ( c ij ) = A ⭑ B определяется как n × n матрица такая, что
Обратите внимание, что недиагональные элементы, которые не соединены напрямую, должны быть установлены на бесконечность или подходящее большое значение, чтобы операции мин-плюс работали правильно. Ноль в этих местах будет неправильно интерпретирован как ребро без расстояния, стоимости и т. д.
Если W — матрица размера n × n , содержащая веса ребер графа , то W к (с использованием этого произведения расстояний) дает расстояния между вершинами с использованием путей длиной не более k ребер, а W н - матрица расстояний графа.
Произвольный граф G на n вершинах можно смоделировать как взвешенный полный граф на n вершинах, присвоив вес, равный единице, каждому ребру полного графа, соответствующему ребру G , и нулю всем остальным ребрам. W для этого полного графа является смежности G матрицей . Матрица расстояний G может быть вычислена из W , как указано выше, однако W н вычисляемый обычным матричным умножением, кодирует только количество путей между любыми двумя вершинами длиной ровно n .
Матрица метрических расстояний [ править ]
Ценность формализма матрицы расстояний во многих приложениях заключается в том, как матрица расстояний может явно кодировать метрические аксиомы и в том, как она пригодна для использования методов линейной алгебры. То есть, если M = ( x ij ) с 1 ≤ i , j ≤ N является матрицей расстояний для метрического расстояния, то
- все элементы на главной диагонали равны нулю (т. е. матрица представляет собой пустую матрицу ), т. е. x ii = 0 для всех 1 ≤ i ≤ N ,
- все недиагональные элементы положительны ( x ij > 0, если i ≠ j ), (то есть неотрицательная матрица ),
- матрица является симметричной матрицей ( x ij = x ji ), и
- для любых i и j ij x ( ≤ x ik + x kj для всех k неравенство треугольника). Это можно сформулировать с помощью умножения тропической матрицы.
Когда матрица расстояний удовлетворяет первым трем аксиомам (что делает ее полуметрикой), ее иногда называют матрицей предрасстояний. Матрица предрасстояний, которую можно встроить в евклидово пространство, называется евклидовой матрицей расстояний . Для данных смешанного типа, которые содержат как числовые, так и категориальные дескрипторы, расстояние Гауэра распространённой альтернативой является .
Другой распространенный пример метрической матрицы расстояний возникает в теории кодирования , когда в блочном коде элементы представляют собой строки фиксированной длины в алфавите, а расстояние между ними задается метрикой расстояния Хэмминга . Наименьшая ненулевая запись в матрице расстояний измеряет способность кода исправлять и обнаруживать ошибки.
расстояний Аддитивная матрица
Матрица аддитивных расстояний — это особый тип матрицы, используемый в биоинформатике для построения филогенетического дерева . Пусть x будет наименьшим общим предком между двумя видами i и j , мы ожидаем, что M ij = M ix + M xj . Вот откуда берется аддитивная метрика. Матрица расстояний M для набора видов S называется аддитивной тогда и только тогда, когда существует филогения T для S такая, что:
- Каждому ребру ( u , v ) в T сопоставлен положительный вес d uv
- Для каждого i , j ∈ S M ij от равен сумме весов на пути i до j в T
В этом случае M называется аддитивной матрицей, а T — аддитивным деревом. Ниже мы можем увидеть пример аддитивной матрицы расстояний и соответствующее ей дерево:

расстояний ультраметрических Матрица
Матрица ультраметрических расстояний определяется как аддитивная матрица, которая моделирует постоянные молекулярные часы . Используется для построения филогенетического дерева. Матрица M называется ультраметрической, если существует дерево T такое, что:
- M ij равен сумме весов ребер на пути от i до j в T
- Корень дерева можно определить, если расстояние до всех листьев одинаково.
Вот пример ультраметрической матрицы расстояний с соответствующим деревом:

Биоинформатика [ править ]
В этом разделе отсутствует информация о безцентровых мерах расстояний (Mash, K(r), FastANI, Skmer и т.д.); нужно меньше внимания к тому, как выполнять выравнивание (особенно с «тупым» DP), и больше внимания к тому, как получить расстояние от выравнивания. ( декабрь 2023 г. ) |
Матрица расстояний широко используется в области биоинформатики и присутствует в нескольких методах, алгоритмах и программах. Матрицы расстояний используются для представления белковых структур независимо от координат, а также попарных расстояний между двумя последовательностями в пространстве последовательностей . Они используются для структурного и последовательного выравнивания, а также для определения структур белков с помощью ЯМР или рентгеновской кристаллографии .
Иногда удобнее представлять данные в виде матрицы сходства .
Он также используется для определения корреляции расстояний .
Выравнивание последовательности [ править ]
Выравнивание двух последовательностей формируется путем вставки пробелов в произвольные места вдоль последовательностей так, чтобы они имели одинаковую длину и не было двух пробелов в одной и той же позиции двух дополненных последовательностей. [3] Одним из основных методов выравнивания последовательностей является динамическое программирование . Метод используется для заполнения матрицы расстояний и последующего получения выравнивания. Обычно для выравнивания последовательностей используется матрица для присвоения оценок совпадениям или несоответствиям аминокислот, а также штраф за пропуск за совпадение аминокислоты в одной последовательности с пробелом в другой.
Глобальное выравнивание [ править ]
Алгоритм Нидлмана-Вунша, используемый для расчета глобального выравнивания, использует динамическое программирование для получения матрицы расстояний.
Локальное выравнивание [ править ]
Алгоритм Смита-Уотермана также основан на динамическом программировании, которое также заключается в получении матрицы расстояний и последующем локальном выравнивании.
последовательностей Множественное выравнивание
Множественное выравнивание последовательностей — это расширение парного выравнивания, позволяющее выравнивать несколько последовательностей одновременно. Различные методы MSA основаны на той же идее матрицы расстояний, что и глобальные и локальные выравнивания.
- Метод центральной звезды. Этот метод определяет центральную последовательность Sc , которая минимизирует расстояние между последовательностью и Sc любой другой последовательностью S i . множественное выравнивание M для набора последовательностей S так, что для каждого выравнивания расстояние d M ( Sc , Si Si ) является Затем он генерирует оптимальным парным выравниванием. Особенностью этого метода является то, что вычисляется выравнивание для S , сумма парных расстояний которого не более чем в два раза превышает оптимальное множественное выравнивание.
- Метод прогрессивного выравнивания. Этот эвристический метод создания MSA сначала выравнивает две наиболее связанные последовательности, а затем постепенно выравнивает следующие две наиболее связанные последовательности, пока все последовательности не будут выровнены.
Есть и другие методы, которые имеют свою программу из-за своей популярности:
МАФФТ [ править ]
Множественное выравнивание с использованием быстрого преобразования Фурье (MAFFT) — это программа с алгоритмом, основанным на прогрессивном выравнивании, и предлагающая различные стратегии множественного выравнивания. Во-первых, MAFFT строит матрицу расстояний на основе количества общих шестикортежей. Во-вторых, он строит направляющее дерево на основе предыдущей матрицы. В-третьих, он кластеризует последовательности с помощью быстрого преобразования Фурье и запускает выравнивание. На основе нового выравнивания он реконструирует направляющее дерево и снова выравнивает.
Филогенетический анализ [ править ]
Этот раздел может потребовать очистки Википедии , чтобы соответствовать стандартам качества . Конкретная проблема заключается в следующем: следует урезать и по большей части упаковать в основную статью. Вот как работает WP:SPINOFF , верно? ( декабрь 2023 г. ) |
Чтобы выполнить филогенетический анализ, первым шагом является реконструкция филогенетического дерева: учитывая коллекцию видов, проблема состоит в том, чтобы реконструировать или сделать вывод о наследственных отношениях между видами, т. е. филогенетическом дереве между видами. Эту деятельность выполняют методы матрицы расстояний.
матрицы расстояний Методы
Методы филогенетического анализа с матрицей расстояний явно полагаются на меру «генетического расстояния» между классифицируемыми последовательностями и, следовательно, требуют нескольких последовательностей в качестве входных данных. Методы расстояния пытаются построить матрицу «все ко всем» из набора запросов последовательностей, описывающую расстояние между каждой парой последовательностей. На основе этого строится филогенетическое дерево, которое помещает близкородственные последовательности в один и тот же внутренний узел и длина ветвей которого точно воспроизводит наблюдаемые расстояния между последовательностями. Методы матрицы расстояний могут создавать как корневые, так и некорневые деревья, в зависимости от алгоритма, используемого для их расчета. [4] Для заданных n видов входными данными является размера n × n матрица расстояний M , где M ij — расстояние мутации между видами i и j . Цель состоит в том, чтобы вывести дерево степени 3 , соответствующее матрице расстояний.
Они часто используются в качестве основы для прогрессивных и итеративных типов множественного выравнивания последовательностей . Основным недостатком методов матрицы расстояний является их неспособность эффективно использовать информацию о локальных регионах с высокой изменчивостью, которые появляются в нескольких поддеревьях. [4] Несмотря на потенциальные проблемы, дистанционные методы чрезвычайно быстры и часто дают разумную оценку филогении. Они также имеют определенные преимущества перед методами, использующими символы напрямую. Примечательно, что дистанционные методы позволяют использовать данные, которые нелегко преобразовать в характерные данные, например, анализы гибридизации ДНК-ДНК .
Ниже приведены дистанционные методы реконструкции филогении:
- Аддитивная реконструкция дерева
- УПГМА
- Присоединение соседа
- Фитч-Марголиаш
дерева Аддитивная реконструкция
Реконструкция аддитивного дерева основана на аддитивных и ультраметрических матрицах расстояний. Эти матрицы имеют особую характеристику:
Рассмотрим аддитивную матрицу M . Для любых трех видов i, j, k соответствующее дерево уникально. [3] Каждая ультраметрическая матрица расстояний является аддитивной матрицей. Мы можем наблюдать это свойство для дерева ниже, которое состоит из видов i, j, k .

Техника реконструкции аддитивного дерева начинается с этого дерева. А затем каждый раз добавляет еще один вид на основе матрицы расстояний в сочетании с упомянутым выше свойством. Например, рассмотрим аддитивную матрицу M и 5 видов a , b , c , d и e . Сначала мы формируем аддитивное дерево для двух видов a и b . Затем мы выбрали третий, скажем, c , и прикрепили его к точке x на краю между a и b . Веса ребер вычисляются с использованием приведенного выше свойства. Далее мы добавляем четвертый вид d к любому из ребер. Если мы применим это свойство, то мы определим, что d должно быть прикреплено только к одному конкретному ребру. Наконец, мы добавляем e, следуя той же процедуре, что и раньше.
УПГМА [ править ]
Основной принцип UPGMA (метод невзвешенных парных групп со средним арифметическим) заключается в том, что похожие виды должны быть ближе на филогенетическом дереве. Следовательно, он строит дерево путем итеративной кластеризации подобных последовательностей. Метод работает путем построения филогенетического дерева снизу вверх из его листьев. Изначально у нас есть n листьев (или n которых представляет вид в S. одноэлементных деревьев), каждый из Эти n листьев называются n кластерами. Затем мы выполняем n -1 итераций. На каждой итерации мы идентифицируем два кластера C 1 и C 2 с наименьшим средним расстоянием и объединяем их, чтобы сформировать больший кластер C . Если мы предположим, что M является ультраметрическим, для любого кластера C , созданного алгоритмом UPGMA, C является допустимым ультраметрическим деревом.
Сосед присоединился [ править ]
Соседний метод кластеризации снизу вверх. Требуется матрица расстояний, определяющая расстояние между каждой парой последовательностей. Алгоритм начинается с полностью неразрешенного дерева, топология которого соответствует топологии звездообразной сети , и повторяет следующие шаги до тех пор, пока дерево не будет полностью разрешено и не станут известны длины всех ветвей:
- На основе текущей матрицы расстояний рассчитайте матрицу (определенную ниже).
- Найдите пару различных таксонов i и j (т. е. с), для которых значение наименьшее. Эти таксоны объединяются во вновь созданный узел, который связан с центральным узлом.
- Рассчитайте расстояние от каждого таксона пары до этого нового узла.
- Рассчитайте расстояние от каждого таксона вне этой пары до нового узла.
- Запустите алгоритм еще раз, заменив пару соединенных соседей новым узлом и используя расстояния, рассчитанные на предыдущем шаге. [5]
Фитч-Марголиаш [ править ]
Метод Фитча-Марголиаша использует взвешенный метод наименьших квадратов для кластеризации на основе генетического расстояния. Близкородственным последовательностям придается больший вес в процессе построения дерева, чтобы исправить повышенную неточность измерения расстояний между отдаленно родственными последовательностями. Критерий наименьших квадратов, применяемый к этим расстояниям, более точен, но менее эффективен, чем методы соединения соседей. Дополнительное улучшение, которое корректирует корреляции между расстояниями, возникающими из многих тесно связанных последовательностей в наборе данных, также может быть применено с увеличением вычислительных затрат. [6]
данных и машинное Интеллектуальный анализ обучение
Интеллектуальный анализ данных [ править ]
Распространенной функцией интеллектуального анализа данных является применение кластерного анализа к заданному набору данных для группировки данных на основе того, насколько они похожи или более похожи по сравнению с другими группами. Матрицы расстояний стали сильно зависимыми и использовались в кластерном анализе, поскольку сходство можно измерить с помощью метрики расстояния. Таким образом, матрица расстояний стала представлением меры сходства между всеми различными парами данных в наборе.
Иерархическая кластеризация [ править ]
Матрица расстояний необходима для традиционных алгоритмов иерархической кластеризации , которые часто представляют собой эвристические методы, используемые в биологических науках, таких как реконструкция филогении. При реализации любого из алгоритмов иерархической кластеризации при интеллектуальном анализе данных матрица расстояний будет содержать все попарные расстояния между каждой точкой, а затем начнет создавать кластеры между двумя разными точками или кластеры, полностью основанные на расстояниях из матрицы расстояний.
Если N — количество точек, сложность иерархической кластеризации равна:
- Временная сложность из-за повторяющихся вычислений, выполняемых после каждого кластера для обновления матрицы расстояний
- Пространственная сложность
Машинное обучение
Метрики расстояния являются ключевой частью нескольких алгоритмов машинного обучения, которые используются как в контролируемом , так и в неконтролируемом обучении . Обычно они используются для расчета сходства между точками данных: здесь важным элементом является матрица расстояний. Использование эффективной матрицы расстояний повышает производительность модели машинного обучения, будь то задачи классификации или кластеризации. [7]
K-Ближайшие соседи [ править ]
Матрица расстояний используется в алгоритме k-NN , который является одним из самых медленных, но простых и наиболее часто используемых алгоритмов машинного обучения на основе экземпляров, которые можно использовать как в задачах классификации, так и в задачах регрессии. Это один из самых медленных алгоритмов машинного обучения, поскольку для прогнозируемого результата каждой тестовой выборки требуется полностью вычисленная матрица расстояний между тестовой выборкой и каждой обучающей выборкой в обучающем наборе. После вычисления матрицы расстояний алгоритм выбирает количество K обучающих выборок, которые наиболее близки к тестовой выборке, чтобы спрогнозировать результат тестовой выборки на основе значения большинства (классификация) или среднего (регрессия) выбранного набора.
- Временная сложность прогнозирования , чтобы вычислить расстояние между каждой тестовой выборкой и каждой обучающей выборкой, чтобы построить матрицу расстояний, где:
- k = количество выбранных ближайших соседей
- n = размер обучающего набора
- d = количество измерений, используемых для данных
Эта модель, ориентированная на классификацию, прогнозирует метку цели на основе матрицы расстояний между целью и каждой из обучающих выборок, чтобы определить K-количество выборок, которые являются наиболее близкими/ближайшими к цели.
Компьютерное зрение [ править ]
Матрицу расстояний можно использовать в нейронных сетях для регрессии 2D в 3D в моделях машинного обучения для прогнозирования изображений.
Поиск информации [ править ]
смеси гауссовой расстояний с использованием расстояния Матрицы
- [1] * Расстояние гауссовой смеси для точного поиска ближайшего соседа для получения информации. В соответствии с установленной моделью гауссовской конечной смеси для распределения данных в базе данных расстояние гауссовой смеси формулируется на основе минимизации расхождения Кульбака-Лейблера между распределением извлекаемых данных и данными в базе данных. При сравнении характеристик расстояния гауссовой смеси с хорошо известными расстояниями Евклида и Махаланобиса , основанными на прецизионном измерении производительности, экспериментальные результаты показывают, что функция расстояния гауссовой смеси превосходит другие для различных типов тестовых данных.
Потенциальные базовые алгоритмы, на которые стоит обратить внимание по теме поиска информации, - это алгоритм поиска косяков рыб - поиск информации, который участвует в использовании матриц расстояний для сбора коллективного поведения косяков рыб. С помощью оператора кормления для обновления их веса
уравнение А:
уравнение Б:
Stepvol определяет размер максимального объемного смещения, предварительно сформированного с помощью матрицы расстояний, в частности, с использованием евклидовой матрицы расстояний .
Оценка сходства или несходства матриц косинусного сходства и расстояний [ править ]

- [2] * Хотя косинусная мера сходства , пожалуй, является наиболее часто применяемой мерой близости при поиске информации путем измерения углов между документами в пространстве поиска на основе косинуса. Евклидово расстояние инвариантно к средней поправке. Выборочное распределение среднего создается путем повторной выборки из одной и той же совокупности и записи полученных выборочных средних. Это формирует распределение различных средних значений, и это распределение имеет свое среднее значение и дисперсию. Для данных, которые могут быть как отрицательными, так и положительными, нулевое распределение косинусного сходства представляет собой распределение скалярного произведения двух независимых случайных единичных векторов. Это распределение имеет нулевое среднее значение и дисперсию 1/n. Тогда как евклидово расстояние будет инвариантным к этой поправке.
Кластеризация документов [ править ]
Реализация иерархической кластеризации с метриками на основе расстояния для организации и группировки схожих документов потребует необходимости и использования матрицы расстояний. Матрица расстояний будет представлять степень связи документа с другим документом, который будет использоваться для создания кластеров тесно связанных документов, которые будут использоваться в методах поиска соответствующих документов по запросу пользователя.
Изомап [ править ]
Isomap включает матрицы расстояний для использования геодезических расстояний для вычисления вложений меньшей размерности. Это помогает работать с коллекцией документов, находящихся в огромном количестве измерений, и позволяет выполнять кластеризацию документов.
Визуализатор поиска соседства (NeRV) [ править ]
Алгоритм, используемый как для неконтролируемой, так и для контролируемой визуализации, который использует матрицы расстояний для поиска похожих данных на основе сходства, показанного на дисплее/экране.
Матрица расстояний, необходимая для неконтролируемого NeRV, может быть вычислена с помощью фиксированных входных парных расстояний.
Матрица расстояний, необходимая для контролируемого NeRV, требует формулирования метрики контролируемого расстояния, чтобы иметь возможность вычислить расстояние до входа контролируемым образом.
Химия [ править ]
Матрица расстояний — математический объект, широко используемый как в графо-теоретическом (топологическом), так и в геометрическом (топографическом) вариантах химии. [8] Матрица расстояний используется в химии как в явной, так и в неявной форме.
между двумя Механизмы взаимопревращения пермутационными изомерами
Матрицы расстояний использовались в качестве основного подхода для изображения и выявления последовательности кратчайшего пути, необходимой для определения перегруппировки между двумя перестановочными изомерами.
и дистанционные Дистанционные спектры полиномы
Явное использование матриц расстояний требуется для построения полиномов расстояний и спектров расстояний молекулярных структур.
Модель структуры-свойства [ править ]
Неявное использование матриц расстояний было применено за счет использования основанной на расстоянии метрики числа Вайнера / индекса Вейнера , которая была сформулирована для представления расстояний во всех химических структурах. Число Вайнера равно полусумме элементов матрицы расстояний.
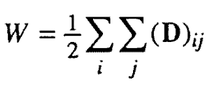
-графовая матрица Теоретико расстояний
Матрица расстояний в химии, которая используется для двумерной реализации молекулярных графов, которые используются для иллюстрации основных основополагающих особенностей молекулы во множестве приложений.
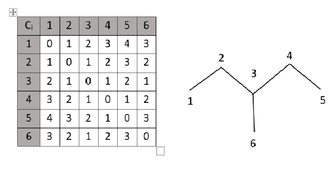
- Создание дерева меток, которое представляет углеродный скелет молекулы на основе ее матрицы расстояний. Матрица расстояний обязательна в этом приложении, потому что подобные молекулы могут иметь множество вариантов дерева меток своего углеродного скелета . Меченая древовидная структура углеродного скелета гексана (C 6 H 14 ), созданная на основе матрицы расстояний в примере, имеет различные варианты углеродного скелета, которые влияют как на матрицу расстояний, так и на меченое дерево.
- Создание помеченного графа с весами ребер, используемого в химической теории графов , который представляет молекулы с гетероатомами.
- Метод Леверье-Фадеева-Фрейма (LVFF) — компьютерно-ориентированный метод, используемый для ускорения процесса обнаружения центра графа в полициклических графах. Однако LVFF требует, чтобы входные данные представляли собой диагонализированную матрицу расстояний, которую легко решить путем реализации алгоритма трехдиагонального QL Хаусхолдера, который принимает матрицу расстояний и возвращает диагонализованное расстояние, необходимое для метода LVFF.
Матрица геометрических расстояний [ править ]
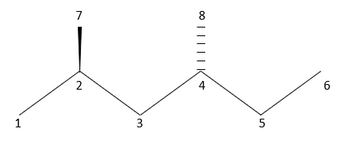
В то время как теоретико-графовая матрица расстояний 2-D отражает конституционные особенности молекулы, ее трехмерный (3D) характер закодирован в матрице геометрических расстояний. Матрица геометрических расстояний — это другой тип матрицы расстояний, основанный на матрице расстояний молекулы на основе теории графов для представления и построения графиков трехмерной структуры молекулы. [8] Матрица геометрических расстояний молекулярной структуры G представляет собой действительную симметричную матрицу размера n x n , определенную так же, как и двумерную матрицу. Однако матричные элементы D ij будут содержать набор кратчайших декартовых расстояний между i и j в G . Матрица геометрических расстояний, также известная как топографическая матрица, может быть построена на основе известной геометрии молекулы. матрица геометрических расстояний углеродного скелета 2,4-диметилгексана В качестве примера ниже представлена :
Другие приложения [ править ]
временных Анализ рядов
Матрицы расстояний динамического искажения времени используются с алгоритмами кластеризации и классификации коллекции/группы объектов временных рядов.
Примеры [ править ]
Например, предположим, что эти данные необходимо проанализировать, где пикселя евклидово расстояние — это метрика расстояния .

Матрица расстояний будет иметь вид:
| а | б | с | д | и | ж | |
|---|---|---|---|---|---|---|
| а | 0 | 184 | 222 | 177 | 216 | 231 |
| б | 184 | 0 | 45 | 123 | 128 | 200 |
| с | 222 | 45 | 0 | 129 | 121 | 203 |
| д | 177 | 123 | 129 | 0 | 46 | 83 |
| и | 216 | 128 | 121 | 46 | 0 | 83 |
| ж | 231 | 200 | 203 | 83 | 83 | 0 |
Эти данные затем можно просмотреть в графической форме в виде тепловой карты . На этом изображении черный цвет обозначает расстояние 0, а белый — максимальное расстояние.
См. также [ править ]
- Компьютерное зрение
- Кластеризация данных
- Установленное расстояние
- Полая матрица
- Умножение матрицы мин-плюс
Ссылки [ править ]
- ^ Вейенберг Г. и Йошида Р. (2015). Реконструкция филогении: Численные методы. В книге «Алгебраические и дискретно-математические методы современной биологии» (стр. 293–319). Академическая пресса.
- ^ Фрэнк Харари , Роберт З. Норман и Дорвин Картрайт (1965) Структурные модели: введение в теорию ориентированных графов , страницы 134–8, John Wiley & Sons MR 0184874
- ^ Jump up to: Перейти обратно: а б Сун, Винг-Кин (2010). Алгоритмы в биоинформатике: Практическое введение . Чепмен и Холл. п. 29. ISBN 978-1-4200-7033-0 .
- ^ Jump up to: Перейти обратно: а б Фельзенштейн, Джозеф (2003). Выводы о филогениях . Синауэр Ассошиэйтс. ISBN 9780878931774 .
- ^ Сайто, Наруя (1987). «Метод объединения соседей: новый метод реконструкции филогенетических деревьев» . Молекулярная биология и эволюция . 4 (4): 406–425. doi : 10.1093/oxfordjournals.molbev.a040454 . ПМИД 3447015 .
- ^ Фитч, Уолтер М. (1967). «Построение филогенетических деревьев: метод, основанный на расстояниях мутаций, оцененных по последовательностям цитохрома с, имеет общее применение» . Наука . 155 (3760): 279–284. дои : 10.1126/science.155.3760.279 . ПМИД 5334057 .
- ^ «4 типа дистанционных метрик в машинном обучении» . 25 февраля 2020 г.
- ^ Jump up to: Перейти обратно: а б Михалич, Златко (1992). «Матрица расстояний в химии». Журнал математической химии . 11 : 223–258. дои : 10.1007/BF01164206 . S2CID 121181446 .







