Динамическое искажение времени

Динамическое искажение времени между двумя кусочно-линейными функциями. Пунктирная линия иллюстрирует соотношение деформации времени. Обратите внимание, что несколько точек нижней функции сопоставляются с одной точкой верхней функции, и наоборот .

Два повторения последовательности ходьбы, записанные с помощью системы захвата движения. Несмотря на различия в скорости ходьбы между повторениями, пространственные траектории конечностей остаются очень похожими.

DTW между синусоидой и ее шумной и смещенной версией.

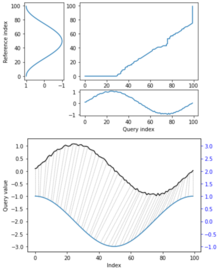
В временных рядов анализе динамическое искажение времени ( DTW ) — это алгоритм измерения сходства между двумя временными последовательностями, которые могут различаться по скорости. Например, сходство в ходьбе можно было обнаружить с помощью DTW, даже если один человек шел быстрее другого или если наблюдались ускорения в ходе наблюдения и замедления. DTW применяется к временным последовательностям видео, аудио и графических данных — действительно, любые данные, которые можно превратить в одномерную последовательность, можно проанализировать с помощью DTW. Хорошо известным применением является автоматическое распознавание речи , позволяющее справляться с различной скоростью речи. Другие приложения включают распознавание говорящего и распознавание подписей в Интернете . Его также можно использовать в приложениях для частичного сопоставления форм .

В общем, DTW — это метод, который вычисляет оптимальное соответствие между двумя заданными последовательностями (например, временными рядами ) с определенными ограничениями и правилами:

• Каждый индекс из первой последовательности должен соответствовать одному или нескольким индексам из другой последовательности, и наоборот.
• Первый индекс из первой последовательности должен совпадать с первым индексом из другой последовательности (но это не обязательно должно быть единственное совпадение).
• Последний индекс из первой последовательности должен совпадать с последним индексом из другой последовательности (но это не обязательно должно быть единственное совпадение).
• Отображение индексов первой последовательности в индексы другой последовательности должно быть монотонно возрастающим, и наоборот, т.е. если $j>i$ являются индексами из первой последовательности, то двух индексов быть не должно $l>k$ в другой последовательности, такой, что индекс $i$ соответствует индексу $l$ и индекс $j$ соответствует индексу $k$и наоборот

Мы можем построить каждое совпадение между последовательностями $1:M$ и $1:N$ как путь в $M\times N$ матрица из $(1,1)$ к $(M,N)$, такой, что каждый шаг является одним из $(0,1),(1,0),(1,1)$. В этой формулировке мы видим, что количество возможных совпадений — это число Деланной .

Оптимальное соответствие — это совпадение, которое удовлетворяет всем ограничениям и правилам и имеет минимальную стоимость, при этом стоимость вычисляется как сумма абсолютных разностей между их значениями для каждой сопоставленной пары индексов.

Последовательности нелинейно «искажаются» во временном измерении, чтобы определить степень их сходства независимо от определенных нелинейных изменений во временном измерении. Этот метод выравнивания последовательностей часто используется при классификации временных рядов. Хотя DTW измеряет величину, подобную расстоянию между двумя заданными последовательностями, он не гарантирует неравенства треугольника выполнение .

В дополнение к мере сходства между двумя последовательностями создается так называемый «путь деформации». Деформируя по этому пути, два сигнала можно выровнять во времени. Сигнал с исходным набором точек X (исходный), Y (исходный) преобразуется в X (искаженный), Y (искаженный). Это находит применение в генетической последовательности и синхронизации звука. С помощью этого метода можно усреднить последовательности с различной скоростью, см. раздел «Последовательность усреднения» .

Концептуально это очень похоже на алгоритм Нидлмана-Вунша .

Выполнение

Этот пример иллюстрирует реализацию алгоритма динамического преобразования времени, когда две последовательности s и t являются строками дискретных символов. Для двух символов x и y , d(x, y) расстояние между символами, например d(x, y) = $|x-y|$.

int DTWDistance(s: array [1..n], t: array [1..m]) {
    DTW := array [0..n, 0..m]
    
    for i := 0 to n
        for j := 0 to m
            DTW[i, j] := infinity
    DTW[0, 0] := 0
    
    for i := 1 to n
        for j := 1 to m
            cost := d(s[i], t[j])
            DTW[i, j] := cost + minimum(DTW[i-1, j  ],    // insertion
                                        DTW[i  , j-1],    // deletion
                                        DTW[i-1, j-1])    // match
    
    return DTW[n, m]
}

где DTW[i, j] это расстояние между s[1:i] и t[1:j] с лучшим выравниванием.

Иногда нам нужно добавить ограничение местоположения. То есть мы требуем, чтобы, если s[i] сопоставляется с t[j], затем $|i-j|$ не больше w , параметра окна.

Мы можем легко изменить приведенный выше алгоритм, добавив ограничение локальности (различия отмеченный ). Однако приведенная выше модификация работает только в том случае, если $|n-m|$ не больше w , т.е. конечная точка находится в пределах длины окна от диагонали. Чтобы алгоритм работал, параметр окна w должен быть адаптирован так, чтобы $|n-m|\leq w$ (см. строку, отмеченную (*) в коде).

int DTWDistance(s: array [1..n], t: array [1..m], w: int) {
    DTW := array [0..n, 0..m]

    w := max(w, abs(n-m)) // adapt window size (*)

    for i := 0 to n
        for j:= 0 to m
            DTW[i, j] := infinity
    DTW[0, 0] := 0
    for i := 1 to n
        for j := max(1, i-w) to min(m, i+w)
            DTW[i, j] := 0

    for i := 1 to n
        for j := max(1, i-w) to min(m, i+w)
            cost := d(s[i], t[j])
            DTW[i, j] := cost + minimum(DTW[i-1, j  ],    // insertion
                                        DTW[i  , j-1],    // deletion
                                        DTW[i-1, j-1])    // match
    return DTW[n, m]
}

Свойства деформации

Алгоритм DTW производит дискретное сопоставление существующих элементов одной серии с другой. Другими словами, он не позволяет масштабировать сегменты последовательности по времени. Другие методы допускают непрерывное деформирование. Например, Correlation Optimized Warping (COW) делит последовательность на однородные сегменты, которые масштабируются во времени с помощью линейной интерполяции, чтобы обеспечить наилучшее согласованное искажение. Масштабирование сегментов приводит к потенциальному созданию новых элементов путем масштабирования сегментов по времени в сторону уменьшения или увеличения и, таким образом, обеспечивает более чувствительную деформацию, чем дискретное сопоставление необработанных элементов в DTW.

Сложность

Временная сложность алгоритма DTW составляет $O(NM)$, где $N$ и $M$ — длины двух входных последовательностей. Квадратичный временной предел в 50 лет был нарушен в 2016 году: алгоритм Голда и Шарира позволяет вычислять DTW в $O({N^{2}}/\log \log N)$ время и пространство для двух входных последовательностей длины $N$. Этот алгоритм также можно адаптировать к последовательностям разной длины. Несмотря на это улучшение, было показано, что сильно субквадратичное время работы вида $O(N^{2-\epsilon })$ для некоторых $\epsilon >0$ не может существовать, если гипотеза сильного экспоненциального времени не подтвердится.

Хотя алгоритм динамического программирования для DTW требует $O(NM)$ пространства в простой реализации, потребление пространства может быть уменьшено до $O(\min(N,M))$ используя алгоритм Хиршберга .

Быстрое вычисление

Быстрые методы расчета DTW включают Early Abandoned и Pruned DTW, PrunedDTW, РазреженныйDTW, ФастДТВ, и MultiscaleDTW.

Распространенную задачу — получение аналогичных временных рядов — можно ускорить, используя нижние границы, такие как LB_Keogh, LB_Improved, LB_Улучшенный, LB_Уэбб или LB_Petitjean. Однако алгоритм Early Abandon и Pruned DTW снижает степень ускорения, обеспечиваемую нижней границей, а иногда делает его неэффективным.

В исследовании Wang et al. сообщили о немного лучших результатах с нижней границей LB_Improved, чем с границей LB_Keogh, и обнаружили, что другие методы были неэффективными. После этого исследования была разработана граница LB_Enhanced, которая всегда более точная, чем LB_Keogh, но при этом более эффективна для вычислений. LB_Petitjean — это самая точная известная нижняя граница, которую можно вычислить за линейное время.

Средняя последовательность

Усреднение динамического искажения времени — это проблема поиска средней последовательности для набора последовательностей. НЛААФ — это точный метод усреднения двух последовательностей с использованием DTW. Для более чем двух последовательностей проблема связана с множественным выравниванием и требует эвристики. администратор баз данных в настоящее время является эталонным методом для усреднения набора последовательностей в соответствии с DTW. КОМАСА эффективно рандомизирует поиск средней последовательности, используя DBA в качестве процесса локальной оптимизации.

Обучение под присмотром

Классификатор ближайшего соседа может достичь высочайшей производительности при использовании динамического искажения времени в качестве меры расстояния.

Амерсированное динамическое искажение времени

Amerced Dynamic Time Warping (ADTW) — это вариант DTW, предназначенный для лучшего контроля допустимости DTW в выравниваниях, которые он позволяет. Окна, которые классический DTW использует для ограничения выравнивания, представляют собой ступенчатую функцию. Любое искажение пути разрешено внутри окна и не за его пределами. Напротив, ADTW использует аддитивный штраф, который применяется каждый раз, когда путь искажается. Разрешено любое количество деформации, но каждое действие деформации влечет за собой прямой штраф. ADTW значительно превосходит DTW при использовании оконного режима при применении в качестве классификатора ближайшего соседа в наборе эталонных задач классификации временных рядов.

Графическое искажение времени

Графическое искажение времени (GTW) — это обобщенная версия DTW, которая может совместно выравнивать несколько пар временных рядов или последовательностей. По сравнению с независимым выравниванием нескольких пар с помощью DTW, GTW учитывает как точность выравнивания каждой пары последовательностей (как DTW), так и сходство между парами (в соответствии со структурой данных или назначенное пользователем). Это может привести к улучшению производительности выравнивания при наличии сходства между парами.

Функции расстояния

DTW чувствителен к функции расстояния $d(x,y)$ используется для оценки совпадений между парами значений в двух последовательностях. Исходное определение DTW использовал $d(x,y)=|x-y|$. В классификации временных рядов $d(x,y)=(x-y)^{2}$ стал популярным.

Недавняя работа показал, что настройка этой меры расстояния может быть полезна для настройки производительности DTW. В частности, настройка γ в семействе дистанционных функций вида $d(x,y)=|x-y|^{\gamma }$ заставляет DTW уделять больше внимания эффектам низкой амплитуды, когда γ мало, и эффектам большой амплитуды, когда γ велико.

Обработка пропущенных значений

DTW не может обрабатывать пропущенные значения во временных рядах. Простые методы предварительной обработки, такие как отбрасывание или интерполяция отсутствующих значений, не позволяют получить точную оценку расстояния DTW.

DTW-AROW (DTW с дополнительными ограничениями на деформацию) — это обобщение DTW для обработки пропущенных значений. DTW-AROW получает как расстояние, так и путь деформации; следовательно, его можно просто заменить на DTW для обработки пропущенных значений во многих приложениях. DTW-AROW имеет ту же сложность времени и памяти, что и DTW. Реализация DTW-AROW с открытым исходным кодом доступна на Python.

Альтернативные подходы

В функциональном анализе данных временные ряды рассматриваются как дискретизация гладких (дифференцируемых) функций времени. Рассматривая наблюдаемые выборки как гладкие функции, можно использовать непрерывную математику для анализа данных. Гладкость и монотонность функций деформации времени могут быть получены, например, путем интегрирования изменяющейся во времени радиальной базисной функции , что представляет собой одномерный диффеоморфизм . Оптимальные нелинейные функции деформации времени вычисляются путем минимизации меры расстояния набора функций до их искаженного среднего значения. Для функций деформации могут быть добавлены штрафные санкции за шероховатость, например, путем ограничения размера их кривизны. Полученные функции деформации являются плавными, что облегчает дальнейшую обработку. Этот подход успешно применяется для анализа закономерностей и изменчивости речевых движений.

Другой родственный подход - это скрытая модель Маркова (HMM), и было показано, что алгоритм Витерби, используемый для поиска наиболее вероятного пути через HMM, эквивалентен стохастическому DTW.

DTW и связанные с ним методы деформации обычно используются в качестве этапов предварительной или последующей обработки при анализе данных. Если обе наблюдаемые последовательности содержат случайные изменения в своих значениях, форме наблюдаемых последовательностей и случайном временном несовпадении, искажение может соответствовать шуму, что приведет к смещению результатов. Одновременная формулировка модели со случайным изменением как значений (по вертикали), так и временной параметризации (горизонтально) является примером нелинейной модели со смешанными эффектами . Было показано, что при анализе движений человека одновременное нелинейное моделирование смешанных эффектов дает превосходные результаты по сравнению с DTW.

Программное обеспечение с открытым исходным кодом

• Библиотека tempo C++ с привязками Python реализует Early Abandoned и Pruned DTW, а также Early Abandoned и Pruned ADTW и нижние границы DTW LB_Keogh, LB_Enhanced и LB_Webb.
• Библиотека UltraFastMPSearch Java реализует алгоритм UltraFastWWSearch. для быстрой настройки окон.
• Библиотека C++ lbimproved реализует алгоритмы быстрого поиска ближайших соседей под лицензией GNU General Public License (GPL). Он также обеспечивает реализацию динамического искажения времени на C++, а также различные нижние границы.
• Библиотека FastDTW — это реализация DTW на языке Java и реализация FastDTW, которая обеспечивает оптимальное или почти оптимальное выравнивание со и памяти O ( N , в отличие от библиотеки FastDTW . сложностью времени ) ² ) требование стандартного алгоритма DTW. FastDTW использует многоуровневый подход, который рекурсивно проецирует решение с более грубого разрешения и уточняет прогнозируемое решение.
• Форк FastDTW (Java) опубликован в Maven Central.
• time-series-classification (Java) — пакет для классификации временных рядов с использованием DTW в Weka.
• Пакет DTW предоставляет пакеты Python ( dtw-python ) и R ( dtw ) с полным охватом членов семейства алгоритмов DTW, включая различные правила рекурсии (также называемые шаблонами шагов), ограничения и сопоставление подстрок.
• Библиотека Python mlpy реализует DTW.
• Библиотека Python pydtw реализует меры DTW со вкусом Манхэттена и Евклида, включая нижние границы LB_Keogh.
• Библиотека cudadtw C++/CUDA реализует выравнивание подпоследовательностей DTW с евклидовым вкусом и z -нормализованное евклидово расстояние, аналогично популярному UCR-Suite на ускорителях с поддержкой CUDA.
• Библиотека машинного обучения JavaML реализует DTW .
• Библиотека ndtw C# реализует DTW с различными опциями.
• Sketch-a-Char использует Greedy DTW (реализованный в JavaScript) как часть программы классификатора символов LaTeX.
• MatchBox реализует DTW для сопоставления мел-частотных кепстральных коэффициентов аудиосигналов.
• Усреднение последовательности : реализация DBA на языке GPL Java.
• Набор инструментов распознавания жестов|GRT C++ для распознавания жестов в реальном времени реализует DTW.
• Пакет программного обеспечения PyHubs реализует DTW и классификаторы ближайших соседей, а также их расширения (классификаторы с поддержкой концентратора).
• Библиотека simpledtw Python реализует классический алгоритм динамического программирования O ( NM ) и основана на Numpy. Он поддерживает значения любого размера, а также использует пользовательские функции нормы для расстояний. Он лицензируется по лицензии MIT.
• Библиотека Python tslearn реализует DTW в контексте временных рядов.
• Библиотека Python cuTWED CUDA реализует современную улучшенную технологию Time Warp Edit Distance, используя только линейную память с феноменальным ускорением.
• DynamicAxisWarping.jl — это реализация DTW и связанных с ним алгоритмов Julia, таких как FastDTW, SoftDTW, GeneralDTW и барицентры DTW.
• Multi_DTW реализует DTW для сопоставления двух одномерных массивов или двухмерных речевых файлов (двумерный массив).
• DTAI Distance имеет реализации DTW на Python и C.

Приложения

Распознавание устной речи

Из-за разной скорости речи возникают нелинейные колебания структуры речи по отношению к оси времени, которые необходимо устранить. Сопоставление DP — это алгоритм сопоставления с образцом, основанный на динамическом программировании (DP) , который использует эффект нормализации времени, при котором колебания на оси времени моделируются с использованием нелинейной функции деформации времени. Рассматривая любые два речевых паттерна, мы можем избавиться от их временных различий, искривив ось времени одного так, чтобы было достигнуто максимальное совпадение с другим. Более того, если функции деформации разрешено принимать любое возможное значение, даже меньшее. можно провести различие между словами, принадлежащими к разным категориям. Так, чтобы усилить различие между словами, принадлежащими к разным категориям, были наложены ограничения на наклон функции деформации.

Корреляционный анализ мощности

Нестабильные часы используются для того, чтобы обойти наивный анализ мощности . Для противодействия этой защите используется несколько методов, одна из которых — динамическое искажение времени.

Финансы и эконометрика

Динамическое искажение времени используется в финансах и эконометрике для оценки качества прогнозов по сравнению с реальными данными.

См. также

• Расстояние Левенштейна
• Эластичное соответствие
• Выравнивание последовательности
• Множественное выравнивание последовательностей
• Алгоритм Вагнера-Фишера
• Алгоритм Нидлмана – Вунша
• Расстояние Фреше
• Нелинейная модель смешанных эффектов
• Графическое искажение времени

Дальнейшее чтение

• Павел Сенин, Обзор алгоритма динамического преобразования времени
• Vintsyuk, T. K. (1968). "Speech discrimination by dynamic programming". Kibernetika . 4 : 81–88.
• Сакоэ, Х.; Чиба (1978). «Оптимизация алгоритма динамического программирования для распознавания устной речи». Транзакции IEEE по акустике, речи и обработке сигналов . 26 (1): 43–49. дои : 10.1109/tassp.1978.1163055 . S2CID   17900407 .
• Майерс, CS; Рабинер, Л.Р. (1981). «Сравнительное исследование нескольких динамических алгоритмов преобразования времени для распознавания связанных слов». Технический журнал Bell System . 60 (7): 1389–1409. дои : 10.1002/j.1538-7305.1981.tb00272.x . ISSN   0005-8580 . S2CID   12857347 .
• Рабинер, Лоуренс; Хуанг, Биинг-Хван (1993). «Глава 4: Методы сравнения шаблонов». Основы распознавания речи . Энглвуд Клиффс, Нью-Джерси: PTR Prentice Hall. ISBN  978-0-13-015157-5 .
• Мюллер, Мейнард (2007). Динамическое искажение времени. В разделе «Поиск информации для музыки и движения», глава 4, страницы 69–84 (PDF) . Спрингер. дои : 10.1007/978-3-540-74048-3 . ISBN  978-3-540-74047-6 .
• Рактанманон, Танавин (сентябрь 2013 г.). «Обращение к временным рядам больших данных: анализ триллионов подпоследовательностей временных рядов в условиях динамического искажения времени» . Транзакции ACM по извлечению знаний из данных . 7 (3): 10:1–10:31. дои : 10.1145/2513092.2500489 . ПМК   6790126 . ПМИД   31607834 .