Временная последовательность

Временной ряд: случайные данные плюс тренд, с линией наилучшего соответствия и различными применяемыми фильтрами.

В математике временной ряд — это ряд точек данных, проиндексированных (или перечисленных, или представленных на графике) во временном порядке. Чаще всего временной ряд представляет собой последовательность , полученную в последовательные равноотстоящие друг от друга моменты времени. Таким образом, это последовательность данных дискретного времени . Примерами временных рядов являются высота океанских приливов , количество солнечных пятен и дневное значение промышленного индекса Доу-Джонса .

Временной ряд очень часто строится с помощью диаграммы прогона (которая представляет собой временную линейную диаграмму ). Временные ряды используются в статистике , обработке сигналов , распознавании образов , эконометрике , математических финансах , прогнозировании погоды , предсказании землетрясений , электроэнцефалографии , технике управления , астрономии , технике связи и, в основном, в любой области прикладной науки и техники , которая включает временные измерения.

временных рядов Анализ включает методы анализа данных временных рядов с целью извлечения значимой статистики и других характеристик данных. временных рядов Прогнозирование — это использование модели для прогнозирования будущих значений на основе ранее наблюдаемых значений. Хотя регрессионный анализ часто используется для проверки взаимосвязей между одним или несколькими различными временными рядами, этот тип анализа обычно не называют «анализом временных рядов», который относится, в частности, к взаимосвязям между различными моментами времени в пределах одного ряд.

Данные временных рядов имеют естественный временной порядок. Это отличает анализ временных рядов от перекрестных исследований , в которых нет естественного порядка наблюдений (например, объяснение заработной платы людей со ссылкой на их соответствующие уровни образования, где данные отдельных лиц могут быть введены в любом порядке). Анализ временных рядов также отличается от анализа пространственных данных , где наблюдения обычно относятся к географическим местоположениям (например, учет цен на жилье по местоположению, а также внутренним характеристикам домов). Стохастическая . модель временного ряда обычно отражает тот факт, что наблюдения, расположенные близко друг к другу во времени, будут более тесно связаны, чем наблюдения, расположенные дальше друг от друга Кроме того, модели временных рядов часто используют естественное одностороннее упорядочение времени, так что значения за данный период будут выражены как вытекающие каким-то образом из прошлых значений, а не из будущих значений (см. обратимость времени ).

Анализ временных рядов может применяться к действительным , непрерывным данным, дискретным числовым данным или дискретным символическим данным (т. е. последовательностям символов, таких как буквы и слова на английском языке). ^[1]).

Методы анализа [ править ]

Методы анализа временных рядов можно разделить на два класса: методы частотной области и методы временной области . Первые включают спектральный анализ и вейвлет-анализ ; последние включают автокорреляционный и кросскорреляционный анализ. Во временной области корреляция и анализ могут выполняться подобно фильтру с использованием масштабированной корреляции , тем самым уменьшая необходимость работы в частотной области.

Кроме того, методы анализа временных рядов можно разделить на параметрические и непараметрические методы. Параметрические подходы предполагают, что лежащий в основе стационарный случайный процесс имеет определенную структуру, которую можно описать с помощью небольшого числа параметров (например, с помощью модели авторегрессии или модели скользящего среднего ). В этих подходах задачей является оценка параметров модели, описывающей случайный процесс. Напротив, непараметрические подходы явно оценивают ковариацию или спектр процесса, не предполагая, что процесс имеет какую-либо конкретную структуру.

Методы анализа временных рядов также можно разделить на линейные и нелинейные , одномерные и многомерные .

Панельные данные [ править ]

Временной ряд — это один из типов панельных данных . Панельные данные — это общий класс, многомерный набор данных, тогда как набор данных временных рядов представляет собой одномерную панель (как и набор поперечных данных ). Набор данных может демонстрировать характеристики как панельных данных, так и данных временных рядов. Один из способов узнать это — спросить, что делает одну запись данных уникальной среди других записей. Если ответом является поле временных данных, то это кандидат на набор данных временных рядов. Если для определения уникальной записи требуется поле данных времени и дополнительный идентификатор, не связанный со временем (например, идентификатор студента, биржевой символ, код страны), тогда она является кандидатом на панельные данные. Если дифференциация основана на невременном идентификаторе, то набор данных является кандидатом на набор перекрестных данных.

Анализ [ править ]

Существует несколько типов мотивации и анализа данных для временных рядов, которые подходят для разных целей.

Мотивация [ править ]

В контексте статистики , эконометрики , количественных финансов , сейсмологии , метеорологии и геофизики основной целью анализа временных рядов является прогнозирование . В контексте обработки сигналов , техники управления и связи он используется для обнаружения сигналов. Другие приложения относятся к интеллектуальному анализу данных , распознаванию образов и машинному обучению , где анализ временных рядов может использоваться для кластеризации . ^[2]^[3] классификация , ^[4] запрос по содержанию, ^[5] обнаружение аномалий , а также прогнозирование . ^[6]

Разведочный анализ [ править ]

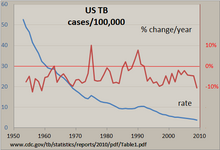
Самый простой способ изучить регулярный временной ряд — вручную с помощью линейного графика . Справа показан пример диаграммы заболеваемости туберкулезом в США, составленной с помощью программы электронных таблиц. Число случаев было стандартизировано по показателю на 100 000 и рассчитано процентное изменение этого показателя за год. Почти устойчиво нисходящая линия показывает, что заболеваемость туберкулезом снижалась в большинстве лет, но процентное изменение этого показателя варьировалось в пределах +/- 10%, с «всплесками» в 1975 году и примерно в начале 1990-х годов. Использование обеих вертикальных осей позволяет сравнивать два временных ряда на одном графике.

Исследование, проведенное аналитиками корпоративных данных, обнаружило две проблемы при исследовательском анализе временных рядов: обнаружение формы интересных закономерностей и поиск объяснения этих закономерностей. ^[7] Визуальные инструменты, представляющие данные временных рядов в виде матриц тепловых карт, могут помочь преодолеть эти проблемы.

Другие методы включают в себя:

Автокорреляционный анализ для изучения серийной зависимости
Спектральный анализ для изучения циклического поведения, которое не обязательно связано с сезонностью . Например, активность солнечных пятен варьируется в течение 11-летних циклов. ^[8]^[9] Другие распространенные примеры включают небесные явления, погодные условия, нейронную активность, цены на сырьевые товары и экономическую активность.
Разделение на компоненты, представляющие тренд, сезонность, медленные и быстрые изменения и циклическую неравномерность: см. оценку тренда и разложение временных рядов .

Подгонка кривой [ править ]

Подгонка кривой ^[10]^[11] это процесс построения кривой или математической функции , которая лучше всего соответствует ряду точек данных , ^[12] возможно, с учетом ограничений. ^[13]^[14] Аппроксимация кривой может включать в себя либо интерполяцию , либо ^[15]^[16] где требуется точное соответствие данным или сглаживание , ^[17]^[18]в котором строится «гладкая» функция, приблизительно соответствующая данным. Связанная тема — регрессионный анализ . ^[19]^[20]который больше фокусируется на вопросах статистического вывода , таких как степень неопределенности в кривой, которая соответствует данным, наблюдаемым со случайными ошибками. Встроенные кривые можно использовать в качестве вспомогательного средства для визуализации данных. ^[21]^[22] вывести значения функции при отсутствии данных, ^[23] и суммировать отношения между двумя или более переменными. ^[24] Экстраполяция означает использование подобранной кривой за пределами диапазона наблюдаемых данных. ^[25] и подвержен определенной степени неопределенности ^[26] поскольку он может отражать метод, использованный для построения кривой, в такой же степени, как и наблюдаемые данные.

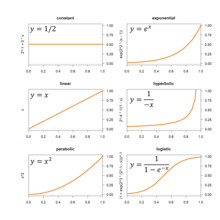
Для процессов, масштабы которых, как ожидается, обычно будут расти, одну из кривых на графике справа (и многих других) можно аппроксимировать путем оценки их параметров.

Построение экономических временных рядов предполагает оценку некоторых компонентов на некоторые даты путем интерполяции между значениями («бенчмарками») на более ранние и более поздние даты. Интерполяция — это оценка неизвестной величины между двумя известными величинами (историческими данными) или получение выводов об недостающей информации на основе имеющейся информации («чтение между строк»). ^[27]Интерполяция полезна, когда доступны данные, относящиеся к отсутствующим данным, и известны их тенденции, сезонность и долгосрочные циклы. Это часто делается с использованием связанного ряда, известного по всем соответствующим датам. ^[28]В качестве альтернативы полиномиальная интерполяция или сплайн-интерполяция используется , когда кусочно -полиномиальные функции вписываются во временные интервалы так, что они плавно совмещаются друг с другом. Другая проблема, тесно связанная с интерполяцией, — это аппроксимация сложной функции простой функцией (также называемой регрессией ). Основное различие между регрессией и интерполяцией заключается в том, что полиномиальная регрессия дает один полином, который моделирует весь набор данных. Однако сплайн-интерполяция дает кусочно-непрерывную функцию, состоящую из множества полиномов, для моделирования набора данных.

Экстраполяция — это процесс оценки значения переменной за пределами исходного диапазона наблюдения на основе ее связи с другой переменной. Это похоже на интерполяцию , которая дает оценки между известными наблюдениями, но экстраполяция подвержена большей неопределенности и более высокому риску получения бессмысленных результатов.

Аппроксимация функции [ править ]

В общем, задача аппроксимации функции требует от нас выбрать функцию среди четко определенного класса, которая точно соответствует («приближает») целевой функции способом, специфичным для конкретной задачи. Можно выделить два основных класса задач аппроксимации функций: во-первых, для известных целевых функций теория аппроксимации — это раздел численного анализа , который исследует, как определенные известные функции (например, специальные функции ) могут быть аппроксимированы определенным классом функций (для например, полиномы или рациональные функции ), которые часто обладают желаемыми свойствами (недорогие вычисления, непрерывность, целые и предельные значения и т. д.).

Во-вторых, целевая функция, назовем ее g , может быть неизвестна; только набор точек (временной ряд) вида ( x , g ( x вместо явной формулы предоставляется )) В зависимости от структуры домена и кодомена g могут g методов аппроксимации несколько быть применимы . Например, если g — операция над действительными числами методы интерполяции , экстраполяции , регрессионного анализа и подбора кривой , можно использовать . Если кодомен (диапазон или целевой набор) g является конечным множеством, вместо этого приходится иметь дело с проблемой классификации . Связанная проблема онлайн- аппроксимации временных рядов ^[29] заключается в суммировании данных за один проход и построении приблизительного представления, которое может поддерживать различные запросы временных рядов с границами наихудшей ошибки.

В некоторой степени различные проблемы ( регрессия , классификация , аппроксимация приспособленности ) получили единое рассмотрение в статистической теории обучения , где они рассматриваются как проблемы обучения с учителем .

Прогнозирование и прогнозирование [ править ]

В статистике предсказание является частью статистического вывода . Один конкретный подход к такому выводу известен как прогнозирующий вывод , но прогноз может быть выполнен в рамках любого из нескольких подходов к статистическому выводу. Действительно, одно из описаний статистики заключается в том, что она обеспечивает средство передачи знаний об выборке совокупности всей совокупности и другим связанным популяциям, что не обязательно совпадает с прогнозированием с течением времени. Когда информация передается во времени, часто в определенные моменты времени, этот процесс известен как прогнозирование .

Полностью сформированные статистические модели для целей стохастического моделирования , позволяющие генерировать альтернативные версии временных рядов, представляющие то, что может произойти в неопределенные периоды времени в будущем.
Простые или полностью сформированные статистические модели для описания вероятного результата временного ряда в ближайшем будущем при условии знания самых последних результатов (прогнозирование).
Прогнозирование по временным рядам обычно выполняется с использованием пакетов автоматизированного статистического программного обеспечения и языков программирования, таких как Julia , Python , R , SAS , SPSS и многих других.
Прогнозирование крупномасштабных данных можно выполнить с помощью Apache Spark, используя библиотеку Spark-TS, сторонний пакет. ^[30]

Классификация [ править ]

Присвоение шаблона временного ряда определенной категории, например, определение слова на основе серии движений рук на языке жестов .

Оценка сигнала [ править ]

Этот подход основан на гармоническом анализе и фильтрации сигналов в частотной области с использованием преобразования Фурье и оценке спектральной плотности , развитие которых было значительно ускорено во время Второй мировой войны математиком Норбертом Винером , инженерами-электриками Рудольфом Э. Кальманом , Деннисом Габором. и другие для фильтрации сигналов от шума и прогнозирования значений сигналов в определенный момент времени. См. Фильтр Калмана , Теорию оценки и Цифровую обработку сигналов.

Сегментация [ править ]

Разбиение временного ряда на последовательность сегментов. Часто временной ряд можно представить как последовательность отдельных сегментов, каждый из которых имеет свои характерные свойства. Например, аудиосигнал конференц-связи можно разделить на части, соответствующие времени, в течение которого говорил каждый человек. Цель сегментации временных рядов состоит в том, чтобы идентифицировать граничные точки сегментов во временных рядах и охарактеризовать динамические свойства, связанные с каждым сегментом. К этой проблеме можно подойти, используя обнаружение точки изменения или моделируя временной ряд как более сложную систему, такую как линейная система с марковским скачком.

Кластеризация [ править ]

Данные временных рядов могут быть кластеризованы, однако при рассмотрении кластеризации подпоследовательностей необходимо проявлять особую осторожность. ^[31] Кластеризацию временных рядов можно разделить на

кластеризация целых временных рядов (несколько временных рядов, для которых нужно найти кластер)
кластеризация временных рядов подпоследовательностей (одиночные временные ряды, разделенные на фрагменты с использованием скользящих окон)
кластеризация моментов времени

временных подпоследовательностей Кластеризация рядов

Кластеризация временных рядов подпоследовательностей привела к образованию нестабильных (случайных) кластеров, вызванных выделением признаков с использованием фрагментации со скользящими окнами. ^[32]Было обнаружено, что центры кластеров (среднее значение временного ряда в кластере — также временной ряд) следуют произвольно сдвинутой синусоидальной схеме (независимо от набора данных, даже при реализациях случайного блуждания ) . Это означает, что найденные центры кластеров не являются описательными для набора данных, поскольку центры кластеров всегда представляют собой нерепрезентативные синусоидальные волны.

Модели [ править ]

Модели данных временных рядов могут иметь множество форм и представлять различные случайные процессы . При моделировании изменений уровня процесса практическое значение имеют три широких класса: модели авторегрессии (AR), интегрированные модели (I) и модели скользящего среднего (MA). Эти три класса линейно зависят от предыдущих точек данных. ^[33]Комбинация этих идей приводит к созданию моделей авторегрессионного скользящего среднего (ARMA) и авторегрессионного интегрированного скользящего среднего (ARIMA). Модель авторегрессионного дробно-интегрированного скользящего среднего (ARFIMA) обобщает первые три. Расширения этих классов для работы с векторными данными доступны под заголовком многомерных моделей временных рядов, а иногда предыдущие аббревиатуры расширяются за счет включения начальной буквы «V» для «вектора», как в VAR для векторной авторегрессии . Дополнительный набор расширений этих моделей доступен для использования там, где наблюдаемый временной ряд определяется некоторыми «вынуждающими» временными рядами (которые могут не оказывать причинного влияния на наблюдаемый ряд): отличие от многомерного случая состоит в том, что ряд воздействия может быть детерминированным или находиться под контролем экспериментатора. Для этих моделей аббревиатуры дополняются последней буквой «X», обозначающей «экзогенный».

Нелинейная зависимость уровня ряда от предыдущих точек данных представляет интерес, отчасти из-за возможности создания хаотического временного ряда. Однако, что еще более важно, эмпирические исследования могут указать на преимущество использования прогнозов, полученных на основе нелинейных моделей, по сравнению с предсказаниями, полученными на основе линейных моделей, как, например, в нелинейных авторегрессионных экзогенных моделях . Дополнительные ссылки по нелинейному анализу временных рядов: (Канц и Шрайбер), ^[34] и (Абарбанель) ^[35]

Среди других типов моделей нелинейных временных рядов есть модели, представляющие изменения дисперсии во времени ( гетерскедастичность ). Эти модели представляют собой авторегрессионную условную гетероскедастичность (ARCH), и коллекция включает в себя широкий спектр представлений ( GARCH , TARCH, EGARCH, FigARCH, CGARCH и т. д.). Здесь изменения изменчивости связаны с недавними прошлыми значениями наблюдаемого ряда или предсказываются ими. Это контрастирует с другими возможными представлениями локально изменяющейся изменчивости, где изменчивость может быть смоделирована как обусловленная отдельным изменяющимся во времени процессом, как в дважды стохастической модели .

В недавних работах по безмодельному анализу популярность получили методы, основанные на вейвлет-преобразовании (например, локально стационарные вейвлеты и нейронные сети с вейвлет-разложением). Методы мультимасштаба (часто называемые мультиразрешением) разлагают заданный временной ряд, пытаясь проиллюстрировать временную зависимость в нескольких масштабах. См. также методы мультифрактального переключения Маркова (MSMF) для моделирования эволюции волатильности.

( Скрытая марковская модель СММ) — статистическая марковская модель, в которой моделируемая система рассматривается как марковский процесс с ненаблюдаемыми (скрытыми) состояниями. HMM можно рассматривать как простейшую динамическую байесовскую сеть . Модели HMM широко используются в распознавании речи для перевода временного ряда произнесенных слов в текст.

Многие из этих моделей собраны в пакете Python sktime .

Обозначения [ править ]

Для анализа временных рядов используется ряд различных обозначений. Обычное обозначение, определяющее временной ряд X , индексируемый натуральными числами, записывается:

Икс = ( Икс ₁ , Икс ₂ , ...).

Другое распространенное обозначение

Y знак равно ( Y _т : т ∈ Т ),

где T — набор индексов .

Условия [ править ]

Есть два набора условий, при которых строится большая часть теории:

Эргодичность подразумевает стационарность, но обратное не обязательно так. Стационарность обычно подразделяют на строгую стационарность и стационарность в широком смысле или стационарность второго порядка . При каждом из этих условий могут быть разработаны как модели, так и приложения, хотя в последнем случае модели можно считать лишь частично уточненными.

Кроме того, анализ временных рядов может применяться в тех случаях, когда ряды являются сезонно стационарными или нестационарными. Ситуации, когда амплитуды частотных составляющих изменяются со временем, можно рассматривать с помощью частотно-временного анализа , который использует частотно-временное представление временного ряда или сигнала. ^[36]

Инструменты [ править ]

Инструменты для исследования данных временных рядов включают в себя:

Учет автокорреляционной функции и функции спектральной плотности (также функций взаимной корреляции и функций взаимной спектральной плотности)
Масштабированные функции взаимной и автокорреляции для устранения влияния медленных компонентов. ^[37]
Выполнение преобразования Фурье для исследования ряда в частотной области
Дискретные, непрерывные или смешанные спектры временных рядов в зависимости от того, содержит ли временной ряд (обобщенный) гармонический сигнал или нет.
Использование фильтра для удаления нежелательного шума.
Анализ главных компонент (или ортогональных функций ) эмпирический анализ
Анализ сингулярного спектра
«Структурные» модели:
- общего состояния Космические модели
- Модели ненаблюдаемых компонентов
Машинное обучение
теории массового обслуживания Анализ
Контрольная карта
- Индивидуальная контрольная карта Шухарта
- КУСУМ Диаграмма
- Диаграмма EWMA
Анализ колебаний без тренда
Нелинейное моделирование смешанных эффектов
Динамическое искажение времени ^[38]
Динамическая байесовская сеть
Методы частотно-временного анализа:
Хаотический анализ

Меры [ править ]

временных рядов Метрики или функции , которые можно использовать для классификации временных рядов или регрессионного анализа : ^[39]

Одномерные линейные меры
- Момент (математика)
- Спектральная мощность полосы
- Спектральная граничная частота
- Накопленная энергия (обработка сигнала)
- Характеристики автокорреляционной функции
- Параметры Хьорта
- БПФ Параметры
- авторегрессионной модели Параметры
- Тест Манна-Кендалла
Одномерные нелинейные меры
- Меры, основанные на корреляционной сумме
- Измерение корреляции
- Корреляционный интеграл
- Плотность корреляции
- Корреляционная энтропия
- Приблизительная энтропия ^[40]
- Выборочная энтропия
- Энтропия Фурье [ великобритания ]
- Вейвлет-энтропия
- Дисперсионная энтропия
- Энтропия дисперсии флуктуаций
- Энтропия Реньи
- Методы высшего порядка
- Предельная предсказуемость
- динамического сходства Индекс
- пространства состояний Меры несходства
- Lyapunov exponent
- Методы перестановки
- Местный поток
Другие одномерные меры
- Алгоритмическая сложность
- Колмогоровские оценки сложности
- марковской модели Скрытые состояния
- Подпись трудного пути ^[41]
- Суррогатные временные ряды и суррогатная коррекция
- Потеря повторяемости (степень нестационарности)
Двумерные линейные меры
- Максимальная линейная взаимная корреляция
- Линейная когерентность (обработка сигналов)
Двумерные нелинейные меры
- Нелинейная взаимозависимость
- Динамическое смещение (физика)
- Меры по фазовой синхронизации
- Меры по фазовой синхронизации
Меры сходства : ^[42]
- Взаимная корреляция
- Динамическое искажение времени ^[38]
- Скрытая модель Маркова
- Изменить расстояние
- Общая корреляция
- Оценщик Ньюи – Уэста
- Преобразование Прайса – Уинстена
- Данные как векторы в метризуемом пространстве
  - Расстояние Минковского
  - Расстояние Махаланобис
- Данные в виде временных рядов с конвертами
  - Глобальное стандартное отклонение
  - Локальное стандартное отклонение
  - Окно стандартного отклонения
- Данные интерпретируются как стохастический ряд
  - Коэффициент корреляции момента произведения Пирсона
  - Коэффициент ранговой корреляции Спирмена
- Данные интерпретируются как распределения вероятностей. функция
  - Тест Колмогорова – Смирнова
  - Критерий Крамера-фон Мизеса

Визуализация [ править ]

Временные ряды можно визуализировать с помощью диаграмм двух категорий: перекрывающиеся диаграммы и отдельные диаграммы. На перекрывающихся диаграммах все временные ряды отображаются в одном макете, тогда как на отдельных диаграммах они представлены в разных макетах (но выровнены для целей сравнения). ^[43]

Перекрывающиеся диаграммы [ править ]

Плетеные графы
Линейные графики
Графики наклона
Диаграмма разрывов [ фр ]

Отдельные диаграммы [ править ]

Графики горизонтов
Уменьшенная линейная диаграмма (малые кратные)
График силуэта
Круговой силуэт

См. также [ править ]

Ссылки [ править ]

^ Лин, Джессика; Кио, Имонн; Лонарди, Стефано; Чиу, Билл (2003). «Символическое представление временных рядов, имеющее значение для алгоритмов потоковой передачи». Материалы 8-го семинара ACM SIGMOD по вопросам исследований в области интеллектуального анализа данных и открытия знаний . Нью-Йорк: ACM Press. стр. 2–11. CiteSeerX 10.1.1.14.5597 . дои : 10.1145/882082.882086 . ISBN 9781450374224 . S2CID 6084733 .
^ Уоррен Ляо, Т. (ноябрь 2005 г.). «Кластеризация данных временных рядов — опрос». Распознавание образов . 38 (11): 1857–1874. Бибкод : 2005PatRe..38.1857W . дои : 10.1016/j.patcog.2005.01.025 . S2CID 8973749 .
^ Агабозорги, Саид; Сейед Ширхоршиди, Али; Ин Ва, Тех (октябрь 2015 г.). «Кластеризация временных рядов - десятилетний обзор». Информационные системы . 53 : 16–38. дои : 10.1016/j.is.2015.04.007 . S2CID 158707 .
^ Кио, Имонн; Касетти, Шрути (2002). «О необходимости критериев интеллектуального анализа данных временных рядов: опрос и эмпирическая демонстрация». Материалы восьмой международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных . стр. 102–111. дои : 10.1145/775047.775062 . ISBN 1-58113-567-Х .
^ Агравал, Ракеш; Фалуцсос, Христос; Свами, Арун (1993). «Эффективный поиск сходства в базах данных последовательностей». Основы организации данных и алгоритмы . Конспекты лекций по информатике. Том. 730. стр. 69–84. дои : 10.1007/3-540-57301-1_5 . ISBN 978-3-540-57301-2 . S2CID 16748451 .
^ Чен, Кэти В.С.; Чиу, LM (4 сентября 2021 г.). «Прогнозирование порядкового временного ряда индекса качества воздуха» . Энтропия . 23 (9): 1167. Бибкод : 2021Entrp..23.1167C . дои : 10.3390/e23091167 . ПМЦ 8469594 . ПМИД 34573792 .
^ Саркар, Адвайт; Спотт, Мартин; Блэквелл, Алан Ф.; Ямник, Матея (2016). «Визуальное обнаружение и модельное объяснение закономерностей временных рядов» . Симпозиум IEEE 2016 по визуальным языкам и человеко-ориентированным вычислениям (VL/HCC) . стр. 78–86. дои : 10.1109/vlhcc.2016.7739668 . ISBN 978-1-5090-0252-8 . S2CID 9787931 .
^ Блумфилд, Питер (1976). Фурье-анализ временных рядов: введение . Уайли. ISBN 978-0-471-08256-9 . ^{[ нужна страница ]}
^ Шамуэй, Роберт Х. (1988). Прикладной статистический анализ временных рядов . Прентис-Холл. ISBN 978-0-13-041500-4 . ^{[ нужна страница ]}
^ Арлингхаус, Сандра (1994). Практическое руководство по подбору кривых . ЦРК Пресс. ISBN 978-0-8493-0143-8 . ^{[ нужна страница ]}
^ Колб, Уильям М. (1984). Аппроксимация кривой для программируемых калькуляторов . СИНТЕК. ISBN 978-0-943494-02-9 . ^{[ нужна страница ]}
^ Халли, СС; Рао, К.В. (1992). Передовые методы демографического анализа . Springer Science & Business Media. п. 165. ИСБН 978-0-306-43997-1 . Функции выполняются, если у нас есть хорошее или умеренное соответствие наблюдаемым данным.
^ Сигнал и шум : почему так много прогнозов не работают, а некоторые нет. Нейт Сильвер
^ Пайл, Дориан (1999). Подготовка данных для интеллектуального анализа данных . Морган Кауфманн. ISBN 978-1-55860-529-9 . ^{[ нужна страница ]}
^ Численные методы в инженерии с MATLAB®. Автор Яан Киусалас . Страница 24.
^ Киусалас, Яан (2013). Численные методы в проектировании с использованием Python 3 . Издательство Кембриджского университета. п. 21. ISBN 978-1-139-62058-1 .
^ Гость, Филип Джордж (2012). Численные методы аппроксимации кривой . Издательство Кембриджского университета. п. 349. ИСБН 978-1-107-64695-7 .
^ См. Также: Моллифер
^ Мотульский, Харви; Христопулос, Артур (2004). Подгонка моделей к биологическим данным с использованием линейной и нелинейной регрессии: практическое руководство по подгонке кривой . Издательство Оксфордского университета. ISBN 978-0-19-803834-4 . ^{[ нужна страница ]}
^ Регрессионный анализ Рудольфа Дж. Фройнда, Уильяма Дж. Уилсона, Ping Sa. Страница 269. ^{[ дата отсутствует ]}
^ Дауд, Ханита; Сагаян, Виджант; Яхья, Нурхана; Наджвати, Ван (2009). «Моделирование электромагнитных волн с использованием статистических и численных методов». Визуальная информатика: соединение исследований и практики . Конспекты лекций по информатике. Том. 5857. стр. 686–695. дои : 10.1007/978-3-642-05036-7_65 . ISBN 978-3-642-05035-0 .
^ Хаузер, Джон Р. (2009). Численные методы для нелинейных инженерных моделей . Springer Science & Business Media. п. 227. ИСБН 978-1-4020-9920-5 .
^ Уильям, Дадли, изд. (1976). «Ядерная и атомная спектроскопия». Спектроскопия . Методы экспериментальной физики. Том. 13. С. 115–346 [150]. дои : 10.1016/S0076-695X(08)60643-2 . ISBN 978-0-12-475913-8 .
^ Салкинд, Нил Дж. (2010). Энциклопедия дизайна исследований . МУДРЕЦ. п. 266. ИСБН 978-1-4129-6127-1 .
^ Клостерман, Ричард Э. (1990). Методы анализа и планирования сообщества . Издательство Rowman & Littlefield. п. 1. ISBN 978-0-7425-7440-3 .
^ Йо, Чарльз Э. (март 1996 г.). Введение в риск и неопределенность в оценке экологических инвестиций (Отчет). Инженерный корпус армии США. п. 69. ДТИК АДА316839 .
^ Хэмминг, Ричард (2012). Численные методы для ученых и инженеров . Курьерская корпорация. ISBN 978-0-486-13482-6 . ^{[ нужна страница ]}
^ Фридман, Милтон (декабрь 1962 г.). «Интерполяция временных рядов связанными рядами». Журнал Американской статистической ассоциации . 57 (300): 729–757. дои : 10.1080/01621459.1962.10500812 .
^ Ганди, Сораб; Фоскини, Лука; Сури, Субхаш (2010). «Экономичное онлайн-аппроксимирование данных временных рядов: потоки, амнезия и нарушение порядка». 2010 26-я Международная конференция IEEE по инженерии данных (ICDE 2010) . стр. 924–935. дои : 10.1109/ICDE.2010.5447930 . ISBN 978-1-4244-5445-7 . S2CID 16072352 .
^ Сэнди Риза (18 марта 2020 г.). «Анализ временных рядов с помощью Spark» (слайды доклада на Spark Summit East 2016) . Блоки данных . Проверено 12 января 2021 г.
^ Золхавари, Сейеджамаль; Агабозорги, Саид; Тэ, Ин Ва (2014). «Обзор кластеризации временных рядов подпоследовательностей» . Научный мировой журнал . 2014 : 312521. дои : 10.1155/2014/312521 . ПМК 4130317 . ПМИД 25140332 .
^ Кио, Имонн; Лин, Джессика (август 2005 г.). «Кластеризация подпоследовательностей временных рядов бессмысленна: последствия для предыдущих и будущих исследований». Знания и информационные системы . 8 (2): 154–177. дои : 10.1007/s10115-004-0172-7 .
^ Гершенфельд, Н. (1999). Природа математического моделирования . Нью-Йорк: Издательство Кембриджского университета. стр. 205–208 . ISBN 978-0521570954 .
^ Канц, Хольгер; Томас, Шрайбер (2004). Нелинейный анализ временных рядов . Лондон: Издательство Кембриджского университета. ISBN 978-0521529020 .
^ Абарбанель, Генри (25 ноября 1997 г.). Анализ наблюдаемых хаотических данных . Нью-Йорк: Спрингер. ISBN 978-0387983721 .
^ Боашаш, Б. (редактор), (2003) Частотно-временной анализ и обработка сигналов: полный справочник , Elsevier Science, Оксфорд, 2003. ISBN 0-08-044335-4
^ Николич, Данко; Мурешан, Рауль К.; Фэн, Вэйцзя; Певец Вольф (март 2012 г.). «Масштабный корреляционный анализ: лучший способ вычисления кросс-коррелограммы». Европейский журнал неврологии . 35 (5): 742–762. дои : 10.1111/j.1460-9568.2011.07987.x . ПМИД 22324876 . S2CID 4694570 .
^ Перейти обратно: ^а ^б Сакоэ, Х.; Чиба, С. (февраль 1978 г.). «Оптимизация алгоритма динамического программирования для распознавания устной речи». Транзакции IEEE по акустике, речи и обработке сигналов . 26 (1): 43–49. дои : 10.1109/ТАССП.1978.1163055 . S2CID 17900407 .
^ Морманн, Флориан; Анджейак, Ральф Г.; Элджер, Кристиан Э.; Ленертц, Клаус (2007). «Прогнозирование приступов: долгий и извилистый путь» . Мозг . 130 (2): 314–333. дои : 10.1093/brain/awl241 . ПМИД 17008335 .
^ Лэнд, Брюс; Элиас, Дамиан. «Измерение сложности временного ряда» .
^ Чевырев Илья; Кормилицин, Андрей (2016). «Букварь по методу сигнатур в машинном обучении». arXiv : 1603.03788 .
^ Ропелла, GEP; Наг, Д.А.; Хант, Калифорния (2003). «Меры сходства для автоматического сравнения результатов экспериментов in silico и in vitro». Материалы 25-й ежегодной международной конференции Общества инженеров в медицине и биологии IEEE (номер по каталогу IEEE 03CH37439) . стр. 2933–2936. дои : 10.1109/IEMBS.2003.1280532 . ISBN 978-0-7803-7789-9 . S2CID 17798157 .
^ Томински, Кристиан; Айгнер, Вольфганг. «Браузер TimeViz: визуальный обзор методов визуализации данных, ориентированных на время» . Проверено 1 июня 2014 г.

Дальнейшее чтение [ править ]

Де Гойер, Ян Г.; Гайндман, Роб Дж. (2006). «25 слез прогнозирования временных рядов». Международный журнал прогнозирования . Двадцать пять лет прогнозирования. 22 (3): 443–473. CiteSeerX 10.1.1.154.9227 . doi : 10.1016/j.ijforecast.2006.01.001 . S2CID 14996235 .
Бокс, Джордж ; Дженкинс, Гвилим (1976), Анализ временных рядов: прогнозирование и контроль, ред. ред. , Окленд, Калифорния: Холден-Дэй
Дурбин Дж. , Купман С.Дж. (2001), Анализ временных рядов методами пространства состояний , Oxford University Press .
Гершенфельд, Нил (2000), Природа математического моделирования , издательство Кембриджского университета , ISBN 978-0-521-57095-4 , OCLC 174825352
Гамильтон, Джеймс (1994), Анализ временных рядов , Princeton University Press , ISBN 978-0-691-04289-3
Пристли, МБ (1981), Спектральный анализ и временные ряды , Academic Press . ISBN 978-0-12-564901-8
Шаша, Д. (2004), Высокопроизводительное открытие во временных рядах , Springer , ISBN 978-0-387-00857-8
Шамуэй Р.Х., Стоффер Д.С. (2017), Анализ временных рядов и его приложения: на примерах R (изд. 4) , Springer, ISBN 978-3-319-52451-1
Вейгенд А.С., Гершенфельд Н.А. (ред.) (1994), Прогнозирование временных рядов: прогнозирование будущего и понимание прошлого . Труды семинара перспективных исследований НАТО по сравнительному анализу временных рядов (Санта-Фе, май 1992 г.), Аддисон-Уэсли .
Винер, Н. (1949), Экстраполяция, интерполяция и сглаживание стационарных временных рядов , MIT Press .
Вудворд, Вашингтон, Грей, Х.Л. и Эллиотт, AC (2012), Прикладной анализ временных рядов , CRC Press .
Ауффарт, Бен (2021). Машинное обучение для временных рядов с помощью Python: прогнозирование, предсказание и обнаружение аномалий с помощью современных методов машинного обучения (1-е изд.). Пакт Паблишинг. ISBN 978-1801819626 . Проверено 5 ноября 2021 г.

Внешние ссылки [ править ]

Введение в анализ временных рядов (Справочник по инженерной статистике) — практическое руководство по анализу временных рядов.

[1] Лин, Джессика; Кио, Имонн; Лонарди, Стефано; Чиу, Билл (2003). «Символическое представление временных рядов, имеющее значение для алгоритмов потоковой передачи». Материалы 8-го семинара ACM SIGMOD по вопросам исследований в области интеллектуального анализа данных и открытия знаний . Нью-Йорк: ACM Press. стр. 2–11. CiteSeerX 10.1.1.14.5597 . дои : 10.1145/882082.882086 . ISBN 9781450374224 . S2CID 6084733 .

[2] Уоррен Ляо, Т. (ноябрь 2005 г.). «Кластеризация данных временных рядов — опрос». Распознавание образов . 38 (11): 1857–1874. Бибкод : 2005PatRe..38.1857W . дои : 10.1016/j.patcog.2005.01.025 . S2CID 8973749 .

[3] Агабозорги, Саид; Сейед Ширхоршиди, Али; Ин Ва, Тех (октябрь 2015 г.). «Кластеризация временных рядов - десятилетний обзор». Информационные системы . 53 : 16–38. дои : 10.1016/j.is.2015.04.007 . S2CID 158707 .

[4] Кио, Имонн; Касетти, Шрути (2002). «О необходимости критериев интеллектуального анализа данных временных рядов: опрос и эмпирическая демонстрация». Материалы восьмой международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных . стр. 102–111. дои : 10.1145/775047.775062 . ISBN 1-58113-567-Х .

[5] Агравал, Ракеш; Фалуцсос, Христос; Свами, Арун (1993). «Эффективный поиск сходства в базах данных последовательностей». Основы организации данных и алгоритмы . Конспекты лекций по информатике. Том. 730. стр. 69–84. дои : 10.1007/3-540-57301-1_5 . ISBN 978-3-540-57301-2 . S2CID 16748451 .

[6] Чен, Кэти В.С.; Чиу, LM (4 сентября 2021 г.). «Прогнозирование порядкового временного ряда индекса качества воздуха» . Энтропия . 23 (9): 1167. Бибкод : 2021Entrp..23.1167C . дои : 10.3390/e23091167 . ПМЦ 8469594 . ПМИД 34573792 .

[7] Саркар, Адвайт; Спотт, Мартин; Блэквелл, Алан Ф.; Ямник, Матея (2016). «Визуальное обнаружение и модельное объяснение закономерностей временных рядов» . Симпозиум IEEE 2016 по визуальным языкам и человеко-ориентированным вычислениям (VL/HCC) . стр. 78–86. дои : 10.1109/vlhcc.2016.7739668 . ISBN 978-1-5090-0252-8 . S2CID 9787931 .

[8] Блумфилд, Питер (1976). Фурье-анализ временных рядов: введение . Уайли. ISBN 978-0-471-08256-9 . ^{[ нужна страница ]}

[9] Шамуэй, Роберт Х. (1988). Прикладной статистический анализ временных рядов . Прентис-Холл. ISBN 978-0-13-041500-4 . ^{[ нужна страница ]}

[10] Арлингхаус, Сандра (1994). Практическое руководство по подбору кривых . ЦРК Пресс. ISBN 978-0-8493-0143-8 . ^{[ нужна страница ]}

[11] Колб, Уильям М. (1984). Аппроксимация кривой для программируемых калькуляторов . СИНТЕК. ISBN 978-0-943494-02-9 . ^{[ нужна страница ]}

[12] Халли, СС; Рао, К.В. (1992). Передовые методы демографического анализа . Springer Science & Business Media. п. 165. ИСБН 978-0-306-43997-1 . Функции выполняются, если у нас есть хорошее или умеренное соответствие наблюдаемым данным.

[13] Сигнал и шум : почему так много прогнозов не работают, а некоторые нет. Нейт Сильвер

[14] Пайл, Дориан (1999). Подготовка данных для интеллектуального анализа данных . Морган Кауфманн. ISBN 978-1-55860-529-9 . ^{[ нужна страница ]}

[15] Численные методы в инженерии с MATLAB®. Автор Яан Киусалас . Страница 24.

[16] Киусалас, Яан (2013). Численные методы в проектировании с использованием Python 3 . Издательство Кембриджского университета. п. 21. ISBN 978-1-139-62058-1 .

[17] Гость, Филип Джордж (2012). Численные методы аппроксимации кривой . Издательство Кембриджского университета. п. 349. ИСБН 978-1-107-64695-7 .

[18] См. Также: Моллифер

[19] Мотульский, Харви; Христопулос, Артур (2004). Подгонка моделей к биологическим данным с использованием линейной и нелинейной регрессии: практическое руководство по подгонке кривой . Издательство Оксфордского университета. ISBN 978-0-19-803834-4 . ^{[ нужна страница ]}

[20] Регрессионный анализ Рудольфа Дж. Фройнда, Уильяма Дж. Уилсона, Ping Sa. Страница 269. ^{[ дата отсутствует ]}

[21] Дауд, Ханита; Сагаян, Виджант; Яхья, Нурхана; Наджвати, Ван (2009). «Моделирование электромагнитных волн с использованием статистических и численных методов». Визуальная информатика: соединение исследований и практики . Конспекты лекций по информатике. Том. 5857. стр. 686–695. дои : 10.1007/978-3-642-05036-7_65 . ISBN 978-3-642-05035-0 .

[22] Хаузер, Джон Р. (2009). Численные методы для нелинейных инженерных моделей . Springer Science & Business Media. п. 227. ИСБН 978-1-4020-9920-5 .

[23] Уильям, Дадли, изд. (1976). «Ядерная и атомная спектроскопия». Спектроскопия . Методы экспериментальной физики. Том. 13. С. 115–346 [150]. дои : 10.1016/S0076-695X(08)60643-2 . ISBN 978-0-12-475913-8 .

[24] Салкинд, Нил Дж. (2010). Энциклопедия дизайна исследований . МУДРЕЦ. п. 266. ИСБН 978-1-4129-6127-1 .

[25] Клостерман, Ричард Э. (1990). Методы анализа и планирования сообщества . Издательство Rowman & Littlefield. п. 1. ISBN 978-0-7425-7440-3 .

[26] Йо, Чарльз Э. (март 1996 г.). Введение в риск и неопределенность в оценке экологических инвестиций (Отчет). Инженерный корпус армии США. п. 69. ДТИК АДА316839 .

[27] Хэмминг, Ричард (2012). Численные методы для ученых и инженеров . Курьерская корпорация. ISBN 978-0-486-13482-6 . ^{[ нужна страница ]}

[28] Фридман, Милтон (декабрь 1962 г.). «Интерполяция временных рядов связанными рядами». Журнал Американской статистической ассоциации . 57 (300): 729–757. дои : 10.1080/01621459.1962.10500812 .

[29] Ганди, Сораб; Фоскини, Лука; Сури, Субхаш (2010). «Экономичное онлайн-аппроксимирование данных временных рядов: потоки, амнезия и нарушение порядка». 2010 26-я Международная конференция IEEE по инженерии данных (ICDE 2010) . стр. 924–935. дои : 10.1109/ICDE.2010.5447930 . ISBN 978-1-4244-5445-7 . S2CID 16072352 .

[30] Сэнди Риза (18 марта 2020 г.). «Анализ временных рядов с помощью Spark» (слайды доклада на Spark Summit East 2016) . Блоки данных . Проверено 12 января 2021 г.

[31] Золхавари, Сейеджамаль; Агабозорги, Саид; Тэ, Ин Ва (2014). «Обзор кластеризации временных рядов подпоследовательностей» . Научный мировой журнал . 2014 : 312521. дои : 10.1155/2014/312521 . ПМК 4130317 . ПМИД 25140332 .

[32] Кио, Имонн; Лин, Джессика (август 2005 г.). «Кластеризация подпоследовательностей временных рядов бессмысленна: последствия для предыдущих и будущих исследований». Знания и информационные системы . 8 (2): 154–177. дои : 10.1007/s10115-004-0172-7 .

[linear_time_series-33] Гершенфельд, Н. (1999). Природа математического моделирования . Нью-Йорк: Издательство Кембриджского университета. стр. 205–208 . ISBN 978-0521570954 .

[34] Канц, Хольгер; Томас, Шрайбер (2004). Нелинейный анализ временных рядов . Лондон: Издательство Кембриджского университета. ISBN 978-0521529020 .

[35] Абарбанель, Генри (25 ноября 1997 г.). Анализ наблюдаемых хаотических данных . Нью-Йорк: Спрингер. ISBN 978-0387983721 .

[36] Боашаш, Б. (редактор), (2003) Частотно-временной анализ и обработка сигналов: полный справочник , Elsevier Science, Оксфорд, 2003. ISBN 0-08-044335-4

[Nikolicetal-37] Николич, Данко; Мурешан, Рауль К.; Фэн, Вэйцзя; Певец Вольф (март 2012 г.). «Масштабный корреляционный анализ: лучший способ вычисления кросс-коррелограммы». Европейский журнал неврологии . 35 (5): 742–762. дои : 10.1111/j.1460-9568.2011.07987.x . ПМИД 22324876 . S2CID 4694570 .

[Sakoe_1978-38] Перейти обратно: ^а ^б Сакоэ, Х.; Чиба, С. (февраль 1978 г.). «Оптимизация алгоритма динамического программирования для распознавания устной речи». Транзакции IEEE по акустике, речи и обработке сигналов . 26 (1): 43–49. дои : 10.1109/ТАССП.1978.1163055 . S2CID 17900407 .

[39] Морманн, Флориан; Анджейак, Ральф Г.; Элджер, Кристиан Э.; Ленертц, Клаус (2007). «Прогнозирование приступов: долгий и извилистый путь» . Мозг . 130 (2): 314–333. дои : 10.1093/brain/awl241 . ПМИД 17008335 .

[40] Лэнд, Брюс; Элиас, Дамиан. «Измерение сложности временного ряда» .

[41] Чевырев Илья; Кормилицин, Андрей (2016). «Букварь по методу сигнатур в машинном обучении». arXiv : 1603.03788 .

[42] Ропелла, GEP; Наг, Д.А.; Хант, Калифорния (2003). «Меры сходства для автоматического сравнения результатов экспериментов in silico и in vitro». Материалы 25-й ежегодной международной конференции Общества инженеров в медицине и биологии IEEE (номер по каталогу IEEE 03CH37439) . стр. 2933–2936. дои : 10.1109/IEMBS.2003.1280532 . ISBN 978-0-7803-7789-9 . S2CID 17798157 .

[43] Томински, Кристиан; Айгнер, Вольфганг. «Браузер TimeViz: визуальный обзор методов визуализации данных, ориентированных на время» . Проверено 1 июня 2014 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]