Нечеткая логика

Эта статья о научной теории этого имени. Чтобы узнать о других значениях, см. Нечеткую логику (значения) .

Нечеткая логика — это форма многозначной логики, в которой истинное значение переменных может быть любым действительным числом от 0 до 1. Она используется для обработки концепции частичной истины, где значение истинности может варьироваться от полностью истинного до полностью ложного. . Напротив, в булевой логике истинностные значения переменных могут быть только целочисленными значениями 0 или 1.

Термин «нечеткая логика» предложил теорию нечетких множеств был введен в 1965 году, когда математик Лотфи Заде . Однако нечеткая логика изучалась с 1920-х годов как бесконечнозначная логика, особенно Лукасевичем и Тарским .

Нечеткая логика основана на наблюдении, что люди принимают решения на основе неточной и нечисловой информации. Нечеткие модели или нечеткие множества — это математические средства представления неопределенности и неточной информации (отсюда и термин «нечеткие»). Эти модели способны распознавать, представлять, манипулировать, интерпретировать и использовать расплывчатые и неопределенные данные и информацию.

Нечеткая логика применяется во многих областях, от теории управления до искусственного интеллекта .

Обзор

Классическая логика допускает только выводы, которые либо истинны, либо ложны. Однако существуют также предложения с переменными ответами, которые можно обнаружить, если попросить группу людей определить цвет. В таких случаях истина появляется в результате рассуждений, основанных на неточных или частичных знаниях, в которых выборочные ответы отображаются в спектре.

И степени истины и вероятности варьируются от 0 до 1 и, следовательно, на первый взгляд могут показаться одинаковыми, но нечеткая логика использует степени истины как математическую модель неопределенности , , тогда как вероятность — это математическая модель незнания .

Применение значений истинности

Базовое приложение может характеризовать различные поддиапазоны непрерывной переменной . Например, измерение температуры антиблокировочной системы тормозов может иметь несколько отдельных функций принадлежности, определяющих конкретные диапазоны температур, необходимые для правильного управления тормозами. Каждая функция сопоставляет одно и то же значение температуры со значением истинности в диапазоне от 0 до 1. Эти значения истинности затем можно использовать для определения того, как следует управлять тормозами. Теория нечетких множеств предоставляет средства представления неопределенности.

Лингвистические переменные

В приложениях нечеткой логики нечисловые значения часто используются для облегчения выражения правил и фактов.

Лингвистическая переменная, такая как возраст, может принимать такие значения, как молодой и его антоним старый . Поскольку естественные языки не всегда содержат достаточное количество значений, чтобы выразить нечеткую шкалу значений, общепринятой практикой является модификация лингвистических значений с помощью прилагательных или наречий . Например, мы можем использовать хеджирование скорее и в некоторой степени для создания дополнительных ценностей, довольно старых или несколько молодых .

Нечеткие системы

Мамдани

Наиболее известной системой является Мамдани . система, основанная на правилах Он использует следующие правила:

1. Фаззифицируйте все входные значения в нечеткие функции принадлежности.
2. Выполните все применимые правила в базе правил для вычисления нечетких выходных функций.
3. Дефаззифицируйте нечеткие выходные функции, чтобы получить «четкие» выходные значения.

Фаззификация

Фаззификация — это процесс присвоения числовых входных данных системы нечетким множествам с некоторой степенью членства. Эта степень членства может находиться где угодно в интервале [0,1]. Если это 0, то значение не принадлежит данному нечеткому множеству, а если оно равно 1, то значение полностью принадлежит нечеткому множеству. Любое значение от 0 до 1 представляет степень неопределенности принадлежности значения множеству. Эти нечеткие множества обычно описываются словами, и поэтому, назначая входные данные системы нечетким множествам, мы можем рассуждать с ними лингвистически естественным образом.

Например, на изображении ниже значения выражений «холодный» , «теплый » и «горячий» представлены функциями, отображающими температурную шкалу. Точка на этой шкале имеет три «истинных значения» — по одному для каждой из трех функций. Вертикальная линия на изображении представляет собой определенную температуру, которую измеряют три стрелки (истинные значения). Поскольку красная стрелка указывает на ноль, эту температуру можно интерпретировать как «негорячую»; т.е. эта температура не принадлежит к нечеткому множеству «горячие». Оранжевая стрелка (указывающая на 0,2) может описывать его как «слегка теплый», а синяя стрелка (указывающая на 0,8) — «довольно холодный». Следовательно, эта температура имеет 0,2 членства в нечетком множестве «теплый» и 0,8 членства в нечетком множестве «холодный». Степень принадлежности, присвоенная каждому нечеткому множеству, является результатом фаззификации.

Температура нечеткой логики

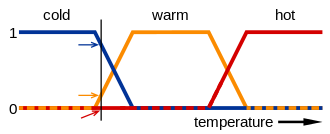
Нечеткие множества часто определяются как кривые в форме треугольника или трапеции, поскольку каждое значение будет иметь наклон, при котором значение увеличивается, пик, при котором значение равно 1 (который может иметь длину 0 или больше), и наклон, при котором значение увеличивается. ценность снижается. Их также можно определить с помощью сигмовидной функции . Одним из распространенных случаев является стандартная логистическая функция, определяемая как

$S(x)={\frac {1}{1+e^{-x}}}$,

который обладает следующим свойством симметрии

$$S(x)+S(-x)=1.$$

Отсюда следует, что

$$(S(x)+S(-x))\cdot (S(y)+S(-y))\cdot (S(z)+S(-z))=1$$

Операторы нечеткой логики

Нечеткая логика работает со значениями членства таким образом, что имитирует булевую логику . Для этого должны быть доступны замены базовым операторам AND, OR, NOT. Для этого есть несколько способов. Обычная замена называется Оператор Заде :

логическое значение	Нечеткий
И(х,у)	МИН(х,у)
ИЛИ(х,у)	МАКС(х,у)
НЕ(х)	1 – х

Для TRUE/1 и FALSE/0 нечеткие выражения дают тот же результат, что и логические выражения.

Существуют и другие операторы, более лингвистические по своей природе, называемые хеджами , которые можно применять. Обычно это наречия, такие как «очень » или «несколько », которые изменяют значение набора с помощью математической формулы .

Однако таблица произвольного выбора не всегда определяет функцию нечеткой логики. В статье (Зайцев и др.) Сформулирован критерий определения того, определяет ли данная таблица выбора функцию нечеткой логики, и предложен простой алгоритм синтеза функции нечеткой логики, основанный на введенных понятиях составляющих минимума и максимума. Функция нечеткой логики представляет собой дизъюнкцию составляющих минимума, где составляющая минимума представляет собой конъюнкцию переменных текущей области, больших или равных значению функции в этой области (справа от значения функции в неравенстве, в том числе значение функции).

Другой набор операторов И/ИЛИ основан на умножении, где

x AND y = x*y
NOT x = 1 - x

Hence, 
x OR y = NOT( AND( NOT(x), NOT(y) ) )
x OR y = NOT( AND(1-x, 1-y) )
x OR y = NOT( (1-x)*(1-y) )
x OR y = 1-(1-x)*(1-y)
x OR y = x+y-xy

Учитывая любые два из И/ИЛИ/НЕ, можно получить третье. Обобщение AND является примером t-нормы .

Правила ЕСЛИ-ТО

Основная статья: Нечеткое правило

Правила IF-THEN сопоставляют входные или вычисленные значения истинности с желаемыми выходными значениями истинности. Пример:

IF temperature IS very cold THEN fan_speed is stopped
IF temperature IS cold THEN fan_speed is slow
IF temperature IS warm THEN fan_speed is moderate
IF temperature IS hot THEN fan_speed is high

При определенной температуре нечеткая переменная hot имеет определенное значение истинности, которое копируется в переменную high .

Если выходная переменная встречается в нескольких частях THEN, то значения из соответствующих частей IF объединяются с помощью оператора OR.

Дефаззификация

Основная статья: Дефаззификация

Цель состоит в том, чтобы получить непрерывную переменную из нечетких значений истинности.

Это было бы легко, если бы выходные значения истинности были в точности теми, которые получены в результате фаззификации заданного числа. Однако поскольку все выходные значения истинности вычисляются независимо, в большинстве случаев они не представляют собой такой набор чисел. Затем нужно выбрать число, которое лучше всего соответствует «намерению», закодированному в значении истинности. Например, для нескольких значений истинности fan_speed необходимо найти фактическую скорость, которая лучше всего соответствует вычисленным значениям истинности переменных «медленный», «умеренный» и т. д.

Единого алгоритма для этой цели не существует.

Общий алгоритм:

1. Для каждого значения истинности обрежьте функцию принадлежности по этому значению.
2. Объедините полученные кривые с помощью оператора ИЛИ
3. Найдите центр тяжести площади под кривой.
4. Положение x этого центра является окончательным результатом.

Такаги-Сугено-Канг (TSK)

Система ТСК аналогичен Мамдани, но процесс дефаззификации включен в выполнение нечетких правил. Они также адаптированы так, что вместо этого результат правила представляется через полиномиальную функцию (обычно постоянную или линейную). Примером правила с постоянным выходом может быть:

IF temperature IS very cold = 2

В этом случае выход будет равен константе консеквента (например, 2). В большинстве сценариев у нас будет вся база правил с двумя или более правилами. В этом случае выходные данные всей базы правил будут представлять собой среднее значение консеквента каждого правила i (Y _i ), взвешенного в соответствии со значением членства его антецедента (hi ₎ :

${\frac {\sum _{i}(h_{i}\cdot Y_{i})}{\sum _{i}h_{i}}}$

Вместо этого примером правила с линейным выходом будет:

IF temperature IS very cold AND humidity IS high = 2 * temperature +  1 * humidity

В этом случае вывод правила будет результатом функции в консеквенте. Переменные внутри функции представляют значения членства после фаззификации, а не четкие значения. Как и раньше, если у нас есть вся база правил с двумя или более правилами, общий результат будет представлять собой средневзвешенное значение между результатами каждого правила.

Основное преимущество использования TSK перед Mamdani заключается в том, что оно эффективно в вычислительном отношении и хорошо работает с другими алгоритмами, такими как ПИД-управление, и с алгоритмами оптимизации. Это также может гарантировать непрерывность выходной поверхности. Однако Мамдани более интуитивен, и с ним легче работать. Следовательно, TSK обычно используется в других сложных методах, например, в адаптивных системах нейронечеткого вывода .

Формирование консенсуса исходных данных и нечетких правил

Поскольку выходные данные нечеткой системы представляют собой консенсус всех входных данных и всех правил, системы нечеткой логики могут вести себя хорошо, когда входные значения недоступны или не заслуживают доверия. К каждому правилу в базе правил можно дополнительно добавить веса, а также использовать их для регулирования степени влияния правила на выходные значения. Эти веса правил могут основываться на приоритете, надежности или последовательности каждого правила. Эти веса правил могут быть статическими или изменяться динамически, даже на основе результатов других правил.

Приложения

Нечеткая логика используется в системах управления , чтобы позволить экспертам вводить расплывчатые правила, такие как «если вы находитесь близко к станции назначения и двигаетесь быстро, увеличьте тормозное давление поезда»; эти расплывчатые правила затем могут быть уточнены численно внутри системы.

Многие из первых успешных применений нечеткой логики были реализованы в Японии. Первое заметное применение было в серии Sendai Subway 1000 , в которой нечеткая логика смогла улучшить экономичность, комфорт и точность поездки. Он также использовался для распознавания рукописного текста в карманных компьютерах Sony, средствах управления полетом на вертолетах, средствах управления системой метро, ​​повышения топливной экономичности автомобилей, однокнопочном управлении стиральными машинами, автоматическом управлении мощностью в пылесосах и раннем распознавании землетрясений в Институте сейсмологии. Бюро метеорологии, Япония.

Искусственный интеллект

Основная статья: Нейро-нечеткий

нейронных сетях , основанный на Искусственный интеллект , и нечеткая логика при анализе представляют собой одно и то же: основная логика нейронных сетей является нечеткой. Нейронная сеть будет принимать различные ценные входные данные, придавать им разные веса по отношению друг к другу, объединять промежуточные значения определенное количество раз и принимать решение с определенным значением. Нигде в этом процессе нет ничего похожего на последовательность решений «или-или», которая характеризует нечеткую математику, компьютерное программирование и цифровую электронику . В 1980-х годах мнения исследователей разделились во мнениях относительно наиболее эффективного подхода к машинному обучению : обучение дереву решений или нейронные сети. Первый подход использует двоичную логику, соответствующую оборудованию, на котором он работает, но, несмотря на большие усилия, он не привел к созданию интеллектуальных систем. Нейронные сети, напротив, позволили создать точные модели сложных ситуаций и вскоре нашли применение во множестве электронных устройств. Теперь их также можно реализовать непосредственно на аналоговых микрочипах, в отличие от предыдущих псевдоаналоговых реализаций на цифровых чипах. Более высокая эффективность компенсирует присущую аналогу меньшую точность в различных случаях использования.

медицинских

Нечеткая логика является важной концепцией при принятии медицинских решений . Поскольку медицинские и медицинские данные могут быть субъективными или нечеткими, приложения в этой области имеют большой потенциал, чтобы получить большую выгоду от использования подходов, основанных на нечеткой логике.

Нечеткая логика может использоваться во многих различных аспектах процесса принятия медицинских решений. К таким аспектам относятся в анализе медицинских изображений , анализе биомедицинских сигналов, сегментации изображений или сигналов, а также извлечение признаков /выбор изображений или сигналы.

Самый большой вопрос в этой области приложений заключается в том, сколько полезной информации можно получить при использовании нечеткой логики. Основная проблема заключается в том, как получить необходимые нечеткие данные. Это становится еще более сложной задачей, когда приходится получать такие данные от людей (обычно пациентов). Как было сказано

«По иронии судьбы, границы того, чего можно достичь и чего нельзя достичь в медицинской диагностике, сами по себе нечеткие»

— Семь вызовов, 2019.

Как получить нечеткие данные и как проверить точность данных, все еще остается предметом постоянной работы, тесно связанной с применением нечеткой логики. Проблема оценки качества нечетких данных является сложной. Вот почему нечеткая логика является весьма многообещающей возможностью в области применения принятия медицинских решений, но для полной реализации ее потенциала все еще требуются дополнительные исследования. Хотя концепция использования нечеткой логики в принятии медицинских решений является захватывающей, все еще существует несколько проблем, с которыми сталкиваются нечеткие подходы в рамках процесса принятия медицинских решений.

Компьютерная диагностика

Одной из распространенных областей применения нечеткой логики является компьютерная диагностика на основе изображений в медицине. Компьютерная диагностика — это компьютеризированный набор взаимосвязанных инструментов, которые можно использовать, чтобы помочь врачам в принятии диагностических решений. Например, когда врач обнаруживает поражение, которое является аномальным, но все еще находится на очень ранней стадии развития, он/она может использовать компьютерную диагностику, чтобы охарактеризовать поражение и диагностировать его природу. Нечеткая логика может быть весьма подходящей для описания ключевых характеристик этого поражения.

Нечеткие базы данных

После определения нечетких отношений можно разрабатывать нечеткие реляционные базы данных . Первая нечеткая реляционная база данных FRDB появилась в Марии Земанковой диссертации (1983). Позже возникли некоторые другие модели, такие как модель Баклса-Петри, модель Праде-Тестемале, модель Умано-Фуками или модель GEFRED Дж. М. Медины, М. А. Вила и др.

Были определены языки нечетких запросов, такие как SQLf П. Боска и др. и FSQL Дж. Галиндо и др. Эти языки определяют некоторые структуры для включения нечетких аспектов в операторы SQL, таких как нечеткие условия, нечеткие компараторы, нечеткие константы, нечеткие ограничения, нечеткие пороги, лингвистические метки и т. д.

Логический анализ

В математической логике существует несколько формальных систем «нечеткой логики», большинство из которых относятся к семейству нечетких логик t-нормы .

Пропозициональная нечеткая логика

Наиболее важными пропозициональными нечеткими логиками являются:

• Моноидальная пропозициональная нечеткая логика, основанная на t-норме, MTL представляет собой аксиоматизацию логики, в которой соединение определяется непрерывной слева t-нормой , а импликация определяется как остаток t-нормы. Ее модели соответствуют MTL-алгебрам, представляющим собой предлинейные коммутативные ограниченные целочисленные вычетные решетки .
• Базовая пропозициональная нечеткая логика BL является расширением логики MTL, где конъюнкция определяется непрерывной t-нормой, а импликация также определяется как остаток t-нормы. Ее модели соответствуют BL-алгебрам.
• Нечеткая логика Лукасевича является расширением базовой нечеткой логики BL, где стандартным соединением является t-норма Лукасевича. Он имеет аксиомы базовой нечеткой логики плюс аксиому двойного отрицания, а его модели соответствуют MV-алгебрам .
• Нечеткая логика Гёделя является расширением базовой нечеткой логики BL, где конъюнкция является t-нормой Гёделя (то есть минимумом). Она имеет аксиомы BL плюс аксиому идемпотентности конъюнкции, а ее модели называются G-алгебрами.
• Нечеткая логика продукта является расширением базовой нечеткой логики BL, где соединение является t-нормой продукта. Он имеет аксиомы BL плюс еще одну аксиому об отмене конъюнкции, а его модели называются алгебрами произведений.
• Нечеткая логика с вычисляемым синтаксисом (иногда также называемая логикой Павельки), обозначаемая EVŁ, представляет собой дальнейшее обобщение математической нечеткой логики. Хотя вышеупомянутые виды нечеткой логики имеют традиционный синтаксис и многозначную семантику, в EVŁ также оценивается синтаксис. Это означает, что каждая формула имеет оценку. Аксиоматизация EVŁ происходит из нечеткой логики Лукасевича. Обобщение классической теоремы Гёделя о полноте доказуемо в EVŁ. .

логика

Подобно тому, как логика предикатов создается из логики высказываний , нечеткая логика предикатов расширяет нечеткие системы с помощью универсальных и экзистенциальных кванторов . Семантика квантора универсальности в нечеткой логике t-нормы является нижней границей степеней истинности экземпляров кванторной подформулы, тогда как семантика квантора существования является верхней границей ее .

Проблемы

Понятия «разрешимое подмножество» и « рекурсивно перечислимое подмножество» являются базовыми для классической математики и классической логики . Таким образом, вопрос о подходящем их расширении до теории нечетких множеств является решающим. Первое предложение в таком направлении было сделано Э.С. Сантосом с помощью понятий нечеткой машины Тьюринга , нормального нечеткого алгоритма Маркова и нечеткой программы (см. Сантос 1970). Последовательно Л. Бьячино и Г. Герла утверждали, что предложенные определения весьма сомнительны. Например, в один показывает, что нечеткие машины Тьюринга не подходят для теории нечетких языков, поскольку существуют естественные нечеткие языки, интуитивно вычислимые, которые не могут быть распознаны нечеткой машиной Тьюринга. Тогда они предложили следующие определения. Обозначим через Ü множество рациональных чисел из [0,1]. Тогда нечеткое подмножество s : S $\rightarrow$ [0,1] множества S рекурсивно перечислимо, если рекурсивное отображение h : S × N $\rightarrow$Ü существует такое, что для каждого x в S функция h ( x , n ) возрастает по отношению к n и s ( x ) = lim h ( x , n ). Мы говорим, что s разрешимо , если и s , и его дополнение – s рекурсивно перечислимы. Возможно распространение такой теории на общий случай L-подмножеств (см. Gerla 2006). Предложенные определения хорошо связаны с нечеткой логикой. Действительно, справедлива следующая теорема (при условии, что аппарат вывода рассматриваемой нечеткой логики удовлетворяет некоторому очевидному свойству эффективности).

Любая «аксиоматизируемая» нечеткая теория рекурсивно перечислима. В частности, нечеткое множество логически истинных формул является рекурсивно перечислимым, несмотря на то, что четкое множество действительных формул вообще не является рекурсивно перечислимым. Более того, любая аксиоматизируемая и полная теория разрешима.

Вопрос о поддержке «тезиса Чёрча» для нечеткой математики остается открытым , предлагаемое понятие рекурсивной перечислимости для нечетких подмножеств является адекватным. расширение понятий нечеткой грамматики и нечеткой машины Тьюринга Чтобы решить эту проблему, необходимо . Другой открытый вопрос — начать с этого понятия, чтобы найти распространение теорем Гёделя на нечеткую логику.

По сравнению с другими логиками

Вероятность

Нечеткая логика и вероятность касаются различных форм неопределенности. Хотя и нечеткая логика, и теория вероятностей могут отражать степени определенных видов субъективных убеждений, теория нечетких множеств использует концепцию принадлежности к нечеткому множеству, т. е. того, насколько наблюдение находится в пределах неопределенно определенного множества, а теория вероятностей использует концепцию субъективной вероятности. , то есть частота возникновения или вероятность какого-либо события или условия . Концепция нечетких множеств была разработана в середине двадцатого века в Беркли. как ответ на отсутствие теории вероятностей для совместного моделирования неопределенности и неопределенности .

Барт Коско утверждает в книге «Нечеткость против вероятности» что теория вероятностей является подтеорией нечеткой логики, поскольку вопросы степени веры во взаимоисключающее членство во множестве в теории вероятностей могут быть представлены как определенные случаи невзаимоисключающего градуированного членства в нечеткой теории. В этом контексте он также выводит теорему Байеса из концепции нечеткого подмножества. Лотфи А. Заде утверждает, что нечеткая логика по своему характеру отличается от вероятности и не является ее заменой. Он превратил вероятность в нечеткую вероятность, а также обобщил ее на теорию возможностей .

В более общем смысле, нечеткая логика — это одно из многих различных расширений классической логики, предназначенное для решения проблем неопределенности, выходящих за рамки классической логики, неприменимости теории вероятностей во многих областях и парадоксов теории Демпстера-Шейфера .

Экорифмы

Теоретик вычислений Лесли Валиант использует термин «экорифмы» для описания того, сколько менее точных систем и методов, таких как нечеткая логика (и «менее робастная» логика), можно применить к алгоритмам обучения . Valiant по сути переопределяет машинное обучение как эволюционное. В общем случае экорифмы — это алгоритмы, которые учатся на более сложной среде (следовательно, эко- ) обобщать, аппроксимировать и упрощать логику решения. Подобно нечеткой логике, они представляют собой методы, используемые для преодоления непрерывных переменных или систем, слишком сложных, чтобы их можно было полностью перечислить или понять дискретно или точно. Экоритмы и нечеткая логика также имеют общее свойство иметь дело с возможностями, а не с вероятностями, хотя обратная связь и прямая связь , по сути, стохастические веса, являются особенностью обоих, когда речь идет, например, о динамических системах .

Гёдель G _∞ логика

Дополнительная информация: Многозначная логика § Логики Гёделя Gk и G∞.

Другая логическая система, в которой истинностные значения представляют собой действительные числа от 0 до 1 и где операторы И и ИЛИ заменены на MIN и MAX, — это _{G ∞} логика Гёделя. Эта логика имеет много общего с нечеткой логикой, но по-другому определяет отрицание и имеет внутренний смысл. Отрицание $\neg _{G}$ и последствия ${\xrightarrow[{G}]{}}$ определяются следующим образом:

${\begin{aligned}\neg _{G}u&={\begin{cases}1,&{\text{if }}u=0\\0,&{\text{if }}u>0\end{cases}}\\[3pt]u\mathrel {\xrightarrow[{G}]{}} v&={\begin{cases}1,&{\text{if }}u\leq v\\v,&{\text{if }}u>v\end{cases}}\end{aligned}}$

который превращает результирующую логическую систему в модель интуиционистской логики , делая ее особенно хорошей среди всех возможных вариантов логических систем с действительными числами от 0 до 1 в качестве значений истинности. В этом случае импликацию можно интерпретировать как «x менее истинно, чем y», а отрицание — как «x менее истинно, чем 0» или «x строго ложно», и для любого $x$ и $y$, у нас это есть $AND(x,x\mathrel {\xrightarrow[{G}]{}} y)=AND(x,y)$. В частности, в логике Гёделя отрицание больше не является инволюцией, а двойное отрицание отображает любое ненулевое значение в 1.

логика

Компенсаторная нечеткая логика (КФЛ) — это ветвь нечеткой логики с модифицированными правилами конъюнкции и дизъюнкции. Когда значение истинности одного компонента соединения или дизъюнкции увеличивается или уменьшается, другой компонент уменьшается или увеличивается для компенсации. Это увеличение или уменьшение значения истинности может быть компенсировано увеличением или уменьшением другого компонента. Смещение может быть заблокировано при достижении определенных пороговых значений. Сторонники утверждают, что CFL позволяет улучшить вычислительное семантическое поведение и имитировать естественный язык.

По словам Хесуса Сехаса Монтеро (2011), компенсаторная нечеткая логика состоит из четырех непрерывных операторов: конъюнкции (c); дизъюнкция (г); нечеткий строгий порядок (или); и отрицание (н). Конъюнкция — это среднее геометрическое и двойственные ей операторы — конъюнктивный и дизъюнктивный.

Стандартизация языка разметки

IEEE 1855 , СТАНДАРТ IEEE 1855–2016, посвящен языку спецификации под названием Fuzzy Markup Language (FML). разработан Ассоциацией стандартов IEEE . FML позволяет моделировать систему нечеткой логики понятным для человека и независимым от оборудования способом. FML основан на расширяемом языке разметки ( XML ). Разработчики нечетких систем с помощью FML имеют унифицированную методологию высокого уровня для описания совместимых нечетких систем. СТАНДАРТ IEEE 1855–2016 использует W3C язык определения схемы XML для определения синтаксиса и семантики программ FML.

До появления FML специалисты по нечеткой логике могли обмениваться информацией о своих нечетких алгоритмах, добавляя к функциям своего программного обеспечения возможность читать, правильно анализировать и сохранять результаты своей работы в форме, совместимой с языком нечеткого управления (FCL). описано и определено в части 7 стандарта IEC 61131 .

См. также

• Адаптивная система нейронечеткого вывода (ANFIS)
• Искусственная нейронная сеть
• Байесовский вывод
• Дефаззификация
• Экспертная система
• Ложная дилемма
• Нечеткий архитектурно-пространственный анализ
• Нечеткая классификация
• Нечеткая концепция
• Язык нечеткого управления
• Нечеткая система управления
• Нечеткая электроника
• Нечеткая подалгебра
• FuzzyCLIPS
• Высокопроизводительные нечеткие вычисления
• Транзакции IEEE в нечетких системах
• Интервальный конечный элемент
• Машинное обучение
• Нейро-нечеткий
• Логика, основанная на шуме
• Грубый набор
• Парадокс Сорита
• Троичная логика
• Нечеткие множества и системы типа 2
• Векторная логика

Библиография

• Арабачиоглу, Британская Колумбия (2010). «Использование системы нечеткого вывода для анализа архитектурного пространства». Прикладные мягкие вычисления . 10 (3): 926–937. дои : 10.1016/j.asoc.2009.10.011 .
• Бьячино, Лоредана; Герла, Джанджакомо (1 октября 2002 г.). «Нечеткая логика, непрерывность и эффективность». Архив математической логики . 41 (7): 643–667. CiteSeerX   10.1.1.2.8029 . дои : 10.1007/s001530100128 . S2CID   12513452 .
• Кокс, Эрл (1994). Справочник по нечетким системам: руководство для практикующего специалиста по созданию, использованию и обслуживанию нечетких систем . Бостон: AP Professional. ISBN  978-0-12-194270-0 .
• Герла, Джанджакомо (март 2006 г.). «Эффективность и многозначная логика». Журнал символической логики . 71 (1): 137–162. дои : 10.2178/jsl/1140641166 . S2CID   12322009 .
• Гаек, Петр (1998). Метаматематика нечеткой логики . Дордрехт: Клювер. ISBN  978-0-7923-5238-9 .
• Гаек, Петр (август 1995 г.). «Нечеткая логика и арифметическая иерархия». Нечеткие множества и системы . 73 (3): 359–363. дои : 10.1016/0165-0114(94)00299-М .
• Халперн, Джозеф Ю. (2003). Рассуждения о неопределенности . Кембридж, Массачусетс: MIT Press . ISBN  978-0-262-08320-1 .
• Хеппнер, Франк; Клавонн, Ф.; Крузе, Р. ; Ранклер, Т. (1999). Нечеткий кластерный анализ: методы классификации, анализа данных и распознавания изображений . Нью-Йорк: Джон Уайли. ISBN  978-0-471-98864-9 .
• Ибрагим, Ахмад М. (1997). Введение в прикладную нечеткую электронику . Энглвуд Клиффс, Нью-Джерси: Прентис Холл . ISBN  978-0-13-206400-2 .
• Клир, Георгий Иржи ; Фолджер, Тина А. (1988). Нечеткие множества, неопределенность и информация . Энглвуд Клиффс, Нью-Джерси: Прентис Холл . ISBN  978-0-13-345984-5 .
• Клир, Георгий Иржи ; Сент-Клер, Ют Х.; Юань, Бо (1997). Теория нечетких множеств: основы и приложения . Энглвуд Клиффс, Нью-Джерси: Прентис Холл . ISBN  978-0-13-341058-7 .
• Клир, Георгий Иржи ; Юань, Бо (1995). Нечеткие множества и нечеткая логика: теория и приложения . Река Аппер-Сэддл, Нью-Джерси: PTR Prentice Hall . ISBN  978-0-13-101171-7 .
• Коско, Барт (1993). Нечеткое мышление: новая наука нечеткой логики . Нью-Йорк: Гиперион. ISBN  978-0-7868-8021-8 .
• Коско, Барт; Исака, Сатору (июль 1993 г.). «Нечеткая логика». Научный американец . 269 ​​(1): 76–81. Бибкод : 1993SciAm.269a..76K . doi : 10.1038/scientificamerican0793-76 .
• Лохани, АК; Гоэл, Северная Каролина; Бхатия, ККС (2006). «Система нечеткого вывода Такаги – Сугено для моделирования взаимосвязи между стадией и разрядом». Журнал гидрологии . 331 (1): 146–160. Бибкод : 2006JHyd..331..146L . doi : 10.1016/j.jгидрол.2006.05.007 .
• Лохани, АК; Гоэл, Северная Каролина; Бхатия, ККС (2007). «Вывод взаимосвязей стадия – расход – концентрация отложений с использованием нечеткой логики». Журнал гидрологических наук . 52 (4): 793–807. Бибкод : 2007HydSJ..52..793L . дои : 10.1623/hysj.52.4.793 . S2CID   117782707 .
• Лохани, АК; Гоэл, Северная Каролина; Бхатия, ККС (2012). «Моделирование гидрологических временных рядов: сравнение адаптивных нейро-нечетких методов, нейронных сетей и авторегрессионных методов». Журнал гидрологии . 442–443 (6): 23–35. Бибкод : 2012JHyd..442...23L . doi : 10.1016/j.j Hydrol.2012.03.031 .
• Масмуди, Малек; Хаит, Ален (ноябрь 2012 г.). «Моделирование нечеткой неопределенности для планирования проектов; применение к техническому обслуживанию вертолетов» (PDF) . Международный журнал производственных исследований . 50 (24). Архивировано (PDF) из оригинала 22 сентября 2017 года.
• Мериго, Хосе М.; Хиль-Лафуэнте, Анна М.; Ягер, Рональд Р. (февраль 2015 г.). «Обзор нечетких исследований с библиометрическими показателями». Прикладные мягкие вычисления . 27 : 420–433. дои : 10.1016/j.asoc.2014.10.035 .
• Миронов А.М. (август 2005 г.). «Нечеткая модальная логика» . Журнал математических наук . 128 (6): 3461–3483. дои : 10.1007/s10958-005-0281-1 . S2CID   120674564 .
• Монтанья, Франко (2001). «Три задачи сложности в количественной нечеткой логике». Студия Логика . 68 (1): 143–152. дои : 10.1023/А:1011958407631 . S2CID   20035297 .
• Мундичи, Даниэль; Чиньоли, Роберто; Д'Оттавиано, Итала МЛ (1999). Алгебраические основы многозначных рассуждений . Дордрехт: Клювер Академик. ISBN  978-0-7923-6009-4 .
• Новак, Вилем (1989). Нечеткие множества и их приложения . Бристоль: Адам Хильгер. ISBN  978-0-85274-583-0 .
• Новак, Вилем (2005). «О теории нечетких типов». Нечеткие множества и системы . 149 (2): 235–273. дои : 10.1016/j.fss.2004.03.027 .
• Новак, Вилем; Перфильева Ирина; Мочкорж, Иржи (1999). Математические принципы нечеткой логики . Дордрехт: Клювер Академик. ISBN  978-0-7923-8595-0 .
• Онсес, Ричард (1996). Экспертон второго порядка: новый инструмент для изменения парадигм расчета странового риска . Университет, Секретарь публикаций. ISBN  978-84-7719-558-0 .
• Онсес, Ричард (1994). Определение неопределенности, свойственной инвестициям в Латинской Америке, на основе теории нечетких подмножеств . Барселона. ISBN  978-84-475-0881-5 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Пассино, Кевин М.; Юркович, Стивен (1998). Нечеткое управление . Бостон: Аддисон-Уэсли . ISBN  978-0-201-18074-9 .
• Педрич, Витольд; Гомиде, Фернандо (2007). Инженерия нечетких систем: на пути к человекоцентричным вычислениям . Хобокен: Wiley-Interscience . ISBN  978-0-471-78857-7 .
• Пао-Мин, Пу ; Ин-Мин, Лю (август 1980 г.). «Нечеткая топология. I. Структура окрестности нечеткой точки и сходимость Мура-Смита» . Журнал математического анализа и приложений . 76 (2): 571–599. дои : 10.1016/0022-247X(80)90048-7 .
• Саху, Бхабаграхи; Лохани, АК; Саху, Рохит К. (2006). «Модели управления на основе нечеткого многокритериального и линейного программирования для оптимального планирования системы земля-вода-культуры». Управление водными ресурсами . 20 (6): 931–948. Бибкод : 2006WatRM..20..931S . дои : 10.1007/s11269-005-9015-x . S2CID   154264034 .
• Сантос, Юджин С. (1970). «Нечеткие алгоритмы» . Информация и контроль . 17 (4): 326–339. дои : 10.1016/S0019-9958(70)80032-8 .
• Скарпеллини, Бруно (июнь 1962 г.). «Неаксиоматизируемость бесконечнозначного исчисления предикатов Лукасевича». Журнал символической логики . 27 (2): 159–170. дои : 10.2307/2964111 . hdl : 20.500.11850/423097 . JSTOR   2964111 . S2CID   26330059 .
• Зейсинг, Рудольф (2007). Фаззификация систем. Генезис теории нечетких множеств и ее первоначальные применения – развитие до 1970-х годов . Спрингер-Верлаг. ISBN  978-3-540-71795-9 .
• Стееб, Вилли-Ханс (2008). Нелинейная рабочая тетрадь: хаос, фракталы, клеточные автоматы, нейронные сети, генетические алгоритмы, программирование экспрессии генов, машина опорных векторов, вейвлеты, скрытые марковские модели, нечеткая логика с программами на C ++, Java и Symbolic C ++ (4-е изд.). Всемирная научная. ISBN  978-981-281-852-2 .
• Цитоловский Лев; Сэндлер, Узиэль (2008). Поведение нейронных клеток и нечеткая логика . Спрингер. ISBN  978-0-387-09542-4 .
• Видерманн, Дж. (2004). «Охарактеризация супер-Тьюринговой вычислительной мощности и эффективности классических нечетких машин Тьюринга» . Теоретическая информатика . 317 (1–3): 61–69. дои : 10.1016/j.tcs.2003.12.004 .
• Ягер, Рональд Р.; Филев, Димитар П. (1994). Основы нечеткого моделирования и управления . Нью-Йорк: Уайли. ISBN  978-0-471-01761-5 .
• Ван Пелт, Майлз (2008). Нечеткая логика в применении к повседневной жизни . Сиэтл, Вашингтон: Нет Нет Нет Нет Пресса. ISBN  978-0-252-16341-8 .
• Фон Альтрок, Константин (1995). Объяснение нечеткой логики и приложений NeuroFuzzy . Река Аппер-Сэддл, Нью-Джерси: PTR Prentice Hall. ISBN  978-0-13-368465-0 .
• Уилкинсон, Р.Х. (1963). «Метод построения функций нескольких переменных с использованием аналоговой диодной логики». Транзакции IEEE на электронных компьютерах . 12 (2): 112–129. дои : 10.1109/PGEC.1963.263419 .
• Заде, Луизиана (февраль 1968 г.). «Нечеткие алгоритмы» . Информация и контроль . 12 (2): 94–102. дои : 10.1016/S0019-9958(68)90211-8 .
• Заде, Луизиана (июнь 1965 г.). «Нечеткие множества» . Информация и контроль . 8 (3). Сан-Диего: 338–353. дои : 10.1016/S0019-9958(65)90241-X . ISSN   0019-9958 . Збл   0139.24606 . Викиданные   Q25938993 .
• Зайцев Д.А.; Сарбей, В.Г.; Слепцов, А.И. (1998). «Синтез функций непрерывной логики, определенных в табличной форме». Кибернетика и системный анализ . 34 (2): 190–195. дои : 10.1007/BF02742068 . S2CID   120220846 .
• Циммерманн, Х. (2001). Теория нечетких множеств и ее приложения . Бостон: Kluwer Academic Publishers . ISBN  978-0-7923-7435-0 .

Внешние ссылки

• IEC 1131-7 CD1. Архивировано 4 марта 2021 г. на Wayback Machine. IEC 1131-7 CD1 PDF.
• Нечеткая логика - статья в Scholarpedia
• Моделирование с помощью слов - статья в Scholarpedia
• Нечеткая логика - статья в Стэнфордской энциклопедии философии
• Нечеткая математика – введение в нечеткую логику на начальном уровне.
• Нечеткость и точность . Нечеткость в повседневной жизни, науке, религии, этике, политике и т. д.
• Fuzzylite — кроссплатформенная бесплатная библиотека управления нечеткой логикой с открытым исходным кодом, написанная на C++. Также имеет очень полезный графический интерфейс пользователя в QT4.
• Более гибкое машинное обучение . MIT описывает одно приложение.
• Семантическое сходство. Архивировано 4 октября 2015 г. в Wayback Machine MIT. В нем содержится подробная информация о нечетком семантическом сходстве.