Т-норма

В математике t -норма (также T-норма или, несокращенно, треугольная норма ) — это разновидность бинарной операции, используемая в рамках вероятностных метрических пространств и в многозначной логике , в частности в нечеткой логике . Т-норма обобщает пересечение в решетке и конъюнкцию в логике . Название треугольная норма относится к тому факту, что в рамках вероятностных метрических пространств t-нормы используются для обобщения неравенства треугольника обычных метрических пространств .

Определение

t-норма — это функция T: [0, 1] × [0, 1] → [0, 1], которая удовлетворяет следующим свойствам:

Коммутативность : Т( а , б ) = Т( б , а )
Монотонность : T( a , b ) ≤ T( c , d ), если a ≤ c и b ≤ d
Ассоциативность : Т( а , Т( б , с )) = Т(Т( а , б ), с )
Число 1 действует как единичный элемент : T( a , 1) = a

Поскольку t-норма является бинарной алгебраической операцией на интервале [0, 1], также распространены инфиксные алгебраические обозначения, при этом t-норма обычно обозначается как $*$ .

Определяющие условия t-нормы в точности совпадают с условиями частично упорядоченного абелева моноида на вещественном единичном интервале [0, 1]. (См. упорядоченная группа .) Поэтому моноидальная операция любого частично упорядоченного абелева моноида L некоторыми авторами называется треугольной нормой на L .

Классификация Т-норм

t-норма называется непрерывной , если она непрерывна как функция в обычной интервальной топологии на [0, 1] ². (Аналогично для непрерывности слева и справа .)

t-норма называется строгой, если она непрерывна и строго монотонна .

t-норма называется нильпотентной, если она непрерывна и каждый x в открытом интервале (0, 1) нильпотентен , то есть существует натуральное число n такое, что x $*$ ... $*$ x ( n раз) равно 0.

Т-норма $*$ называется архимедовым, если оно обладает архимедовым свойством , то есть если для каждого x , y в открытом интервале (0, 1) существует натуральное число n такое, что x $*$ ... $*$ x ( n раз) меньше или равно y .

Обычное частичное упорядочение t-норм является точечным , т. е.

T ₁ ≤ T ₂ , если T ₁ ( a , b ) ≤ T ₂ ( a , b ) для всех a , b в [0, 1].

Как функции, поточечно большие t-нормы иногда называют более сильными, чем поточечно меньшие. Однако в семантике нечеткой логики, чем больше t-норма, тем более слабую (с точки зрения логической силы) конъюнкцию она представляет.

Яркие примеры

График минимальной t-нормы (3D и контуры)

Минимальная Т-норма $\top _{\mathrm {min} }(a,b)=\min\{a,b\},$ также называется t-нормой Гёделя , поскольку это стандартная семантика конъюнкции в нечеткой логике Гёделя . Кроме того, это встречается в большинстве нечетких логик, основанных на t-норме, как стандартная семантика для слабой конъюнкции. Это наибольшая поточечно t-норма (см. свойства t-норм ниже).

Т-норма продукта $\top _{\mathrm {prod} }(a,b)=a\cdot b$ (обычное произведение действительных чисел). Помимо других применений, t-норма продукта является стандартной семантикой для сильной конъюнкции в нечеткой логике продукта . Это строгая архимедова t-норма.

Лукасевич t-норма $\top _{\mathrm {Luk} }(a,b)=\max\{0,a+b-1\}.$ Название происходит от того факта, что t-норма является стандартной семантикой для сильной конъюнкции в нечеткой логике Лукасевича . Это нильпотентная архимедова t-норма, точечно меньшая, чем t-норма произведения.

График радикальной t-нормы. Функция разрывна на прямых 0 < x = 1 и 0 < y = 1.

Резкая Т-норма

\top _{\mathrm {D} }(a,b)={\begin{cases}b&{\mbox{if }}a=1\\a&{\mbox{if }}b=1\\0&{\mbox{otherwise.}}\end{cases}}

Название отражает тот факт, что резкая t-норма является наименьшей поточечно t-нормой (см. свойства t-норм ниже). Это непрерывная справа архимедова t-норма.

График нильпотентного минимума. Функция разрывна на прямой 0 < x = 1 − y < 1.

Нильпотентный минимум

\top _{\mathrm {nM} }(a,b)={\begin{cases}\min(a,b)&{\mbox{if }}a+b>1\\0&{\mbox{otherwise}}\end{cases}}

является стандартным примером t-нормы, непрерывной слева, но не непрерывной. Несмотря на свое название, нильпотентный минимум не является нильпотентной t-нормой.

Продукт Хамахер

\top _{\mathrm {H} _{0}}(a,b)={\begin{cases}0&{\mbox{if }}a=b=0\\{\frac {ab}{a+b-ab}}&{\mbox{otherwise}}\end{cases}}

является строгой архимедовой t-нормой и важным представителем параметрических классов t-норм Хамахера и t-норм Швейцера – Склара .

Свойства t-норм

Резкая t-норма — это наименьшая поточечно t-норма, а минимум — это наибольшая поточечно t-норма:

\top _{\mathrm {D} }(a,b)\leq \top (a,b)\leq \mathrm {\top _{min}} (a,b),

для любой t-нормы

\top

и все a , b в [0, 1].

Для каждой t-нормы T число 0 действует как нулевой элемент: T( a , 0) = 0 для всех a в [0, 1].

t-норма T имеет делители нуля тогда и только тогда, когда она имеет нильпотентные элементы; каждый нильпотентный элемент T также является делителем нуля T. Множество всех нильпотентных элементов представляет собой интервал [0, a ] или [0, a ), для некоторого a из [0, 1].

Свойства непрерывных t-норм

Хотя вещественные функции двух переменных могут быть непрерывными по каждой переменной, но не непрерывными на [0, 1] ², это не относится к t-нормам: t-норма T непрерывна тогда и только тогда, когда она непрерывна по одной переменной, т. е. тогда и только тогда, когда функции f _y ( x ) = T( x , y ) являются непрерывен для каждого y в [0, 1]. Аналогичные теоремы верны для непрерывности слева и справа t-нормы.

Непрерывная t-норма является архимедовой тогда и только тогда, когда 0 и 1 являются ее единственными идемпотентами .

Непрерывная архимедова t-норма является строгой, если 0 — ее единственный нильпотентный элемент; в противном случае оно нильпотентно. Более того, по определению непрерывная архимедова t-норма T нильпотентна тогда и только тогда, когда каждый x <1 является нильпотентным элементом T. Таким образом, при непрерывной архимедовой t-норме T либо все, либо ни один из элементов (0, 1) нильпотентны. Если все элементы в (0, 1) нильпотентны, то t-норма изоморфна t-норме Лукасевича; т. е. существует строго возрастающая функция f такая, что

\top (x,y)=f^{-1}(\top _{\mathrm {Luk} }(f(x),f(y))).

С другой стороны, если в T нет нильпотентных элементов, t-норма изоморфна произведению t-нормы. Другими словами, все нильпотентные t-нормы изоморфны, причем t-норма Лукасевича является их прототипным представителем; и все строгие t-нормы изоморфны, их прототипным примером является t-норма произведения. t-норма Лукасевича сама по себе изоморфна t-норме произведения, подрезанной на 0,25, т. е. функции p ( x , y ) = max(0,25, x ⋅ y ) на [0,25, 1] ².

Для каждой непрерывной t-нормы множество ее идемпотентов является замкнутым подмножеством [0, 1]. Таким образом, его дополнение — совокупность всех неидемпотентных элементов — представляет собой объединение счетного числа непересекающихся открытых интервалов. Ограничение t-нормы на любой из этих интервалов (включая его конечные точки) является архимедовым и, следовательно, изоморфно либо t-норме Лукасевича, либо t-норме произведения. Для таких x , y , которые не попадают в один и тот же открытый интервал неидемпотентов, t-норма равна минимуму x и y . Эти условия фактически дают характеристику непрерывных t-норм, называемую теоремой Мостерта-Шилдса , поскольку таким образом можно разложить каждую непрерывную t-норму, а описанная конструкция всегда дает непрерывную t-норму. Теорему можно также сформулировать следующим образом:

T-норма непрерывна тогда и только тогда, когда она изоморфна порядковой сумме минимума Лукасевича и произведения t-нормы.

Подобная характеризационная теорема для несплошных t-норм неизвестна (даже для непрерывных слева), лишь некоторые неисчерпывающие методы построения t-норм найдены .

Остальные

Для любой непрерывной слева t-нормы $\top$ , существует уникальная бинарная операция $\Rightarrow$ на [0, 1] такой, что

\top (z,x)\leq y

тогда и только тогда, когда

z\leq (x\Rightarrow y)

для всех x , y , z в [0, 1]. Эта операция называется невязкой t-нормы. В префиксной записи остаток t-нормы $\top$ часто обозначается ${\vec {\top }}$ или буквой Р.

Интервал [0, 1], снабженный t-нормой и ее остатком, образует решетку остатков . Отношение между t-нормой T и ее остатком R является примером присоединения (в частности, связи Галуа ): остаток образует правое сопряжение R( x , –) к функтору T(–, x ) для каждого x в решетка [0, 1] взята как категория ЧУМ .

В стандартной семантике нечеткой логики, основанной на t-норме, где конъюнкция интерпретируется t-нормой, остаток играет роль импликации (часто называемой R-импликацией ).

Основные свойства остатка

Если $\Rightarrow$ является остатком непрерывной слева t-нормы $\top$ , затем

(x\Rightarrow y)=\sup\{z\mid \top (z,x)\leq y\}.

Следовательно, для всех x , y в единичном интервале

(x\Rightarrow y)=1

тогда и только тогда, когда

x\leq y

и

(1\Rightarrow y)=y.

Если $*$ представляет собой непрерывную слева t-норму и $\Rightarrow$ его остаток, то

{\begin{array}{rcl}\min(x,y)&\geq &x*(x\Rightarrow y)\\\max(x,y)&=&\min((x\Rightarrow y)\Rightarrow y,(y\Rightarrow x)\Rightarrow x).\end{array}}

Если $*$ непрерывно, то в первом случае имеет место равенство.

Остаток общих непрерывных слева t-норм

Если x ≤ y , то R( x , y ) = 1 для любого остатка R. Поэтому в следующей таблице приведены значения заметных остатков только для x > y .

Оставшаяся часть	Имя	Значение для x > y	График
Минимальная Т-норма	Стандартное импликация Гёделя	и	Стандартная импликация Гёделя. Функция разрывна на прямой y = x < 1.
Т-норма продукта	Гогена Участие	y / x	Гогеновский смысл. Функция разрывна в точке x = y = 0.
Лукасевич t-норма	Стандартная импликация Лукасевича	1 – х + у	Стандартная импликация Лукасевича.
Нильпотентный минимум	Значение Фодора	макс(1 – х , у )	Остаток нильпотентного минимума. Функция разрывна на прямой 0 < y = x < 1.

Т-конормы

Т-конормы (также называемые S-нормами ) двойственны t-нормам при операции изменения порядка, которая присваивает 1 – x значению x на [0, 1]. Учитывая t-норму $\top$ , дополнительная конорма определяется формулой

\bot (a,b)=1-\top (1-a,1-b).

Это обобщает законы Де Моргана .

Отсюда следует, что t-конорма удовлетворяет следующим условиям, которые можно использовать для эквивалентного аксиоматического определения t-конормы независимо от t-норм:

Коммутативность: ⊥( a , b ) = ⊥( b , a )
Монотонность: ⊥( a , b ) ≤ ⊥( c , d ), если a ≤ c и b ≤ d
Ассоциативность: ⊥( a , ⊥( b , c )) = ⊥(⊥( a , b ), c )
Идентификатор: ⊥( a , 0) = a

Т-конормы используются для представления логической дизъюнкции в нечеткой логике и объединения в теории нечетких множеств .

Примеры т-конорм

Важными t-конормами являются те, которые двойственны выдающимся t-нормам:

График максимальной t-конормы (3D и контуры)

Максимальный t-конорм $\bot _{\mathrm {max} }(a,b)=\max\{a,b\}$ , двойственный минимальной t-норме, является наименьшей t-конормой (см. свойства t-конормы ниже). Это стандартная семантика для дизъюнкции в нечеткой логике Гёделя и для слабой дизъюнкции во всех нечетких логиках, основанных на t-норме.

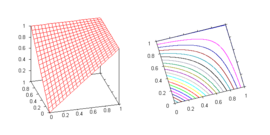
Вероятностная сумма $\bot _{\mathrm {sum} }(a,b)=a+b-a\cdot b=1-(1-a)\cdot (1-b)$ двойственна t-норме произведения. В теории вероятностей оно выражает вероятность объединения независимых событий . Это также стандартная семантика сильной дизъюнкции в таких расширениях нечеткой логики произведения , в которых она определима (например, в тех, которые содержат инволютивное отрицание).

Ограниченная сумма $\bot _{\mathrm {Luk} }(a,b)=\min\{a+b,1\}$ двойственна t-норме Лукасевича. Это стандартная семантика сильной дизъюнкции в нечеткой логике Лукасевича .

График радикальной t-конормы. Функция разрывна на прямых 1 > x = 0 и 1 > y = 0.

Резкий Т-конорм

\bot _{\mathrm {D} }(a,b)={\begin{cases}b&{\mbox{if }}a=0\\a&{\mbox{if }}b=0\\1&{\mbox{otherwise,}}\end{cases}}

двойственный радикальной t-норме, является наибольшей t-конормой (см. свойства t-конормы ниже).

График нильпотентного максимума. Функция разрывна на прямой 0 < x = 1 – y < 1.

Нильпотентный максимум , двойственный нильпотентному минимуму:

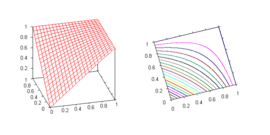
\bot _{\mathrm {nM} }(a,b)={\begin{cases}\max(a,b)&{\mbox{if }}a+b<1\\1&{\mbox{otherwise.}}\end{cases}}

Сумма Эйнштейна (сравните формулу сложения скоростей в специальной теории относительности)

\bot _{\mathrm {H} _{2}}(a,b)={\frac {a+b}{1+ab}}

является двойственным одной из t-норм Хамахера .

Свойства т-конормов

Многие свойства t-конорм можно получить путем дуализации свойств t-норм, например:

Для любой t-конормы ⊥ число 1 является аннулирующим элементом: ⊥( a , 1) = 1 для любого a из [0, 1].
В отличие от t-норм, все t-конормы ограничены максимальным и радикальным t-конормом:

\mathrm {\bot _{max}} (a,b)\leq \bot (a,b)\leq \bot _{\mathrm {D} }(a,b)

, для любого t-конорма

\bot

и все a , b в [0, 1].

Дополнительные свойства являются результатом отношений между t-нормами и t-конормами или их взаимодействием с другими операторами, например:

t-норма T распределяется по t-конорме ⊥, т. е.

T( x , ⊥( y , z )) = ⊥(T( x , y ), T( x , z )) для всех x , y , z в [0, 1],

тогда и только тогда, когда ⊥ — максимальная t-конорма. Двойственным образом любая t-конорма распределяется по минимуму, но не по любой другой t-норме.

Нестандартные отрицатели

отрицатель $n\colon [0,1]\to [0,1]$ — монотонно убывающее отображение такое, что $n(0)=1$ и $n(1)=0$ . Отрицатель n называется

строгий в случае строгой монотонности, и
сильным, если оно строго и инволютивно , т. е. $n(n(x))=x$ для всех $x$ в [0, 1].

Стандартный (канонический) отрицатель $n(x)=1-x,\ x\in [0,1]$ , одновременно строгий и сильный. Поскольку в приведенном выше определении пары t-норма/t-конорм используется стандартный отрицатель, его можно обобщить следующим образом:

Тройка Де Моргана — это тройка (T,⊥, n ) такая, что ^[1]

Т — это Т-норма
⊥ является t-конормой согласно аксиоматическому определению t-конормы, упомянутому выше.
n — сильный отрицатель
$\forall a,b\in [0,1]\colon \ n({\perp }(a,b))=\top (n(a),n(b))$ .

См. также

Ссылки

^ Исмат Бег, Самина Ашраф: Меры подобия для нечетких множеств , в: Applied and Computational Mathematics, март 2009 г., доступно на Research Gate с 23 ноября 2016 г.

Клемент, Эрих Петер; Месиар, Радко; и Пап, Эндре (2000), Треугольные нормы . Дордрехт: Клювер. ISBN 0-7923-6416-3 .
Гаек, Петр (1998), Метаматематика нечеткой логики . Дордрехт: Клювер. ISBN 0-7923-5238-6
Чиньоли, Роберто ЛО; Д'Оттавиано, Итала ML ; и Мундичи, Даниэле (2000), Алгебраические основы многозначного рассуждения . Дордрехт: Клювер. ISBN 0-7923-6009-5
Фодор, Янош (2004), «Непрерывные слева t-нормы в нечеткой логике: обзор». Акта Политехника Хунгарика 1 (2), ISSN 1785-8860 [1]

[1] Исмат Бег, Самина Ашраф: Меры подобия для нечетких множеств , в: Applied and Computational Mathematics, март 2009 г., доступно на Research Gate с 23 ноября 2016 г.

[1]