Нейронная сеть (машинное обучение)

| Part of a series on |
| Machine learning and data mining |
|---|
В машинном обучении нейронная сеть (также искусственная нейронная сеть или нейронная сеть , сокращенно ANN или NN ) — это модель, вдохновленная структурой и функцией биологических нейронных сетей животных в мозге . [1] [2]
ИНС состоит из связанных единиц или узлов, называемых искусственными нейронами , которые в общих чертах моделируют нейроны мозга. Они соединены ребрами , которые моделируют синапсы в мозге. Каждый искусственный нейрон получает сигналы от связанных нейронов, затем обрабатывает их и отправляет сигнал другим подключенным нейронам. «Сигнал» — это действительное число , а выход каждого нейрона вычисляется некоторой нелинейной функцией суммы его входов, называемой функцией активации . Сила сигнала при каждом соединении определяется весом , который корректируется в процессе обучения.
Обычно нейроны объединяются в слои. Разные слои могут выполнять разные преобразования на своих входах. Сигналы перемещаются от первого слоя ( входной слой ) к последнему уровню ( выходной уровень ), возможно, проходя через несколько промежуточных слоев ( скрытые слои ). Сеть обычно называется глубокой нейронной сетью, если она имеет как минимум два скрытых слоя. [3]
Искусственные нейронные сети используются для различных задач, включая прогнозное моделирование , адаптивное управление и решение задач в области искусственного интеллекта . Они могут учиться на собственном опыте и делать выводы из сложного и, казалось бы, несвязанного набора информации.
Обучение [ править ]
Neural networks are typically trained through empirical risk minimization. This method is based on the idea of optimizing the network's parameters to minimize the difference, or empirical risk, between the predicted output and the actual target values in a given dataset.[4] Gradient based methods such as backpropagation are usually used to estimate the parameters of the network.[4] During the training phase, ANNs learn from labeled training data by iteratively updating their parameters to minimize a defined loss function.[5] This method allows the network to generalize to unseen data.
In reality, textures and outlines would not be represented by single nodes, but rather by associated weight patterns of multiple nodes.
History[edit]
Historically, digital computers evolved from the von Neumann model, and operate via the execution of explicit instructions via access to memory by a number of processors. Neural networks, on the other hand, originated from efforts to model information processing in biological systems through the framework of connectionism. Unlike the von Neumann model, connectionist computing does not separate memory and processing.
The simplest kind of feedforward neural network (FNN) is a linear network, which consists of a single layer of output nodes; the inputs are fed directly to the outputs via a series of weights. The sum of the products of the weights and the inputs is calculated at each node. The mean squared errors between these calculated outputs and the given target values are minimized by creating an adjustment to the weights. This technique has been known for over two centuries as the method of least squares or linear regression. It was used as a means of finding a good rough linear fit to a set of points by Legendre (1805) and Gauss (1795) for the prediction of planetary movement.[7][8][9][10][11]
Warren McCulloch and Walter Pitts[12] (1943) also considered a non-learning computational model for neural networks.[13]
In the late 1940s, D. O. Hebb[14] created a learning hypothesis based on the mechanism of neural plasticity that became known as Hebbian learning. Hebbian learning is considered to be a 'typical' unsupervised learning rule and its later variants were early models for long term potentiation. These ideas started being applied to computational models in 1948 with Turing's "unorganized machines". Farley and Wesley A. Clark[15] were the first to simulate a Hebbian network in 1954 at MIT. They used computational machines, then called "calculators". Other neural network computational machines were created by Rochester, Holland, Habit, and Duda[16] in 1956. In 1958, psychologist Frank Rosenblatt invented the perceptron, the first implemented artificial neural network,[17][18][19][20] funded by the United States Office of Naval Research.[21]
The invention of the perceptron raised public excitement for research in Artificial Neural Networks, causing the US government to drastically increase funding into deep learning research. This led to "the golden age of AI" fueled by the optimistic claims made by computer scientists regarding the ability of perceptrons to emulate human intelligence.[22] For example, in 1957 Herbert Simon famously said:[22]
It is not my aim to surprise or shock you—but the simplest way I can summarize is to say that there are now in the world machines that think, that learn and that create. Moreover, their ability to do these things is going to increase rapidly until—in a visible future—the range of problems they can handle will be coextensive with the range to which the human mind has been applied.
However, this wasn't the case as research stagnated in the United States following the work of Minsky and Papert (1969),[23] who discovered that basic perceptrons were incapable of processing the exclusive-or circuit and that computers lacked sufficient power to train useful neural networks. This, along with other factors such as the 1973 Lighthill report by James Lighthill stating that research in Artificial Intelligence has not "produced the major impact that was then promised," shutting funding in research into the field of AI in all but two universities in the UK and in many major institutions across the world.[24] This ushered an era called the AI Winter with reduced research into connectionism due to a decrease in government funding and an increased stress on symbolic artificial intelligence in the United States and other Western countries.[25][24]
During the AI Winter era, however, research outside the United States continued, especially in Eastern Europe. By the time Minsky and Papert's book on Perceptrons came out, methods for training multilayer perceptrons (MLPs) were already known. The first deep learning MLP was published by Alexey Grigorevich Ivakhnenko and Valentin Lapa in 1965, as the Group Method of Data Handling.[26][27][28] The first deep learning MLP trained by stochastic gradient descent[29] was published in 1967 by Shun'ichi Amari.[30][31] In computer experiments conducted by Amari's student Saito, a five layer MLP with two modifiable layers learned useful internal representations to classify non-linearily separable pattern classes.[31]
Self-organizing maps (SOMs) were described by Teuvo Kohonen in 1982.[32][33] SOMs are neurophysiologically inspired[34] neural networks that learn low-dimensional representations of high-dimensional data while preserving the topological structure of the data. They are trained using competitive learning.[32]
The convolutional neural network (CNN) architecture with convolutional layers and downsampling layers was introduced by Kunihiko Fukushima in 1980.[35] He called it the neocognitron. In 1969, he also introduced the ReLU (rectified linear unit) activation function.[36][10] The rectifier has become the most popular activation function for CNNs and deep neural networks in general.[37] CNNs have become an essential tool for computer vision.
A key in later advances in artificial neural network research was the backpropagation algorithm, an efficient application of the Leibniz chain rule (1673)[38] to networks of differentiable nodes.[10] It is also known as the reverse mode of automatic differentiation or reverse accumulation, due to Seppo Linnainmaa (1970).[39][40][41][42][10] The term "back-propagating errors" was introduced in 1962 by Frank Rosenblatt,[43][10] but he did not have an implementation of this procedure, although Henry J. Kelley[44] and Bryson[45] had dynamic programming based continuous precursors of backpropagation[26][46][47][48] already in 1960–61 in the context of control theory.[10] In 1973, Dreyfus used backpropagation to adapt parameters of controllers in proportion to error gradients.[49] In 1982, Paul Werbos applied backpropagation to MLPs in the way that has become standard.[50][46] In 1986 Rumelhart, Hinton and Williams showed that backpropagation learned interesting internal representations of words as feature vectors when trained to predict the next word in a sequence.[51]
In the late 1970s to early 1980s, interest briefly emerged in theoretically investigating the Ising model created by Wilhelm Lenz (1920) and Ernst Ising (1925)[52] in relation to Cayley tree topologies and large neural networks. The Ising model is essentially a non-learning artificial recurrent neural network (RNN) consisting of neuron-like threshold elements.[10] In 1972, Shun'ichi Amari described an adaptive version of this architecture,[53][10] In 1981, the Ising model was solved exactly by Peter Barth for the general case of closed Cayley trees (with loops) with an arbitrary branching ratio[54] and found to exhibit unusual phase transition behavior in its local-apex and long-range site-site correlations.[55][56] John Hopfield popularised this architecture in 1982,[57] and it is now known as a Hopfield network.
The time delay neural network (TDNN) of Alex Waibel (1987) combined convolutions and weight sharing and backpropagation.[58][59] In 1988, Wei Zhang et al. applied backpropagation to a CNN (a simplified Neocognitron with convolutional interconnections between the image feature layers and the last fully connected layer) for alphabet recognition.[60][61] In 1989, Yann LeCun et al. trained a CNN to recognize handwritten ZIP codes on mail.[62] In 1992, max-pooling for CNNs was introduced by Juan Weng et al. to help with least-shift invariance and tolerance to deformation to aid 3D object recognition.[63][64][65] LeNet-5 (1998), a 7-level CNN by Yann LeCun et al.,[66] that classifies digits, was applied by several banks to recognize hand-written numbers on checks digitized in 32x32 pixel images.
From 1988 onward,[67][68] the use of neural networks transformed the field of protein structure prediction, in particular when the first cascading networks were trained on profiles (matrices) produced by multiple sequence alignments.[69]
In 1991, Sepp Hochreiter's diploma thesis [70] identified and analyzed the vanishing gradient problem[70][71] and proposed recurrent residual connections to solve it. His thesis was called "one of the most important documents in the history of machine learning" by his supervisor Juergen Schmidhuber.[10]
In 1991, Juergen Schmidhuber published adversarial neural networks that contest with each other in the form of a zero-sum game, where one network's gain is the other network's loss.[72][73][74] The first network is a generative model that models a probability distribution over output patterns. The second network learns by gradient descent to predict the reactions of the environment to these patterns. This was called "artificial curiosity."
In 1992, Juergen Schmidhuber proposed a hierarchy of RNNs pre-trained one level at a time by self-supervised learning.[75] It uses predictive coding to learn internal representations at multiple self-organizing time scales. This can substantially facilitate downstream deep learning. The RNN hierarchy can be collapsed into a single RNN, by distilling a higher level chunker network into a lower level automatizer network.[75][10] In the same year he also published an alternative to RNNs[76] which is a precursor of a linear Transformer.[77][78][10] It introduces the concept internal spotlights of attention:[79] a slow feedforward neural network learns by gradient descent to control the fast weights of another neural network through outer products of self-generated activation patterns.
The development of metal–oxide–semiconductor (MOS) very-large-scale integration (VLSI), in the form of complementary MOS (CMOS) technology, enabled increasing MOS transistor counts in digital electronics. This provided more processing power for the development of practical artificial neural networks in the 1980s.[80]
Neural networks' early successes included in 1995 a (mostly) self-driving car.[a][81]
1997, Sepp Hochreiter and Juergen Schmidhuber introduced the deep learning method called long short-term memory (LSTM), published in Neural Computation.[82] LSTM recurrent neural networks can learn "very deep learning" tasks[83] with long credit assignment paths that require memories of events that happened thousands of discrete time steps before. The "vanilla LSTM" with forget gate was introduced in 1999 by Felix Gers, Schmidhuber and Fred Cummins.[84]
Geoffrey Hinton et al. (2006) proposed learning a high-level representation using successive layers of binary or real-valued latent variables with a restricted Boltzmann machine[85] to model each layer. In 2012, Ng and Dean created a network that learned to recognize higher-level concepts, such as cats, only from watching unlabeled images.[86] Unsupervised pre-training and increased computing power from GPUs and distributed computing allowed the use of larger networks, particularly in image and visual recognition problems, which became known as "deep learning".[5]
Variants of the back-propagation algorithm, as well as unsupervised methods by Geoff Hinton and colleagues at the University of Toronto, can be used to train deep, highly nonlinear neural architectures,[87] similar to the 1980 Neocognitron by Kunihiko Fukushima,[88] and the "standard architecture of vision",[89] inspired by the simple and complex cells identified by David H. Hubel and Torsten Wiesel in the primary visual cortex.
Computational devices have been created in CMOS for both biophysical simulation and neuromorphic computing. More recent efforts show promise for creating nanodevices for very large scale principal components analyses and convolution.[90] If successful, these efforts could usher in a new era of neural computing that is a step beyond digital computing,[91] because it depends on learning rather than programming and because it is fundamentally analog rather than digital even though the first instantiations may in fact be with CMOS digital devices.
Ciresan and colleagues (2010)[92] showed that despite the vanishing gradient problem, GPUs make backpropagation feasible for many-layered feedforward neural networks.[93] Between 2009 and 2012, ANNs began winning prizes in image recognition contests, approaching human level performance on various tasks, initially in pattern recognition and handwriting recognition.[94][95] For example, the bi-directional and multi-dimensional long short-term memory (LSTM)[96][97] of Graves et al. won three competitions in connected handwriting recognition in 2009 without any prior knowledge about the three languages to be learned.[96][97]
Ciresan and colleagues built the first pattern recognizers to achieve human-competitive/superhuman performance[98] on benchmarks such as traffic sign recognition (IJCNN 2012).
Radial basis function and wavelet networks were introduced in 2013. These can be shown to offer best approximation properties and have been applied in nonlinear system identification and classification applications.[99]
In 2014, the adversarial network principle was used in a generative adversarial network (GAN) by Ian Goodfellow et al.[100] Here the adversarial network (discriminator) outputs a value between 1 and 0 depending on the likelihood of the first network's (generator) output is in a given set. This can be used to create realistic deepfakes.[101] Excellent image quality is achieved by Nvidia's StyleGAN (2018)[102] based on the Progressive GAN by Tero Karras, Timo Aila, Samuli Laine, and Jaakko Lehtinen.[103] Here the GAN generator is grown from small to large scale in a pyramidal fashion.
In 2015, Rupesh Kumar Srivastava, Klaus Greff, and Schmidhuber used the LSTM principle to create the Highway network, a feedforward neural network with hundreds of layers, much deeper than previous networks.[104][105] 7 months later, Kaiming He, Xiangyu Zhang; Shaoqing Ren, and Jian Sun won the ImageNet 2015 competition with an open-gated or gateless Highway network variant called Residual neural network.[106]
In 2017, Ashish Vaswani et al. introduced the modern Transformer architecture in their paper "Attention Is All You Need."[107] It combines this with a softmax operator and a projection matrix.[10] Transformers have increasingly become the model of choice for natural language processing.[108] Many modern large language models such as ChatGPT, GPT-4, and BERT use it. Transformers are also increasingly being used in computer vision.[109]
Ramenzanpour et al. showed in 2020 that analytical and computational techniques derived from statistical physics of disordered systems can be extended to large-scale problems, including machine learning, e.g., to analyze the weight space of deep neural networks.[110]
Models[edit]
This section may be confusing or unclear to readers. (April 2017) |

ANNs began as an attempt to exploit the architecture of the human brain to perform tasks that conventional algorithms had little success with. They soon reoriented towards improving empirical results, abandoning attempts to remain true to their biological precursors. ANNs have the ability to learn and model non-linearities and complex relationships. This is achieved by neurons being connected in various patterns, allowing the output of some neurons to become the input of others. The network forms a directed, weighted graph.[111]
An artificial neural network consists of simulated neurons. Each neuron is connected to other nodes via links like a biological axon-synapse-dendrite connection. All the nodes connected by links take in some data and use it to perform specific operations and tasks on the data. Each link has a weight, determining the strength of one node's influence on another,[112] allowing weights to choose the signal between neurons.
Artificial neurons[edit]
ANNs are composed of artificial neurons which are conceptually derived from biological neurons. Each artificial neuron has inputs and produces a single output which can be sent to multiple other neurons.[113] The inputs can be the feature values of a sample of external data, such as images or documents, or they can be the outputs of other neurons. The outputs of the final output neurons of the neural net accomplish the task, such as recognizing an object in an image.
To find the output of the neuron we take the weighted sum of all the inputs, weighted by the weights of the connections from the inputs to the neuron. We add a bias term to this sum.[114] This weighted sum is sometimes called the activation. This weighted sum is then passed through a (usually nonlinear) activation function to produce the output. The initial inputs are external data, such as images and documents. The ultimate outputs accomplish the task, such as recognizing an object in an image.[115]
Organization[edit]
The neurons are typically organized into multiple layers, especially in deep learning. Neurons of one layer connect only to neurons of the immediately preceding and immediately following layers. The layer that receives external data is the input layer. The layer that produces the ultimate result is the output layer. In between them are zero or more hidden layers. Single layer and unlayered networks are also used. Between two layers, multiple connection patterns are possible. They can be 'fully connected', with every neuron in one layer connecting to every neuron in the next layer. They can be pooling, where a group of neurons in one layer connects to a single neuron in the next layer, thereby reducing the number of neurons in that layer.[116] Neurons with only such connections form a directed acyclic graph and are known as feedforward networks.[117] Alternatively, networks that allow connections between neurons in the same or previous layers are known as recurrent networks.[118]
Hyperparameter[edit]
A hyperparameter is a constant parameter whose value is set before the learning process begins. The values of parameters are derived via learning. Examples of hyperparameters include learning rate, the number of hidden layers and batch size.[119] The values of some hyperparameters can be dependent on those of other hyperparameters. For example, the size of some layers can depend on the overall number of layers.
Learning[edit]
This section includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (August 2019) |
Learning is the adaptation of the network to better handle a task by considering sample observations. Learning involves adjusting the weights (and optional thresholds) of the network to improve the accuracy of the result. This is done by minimizing the observed errors. Learning is complete when examining additional observations does not usefully reduce the error rate. Even after learning, the error rate typically does not reach 0. If after learning, the error rate is too high, the network typically must be redesigned. Practically this is done by defining a cost function that is evaluated periodically during learning. As long as its output continues to decline, learning continues. The cost is frequently defined as a statistic whose value can only be approximated. The outputs are actually numbers, so when the error is low, the difference between the output (almost certainly a cat) and the correct answer (cat) is small. Learning attempts to reduce the total of the differences across the observations. Most learning models can be viewed as a straightforward application of optimization theory and statistical estimation.[111][120]
Learning rate[edit]
The learning rate defines the size of the corrective steps that the model takes to adjust for errors in each observation.[121] A high learning rate shortens the training time, but with lower ultimate accuracy, while a lower learning rate takes longer, but with the potential for greater accuracy. Optimizations such as Quickprop are primarily aimed at speeding up error minimization, while other improvements mainly try to increase reliability. In order to avoid oscillation inside the network such as alternating connection weights, and to improve the rate of convergence, refinements use an adaptive learning rate that increases or decreases as appropriate.[122] The concept of momentum allows the balance between the gradient and the previous change to be weighted such that the weight adjustment depends to some degree on the previous change. A momentum close to 0 emphasizes the gradient, while a value close to 1 emphasizes the last change.
Cost function[edit]
While it is possible to define a cost function ad hoc, frequently the choice is determined by the function's desirable properties (such as convexity) or because it arises from the model (e.g. in a probabilistic model the model's posterior probability can be used as an inverse cost).
Backpropagation[edit]
Backpropagation is a method used to adjust the connection weights to compensate for each error found during learning. The error amount is effectively divided among the connections. Technically, backprop calculates the gradient (the derivative) of the cost function associated with a given state with respect to the weights. The weight updates can be done via stochastic gradient descent or other methods, such as extreme learning machines,[123] "no-prop" networks,[124] training without backtracking,[125] "weightless" networks,[126][127] and non-connectionist neural networks.[citation needed]
Learning paradigms[edit]
This section includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (August 2019) |
Machine learning is commonly separated into three main learning paradigms, supervised learning,[128] unsupervised learning[129] and reinforcement learning.[130] Each corresponds to a particular learning task.
Supervised learning[edit]
Supervised learning uses a set of paired inputs and desired outputs. The learning task is to produce the desired output for each input. In this case, the cost function is related to eliminating incorrect deductions.[131] A commonly used cost is the mean-squared error, which tries to minimize the average squared error between the network's output and the desired output. Tasks suited for supervised learning are pattern recognition (also known as classification) and regression (also known as function approximation). Supervised learning is also applicable to sequential data (e.g., for handwriting, speech and gesture recognition). This can be thought of as learning with a "teacher", in the form of a function that provides continuous feedback on the quality of solutions obtained thus far.
Unsupervised learning[edit]
In unsupervised learning, input data is given along with the cost function, some function of the data and the network's output. The cost function is dependent on the task (the model domain) and any a priori assumptions (the implicit properties of the model, its parameters and the observed variables). As a trivial example, consider the model where is a constant and the cost . Minimizing this cost produces a value of that is equal to the mean of the data. The cost function can be much more complicated. Its form depends on the application: for example, in compression it could be related to the mutual information between and , whereas in statistical modeling, it could be related to the posterior probability of the model given the data (note that in both of those examples, those quantities would be maximized rather than minimized). Tasks that fall within the paradigm of unsupervised learning are in general estimation problems; the applications include clustering, the estimation of statistical distributions, compression and filtering.
Reinforcement learning[edit]
In applications such as playing video games, an actor takes a string of actions, receiving a generally unpredictable response from the environment after each one. The goal is to win the game, i.e., generate the most positive (lowest cost) responses. In reinforcement learning, the aim is to weight the network (devise a policy) to perform actions that minimize long-term (expected cumulative) cost. At each point in time the agent performs an action and the environment generates an observation and an instantaneous cost, according to some (usually unknown) rules. The rules and the long-term cost usually only can be estimated. At any juncture, the agent decides whether to explore new actions to uncover their costs or to exploit prior learning to proceed more quickly.
Formally the environment is modeled as a Markov decision process (MDP) with states and actions . Because the state transitions are not known, probability distributions are used instead: the instantaneous cost distribution , the observation distribution and the transition distribution , while a policy is defined as the conditional distribution over actions given the observations. Taken together, the two define a Markov chain (MC). The aim is to discover the lowest-cost MC.
ANNs serve as the learning component in such applications.[132][133] Dynamic programming coupled with ANNs (giving neurodynamic programming)[134] has been applied to problems such as those involved in vehicle routing,[135] video games, natural resource management[136][137] and medicine[138] because of ANNs ability to mitigate losses of accuracy even when reducing the discretization grid density for numerically approximating the solution of control problems. Tasks that fall within the paradigm of reinforcement learning are control problems, games and other sequential decision making tasks.
Self-learning[edit]
Self-learning in neural networks was introduced in 1982 along with a neural network capable of self-learning named crossbar adaptive array (CAA).[139] It is a system with only one input, situation s, and only one output, action (or behavior) a. It has neither external advice input nor external reinforcement input from the environment. The CAA computes, in a crossbar fashion, both decisions about actions and emotions (feelings) about encountered situations. The system is driven by the interaction between cognition and emotion.[140] Given the memory matrix, W =||w(a,s)||, the crossbar self-learning algorithm in each iteration performs the following computation:
In situation s perform action a; Receive consequence situation s'; Compute emotion of being in consequence situation v(s'); Update crossbar memory w'(a,s) = w(a,s) + v(s').
The backpropagated value (secondary reinforcement) is the emotion toward the consequence situation. The CAA exists in two environments, one is behavioral environment where it behaves, and the other is genetic environment, where from it initially and only once receives initial emotions about to be encountered situations in the behavioral environment. Having received the genome vector (species vector) from the genetic environment, the CAA will learn a goal-seeking behavior, in the behavioral environment that contains both desirable and undesirable situations.[141]
Neuroevolution[edit]
Neuroevolution can create neural network topologies and weights using evolutionary computation. It is competitive with sophisticated gradient descent approaches[citation needed]. One advantage of neuroevolution is that it may be less prone to get caught in "dead ends".[142]
Stochastic neural network[edit]
Stochastic neural networks originating from Sherrington–Kirkpatrick models are a type of artificial neural network built by introducing random variations into the network, either by giving the network's artificial neurons stochastic transfer functions, or by giving them stochastic weights. This makes them useful tools for optimization problems, since the random fluctuations help the network escape from local minima.[143] Stochastic neural networks trained using a Bayesian approach are known as Bayesian neural networks.[144]
Other[edit]
In a Bayesian framework, a distribution over the set of allowed models is chosen to minimize the cost. Evolutionary methods,[145] gene expression programming,[146] simulated annealing,[147] expectation–maximization, non-parametric methods and particle swarm optimization[148] are other learning algorithms. Convergent recursion is a learning algorithm for cerebellar model articulation controller (CMAC) neural networks.[149][150]
Modes[edit]
This section includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (August 2019) |
Two modes of learning are available: stochastic and batch. In stochastic learning, each input creates a weight adjustment. In batch learning weights are adjusted based on a batch of inputs, accumulating errors over the batch. Stochastic learning introduces "noise" into the process, using the local gradient calculated from one data point; this reduces the chance of the network getting stuck in local minima. However, batch learning typically yields a faster, more stable descent to a local minimum, since each update is performed in the direction of the batch's average error. A common compromise is to use "mini-batches", small batches with samples in each batch selected stochastically from the entire data set.
Types[edit]
ANNs have evolved into a broad family of techniques that have advanced the state of the art across multiple domains. The simplest types have one or more static components, including number of units, number of layers, unit weights and topology. Dynamic types allow one or more of these to evolve via learning. The latter is much more complicated but can shorten learning periods and produce better results. Some types allow/require learning to be "supervised" by the operator, while others operate independently. Some types operate purely in hardware, while others are purely software and run on general purpose computers.
Some of the main breakthroughs include:
- Convolutional neural networks that have proven particularly successful in processing visual and other two-dimensional data;[151][152] where long short-term memory avoids the vanishing gradient problem[153] and can handle signals that have a mix of low and high frequency components aiding large-vocabulary speech recognition,[154][155] text-to-speech synthesis,[156][46][157] and photo-real talking heads;[158]
- Competitive networks such as generative adversarial networks in which multiple networks (of varying structure) compete with each other, on tasks such as winning a game[159] or on deceiving the opponent about the authenticity of an input.[100]
Network design[edit]
Using artificial neural networks requires an understanding of their characteristics.
- Choice of model: This depends on the data representation and the application. Model parameters include the number, type, and connectedness of network layers, as well as the size of each and the connection type (full, pooling, etc. ). Overly complex models learn slowly.
- Learning algorithm: Numerous trade-offs exist between learning algorithms. Almost any algorithm will work well with the correct hyperparameters[160] for training on a particular data set. However, selecting and tuning an algorithm for training on unseen data requires significant experimentation.
- Robustness: If the model, cost function and learning algorithm are selected appropriately, the resulting ANN can become robust.
Neural architecture search (NAS) uses machine learning to automate ANN design. Various approaches to NAS have designed networks that compare well with hand-designed systems. The basic search algorithm is to propose a candidate model, evaluate it against a dataset, and use the results as feedback to teach the NAS network.[161] Available systems include AutoML and AutoKeras.[162] scikit-learn library provides functions to help with building a deep network from scratch. We can then implement a deep network with TensorFlow or Keras.
Hyperparameters must also be defined as part of the design (they are not learned), governing matters such as how many neurons are in each layer, learning rate, step, stride, depth, receptive field and padding (for CNNs), etc.[163]
The Python code snippet provides an overview of the training function, which uses the training dataset, number of hidden layer units, learning rate, and number of iterations as parameters:def train(X, y, n_hidden, learning_rate, n_iter):
m, n_input = X.shape
# 1. random initialize weights and biases
w1 = np.random.randn(n_input, n_hidden)
b1 = np.zeros((1, n_hidden))
w2 = np.random.randn(n_hidden, 1)
b2 = np.zeros((1, 1))
# 2. in each iteration, feed all layers with the latest weights and biases
for i in range(n_iter + 1):
z2 = np.dot(X, w1) + b1
a2 = sigmoid(z2)
z3 = np.dot(a2, w2) + b2
a3 = z3
dz3 = a3 - y
dw2 = np.dot(a2.T, dz3)
db2 = np.sum(dz3, axis=0, keepdims=True)
dz2 = np.dot(dz3, w2.T) * sigmoid_derivative(z2)
dw1 = np.dot(X.T, dz2)
db1 = np.sum(dz2, axis=0)
# 3. update weights and biases with gradients
w1 -= learning_rate * dw1 / m
w2 -= learning_rate * dw2 / m
b1 -= learning_rate * db1 / m
b2 -= learning_rate * db2 / m
if i % 1000 == 0:
print("Epoch", i, "loss: ", np.mean(np.square(dz3)))
model = {"w1": w1, "b1": b1, "w2": w2, "b2": b2}
return model
Applications[edit]
Because of their ability to reproduce and model nonlinear processes, artificial neural networks have found applications in many disciplines. These include:
- Function approximation,[164] or regression analysis,[165] (including time series prediction, fitness approximation,[166] and modeling)
- Data processing[167] (including filtering, clustering, blind source separation,[168] and compression)
- Nonlinear system identification[99] and control (including vehicle control, trajectory prediction,[169] adaptive control, process control, and natural resource management)
- Pattern recognition (including radar systems, face identification, signal classification,[170] novelty detection, 3D reconstruction,[171] object recognition, and sequential decision making[172])
- Sequence recognition (including gesture, speech, and handwritten and printed text recognition[173])
- Sensor data analysis[174] (including image analysis)
- Robotics (including directing manipulators and prostheses)
- Data mining (including knowledge discovery in databases)
- Finance[175] (such as ex-ante models for specific financial long-run forecasts and artificial financial markets)
- Quantum chemistry[176]
- General game playing[177]
- Generative AI[178]
- Data visualization
- Machine translation
- Social network filtering[179]
- E-mail spam filtering
- Medical diagnosis
ANNs have been used to diagnose several types of cancers[180][181] and to distinguish highly invasive cancer cell lines from less invasive lines using only cell shape information.[182][183]
ANNs have been used to accelerate reliability analysis of infrastructures subject to natural disasters[184][185] and to predict foundation settlements.[186] It can also be useful to mitigate flood by the use of ANNs for modelling rainfall-runoff.[187] ANNs have also been used for building black-box models in geoscience: hydrology,[188][189] ocean modelling and coastal engineering,[190][191] and geomorphology.[192] ANNs have been employed in cybersecurity, with the objective to discriminate between legitimate activities and malicious ones. For example, machine learning has been used for classifying Android malware,[193] for identifying domains belonging to threat actors and for detecting URLs posing a security risk.[194] Research is underway on ANN systems designed for penetration testing, for detecting botnets,[195] credit cards frauds[196] and network intrusions.
ANNs have been proposed as a tool to solve partial differential equations in physics[197][198][199] and simulate the properties of many-body open quantum systems.[200][201][202][203] In brain research ANNs have studied short-term behavior of individual neurons,[204] the dynamics of neural circuitry arise from interactions between individual neurons and how behavior can arise from abstract neural modules that represent complete subsystems. Studies considered long-and short-term plasticity of neural systems and their relation to learning and memory from the individual neuron to the system level.
It is possible to create a profile of a user's interests from pictures, using artificial neural networks trained for object recognition.[205]
Beyond their traditional applications, artificial neural networks are increasingly being utilized in interdisciplinary research, such as materials science. For instance, graph neural networks (GNNs) have demonstrated their capability in scaling deep learning for the discovery of new stable materials by efficiently predicting the total energy of crystals. This application underscores the adaptability and potential of ANNs in tackling complex problems beyond the realms of predictive modeling and artificial intelligence, opening new pathways for scientific discovery and innovation.[206]
Theoretical properties[edit]
Computational power[edit]
The multilayer perceptron is a universal function approximator, as proven by the universal approximation theorem. However, the proof is not constructive regarding the number of neurons required, the network topology, the weights and the learning parameters.
A specific recurrent architecture with rational-valued weights (as opposed to full precision real number-valued weights) has the power of a universal Turing machine,[207] using a finite number of neurons and standard linear connections. Further, the use of irrational values for weights results in a machine with super-Turing power.[208][209][failed verification]
Capacity[edit]
Свойство модели «емкость» соответствует ее способности моделировать любую заданную функцию. Это связано с объемом информации, которая может храниться в сети, и с понятием сложности. Сообществу известны два понятия емкости. Информационная емкость и размерность венчурного капитала. Информационная емкость перцептрона интенсивно обсуждается в книге сэра Дэвида Маккея. [210] который суммирует работу Томаса Ковера. [211] Емкость сети стандартных нейронов (не сверточных) можно определить по четырем правилам: [212] которые вытекают из понимания нейрона как электрического элемента. Информационная емкость охватывает функции, моделируемые сетью, если на входе имеются любые данные. Второе понятие — это размер венчурного капитала . VC Dimension использует принципы теории меры и находит максимальную мощность при наилучших возможных обстоятельствах. Это если ввести входные данные в определенном виде. Как отмечается в, [210] Размерность VC для произвольных входных данных составляет половину информационной емкости персептрона. Размер VC для произвольных точек иногда называют объемом памяти. [213]
Конвергенция [ править ]
Модели могут не всегда сходиться к единому решению, во-первых, потому, что могут существовать локальные минимумы, в зависимости от функции стоимости и модели. Во-вторых, используемый метод оптимизации может не гарантировать сходимость, когда он начинается далеко от любого локального минимума. В-третьих, при достаточно больших данных или параметрах некоторые методы становятся непрактичными.
Еще одна проблема, о которой стоит упомянуть, заключается в том, что обучение может пересечь некоторую седловую точку , что может привести к сближению в неправильном направлении.
Поведение конвергенции определенных типов архитектур ИНС более понятно, чем других. Когда ширина сети приближается к бесконечности, ИНС хорошо описывается расширением Тейлора первого порядка на протяжении всего обучения и, таким образом, наследует поведение сходимости аффинных моделей . [214] [215] Другой пример: когда параметры малы, замечено, что ИНС часто соответствуют целевым функциям от низких до высоких частот. Такое поведение называется спектральным смещением или частотным принципом нейронных сетей. [216] [217] [218] [219] Это явление противоположно поведению некоторых хорошо изученных итерационных численных схем, таких как метод Якоби . Было замечено, что более глубокие нейронные сети более склонны к низкочастотным функциям. [220]
Обобщение и статистика [ править ]
Этот раздел включает список использованной литературы , связанной литературы или внешних ссылок , но его источники остаются неясными, поскольку в нем отсутствуют встроенные цитаты . ( Август 2019 г. ) |
Приложения, целью которых является создание системы, которая хорошо обобщает невидимые примеры, сталкиваются с возможностью переобучения. Это возникает в запутанных или переопределенных системах, когда пропускная способность сети значительно превышает необходимые свободные параметры. Два подхода касаются перетренированности. Первый — использовать перекрестную проверку и подобные методы для проверки наличия переобучения и выбора гиперпараметров для минимизации ошибки обобщения.
Второй — использовать некоторую форму регуляризации . Эта концепция возникает в вероятностной (байесовской) структуре, где регуляризация может быть выполнена путем выбора большей априорной вероятности среди более простых моделей; но также и в статистической теории обучения, где целью является минимизация двух величин: «эмпирического риска» и «структурного риска», который примерно соответствует ошибке в обучающем наборе и прогнозируемой ошибке в невидимых данных из-за переобучения.

Контролируемые нейронные сети, использующие функцию стоимости среднеквадратической ошибки (MSE), могут использовать формальные статистические методы для определения достоверности обученной модели. MSE в наборе проверки можно использовать в качестве оценки дисперсии. Затем это значение можно использовать для расчета доверительного интервала выходных данных сети, предполагая нормальное распределение . Проведенный таким образом доверительный анализ является статистически достоверным до тех пор, пока распределение выходных вероятностей остается прежним и сеть не изменяется.
Присвоив функцию активации softmax , обобщение логистической функции , на выходном слое нейронной сети (или компоненту softmax в сети, основанной на компонентах) для категориальных целевых переменных, выходные данные можно интерпретировать как апостериорные вероятности. Это полезно при классификации, поскольку дает меру достоверности классификаций.
Функция активации softmax:
Критика [ править ]
Обучение [ править ]
Распространенная критика нейронных сетей, особенно в робототехнике, заключается в том, что им требуется слишком много обучающих выборок для реальной работы. [221] Любая обучающаяся машина нуждается в достаточном количестве репрезентативных примеров, чтобы уловить основную структуру, позволяющую обобщать ее на новые случаи. Потенциальные решения включают случайное перетасовывание обучающих примеров с использованием алгоритма числовой оптимизации, который не делает слишком больших шагов при изменении сетевых подключений по примеру, группировку примеров в так называемые мини-пакеты и/или введение рекурсивного алгоритма наименьших квадратов для CMAC. . [149] Дин Померло использует нейронную сеть для обучения роботизированного транспортного средства езде по нескольким типам дорог (однополосные, многополосные, грунтовые и т. д.), и большой объем его исследований посвящен экстраполяции нескольких сценариев обучения на основе одного обучения. опыт и сохранение разнообразия прошлых тренировок, чтобы система не перетренировалась (если, например, ей предлагается серия поворотов направо — она не должна учиться всегда поворачивать направо). [222]
Теория [ править ]
Центральная претензия [ нужна ссылка ] ИНС заключается в том, что они воплощают в себе новые и мощные общие принципы обработки информации. Эти принципы нечетко определены. Часто утверждают [ кем? ] что они возникают из самой сети. Это позволяет описать простую статистическую ассоциацию (основную функцию искусственных нейронных сетей) как обучение или распознавание. В 1997 году Александр Дьюдни , бывший обозреватель Scientific American , заметил, что в результате искусственные нейронные сети приобретают «качество «что-то ради ничего», которое придает особую ауру лени и явное отсутствие любопытства по поводу того, насколько хороши эти сети. вычислительные системы не вмешиваются; решения находятся как по волшебству, и никто, кажется, ничему не научился». [223] Один из ответов Дьюдни заключается в том, что нейронные сети успешно используются для решения многих сложных и разнообразных задач, начиная от автономного управления самолетом [224] от обнаружения мошенничества с кредитными картами до овладения игрой в го .
Писатель-технолог Роджер Бриджмен прокомментировал:
Нейронные сети, например, находятся на скамье подсудимых не только потому, что их разрекламировали до небес (а что нет?), но и потому, что вы можете создать успешную сеть, не понимая, как она работает: набор чисел, фиксирующих ее поведение, по всей вероятности, будет «непрозрачной, нечитаемой таблицей… бесполезной как научный ресурс».
Несмотря на свое решительное заявление о том, что наука — это не технология, Дьюдни, похоже, выставляет нейронные сети к позорному столбу как плохую науку, тогда как большинство из тех, кто их разрабатывает, просто пытаются быть хорошими инженерами. Нечитаемая таблица, которую может прочитать полезная машина, все равно стоит иметь. [225]
Хотя это правда, что анализировать то, что было изучено искусственной нейронной сетью, сложно, сделать это гораздо проще, чем анализировать то, что было изучено биологической нейронной сетью. Более того, недавний акцент на объяснимости ИИ способствовал развитию методов, особенно основанных на механизмах внимания , для визуализации и объяснения изученных нейронных сетей. Более того, исследователи, изучающие алгоритмы обучения нейронных сетей, постепенно раскрывают общие принципы, которые позволяют обучающимся машинам быть успешными. Например, Бенджио и ЛеКун (2007) написали статью о локальном и нелокальном обучении, а также о поверхностной и глубокой архитектуре. [226]
Биологический мозг использует как поверхностные, так и глубокие цепи, как сообщает анатомия мозга. [227] демонстрируя широкий спектр инвариантности. Венг [228] утверждал, что мозг самостоятельно подключается в основном в соответствии со статистикой сигналов, и поэтому последовательный каскад не может уловить все основные статистические зависимости.
Аппаратное обеспечение [ править ]
Большие и эффективные нейронные сети требуют значительных вычислительных ресурсов. [229] Хотя в мозгу есть аппаратное обеспечение, предназначенное для обработки сигналов через граф нейронов, моделирование даже упрощенного нейрона на архитектуре фон Неймана может потребовать огромных объемов памяти и хранилища. Более того, разработчику часто приходится передавать сигналы через многие из этих соединений и связанных с ними нейронов, что требует огромной мощности процессора и времени.
Шмидхубер отметил, что возрождение нейронных сетей в двадцать первом веке во многом связано с достижениями в области аппаратного обеспечения: с 1991 по 2015 год вычислительная мощность, особенно с помощью GPGPU (на графических процессорах ), увеличилась примерно в миллион раз, в результате чего стандартный алгоритм обратного распространения ошибки возможен для обучающих сетей, которые находятся на несколько уровней глубже, чем раньше. [26] Использование ускорителей, таких как FPGA и GPU, может сократить время обучения с месяцев до дней. [229]
Нейроморфная инженерия или физическая нейронная сеть напрямую решают аппаратные трудности, создавая чипы, не относящиеся к фон Нейману, для непосредственной реализации нейронных сетей в схемах. Другой тип чипа, оптимизированный для обработки нейронных сетей, называется тензорным процессором или TPU. [230]
контрпримеры Практические
Анализировать то, что было изучено ИНС, гораздо проще, чем анализировать то, что было изучено биологической нейронной сетью. Более того, исследователи, изучающие алгоритмы обучения нейронных сетей, постепенно раскрывают общие принципы, которые позволяют обучающимся машинам быть успешными. Например, локальное и нелокальное обучение и поверхностная и глубокая архитектура. [231]
Гибридные подходы [ править ]
Сторонники гибридных моделей (объединяющих нейронные сети и символические подходы) говорят, что такая смесь может лучше отразить механизмы человеческого разума. [232] [233]
Смещение набора данных [ править ]
Нейронные сети зависят от качества данных, на которых они обучаются, поэтому данные низкого качества с несбалансированной репрезентативностью могут привести к обучению модели и закреплению социальных предубеждений. [234] [235] Эти унаследованные предубеждения становятся особенно критичными, когда ИНС интегрируются в реальные сценарии, где обучающие данные могут быть несбалансированными из-за нехватки данных для конкретной расы, пола или другого признака. [234] Этот дисбаланс может привести к тому, что модель будет иметь неадекватное представление и понимание недостаточно представленных групп, что приведет к дискриминационным результатам, которые усугубят социальное неравенство, особенно в таких приложениях, как распознавание лиц , процессы найма и правоохранительная деятельность . [235] [236] Например, в 2018 году Amazon пришлось отказаться от инструмента подбора персонала, потому что модель отдавала предпочтение мужчинам, а не женщинам на должностях в области разработки программного обеспечения из-за большего количества работников-мужчин в этой области. [236] Программа будет наказывать любое резюме со словом «женщина» или названием любого женского колледжа. Однако использование синтетических данных может помочь уменьшить предвзятость набора данных и повысить представленность в наборах данных. [237]
Галерея [ править ]
-
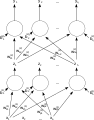
Однослойная искусственная нейронная сеть прямого распространения. Стрелки, исходящие из опущены для ясности. Эта сеть имеет p входов и q выходов. В этой системе значение q-го выхода, , рассчитывается как
-
Двухслойная искусственная нейронная сеть прямого распространения
-
Искусственная нейронная сеть
-
Граф зависимости ИНС
-
Однослойная искусственная нейронная сеть прямого распространения с 4 входами, 6 скрытыми узлами и 2 выходами. Учитывая состояние положения и направление, он выводит значения управления на основе колеса.
-
Двухслойная искусственная нейронная сеть прямого распространения с 8 входами, скрытыми узлами 2x8 и 2 выходами. Учитывая состояние положения, направление и другие значения окружающей среды, он выводит управляющие значения на основе подруливающего устройства.
-
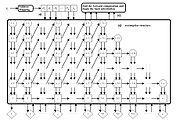
Параллельная конвейерная структура нейронной сети CMAC. Этот алгоритм обучения может сходиться за один шаг.
Последние достижения и будущие направления [ править ]
Искусственные нейронные сети (ИНС) претерпели значительные усовершенствования, особенно в их способности моделировать сложные системы, обрабатывать большие наборы данных и адаптироваться к различным типам приложений. Их эволюция за последние несколько десятилетий была отмечена широким спектром приложений в таких областях, как обработка изображений, распознавание речи, обработка естественного языка, финансы и медицина.
Обработка изображений [ править ]
В области обработки изображений ИНС используются в таких задачах, как классификация изображений, распознавание объектов и сегментация изображений. Например, глубокие сверточные нейронные сети (CNN) сыграли важную роль в распознавании рукописных цифр, обеспечив современную производительность. [238] Это демонстрирует способность ИНС эффективно обрабатывать и интерпретировать сложную визуальную информацию, что приводит к прогрессу в самых разных областях: от автоматического наблюдения до медицинской визуализации. [238]
Распознавание речи [ править ]
Моделируя речевые сигналы, ИНС используются для таких задач, как идентификация говорящего и преобразование речи в текст. Архитектура глубоких нейронных сетей внесла значительные улучшения в распознавание непрерывной речи с большим словарным запасом, превосходя традиционные методы. [238] [239] Эти достижения позволили разработать более точные и эффективные системы с голосовым управлением, улучшающие пользовательские интерфейсы в технологических продуктах.
Обработка естественного языка [ править ]
При обработке естественного языка ИНС используются для таких задач, как классификация текста, анализ настроений и машинный перевод. Они позволили разработать модели, которые могут точно переводить между языками, понимать контекст и тональность текстовых данных, а также классифицировать текст на основе содержания. [238] [239] Это имеет значение для автоматизированного обслуживания клиентов, модерации контента и технологий понимания языка.
Системы управления [ править ]
В области систем управления ИНС используются для моделирования динамических систем для таких задач, как идентификация системы, проектирование управления и оптимизация. Например, нейронные сети глубокого прямого распространения важны в приложениях идентификации и управления системами.
Финансы [ править ]
ИНС используются для прогнозирования фондового рынка и кредитного скоринга :
- При инвестировании ИНС могут обрабатывать огромные объемы финансовых данных, распознавать сложные закономерности и прогнозировать тенденции фондового рынка, помогая инвесторам и риск-менеджерам принимать обоснованные решения. [238]
- В кредитном скоринге ИНС предлагают персонализированную оценку кредитоспособности на основе данных, повышая точность прогнозов дефолта и автоматизируя процесс кредитования. [239]
ИНС требуют высококачественных данных и тщательной настройки, а их природа «черного ящика» может создавать проблемы при интерпретации. Тем не менее, продолжающиеся достижения позволяют предположить, что ИНС продолжают играть роль в финансах, предлагая ценную информацию и улучшая стратегии управления рисками .
Медицина [ править ]
ИНС способны обрабатывать и анализировать огромные наборы медицинских данных. Они повышают точность диагностики, особенно за счет интерпретации сложных медицинских изображений для раннего выявления заболеваний и прогнозирования результатов лечения пациентов для индивидуального планирования лечения. [239] При открытии лекарств ИНС ускоряют идентификацию потенциальных кандидатов на лекарства и прогнозируют их эффективность и безопасность, значительно сокращая время и затраты на разработку. [238] Кроме того, их применение в персонализированной медицине и анализе данных здравоохранения позволяет разрабатывать индивидуальные методы лечения и эффективно управлять уходом за пациентами. [239] Продолжающиеся исследования направлены на решение остающихся проблем, таких как конфиденциальность данных и интерпретируемость моделей, а также расширение сферы применения ИНС в медицине.
Создание контента [ править ]
ИНС, такие как генеративно-состязательные сети ( GAN ) и преобразователи, используются для создания контента во многих отраслях. [240] Это связано с тем, что модели глубокого обучения способны изучать стиль художника или музыканта на основе огромных наборов данных и создавать совершенно новые произведения искусства и музыкальные композиции. Например, DALL-E — это глубокая нейронная сеть, обученная на 650 миллионах пар изображений и текстов в Интернете, которая может создавать произведения искусства на основе текста, введенного пользователем. [241] В области музыки трансформеры используются для создания оригинальной музыки для рекламных роликов и документальных фильмов такими компаниями, как AIVA и Jukedeck . [242] В маркетинговой индустрии генеративные модели используются для создания персонализированной рекламы для потребителей. [240] Кроме того, крупные кинокомпании сотрудничают с технологическими компаниями для анализа финансового успеха фильма, например, партнерство между Warner Bros и технологической компанией Cinelytic, основанное в 2020 году. [243] Кроме того, нейронные сети нашли применение при создании видеоигр, где неигровые персонажи (NPC) могут принимать решения на основе всех персонажей, находящихся в данный момент в игре. [244]
См. также [ править ]
- АДАЛИН
- Автоэнкодер
- Биологические вычисления
- Проект Голубого Мозга
- Катастрофическое вмешательство
- Когнитивная архитектура
- Коннекционистская экспертная система
- Коннектомика
- Глубокое изображение до
- Цифровой морфогенез
- Эффективно обновляемая нейронная сеть
- Эволюционный алгоритм
- Генетический алгоритм
- Гиперпространственные вычисления
- Адаптивное табулирование на месте
- Большие ограничения ширины нейронных сетей
- Список концепций машинного обучения
- Мемристор
- Нейронный газ
- Программное обеспечение для нейронных сетей
- Оптическая нейронная сеть
- Параллельная распределенная обработка
- Философия искусственного интеллекта
- Прогнозная аналитика
- Квантовая нейронная сеть
- Машина опорных векторов
- Пиковая нейронная сеть
- Стохастический попугай
- Тензорная продуктовая сеть
Внешние ссылки [ править ]
- Краткое введение в нейронные сети (Д. Кризель) — иллюстрированная двуязычная рукопись об искусственных нейронных сетях; Темы на данный момент: перцептроны, обратное распространение ошибки, радиальные базисные функции, рекуррентные нейронные сети, самоорганизующиеся карты, сети Хопфилда.
- Обзор нейронных сетей в материаловедении. Архивировано 7 июня 2015 г. в Wayback Machine.
- Учебное пособие по искусственным нейронным сетям на трех языках (Мадридский политехнический университет)
- Еще одно знакомство с ИНС
- Следующее поколение нейронных сетей. Архивировано 24 января 2011 г. в Wayback Machine — Google Tech Talks.
- Производительность нейронных сетей
- Нейронные сети и информация. Архивировано 9 июля 2009 г. в Wayback Machine.
- Сандерсон Дж. (5 октября 2017 г.). «Но что такое нейронная сеть?» . 3Синий1Коричневый . Архивировано из оригинала 7 ноября 2021 года — на YouTube .
Примечания [ править ]
- ↑ Для управления мероприятием « Без рук по всей Америке » 1995 года потребовалось «всего несколько человек».
Ссылки [ править ]
- ^ Хардести Л. (14 апреля 2017 г.). «Объяснение: нейронные сети» . Пресс-служба Массачусетского технологического института. Архивировано из оригинала 18 марта 2024 года . Проверено 2 июня 2022 г.
- ^ Ян З, Ян З (2014). Комплексная биомедицинская физика . Каролинский институт, Стокгольм, Швеция: Elsevier. п. 1. ISBN 978-0-444-53633-4 . Архивировано из оригинала 28 июля 2022 года . Проверено 28 июля 2022 г.
- ^ Епископ К.М. (17 августа 2006 г.). Распознавание образов и машинное обучение . Нью-Йорк: Спрингер. ISBN 978-0-387-31073-2 .
- ↑ Перейти обратно: Перейти обратно: а б Вапник В.Н., Вапник В.Н. (1998). Природа статистической теории обучения (Исправленное 2-е издание). Нью-Йорк Берлин Гейдельберг: Springer. ISBN 978-0-387-94559-0 .
- ↑ Перейти обратно: Перейти обратно: а б Ян Гудфеллоу, Йошуа Бенджио и Аарон Курвиль (2016). Глубокое обучение . МТИ Пресс. Архивировано из оригинала 16 апреля 2016 года . Проверено 1 июня 2016 г.
- ^ Ферри К., Кайзер С. (2019). Нейронные сети для детей . Справочники. ISBN 978-1-4926-7120-6 .
- ^ Мэнсфилд Мерриман, «Список работ, касающихся метода наименьших квадратов»
- ^ Стиглер С.М. (1981). «Гаусс и изобретение метода наименьших квадратов» . Энн. Стат . 9 (3): 465–474. дои : 10.1214/aos/1176345451 .
- ^ Бретчер О (1995). Линейная алгебра с приложениями (3-е изд.). Река Аппер-Седл, Нью-Джерси: Прентис-Холл.
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л Шмидхубер Дж (2022). «Аннотированная история современного искусственного интеллекта и глубокого обучения». arXiv : 2212.11279 [ cs.NE ].
- ^ Стиглер С.М. (1986). История статистики: измерение неопределенности до 1900 года . Кембридж: Гарвард. ISBN 0-674-40340-1 .
- ^ Маккалок В., Уолтер Питтс (1943). «Логическое исчисление идей, имманентных нервной деятельности». Вестник математической биофизики . 5 (4): 115–133. дои : 10.1007/BF02478259 .
- ^ Клини С. (1956). «Представление событий в нервных сетях и конечных автоматах» . Анналы математических исследований . № 34. Издательство Принстонского университета. стр. 3–41. Архивировано из оригинала 19 мая 2024 года . Проверено 17 июня 2017 г.
- ^ Хебб Д. (1949). Организация поведения . Нью-Йорк: Уайли. ISBN 978-1-135-63190-1 .
- ^ Фарли Б., В.А. Кларк (1954). «Моделирование самоорганизующихся систем с помощью цифрового компьютера». IRE Транзакции по теории информации . 4 (4): 76–84. дои : 10.1109/TIT.1954.1057468 .
- ^ Рочестер Н., Дж. Х. Холланд, Л. Х. Хабит и В. Л. Дуда (1956). «Испытания теории сборки клеток действия мозга с использованием большого цифрового компьютера». IRE Транзакции по теории информации . 2 (3): 80–93. дои : 10.1109/TIT.1956.1056810 .
- ^ Хайкин (2008) Нейронные сети и обучающиеся машины, 3-е издание
- ^ Розенблатт Ф (1958). «Перцептрон: вероятностная модель хранения и организации информации в мозге». Психологический обзор . 65 (6): 386–408. CiteSeerX 10.1.1.588.3775 . дои : 10.1037/h0042519 . ПМИД 13602029 . S2CID 12781225 .
- ^ Вербос П (1975). За пределами регрессии: новые инструменты прогнозирования и анализа в поведенческих науках .
- ^ Розенблатт Ф (1957). «Персептрон — воспринимающий и распознающий автомат». Отчет 85-460-1 . Корнеллская авиационная лаборатория.
- ^ Олазаран М (1996). «Социологическое исследование официальной истории спора о перцептронах». Социальные исследования науки . 26 (3): 611–659. дои : 10.1177/030631296026003005 . JSTOR 285702 . S2CID 16786738 .
- ↑ Перейти обратно: Перейти обратно: а б Рассел, Стюарт, Норвиг, Питер (2010). Искусственный интеллект: современный подход (PDF) (3-е изд.). Соединенные Штаты Америки: Pearson Education. стр. 16–28. ISBN 978-0-13-604259-4 .
- ^ Минский М, Паперт С (1969). Перцептроны: введение в вычислительную геометрию . МТИ Пресс. ISBN 978-0-262-63022-1 .
- ↑ Перейти обратно: Перейти обратно: а б Рассел С.Дж., Норвиг П. (2021). Искусственный интеллект: современный подход . Серия Пирсона по искусственному интеллекту. Минг-Вэй Чанг, Джейкоб Девлин, Анка Драган, Дэвид Форсайт, Ян Гудфеллоу, Джитендра Малик, Викаш Мансингка, Джудея Перл, Майкл Дж. Вулдридж (4-е изд.). Хобокен, Нью-Джерси: Пирсон. ISBN 978-0-13-461099-3 .
- ^ Джакалья, врач общей практики (2 ноября 2022 г.). Заставить вещи думать . Холлоуэй. ISBN 978-1-952120-41-1 . Архивировано из оригинала 9 декабря 2023 года . Проверено 29 декабря 2023 г.
- ↑ Перейти обратно: Перейти обратно: а б с Шмидхубер Дж (2015). «Глубокое обучение в нейронных сетях: обзор». Нейронные сети . 61 : 85–117. arXiv : 1404.7828 . дои : 10.1016/j.neunet.2014.09.003 . ПМИД 25462637 . S2CID 11715509 .
- ^ Ивахненко А.Г. (1973). Кибернетические предсказывающие устройства . Информационная корпорация CCM.
- ^ Ивахненко А.Г., Лапа В.Г. (1967). Кибернетика и методы прогнозирования . Американский паб Elsevier. Ко.
- ^ Роббинс Х. , Монро С. (1951). «Метод стохастической аппроксимации» . Анналы математической статистики . 22 (3): 400. дои : 10.1214/aoms/1177729586 .
- ^ Амари С (1967). «Теория адаптивного классификатора шаблонов». IEEE-транзакции . ЕС (16): 279–307.
- ↑ Перейти обратно: Перейти обратно: а б Шмидхубер Дж (2022). «Аннотированная история современного искусственного интеллекта и глубокого обучения». arXiv : 2212.11279 [ cs.NE ].
- ↑ Перейти обратно: Перейти обратно: а б Кохонен Т., Хонкела Т. (2007). «Сеть Кохонена» . Схоларпедия . 2 (1): 1568. Бибкод : 2007SchpJ...2.1568K . doi : 10.4249/scholarpedia.1568 .
- ^ Кохонен Т. (1982). «Самоорганизованное формирование топологически правильных карт признаков». Биологическая кибернетика . 43 (1): 59–69. дои : 10.1007/bf00337288 . S2CID 206775459 .
- ^ Фон дер Мальсбург С (1973). «Самоорганизация ориентационно-чувствительных клеток в полосатой коре». Кибернетик . 14 (2): 85–100. дои : 10.1007/bf00288907 . ПМИД 4786750 . S2CID 3351573 .
- ^ Фукусима К (1980). «Неокогнитрон: самоорганизующаяся модель нейронной сети для механизма распознавания образов, на который не влияет сдвиг положения» (PDF) . Биологическая кибернетика . 36 (4): 193–202. дои : 10.1007/BF00344251 . ПМИД 7370364 . S2CID 206775608 . Архивировано (PDF) из оригинала 3 июня 2014 года . Проверено 16 ноября 2013 г.
- ^ Фукусима К (1969 г.). «Визуальное извлечение признаков с помощью многослойной сети аналоговых пороговых элементов». Транзакции IEEE по системным наукам и кибернетике . 5 (4): 322–333. дои : 10.1109/TSSC.1969.300225 .
- ^ Рамачандран П., Баррет З., Куок В.Л. (16 октября 2017 г.). «Поиск функций активации». arXiv : 1710.05941 [ cs.NE ].
- ^ Лейбниц Г.В. (1920). Ранние математические рукописи Лейбница: перевод с латинских текстов, опубликованных Карлом Иммануэлем Герхардтом с критическими и историческими примечаниями (Лейбниц опубликовал цепное правило в мемуарах 1676 года) . Издательство «Открытый суд». ISBN 978-0-598-81846-1 . Архивировано из оригинала 19 мая 2024 года . Проверено 1 апреля 2023 г.
- ^ Линнаинмаа С (1970). Представление совокупной ошибки округления алгоритма в виде разложения Тейлора локальных ошибок округления (Мастерс) (на финском языке). Университет Хельсинки. стр. 6–7.
- ^ Линнаинмаа С (1976). «Разложение Тейлора накопленной ошибки округления». БИТ Численная математика . 16 (2): 146–160. дои : 10.1007/bf01931367 . S2CID 122357351 .
- ^ Гриванк А. (2012). «Кто изобрел обратный способ дифференциации?». Истории оптимизации . Documenta Matematica, Дополнительный том ISMP. стр. 389–400. S2CID 15568746 .
- ^ Гриванк А., Вальтер А. (2008). Оценка производных: принципы и методы алгоритмического дифференцирования, второе издание . СИАМ. ISBN 978-0-89871-776-1 .
- ^ Розенблатт Ф (1962). Принципы нейродинамики . Спартан, Нью-Йорк.
- ^ Келли Х.Дж. (1960). «Градиентная теория оптимальных траекторий полета». Журнал АРС . 30 (10): 947–954. дои : 10.2514/8.5282 .
- ^ «Градиентный метод оптимизации многоэтапных процессов распределения». Труды Гарвардского университета. Симпозиум по цифровым вычислительным машинам и их приложениям . Апрель 1961 года.
- ↑ Перейти обратно: Перейти обратно: а б с Шмидхубер Дж (2015). «Глубокое обучение» . Схоларпедия . 10 (11): 85–117. Бибкод : 2015SchpJ..1032832S . doi : 10.4249/scholarpedia.32832 .
- ^ Дрейфус С.Е. (1 сентября 1990 г.). «Искусственные нейронные сети, обратное распространение ошибки и процедура градиента Келли-Брайсона». Журнал руководства, контроля и динамики . 13 (5): 926–928. Бибкод : 1990JGCD...13..926D . дои : 10.2514/3.25422 . ISSN 0731-5090 .
- ^ Мизутани Э., Дрейфус С. , Нишио К. (2000). «О выводе обратного распространения ошибки MLP из формулы градиента оптимального управления Келли-Брайсона и ее применении». Материалы Международной совместной конференции IEEE-INNS-ENNS по нейронным сетям. IJCNN 2000. Нейронные вычисления: новые вызовы и перспективы нового тысячелетия . IEEE. С. 167–172 т.2. дои : 10.1109/ijcnn.2000.857892 . ISBN 0-7695-0619-4 . S2CID 351146 .
- ^ Дрейфус С. (1973). «Вычислительное решение задач оптимального управления с запаздыванием». Транзакции IEEE при автоматическом управлении . 18 (4): 383–385. дои : 10.1109/tac.1973.1100330 .
- ^ Вербос П (1982). «Применение достижений нелинейного анализа чувствительности» (PDF) . Системное моделирование и оптимизация . Спрингер. стр. 762–770. Архивировано (PDF) из оригинала 14 апреля 2016 г. Проверено 2 июля 2017 г.
- ^ Дэвид Э. Румельхарт, Джеффри Э. Хинтон и Рональд Дж. Уильямс, « Изучение представлений с помощью ошибок обратного распространения. Архивировано 8 марта 2021 года в Wayback Machine », Nature , 323, страницы 533–536, 1986.
- ^ Кисть С.Г. (1967). «История модели Ленца-Изинга». Обзоры современной физики . 39 (4): 883–893. Бибкод : 1967РвМП...39..883Б . дои : 10.1103/RevModPhys.39.883 .
- ^ Амари С.И. (1972). «Обучение шаблонам и последовательностям шаблонов с помощью самоорганизующихся сетей пороговых элементов». IEEE-транзакции . С (21): 1197–1206.
- ^ Барт П.Ф. (1981). Кооперативность и переходное поведение больших нейронных сетей (дипломная работа). Берлингтон: Университет Вермонта. OCLC 8231704 .
- ^ Кризан Дж., Барт П. , Глассер М. (1983). «Точные фазовые переходы для модели Изинга на замкнутом дереве Кэли». Физика . 119А . Издательство Северной Голландии: 230–242. дои : 10.1016/0378-4371(83)90157-7 .
- ^ Глассер М., Голдберг М. (1983), «Модель Изинга на замкнутом дереве Кэли», Physica , 117A (2–3): 670–672, Бибкод : 1983PhyA..117..670G , doi : 10.1016/0378-4371 (83)90138-3
- ^ Хопфилд Джей-Джей (1982). «Нейронные сети и физические системы с возникающими коллективными вычислительными способностями» . Труды Национальной академии наук . 79 (8): 2554–2558. Бибкод : 1982PNAS...79.2554H . дои : 10.1073/pnas.79.8.2554 . ПМЦ 346238 . ПМИД 6953413 .
- ^ Вайбель А. (декабрь 1987 г.). Распознавание фонем с использованием нейронных сетей с задержкой . Заседание Института инженеров по электротехнике, информатике и связи (IEICE). Токио, Япония.
- ^ Александр Вайбель и др., Распознавание фонем с использованием нейронных сетей с задержкой. Архивировано 25 февраля 2021 г. в Wayback Machine IEEE Transactions on Acoustics, Speech and Signal Processing, Том 37, № 3, стр. 328. – 339, март 1989 г.
- ^ Чжан В (1988). «Сдвиг-инвариантная нейронная сеть распознавания образов и ее оптическая архитектура» . Материалы ежегодной конференции Японского общества прикладной физики . Архивировано из оригинала 23 июня 2020 года . Проверено 12 апреля 2023 г.
- ^ Чжан В (1990). «Модель параллельной распределенной обработки с локальными пространственно-инвариантными соединениями и ее оптическая архитектура» . Прикладная оптика . 29 (32): 4790–7. Бибкод : 1990ApOpt..29.4790Z . дои : 10.1364/AO.29.004790 . ПМИД 20577468 . Архивировано из оригинала 6 февраля 2017 года . Проверено 12 апреля 2023 г.
- ^ ЛеКун и др. , «Обратное распространение ошибки, примененное к распознаванию рукописного почтового индекса», Neural Computation , 1, стр. 541–551, 1989.
- ^ Дж. Венг, Н. Ахуджа и Т. С. Хуанг, « Кресцептрон: самоорганизующаяся нейронная сеть, которая растет адаптивно. Архивировано 21 сентября 2017 г. в Wayback Machine », Proc. Международная совместная конференция по нейронным сетям , Балтимор, Мэриленд, том I, стр. 576–581, июнь 1992 г.
- ^ Дж. Венг, Н. Ахуджа и Т. С. Хуанг, « Обучение распознаванию и сегментации трехмерных объектов из двумерных изображений. Архивировано 21 сентября 2017 г. в Wayback Machine », Proc. 4-я Международная конференция. Computer Vision , Берлин, Германия, стр. 121–128, май 1993 г.
- ^ Дж. Венг, Н. Ахуджа и Т. С. Хуанг, « Обучение распознаванию и сегментации с использованием кресцептрона. Архивировано 25 января 2021 года в Wayback Machine », International Journal of Computer Vision , vol. 25, нет. 2, стр. 105–139, ноябрь 1997 г.
- ^ ЛеКун И, Леон Ботту, Йошуа Бенджио, Патрик Хаффнер (1998). «Градиентное обучение, применяемое для распознавания документов» (PDF) . Труды IEEE . 86 (11): 2278–2324. CiteSeerX 10.1.1.32.9552 . дои : 10.1109/5.726791 . S2CID 14542261 . Архивировано (PDF) из оригинала 15 декабря 2017 года . Проверено 7 октября 2016 г.
- ^ Цянь, Нин и Терренс Дж. Сейновски. «Предсказание вторичной структуры глобулярных белков с использованием моделей нейронных сетей». Журнал молекулярной биологии 202, вып. 4 (1988): 865-884.
- ^ Бор, Хенрик, Якоб Бор, Сёрен Брунак, Родни М. Дж. Коттерилл, Бенни Лаутруп, Лейф Норсков, Оле Х. Олсен и Штеффен Б. Петерсен. «Вторичная структура белка и гомология нейронных сетей. α-спирали в родопсине». Письма ФЭБС 241, (1988): 223-228.
- ^ Рост, Буркхард и Крис Сандер. «Предсказание вторичной структуры белка с точностью более 70%». Журнал молекулярной биологии 232, вып. 2 (1993): 584-599.
- ↑ Перейти обратно: Перейти обратно: а б С. Хохрейтер, « Исследования динамических нейронных сетей. Архивировано 6 марта 2015 г. в Wayback Machine », Дипломная работа. Институт компьютерных наук Технического университета Мюнхен. Советник: Дж. Шмидхубер , 1991 г.
- ^ Хохрайтер С. и др. (15 января 2001 г.). «Градиентный поток в рекуррентных сетях: сложность изучения долгосрочных зависимостей» . Колен Дж. Ф., Кремер СК (ред.). Полевое руководство по динамическим рекуррентным сетям . Джон Уайли и сыновья. ISBN 978-0-7803-5369-5 . Архивировано из оригинала 19 мая 2024 года . Проверено 26 июня 2017 г.
- ^ Шмидхубер Дж (1991). «Возможность реализовать любопытство и скуку в нейронных контроллерах для построения моделей». Учеб. САБ'1991 . MIT Press/Брэдфорд Букс. стр. 222–227.
- ^ Шмидхубер Дж (2010). «Формальная теория творчества, веселья и внутренней мотивации (1990–2010)». Транзакции IEEE по автономному умственному развитию . 2 (3): 230–247. дои : 10.1109/TAMD.2010.2056368 . S2CID 234198 .
- ^ Шмидхубер Дж (2020). «Генераторно-состязательные сети представляют собой особые случаи искусственного любопытства (1990), а также тесно связаны с минимизацией предсказуемости (1991)». Нейронные сети . 127 : 58–66. arXiv : 1906.04493 . doi : 10.1016/j.neunet.2020.04.008 . ПМИД 32334341 . S2CID 216056336 .
- ↑ Перейти обратно: Перейти обратно: а б Шмидхубер Дж (1992). «Изучение сложных, расширенных последовательностей с использованием принципа сжатия истории» (PDF) . Нейронные вычисления . 4 (2): 234–242. дои : 10.1162/neco.1992.4.2.234 . S2CID 18271205 . [ постоянная мертвая ссылка ]
- ^ Шмидхубер Дж. (1 ноября 1992 г.). «Научимся контролировать быстрые воспоминания: альтернатива повторяющимся сетям». Нейронные вычисления . 4 (1): 131–139. дои : 10.1162/neco.1992.4.1.131 . S2CID 16683347 .
- ^ Шлаг I, Ири К., Шмидхубер Дж (2021). «Линейные трансформаторы — тайно быстрые программисты веса». ICML 2021 . Спрингер. стр. 9355–9366.
- ^ Чоромански К., Лихошерстов В., Дохан Д., Сонг Х., Гане А., Сарлос Т. и др. (2020). «Переосмысление внимания с исполнителями». arXiv : 2009.14794 [ cs.CL ].
- ^ Шмидхубер Дж (1993). «Уменьшение соотношения между сложностью обучения и количеством изменяющихся во времени переменных в полностью рекуррентных сетях». ИКАНН, 1993 год . Спрингер. стр. 460–463.
- ^ Мид, Калифорния , Исмаил М. (8 мая 1989 г.). Аналоговая реализация нейронных систем СБИС (PDF) . Международная серия Kluwer по инженерным наукам и информатике. Том. 80. Норвелл, Массачусетс: Kluwer Academic Publishers . дои : 10.1007/978-1-4613-1639-8 . ISBN 978-1-4613-1639-8 . Архивировано (PDF) из оригинала 6 ноября 2019 года . Проверено 24 января 2020 г.
- ^ Домингос П. (22 сентября 2015 г.). «глава 4». Главный алгоритм: как поиски совершенной обучающейся машины изменят наш мир . Основные книги . ISBN 978-0-465-06570-7 .
- ^ Хохрайтер С., Шмидхубер Дж (1 ноября 1997 г.). «Долгая кратковременная память». Нейронные вычисления . 9 (8): 1735–1780. дои : 10.1162/neco.1997.9.8.1735 . ISSN 0899-7667 . ПМИД 9377276 . S2CID 1915014 .
- ^ Шмидхубер Дж (2015). «Глубокое обучение в нейронных сетях: обзор». Нейронные сети . 61 : 85–117. arXiv : 1404.7828 . дои : 10.1016/j.neunet.2014.09.003 . ПМИД 25462637 . S2CID 11715509 .
- ^ Герс Ф., Шмидхубер Дж., Камминс Ф. (1999). «Учимся забывать: постоянное предсказание с помощью LSTM». 9-я Международная конференция по искусственным нейронным сетям: ICANN '99 . Том. 1999. стр. 850–855. дои : 10.1049/cp:19991218 . ISBN 0-85296-721-7 .
- ^ Смоленский П (1986). «Обработка информации в динамических системах: основы теории гармонии». . В DE Rumelhart, JL McClelland, PDP Research Group (ред.). Параллельная распределенная обработка: исследования микроструктуры познания . Том. 1. стр. 194–281 . ISBN 978-0-262-68053-0 .
- ^ Нг А, Дин Дж (2012). «Создание функций высокого уровня с использованием крупномасштабного обучения без учителя». arXiv : 1112.6209 [ cs.LG ].
- ^ Хинтон Дж.Э. , Осиндеро С., Тех Ю. (2006). «Алгоритм быстрого обучения для сетей глубокого доверия» (PDF ) Нейронные вычисления . 18 (7): 1527–1554. CiteSeerX 10.1.1.76.1541 . дои : 10.1162/neco.2006.18.7.1527 . ПМИД 16764513 . S2CID 2309950 . Архивировано (PDF) 23 декабря. из оригинала Получено 13 декабря.
- ^ Фукусима К (1980). «Неокогнитрон: самоорганизующаяся модель нейронной сети для механизма распознавания образов, на который не влияет сдвиг положения». Биологическая кибернетика . 36 (4): 93–202. дои : 10.1007/BF00344251 . ПМИД 7370364 . S2CID 206775608 .
- ^ Ризенхубер М., Поджо Т. (1999). «Иерархические модели распознавания объектов в коре». Природная неврология . 2 (11): 1019–1025. дои : 10.1038/14819 . ПМИД 10526343 . S2CID 8920227 .
- ^ Ян Дж. Дж., Пикетт М.Д., Ли К.М., Ольберг Д.А., Стюарт Д.Р., Уильямс Р.С. (2008). «Мемристивный механизм переключения для наноустройств металл/оксид/металл». Нат. Нанотехнологии. 3 (7): 429–433. дои : 10.1038/nnano.2008.160 . ПМИД 18654568 .
- ^ Струков Д.Б., Снайдер Г.С., Стюарт Д.Р., Уильямс Р.С. (2008). «Найден пропавший мемристор». Природа . 453 (7191): 80–83. Бибкод : 2008Natur.453...80S . дои : 10.1038/nature06932 . ПМИД 18451858 . S2CID 4367148 .
- ^ Чирешан, Д.С., Мейер У, Гамбарделла Л.М., Шмидхубер Дж. (21 сентября 2010 г.). «Глубокие, большие и простые нейронные сети для распознавания рукописных цифр». Нейронные вычисления . 22 (12): 3207–3220. arXiv : 1003.0358 . дои : 10.1162/neco_a_00052 . ISSN 0899-7667 . ПМИД 20858131 . S2CID 1918673 .
- ^ Доминик Шерер, Андреас К. Мюллер и Свен Бенке: « Оценка операций объединения в сверточных архитектурах для распознавания объектов. Архивировано 3 апреля 2018 г. на Wayback Machine », на 20-й Международной конференции по искусственным нейронным сетям (ICANN) , стр. 92–101. , 2010. дои : 10.1007/978-3-642-15825-4_10 .
- ^ Интервью Kurzweil AI, 2012 г. Архивировано 31 августа 2018 г. в Wayback Machine с Юргеном Шмидхубером о восьми соревнованиях, выигранных его командой глубокого обучения в 2009–2012 гг.
- ^ «Как глубокое обучение на основе биотехнологий продолжает побеждать в соревнованиях | KurzweilAI» . www.kurzweilai.net . Архивировано из оригинала 31 августа 2018 года . Проверено 16 июня 2017 г.
- ↑ Перейти обратно: Перейти обратно: а б Грейвс А., Шмидхубер Дж (2009). «Офлайн-распознавание рукописного текста с помощью многомерных рекуррентных нейронных сетей» (PDF) . Коллер Д., Шурманс Д., Бенджио Ю., Ботту Л. (ред.). Достижения в области нейронных систем обработки информации 21 (NIPS 2008) . Фонд систем нейронной обработки информации (NIPS). стр. 545–552. ISBN 978-1-60560-949-2 . Архивировано из оригинала 19 мая 2024 года . Проверено 3 июня 2022 г.
- ↑ Перейти обратно: Перейти обратно: а б Грейвс А., Ливицки М., Фернандес С., Бертолами Р., Бунке Х., Шмидхубер Дж. (май 2009 г.). «Новая коннекционистская система для неограниченного распознавания рукописного текста» (PDF) . Транзакции IEEE по анализу шаблонов и машинному интеллекту . 31 (5): 855–868. CiteSeerX 10.1.1.139.4502 . дои : 10.1109/tpami.2008.137 . ISSN 0162-8828 . ПМИД 19299860 . S2CID 14635907 . Архивировано (PDF) из оригинала 2 января 2014 года . Проверено 30 июля 2014 г.
- ^ Чиресан Д., Мейер У., Шмидхубер Дж. (июнь 2012 г.). «Многостолбцовые глубокие нейронные сети для классификации изображений». Конференция IEEE 2012 по компьютерному зрению и распознаванию образов . стр. 3642–3649. arXiv : 1202.2745 . Бибкод : 2012arXiv1202.2745C . CiteSeerX 10.1.1.300.3283 . дои : 10.1109/cvpr.2012.6248110 . ISBN 978-1-4673-1228-8 . S2CID 2161592 .
- ↑ Перейти обратно: Перейти обратно: а б Биллингс С.А. (2013). Идентификация нелинейных систем: методы NARMAX во временной, частотной и пространственно-временной областях . Уайли. ISBN 978-1-119-94359-4 .
- ↑ Перейти обратно: Перейти обратно: а б Гудфеллоу И., Пуже-Абади Дж., Мирза М., Сюй Б., Вард-Фарли Д., Озаир С. и др. (2014). Генеративно-состязательные сети (PDF) . Материалы Международной конференции по нейронным системам обработки информации (NIPS 2014). стр. 2672–2680. Архивировано (PDF) из оригинала 22 ноября 2019 г. Проверено 20 августа 2019 г.
- ^ «Готовьтесь, не паникуйте: синтетические медиа и дипфейки» . свидетель.орг. Архивировано из оригинала 2 декабря 2020 года . Проверено 25 ноября 2020 г.
- ^ «GAN 2.0: гиперреалистичный генератор лиц NVIDIA» . SyncedReview.com . 14 декабря 2018 года . Проверено 3 октября 2019 г.
- ^ Каррас Т., Айла Т., Лайне С., Лехтинен Дж. (1 октября 2017 г.). «Прогрессивное развитие GAN для повышения качества, стабильности и разнообразия». arXiv : 1710.10196 [ cs.NE ].
- ^ Шривастава Р.К., Грефф К., Шмидхубер Дж. (2 мая 2015 г.). «Дорожные сети». arXiv : 1505.00387 [ cs.LG ].
- ^ Шривастава Р.К., Грефф К., Шмидхубер Дж. (2015). «Обучение очень глубоких сетей» . Достижения в области нейронных систем обработки информации . 28 . Curran Associates, Inc.: 2377–2385. Архивировано из оригинала 11 августа 2020 года . Проверено 15 апреля 2023 г.
- ^ Хэ К., Чжан Х, Рен С., Сунь Дж. (2016). Глубокое остаточное обучение для распознавания изображений . Конференция IEEE 2016 по компьютерному зрению и распознаванию образов (CVPR) . Лас-Вегас, Невада, США: IEEE. стр. 770–778. arXiv : 1512.03385 . дои : 10.1109/CVPR.2016.90 . ISBN 978-1-4673-8851-1 . Архивировано из оригинала 12 апреля 2023 года . Проверено 15 апреля 2023 г.
- ^ Васвани А., Шазир Н., Пармар Н., Ушкорейт Дж., Джонс Л., Гомес А.Н. и др. (12 июня 2017 г.). «Внимание — это все, что вам нужно» arXiv : 1706.03762 [ cs.CL ].
- ^ Вольф Т., Дебют Л., Сан В., Шомон Дж., Деланг С., Мой А. и др. (2020). «Трансформеры: современная обработка естественного языка». Материалы конференции 2020 года по эмпирическим методам обработки естественного языка: системные демонстрации . стр. 38–45. doi : 10.18653/v1/2020.emnlp-demos.6 . S2CID 208117506 .
- ^ Он С (31 декабря 2021 г.). «Трансформатор в резюме» . Трансформатор в ЦВ . На пути к науке о данных. Архивировано из оригинала 16 апреля 2023 года . Проверено 12 апреля 2023 г.
- ^ [Рамезанпур, А.; Бим, Алабама; Чен, Дж. Х.; Машаги, А. Статистическая физика для медицинской диагностики: алгоритмы обучения, вывода и оптимизации. Диагностика 2020, 10, 972. ]
- ↑ Перейти обратно: Перейти обратно: а б Зелл А (2003). «глава 5.2». Моделирование нейроналера Netze [ Моделирование нейронных сетей ] (на немецком языке) (1-е изд.). Аддисон-Уэсли. ISBN 978-3-89319-554-1 . ОСЛК 249017987 .
- ^ Искусственный интеллект (3-е изд.). Паб Аддисон-Уэсли. Ко. 1992. ISBN. 0-201-53377-4 .
- ^ Аббод М.Ф. (2007). «Применение искусственного интеллекта для лечения урологического рака». Журнал урологии . 178 (4): 1150–1156. дои : 10.1016/j.juro.2007.05.122 . ПМИД 17698099 .
- ^ Доусон CW (1998). «Подход на основе искусственных нейронных сетей к моделированию стока осадков» . Журнал гидрологических наук . 43 (1): 47–66. Бибкод : 1998HydSJ..43...47D . дои : 10.1080/02626669809492102 .
- ^ «Словарь машинного обучения» . www.cse.unsw.edu.au. Архивировано из оригинала 26 августа 2018 года . Проверено 4 ноября 2009 г.
- ^ Чиресан Д., Ули Мейер, Джонатан Маски, Лука М. Гамбарделла, Юрген Шмидхубер (2011). «Гибкие, высокопроизводительные сверточные нейронные сети для классификации изображений» (PDF) . Материалы двадцать второй Международной совместной конференции по искусственному интеллекту, том второй . 2 : 1237–1242. Архивировано (PDF) из оригинала 5 апреля 2022 года . Проверено 7 июля 2022 г.
- ^ Зелл А (1994). сетей ( Моделирование нейронных на немецком языке) (1-е изд.). Эддисон Уэсли. п. 73. ИСБН 3-89319-554-8 .
- ^ Милянович М. (февраль – март 2012 г.). «Сравнительный анализ нейронных сетей с рекуррентным и конечным импульсным откликом в прогнозировании временных рядов» (PDF) . Индийский журнал компьютеров и техники . 3 (1). Архивировано (PDF) из оригинала 19 мая 2024 года . Проверено 21 августа 2019 г.
- ^ Лау С (10 июля 2017 г.). «Пошаговое руководство по сверточной нейронной сети – настройка гиперпараметров» . Середина . Архивировано из оригинала 4 февраля 2023 года . Проверено 23 августа 2019 г.
- ^ Келлехер Дж. Д., Мак Нами Б., Д'Арси А. (2020). «7-8». Основы машинного обучения для прогнозного анализа данных: алгоритмы, рабочие примеры и тематические исследования (2-е изд.). Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-36110-1 . OCLC 1162184998 .
- ^ Вэй Дж (26 апреля 2019 г.). «Забудьте о скорости обучения и потерях на распад». arXiv : 1905.00094 [ cs.LG ].
- ^ Ли Ю, Фу Ю, Ли Х, Чжан СВ (1 июня 2009 г.). «Улучшенный алгоритм обучения нейронной сети обратного распространения ошибки с самоадаптирующейся скоростью обучения». Международная конференция 2009 г. по вычислительному интеллекту и естественным вычислениям . Том. 1. С. 73–76. дои : 10.1109/CINC.2009.111 . ISBN 978-0-7695-3645-3 . S2CID 10557754 .
- ^ Хуан ГБ, Чжу Ци, Сью К.К. (2006). «Машина экстремального обучения: теория и приложения». Нейрокомпьютинг . 70 (1): 489–501. CiteSeerX 10.1.1.217.3692 . дои : 10.1016/j.neucom.2005.12.126 . S2CID 116858 .
- ^ Видроу Б. и др. (2013). «Алгоритм без поддержки: новый алгоритм обучения для многослойных нейронных сетей». Нейронные сети . 37 : 182–188. дои : 10.1016/j.neunet.2012.09.020 . ПМИД 23140797 .
- ^ Оливье Ю., Шарпиа Дж. (2015). «Обучение рекуррентных сетей без возврата». arXiv : 1507.07680 [ cs.NE ].
- ^ Хинтон Дж. Э. (2010). «Практическое руководство по обучению ограниченных машин Больцмана» . Тех. Реп. УТМЛ ТР 2010-003 . Архивировано из оригинала 9 мая 2021 года . Проверено 27 июня 2017 г.
- ^ Эссен. 2009. [ нужна полная цитата ]
- ^ Бернард Э (2021). Введение в машинное обучение . Шампанское: Вольфрам Медиа. п. 9. ISBN 978-1-57955-048-6 . Архивировано из оригинала 19 мая 2024 года . Проверено 22 марта 2023 г.
- ^ Бернард Э (2021). Введение в машинное обучение . Шампанское: Вольфрам Медиа. п. 12. ISBN 978-1-57955-048-6 . Архивировано из оригинала 19 мая 2024 года . Проверено 22 марта 2023 г.
- ^ Бернард Э (2021). Введение в машинное обучение . Wolfram Media Inc. с. 9. ISBN 978-1-57955-048-6 . Архивировано из оригинала 19 мая 2024 года . Проверено 28 июля 2022 г.
- ^ Ойха В.К., Авраам А., Снашель В. (1 апреля 2017 г.). «Метаэвристический дизайн нейронных сетей прямого распространения: обзор двух десятилетий исследований». Инженерные применения искусственного интеллекта . 60 : 97–116. arXiv : 1705.05584 . Бибкод : 2017arXiv170505584O . дои : 10.1016/j.engappai.2017.01.013 . S2CID 27910748 .
- ^ Доминик С., Дас Р., Уитли Д., Андерсон К. (июль 1991 г.). «Генетическое обучение с подкреплением для нейронных сетей» . IJCNN-91-Сиэтлская международная совместная конференция по нейронным сетям . IJCNN-91-Сиэтлская международная совместная конференция по нейронным сетям. Сиэтл, Вашингтон, США: IEEE. стр. 71–76. дои : 10.1109/IJCNN.1991.155315 . ISBN 0-7803-0164-1 .
- ^ Хоскинс Дж., Химмельблау, DM (1992). «Управление процессами с помощью искусственных нейронных сетей и обучение с подкреплением». Компьютеры и химическая инженерия . 16 (4): 241–251. дои : 10.1016/0098-1354(92)80045-Б .
- ^ Берцекас Д., Цициклис Дж. (1996). Нейродинамическое программирование . Афина Сайентифик. п. 512. ИСБН 978-1-886529-10-6 . Архивировано из оригинала 29 июня 2017 года . Проверено 17 июня 2017 г.
- ^ Секоманди Н (2000). «Сравнение алгоритмов нейродинамического программирования для задачи выбора маршрута транспортных средств со стохастическими требованиями». Компьютеры и исследования операций . 27 (11–12): 1201–1225. CiteSeerX 10.1.1.392.4034 . дои : 10.1016/S0305-0548(99)00146-X .
- ^ де Риго Д., Риццоли А.Е., Сончини-Сесса Р., Вебер Э., Зенеси П. (2001). «Нейродинамическое программирование для эффективного управления пластовыми сетями» . Материалы MODSIM 2001, Международного конгресса по моделированию и симуляции . MODSIM 2001, Международный конгресс по моделированию и симуляции. Канберра, Австралия: Общество моделирования и моделирования Австралии и Новой Зеландии. дои : 10.5281/zenodo.7481 . ISBN 0-86740-525-2 . Архивировано из оригинала 7 августа 2013 года . Проверено 29 июля 2013 г.
- ^ Дамас М., Салмерон М., Диас А., Ортега Дж., Прието А., Оливарес Г. (2000). «Генетические алгоритмы и нейродинамическое программирование: применение в сетях водоснабжения». Труды Конгресса 2000 года по эволюционным вычислениям . Конгресс 2000 г. по эволюционным вычислениям. Том. 1. Ла-Хойя, Калифорния, США: IEEE. стр. 7–14. дои : 10.1109/CEC.2000.870269 . ISBN 0-7803-6375-2 .
- ^ Дэн Дж., Феррис, MC (2008). «Нейродинамическое программирование для планирования фракционированной лучевой терапии». Оптимизация в медицине . Оптимизация Springer и ее приложения. Том. 12. С. 47–70. CiteSeerX 10.1.1.137.8288 . дои : 10.1007/978-0-387-73299-2_3 . ISBN 978-0-387-73298-5 .
- ^ Бозиновский, С. (1982). «Самообучающаяся система с использованием вторичного подкрепления». В Р. Траппле (ред.) Кибернетика и системные исследования: материалы шестого европейского совещания по кибернетике и системным исследованиям. Северная Голландия. стр. 397–402. ISBN 978-0-444-86488-8 .
- ^ Бозиновский, С. (2014) « Моделирование механизмов когнитивно-эмоционального взаимодействия в искусственных нейронных сетях, с 1981 г. Архивировано 23 марта 2019 г. в Wayback Machine ». Procedia Информатика с. 255-263
- ^ Божиновский С, Божиновская Л (2001). «Самообучающиеся агенты: коннекционистская теория эмоций, основанная на перекрестном оценочном суждении». Кибернетика и системы . 32 (6): 637–667. дои : 10.1080/01969720118145 . S2CID 8944741 .
- ^ «Искусственный интеллект может «развиваться» для решения проблем» . Наука | АААС . 10 января 2018 года. Архивировано из оригинала 9 декабря 2021 года . Проверено 7 февраля 2018 г.
- ^ Турчетти С. (2004), Стохастические модели нейронных сетей , Границы искусственного интеллекта и приложений: интеллектуальные инженерные системы, основанные на знаниях, том. 102, IOS Press, ISBN 978-1-58603-388-0
- ^ Жоспен Л.В., Лага Х., Буссаид Ф., Бунтин В., Беннамун М. (2022). «Практические байесовские нейронные сети — руководство для пользователей глубокого обучения». Журнал IEEE Computational Intelligence . Том. 17, нет. 2. С. 29–48. arXiv : 2007.06823 . дои : 10.1109/mci.2022.3155327 . ISSN 1556-603X . S2CID 220514248 .
- ^ де Риго Д., Кастеллетти А., Риццоли А.Е., Сончини-Сесса Р., Вебер Э. (январь 2005 г.). «Техника выборочного улучшения для усиления нейродинамического программирования в управлении сетями водных ресурсов» . У Павла Зитека (ред.). Материалы 16-го Всемирного конгресса IFAC – IFAC-PapersOnLine . 16-й Всемирный конгресс МФБ . Том. 16. Прага, Чехия: МФБ. стр. 7–12. дои : 10.3182/20050703-6-CZ-1902.02172 . hdl : 11311/255236 . ISBN 978-3-902661-75-3 . Архивировано из оригинала 26 апреля 2012 года . Проверено 30 декабря 2011 г.
- ^ Феррейра С (2006). «Проектирование нейронных сетей с использованием программирования экспрессии генов». В А. Абрахаме, Б. де Баеце, М. Кеппене, Б. Николае (ред.). Прикладные технологии мягких вычислений: проблема сложности (PDF) . Спрингер-Верлаг. стр. 517–536. Архивировано (PDF) из оригинала 19 декабря 2013 года . Проверено 8 октября 2012 года .
- ^ Да Ю., Сюрун Г. (июль 2005 г.). «Улучшенная ИНС на основе PSO с методом моделирования отжига» . В Т. Вильманне (ред.). Новые аспекты нейрокомпьютинга: 11-й Европейский симпозиум по искусственным нейронным сетям . Том. 63. Эльзевир. стр. 527–533. дои : 10.1016/j.neucom.2004.07.002 . Архивировано из оригинала 25 апреля 2012 года . Проверено 30 декабря 2011 г.
- ^ Ву Дж., Чен Э. (май 2009 г.). «Новый ансамбль непараметрической регрессии для прогнозирования осадков с использованием метода оптимизации роя частиц в сочетании с искусственной нейронной сетью» . В Ван Х., Шен Ю., Хуан Т., Цзэн З. (ред.). 6-й международный симпозиум по нейронным сетям, ISNN 2009 . Конспекты лекций по информатике. Том. 5553. Спрингер. стр. 49–58. дои : 10.1007/978-3-642-01513-7_6 . ISBN 978-3-642-01215-0 . Архивировано из оригинала 31 декабря 2014 года . Проверено 1 января 2012 г.
- ↑ Перейти обратно: Перейти обратно: а б Тин Цинь, Цзунхай Чен, Хайтао Чжан, Сифу Ли, Вэй Сян, Мин Ли (2004). «Алгоритм обучения CMAC на основе RLS» (PDF) . Нейронная обработка писем . 19 (1): 49–61. дои : 10.1023/B:NEPL.0000016847.18175.60 . S2CID 6233899 . Архивировано (PDF) из оригинала 14 апреля 2021 года . Проверено 30 января 2019 г.
- ^ Тин Цинь, Хайтао Чжан, Цзунхай Чен, Вэй Сян (2005). «Непрерывный CMAC-QRLS и его систолический массив» (PDF) . Нейронная обработка писем . 22 (1): 1–16. дои : 10.1007/s11063-004-2694-0 . S2CID 16095286 . Архивировано (PDF) из оригинала 18 ноября 2018 года . Проверено 30 января 2019 г.
- ^ Лекун Ю., Бозер Б., Денкер Дж.С., Хендерсон Д., Ховард Р.Э., Хаббард В. и др. (1989). «Обратное распространение ошибки, примененное к распознаванию рукописного почтового индекса». Нейронные вычисления . 1 (4): 541–551. дои : 10.1162/neco.1989.1.4.541 . S2CID 41312633 .
- ^ Янн ЛеКун (2016). Слайды по глубокому обучению в Интернете. Архивировано 23 апреля 2016 г. на Wayback Machine.
- ^ Хохрайтер С. , Шмидхубер Дж. (1 ноября 1997 г.). «Долгая кратковременная память». Нейронные вычисления . 9 (8): 1735–1780. дои : 10.1162/neco.1997.9.8.1735 . ISSN 0899-7667 . ПМИД 9377276 . S2CID 1915014 .
- ^ Сак Х., Старший А., Бофей Ф. (2014). «Архитектуры рекуррентных нейронных сетей с долгосрочной кратковременной памятью для крупномасштабного акустического моделирования» (PDF) . Архивировано из оригинала (PDF) 24 апреля 2018 года.
- ^ Ли X, Ву X (15 октября 2014 г.). «Построение глубоких рекуррентных нейронных сетей на основе долговременной памяти для распознавания речи с большим словарным запасом». arXiv : 1410.4281 [ cs.CL ].
- ^ Фань Ю, Цянь Ю, Се Ф, Сунг ФК (2014). «Синтез TTS с помощью двунаправленных рекуррентных нейронных сетей на основе LSTM» . Материалы ежегодной конференции Международной ассоциации речевой коммуникации Interspeech : 1964–1968 . Проверено 13 июня 2017 г.
- ^ Дзен Х, Сак Х (2015). «Однонаправленная рекуррентная нейронная сеть с долговременной краткосрочной памятью и рекуррентным выходным слоем для синтеза речи с малой задержкой» (PDF) . Google.com . ИКАССП. стр. 4470–4474. Архивировано (PDF) из оригинала 9 мая 2021 года . Проверено 27 июня 2017 г.
- ^ Фан Б, Ван Л, Сунг Ф.К., Се Л (2015). «Фотореалистичная говорящая голова с глубоким двунаправленным LSTM» (PDF) . Труды ICASSP . Архивировано (PDF) из оригинала 1 ноября 2017 г. Проверено 27 июня 2017 г.
- ^ Сильвер Д. , Хуберт Т., Шритвизер Дж., Антоноглу И., Лай М., Гез А. и др. (5 декабря 2017 г.). «Освоение шахмат и сёги путем самостоятельной игры с помощью общего алгоритма обучения с подкреплением». arXiv : 1712.01815 [ cs.AI ].
- ^ Пробст П., Булестей А.Л., Бишль Б. (26 февраля 2018 г.). «Настраиваемость: важность гиперпараметров алгоритмов машинного обучения». Дж. Мах. Учиться. Рез . 20 : 53:1–53:32. S2CID 88515435 .
- ^ Зоф Б., Le QV (4 ноября 2016 г.). «Поиск нейронной архитектуры с обучением с подкреплением». arXiv : 1611.01578 [ cs.LG ].
- ^ Хайфэн Цзинь, Цинцюань Сун, Ся Ху (2019). «Auto-keras: эффективная система поиска нейронной архитектуры» . Материалы 25-й Международной конференции ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных . АКМ. arXiv : 1806.10282 . Архивировано из оригинала 21 августа 2019 года . Проверено 21 августа 2019 г. - через autokeras.com.
- ^ Клаесен М., Де Мур Б. (2015). «Поиск гиперпараметров в машинном обучении». arXiv : 1502.02127 [ cs.LG ]. Бибкод : 2015arXiv150202127C
- ^ Эш Р. (1990). «Функциональное приближение». Справочник по прикладной математике (изд. Springer, США). Бостон, Массачусетс: Springer US. стр. 928–987. дои : 10.1007/978-1-4684-1423-3_17 . ISBN 978-1-4684-1423-3 .
- ^ Сарстедт М., Му Э (2019). «Регрессионный анализ» . Краткое руководство по исследованию рынка . Тексты Спрингера по бизнесу и экономике. Шпрингер Берлин Гейдельберг. стр. 209–256. дои : 10.1007/978-3-662-56707-4_7 . ISBN 978-3-662-56706-7 . S2CID 240396965 . Архивировано из оригинала 20 марта 2023 года . Проверено 20 марта 2023 г.
- ^ Тянь Дж., Тан Ю., Сунь С., Цзэн Дж., Цзинь Ю. (декабрь 2016 г.). «Самоадаптивная аппроксимация пригодности на основе сходства для эволюционной оптимизации» . Серия симпозиумов IEEE 2016 по вычислительному интеллекту (SSCI) . стр. 1–8. дои : 10.1109/SSCI.2016.7850209 . ISBN 978-1-5090-4240-1 . S2CID 14948018 . Архивировано из оригинала 19 мая 2024 года . Проверено 22 марта 2023 г.
- ^ Алалул В.С., Куреши А.Х. (2019). «Обработка данных с использованием искусственных нейронных сетей» . Динамическая ассимиляция данных – преодоление неопределенностей . doi : 10.5772/intechopen.91935 . ISBN 978-1-83968-083-0 . S2CID 219735060 . Архивировано из оригинала 20 марта 2023 года . Проверено 20 марта 2023 г.
- ^ Пал М., Рой Р., Басу Дж., Бепари М.С. (2013). «Слепое разделение источников: обзор и анализ» . Международная конференция Oriental COCOSDA 2013 года проводится совместно с Конференцией 2013 года по исследованию и оценке разговорного языка в Азии (O-COCOSDA/CASLRE) . IEEE. стр. 1–5. дои : 10.1109/ICSDA.2013.6709849 . ISBN 978-1-4799-2378-6 . S2CID 37566823 . Архивировано из оригинала 20 марта 2023 года . Проверено 20 марта 2023 г.
- ^ Зиссис Д (октябрь 2015 г.). «Облачная архитектура, способная воспринимать и прогнозировать поведение нескольких судов» . Прикладные мягкие вычисления . 35 : 652–661. дои : 10.1016/j.asoc.2015.07.002 . Архивировано из оригинала 26 июля 2020 года . Проверено 18 июля 2019 г.
- ^ Сенгупта Н., Сахидулла, Мэриленд, Саха, Гутам (август 2016 г.). «Классификация звуков легких с использованием кепстральных статистических характеристик». Компьютеры в биологии и медицине . 75 (1): 118–129. doi : 10.1016/j.compbiomed.2016.05.013 . ПМИД 27286184 .
- ^ Чой, Кристофер Б. и др. « 3d-r2n2: унифицированный подход к реконструкции трехмерных объектов с одним и несколькими изображениями. Архивировано 26 июля 2020 года в Wayback Machine ». Европейская конференция по компьютерному зрению. Спрингер, Чам, 2016 г.
- ^ Турек, Фред Д. (март 2007 г.). «Введение в нейросетевое машинное зрение» . Проектирование систем технического зрения . 12 (3). Архивировано из оригинала 16 мая 2013 года . Проверено 5 марта 2013 г.
- ^ Майтра Д.С., Бхаттачарья У, Паруи С.К. (август 2015 г.). «Общий подход на основе CNN к распознаванию рукописных символов в нескольких сценариях» . 2015 13-я Международная конференция по анализу и распознаванию документов (ICDAR) . стр. 1021–1025. дои : 10.1109/ICDAR.2015.7333916 . ISBN 978-1-4799-1805-8 . S2CID 25739012 . Архивировано из оригинала 16 октября 2023 года . Проверено 18 марта 2021 г.
- ^ Гесслер Дж. (август 2021 г.). «Датчик для анализа пищевых продуктов с применением импедансной спектроскопии и искусственных нейронных сетей» . РиуНет УПВ (1): 8–12. Архивировано из оригинала 21 октября 2021 года . Проверено 21 октября 2021 г.
- ^ Френч Дж (2016). «CAPM путешественника во времени». Журнал инвестиционных аналитиков . 46 (2): 81–96. дои : 10.1080/10293523.2016.1255469 . S2CID 157962452 .
- ^ Роман Михайлович Балабин, Екатерина Ивановна Ломакина (2009). «Нейросетевой подход к данным квантовой химии: точное предсказание энергий теории функционала плотности». Дж. Хим. Физ. 131 (7): 074104. Бибкод : 2009JChPh.131g4104B . дои : 10.1063/1.3206326 . ПМИД 19708729 .
- ^ Сильвер Д. и др. (2016). «Освоение игры в го с помощью глубоких нейронных сетей и поиска по дереву» (PDF) . Природа . 529 (7587): 484–489. Бибкод : 2016Natur.529..484S . дои : 10.1038/nature16961 . ПМИД 26819042 . S2CID 515925 . Архивировано (PDF) из оригинала 23 ноября 2018 г. Проверено 31 января 2019 г.
- ^ Пасик А. (27 марта 2023 г.). «Глоссарий искусственного интеллекта: объяснение нейронных сетей и других терминов» . Нью-Йорк Таймс . ISSN 0362-4331 . Архивировано из оригинала 1 сентября 2023 года . Проверено 22 апреля 2023 г.
- ^ Шехнер С. (15 июня 2017 г.). «Facebook усиливает искусственный интеллект для блокирования террористической пропаганды» . Уолл Стрит Джорнал . ISSN 0099-9660 . Архивировано из оригинала 19 мая 2024 года . Проверено 16 июня 2017 г.
- ^ Ганесан Н (2010). «Применение нейронных сетей в диагностике онкологических заболеваний с использованием демографических данных» . Международный журнал компьютерных приложений . 1 (26): 81–97. Бибкод : 2010IJCA....1z..81G . дои : 10.5120/476-783 .
- ^ Боттачи Л. (1997). «Искусственные нейронные сети, применяемые для прогнозирования результатов лечения пациентов с колоректальным раком в отдельных учреждениях» (PDF) . Ланцет . 350 (9076). Ланцет: 469–72. дои : 10.1016/S0140-6736(96)11196-X . ПМИД 9274582 . S2CID 18182063 . Архивировано из оригинала (PDF) 23 ноября 2018 года . Проверено 2 мая 2012 г.
- ^ Ализаде Э., Лайонс С.М., Касл Дж.М., Прасад А. (2016). «Измерение систематических изменений формы инвазивных раковых клеток с использованием моментов Цернике» . Интегративная биология . 8 (11): 1183–1193. дои : 10.1039/C6IB00100A . ПМИД 27735002 . Архивировано из оригинала 19 мая 2024 года . Проверено 28 марта 2017 г.
- ^ Лайонс С (2016). «Изменения формы клеток коррелируют с метастатическим потенциалом у мышей» . Биология Открытая . 5 (3): 289–299. дои : 10.1242/bio.013409 . ПМЦ 4810736 . ПМИД 26873952 .
- ^ Набиан М.А., Мейдани Х. (28 августа 2017 г.). «Глубокое обучение для ускоренного анализа надежности инфраструктурных сетей». Компьютерное гражданское и инфраструктурное проектирование . 33 (6): 443–458. arXiv : 1708.08551 . Бибкод : 2017arXiv170808551N . дои : 10.1111/mice.12359 . S2CID 36661983 .
- ^ Набиан М.А., Мейдани Х. (2018). «Ускорение стохастической оценки связности транспортных сетей после землетрясения с помощью суррогатов на основе машинного обучения» . 97-е ежегодное собрание Совета по транспортным исследованиям . Архивировано из оригинала 9 марта 2018 года . Проверено 14 марта 2018 г.
- ^ Диас Э., Бротонс В., Томас Р. (сентябрь 2018 г.). «Использование искусственных нейронных сетей для прогнозирования трехмерной упругой осадки фундаментов на грунтах с наклонными коренными породами» . Почвы и фундаменты . 58 (6): 1414–1422. Бибкод : 2018SoFou..58.1414D . дои : 10.1016/j.sandf.2018.08.001 . hdl : 10045/81208 . ISSN 0038-0806 .
- ^ Тайбиян А., Мохаммад Т.А., Газали А.Х., Машохор С. «Искусственная нейронная сеть для моделирования осадков и стоков» . Пертаника Журнал науки и технологий . 24 (2): 319–330. Архивировано из оригинала 17 мая 2023 года . Проверено 17 мая 2023 г.
- ^ Говиндараджу РС (1 апреля 2000 г.). «Искусственные нейронные сети в гидрологии. I: Предварительные концепции». Журнал гидрологической техники . 5 (2): 115–123. дои : 10.1061/(ASCE)1084-0699(2000)5:2(115) .
- ^ Говиндараджу РС (1 апреля 2000 г.). «Искусственные нейронные сети в гидрологии. II: Гидрологические приложения». Журнал гидрологической техники . 5 (2): 124–137. дои : 10.1061/(ASCE)1084-0699(2000)5:2(124) .
- ^ Перес DJ, Юппа С, Кавалларо Л, Кансельер А, Фоти Е (1 октября 2015 г.). «Значительное расширение рекордов высоты волн с помощью нейронных сетей и повторного анализа данных о ветре». Моделирование океана . 94 : 128–140. Бибкод : 2015OcMod..94..128P . дои : 10.1016/j.ocemod.2015.08.002 .
- ^ Дваракиш Г.С., Ракшит С., Натесан У (2013). «Обзор применения нейронных сетей в прибрежной инженерии» . Искусственные интеллектуальные системы и машинное обучение . 5 (7): 324–331. Архивировано из оригинала 15 августа 2017 года . Проверено 5 июля 2017 г.
- ^ Эрмини Л., Катани Ф., Касальи Н. (1 марта 2005 г.). «Искусственные нейронные сети применяются для оценки предрасположенности к оползням». Геоморфология . Геоморфологическая опасность и антропогенное воздействие в горных условиях. 66 (1): 327–343. Бибкод : 2005Geomo..66..327E . дои : 10.1016/j.geomorph.2004.09.025 .
- ^ Никс Р., Чжан Дж. (май 2017 г.). «Классификация Android-приложений и вредоносных программ с использованием глубоких нейронных сетей». Международная совместная конференция по нейронным сетям 2017 (IJCNN) . стр. 1871–1878. doi : 10.1109/IJCNN.2017.7966078 . ISBN 978-1-5090-6182-2 . S2CID 8838479 .
- ^ «Обнаружение вредоносных URL-адресов» . Группа систем и сетей в UCSD . Архивировано из оригинала 14 июля 2019 года . Проверено 15 февраля 2019 г.
- ^ Хомаюн С., Ахмадзаде М., Хашеми С., Дегантанха А., Хаями Р. (2018), Дегантанха А., Конти М., Даргахи Т. (ред.), «BoTShark: подход к глубокому обучению для обнаружения трафика ботнетов», Разведка киберугроз , достижения в области Информационная безопасность, вып. 70, Springer International Publishing, стр. 137–153, номер документа : 10.1007/978-3-319-73951-9_7 , ISBN. 978-3-319-73951-9
- ^ Гош, Рейли (январь 1994 г.). «Обнаружение мошенничества с кредитными картами с помощью нейронной сети». Материалы двадцать седьмой Гавайской международной конференции по системным наукам HICSS-94 . Том. 3. С. 621–630. дои : 10.1109/HICSS.1994.323314 . ISBN 978-0-8186-5090-1 . S2CID 13260377 .
- ^ Анантасвами А (19 апреля 2021 г.). «Новейшие нейронные сети решают сложнейшие в мире уравнения быстрее, чем когда-либо прежде» . Журнал Кванта . Архивировано из оригинала 19 мая 2024 года . Проверено 12 мая 2021 г.
- ^ «ИИ решил ключевую математическую загадку для понимания нашего мира» . Обзор технологий Массачусетского технологического института . Архивировано из оригинала 19 мая 2024 года . Проверено 19 ноября 2020 г. .
- ^ «ИИ с открытым исходным кодом Калифорнийского технологического института для решения уравнений в частных производных» . ИнфоQ . Архивировано из оригинала 25 января 2021 года . Проверено 20 января 2021 г.
- ^ Надь А (28 июня 2019 г.). «Вариационный квантовый метод Монте-Карло с нейросетевым анзацем для открытых квантовых систем». Письма о физических отзывах . 122 (25): 250501. arXiv : 1902.09483 . Бибкод : 2019PhRvL.122y0501N . doi : 10.1103/PhysRevLett.122.250501 . ПМИД 31347886 . S2CID 119074378 .
- ^ Ёсиока Н., Хамазаки Р. (28 июня 2019 г.). «Построение нейронных стационарных состояний для открытых квантовых систем многих тел». Физический обзор B . 99 (21): 214306. arXiv : 1902.07006 . Бибкод : 2019PhRvB..99u4306Y . дои : 10.1103/PhysRevB.99.214306 . S2CID 119470636 .
- ^ Хартманн М.Ю., Карлео Дж. (28 июня 2019 г.). «Нейросетевой подход к диссипативной квантовой динамике многих тел». Письма о физических отзывах . 122 (25): 250502. arXiv : 1902.05131 . Бибкод : 2019PhRvL.122y0502H . doi : 10.1103/PhysRevLett.122.250502 . ПМИД 31347862 . S2CID 119357494 .
- ^ Вичентини Ф, Бьелла А, Реньо Н, Сиути К (28 июня 2019 г.). «Вариационный нейросетевой анзац для устойчивых состояний в открытых квантовых системах». Письма о физических отзывах . 122 (25): 250503. arXiv : 1902.10104 . Бибкод : 2019PhRvL.122y0503V . doi : 10.1103/PhysRevLett.122.250503 . ПМИД 31347877 . S2CID 119504484 .
- ^ Форрест, доктор медицины (апрель 2015 г.). «Моделирование действия алкоголя на подробной модели нейронов Пуркинье и более простой суррогатной модели, которая работает более чем в 400 раз быстрее» . BMC Нейронаука . 16 (27): 27. дои : 10.1186/s12868-015-0162-6 . ПМЦ 4417229 . ПМИД 25928094 .
- ^ Вечорек С., Филипяк Д., Филиповска А. (2018). «Семантическое профилирование интересов пользователей на основе изображений с помощью нейронных сетей» . Исследования семантической сети . 36 (Новые темы семантических технологий). дои : 10.3233/978-1-61499-894-5-179 . Архивировано из оригинала 19 мая 2024 года . Проверено 20 января 2024 г.
- ^ Мерчант А, Бацнер С, Шенхольц СС, Айкол М, Чеон Г, Чубук ЭД (декабрь 2023 г.). «Масштабирование глубокого обучения для открытия материалов» . Природа . 624 (7990): 80–85. Бибкод : 2023Природа.624...80М . дои : 10.1038/s41586-023-06735-9 . ISSN 1476-4687 . ПМЦ 10700131 . ПМИД 38030720 .
- ^ Сигельманн Х, Зонтаг Э (1991). «Вычислимость по Тьюрингу с помощью нейронных сетей» (PDF) . Прил. Математика. Летт . 4 (6): 77–80. дои : 10.1016/0893-9659(91)90080-F . Архивировано (PDF) из оригинала 19 мая 2024 года . Проверено 10 января 2017 г.
- ^ Бэйнс С. (3 ноября 1998 г.). «Аналоговый компьютер превосходит модель Тьюринга» . ЭЭ Таймс . Архивировано из оригинала 11 мая 2023 года . Проверено 11 мая 2023 г.
- ^ Балькасар Дж. (июль 1997 г.). «Вычислительная мощность нейронных сетей: характеристика сложности по Колмогорову». Транзакции IEEE по теории информации . 43 (4): 1175–1183. CiteSeerX 10.1.1.411.7782 . дои : 10.1109/18.605580 .
- ↑ Перейти обратно: Перейти обратно: а б Маккей диджей (2003). Теория информации, вывод и алгоритмы обучения (PDF) . Издательство Кембриджского университета . ISBN 978-0-521-64298-9 . Архивировано (PDF) из оригинала 19 октября 2016 г. Проверено 11 июня 2016 г.
- ^ Обложка Т (1965). «Геометрические и статистические свойства систем линейных неравенств с приложениями в распознавании образов» (PDF) . Транзакции IEEE на электронных компьютерах . ИС-14 (3). ИИЭР : 326–334. дои : 10.1109/PGEC.1965.264137 . Архивировано (PDF) из оригинала 5 марта 2016 года . Проверено 10 марта 2020 г.
- ^ Джеральд Ф (2019). «Воспроизводимость и экспериментальный дизайн машинного обучения аудио и мультимедийных данных». Материалы 27-й Международной конференции ACM по мультимедиа . АКМ . стр. 2709–2710. дои : 10.1145/3343031.3350545 . ISBN 978-1-4503-6889-6 . S2CID 204837170 .
- ^ «Хватит возиться, начни измерять! Предсказуемый экспериментальный дизайн экспериментов с нейронной сетью» . Тензорный расходомер . Архивировано из оригинала 18 апреля 2022 года . Проверено 10 марта 2020 г.
- ^ Ли Дж., Сяо Л., Шенхольц С.С., Бахри Ю., Новак Р., Золь-Дикштейн Дж. и др. (2020). «Широкие нейронные сети любой глубины развиваются как линейные модели при градиентном спуске». Журнал статистической механики: теория и эксперимент . 2020 (12): 124002. arXiv : 1902.06720 . Бибкод : 2020JSMTE2020l4002L . дои : 10.1088/1742-5468/abc62b . S2CID 62841516 .
- ^ Артур Жако, Франк Габриэль, Клемент Хонглер (2018). Нейронное касательное ядро: конвергенция и обобщение в нейронных сетях (PDF) . 32-я конференция по нейронным системам обработки информации (NeurIPS 2018), Монреаль, Канада. Архивировано (PDF) из оригинала 22 июня 2022 года . Проверено 4 июня 2022 г.
- ^ Сюй ZJ, Чжан Ю, Сяо Ю (2019). «Поведение обучения глубокой нейронной сети в частотной области». В Гедеон Т., Вонг К., Ли М. (ред.). Нейронная обработка информации . Конспекты лекций по информатике. Том. 11953. Спрингер, Чам. стр. 264–274. arXiv : 1807.01251 . дои : 10.1007/978-3-030-36708-4_22 . ISBN 978-3-030-36707-7 . S2CID 49562099 .
- ^ Насим Рахаман, Аристид Баратин, Деванш Арпит, Феликс Дракслер, Мин Лин, Фред Хампрехт и др. (2019). «О спектральном смещении нейронных сетей» (PDF) . Материалы 36-й Международной конференции по машинному обучению . 97 : 5301–5310. arXiv : 1806.08734 . Архивировано (PDF) из оригинала 22 октября 2022 года . Проверено 4 июня 2022 г.
- ^ Чжи-Цинь Джон Сюй, Яоюй Чжан, Тао Ло, Яньян Сяо, Чжэн Ма (2020). «Частотный принцип: анализ Фурье проливает свет на глубокие нейронные сети». Коммуникации в вычислительной физике . 28 (5): 1746–1767. arXiv : 1901.06523 . Бибкод : 2020CCoPh..28.1746X . doi : 10.4208/cicp.OA-2020-0085 . S2CID 58981616 .
- ^ Тао Ло, Чжэн Ма, Чжи-Цинь Джон Сюй, Яоюй Чжан (2019). «Теория частотного принципа для глубоких нейронных сетей общего назначения». arXiv : 1906.09235 [ cs.LG ].
- ^ Сюй ZJ, Чжоу Х (18 мая 2021 г.). «Принцип глубокой частоты для понимания того, почему более глубокое обучение происходит быстрее» . Материалы конференции AAAI по искусственному интеллекту . 35 (12): 10541–10550. arXiv : 2007.14313 . дои : 10.1609/aaai.v35i12.17261 . ISSN 2374-3468 . S2CID 220831156 . Архивировано из оригинала 5 октября 2021 года . Проверено 5 октября 2021 г.
- ^ Паризи Дж.И., Кемкер Р., Парт Дж.Л., Кэнан С., Вермтер С. (1 мая 2019 г.). «Непрерывное обучение на протяжении всей жизни с помощью нейронных сетей: обзор» . Нейронные сети . 113 : 54–71. arXiv : 1802.07569 . дои : 10.1016/j.neunet.2019.01.012 . ISSN 0893-6080 . ПМИД 30780045 .
- ^ Дин Померло, «Обучение искусственных нейронных сетей, основанное на знаниях, для автономного вождения роботов»
- ^ Дьюдни АК (1 апреля 1997 г.). Да, у нас нет нейтронов: поучительный экскурс в перипетии плохой науки . Уайли. п. 82. ИСБН 978-0-471-10806-1 .
- ^ НАСА - Центр летных исследований Драйдена - Центр новостей: Выпуски новостей: ПРОЕКТ НЕЙРОННОЙ СЕТИ НАСА ПРОХОДИТ ВЕХУ. Архивировано 2 апреля 2010 г. в Wayback Machine . НАСА.gov. Проверено 20 ноября 2013 г.
- ^ «Защита нейронных сетей Роджером Бриджменом» . Архивировано из оригинала 19 марта 2012 года . Проверено 12 июля 2010 г.
- ^ «Масштабирование алгоритмов обучения для {ИИ} — LISA — Публикации — Aigaion 2.0» . www.iro.umonreal.ca .
- ^ DJ Felleman и DC Van Essen, « Распределенная иерархическая обработка данных в коре головного мозга приматов », Cerebral Cortex , 1, стр. 1–47, 1991.
- ^ Дж. Венг, « Естественный и искусственный интеллект: введение в вычислительный мозг-разум. Архивировано 19 мая 2024 г. в Wayback Machine », BMI Press, ISBN 978-0-9858757-2-5 , 2012.
- ↑ Перейти обратно: Перейти обратно: а б Эдвардс С. (25 июня 2015 г.). «Болезнь роста глубокого обучения». Коммуникации АКМ . 58 (7): 14–16. дои : 10.1145/2771283 . S2CID 11026540 .
- ^ Кейд Мец (18 мая 2016 г.). «Google создала собственные чипы для работы своих ботов с искусственным интеллектом» . Проводной . Архивировано из оригинала 13 января 2018 года . Проверено 5 марта 2017 г.
- ^ «Масштабирование алгоритмов обучения в сторону ИИ» (PDF) . Архивировано (PDF) из оригинала 12 августа 2022 года . Проверено 6 июля 2022 г.
- ^ Тахмасеби, Хезархани (2012). «Гибридные нейронные сети-нечеткая логика-генетический алгоритм оценки оценок» . Компьютеры и геонауки . 42 : 18–27. Бибкод : 2012CG.....42...18T . дои : 10.1016/j.cageo.2012.02.004 . ПМЦ 4268588 . ПМИД 25540468 .
- ↑ Солнце и Книжник, 1990.
- ↑ Перейти обратно: Перейти обратно: а б Норори Н., Ху Кью, Аеллен Ф.М., Фарачи Ф.Д., Цовара А. (октябрь 2021 г.). «Устранение предвзятости в больших данных и искусственном интеллекте в здравоохранении: призыв к открытой науке» . Узоры . 2 (10): 100347. doi : 10.1016/j.patter.2021.100347 . ПМЦ 8515002 . ПМИД 34693373 .
- ↑ Перейти обратно: Перейти обратно: а б Карина В. (27 октября 2022 г.). «Провал по номинальной стоимости: влияние предвзятой технологии распознавания лиц на расовую дискриминацию в уголовном правосудии» . Научные и социальные исследования . 4 (10): 29–40. дои : 10.26689/ssr.v4i10.4402 . ISSN 2661-4332 .
- ↑ Перейти обратно: Перейти обратно: а б Чанг Икс (13 сентября 2023 г.). «Гендерная предвзятость при найме: анализ влияния алгоритма рекрутинга Amazon» . Достижения в области экономики, менеджмента и политических наук . 23 (1): 134–140. дои : 10.54254/2754-1169/23/20230367 . ISSN 2754-1169 . Архивировано из оригинала 9 декабря 2023 года . Проверено 9 декабря 2023 г.
- ^ Кортылевски А., Эггер Б., Шнайдер А., Гериг Т., Морель-Форстер А., Веттер Т. (июнь 2019 г.). «Анализ и уменьшение ущерба от смещения набора данных при распознавании лиц с помощью синтетических данных». Семинары конференции IEEE/CVF 2019 года по компьютерному зрению и распознаванию образов (CVPRW) (PDF) . IEEE. стр. 2261–2268. дои : 10.1109/cvprw.2019.00279 . ISBN 978-1-7281-2506-0 . S2CID 198183828 . Архивировано (PDF) из оригинала 19 мая 2024 года . Проверено 30 декабря 2023 г.
- ↑ Перейти обратно: Перейти обратно: а б с д и ж Хуан Ю (2009). «Достижения в области искусственных нейронных сетей – методологическое развитие и применение» . Алгоритмы . 2 (3): 973–1007. дои : 10.3390/algor2030973 . ISSN 1999-4893 .
- ↑ Перейти обратно: Перейти обратно: а б с д и Карири Э, Луати Х, Луати А, Масмуди Ф (2023). «Изучение достижений и будущих направлений исследований искусственных нейронных сетей: подход к интеллектуальному анализу текста» . Прикладные науки . 13 (5): 3186. дои : 10.3390/app13053186 . ISSN 2076-3417 .
- ↑ Перейти обратно: Перейти обратно: а б Фуй-Хун На Ф, Чжэн Р, Цай Дж, Сиау К, Чен Л (3 июля 2023 г.). «Генераторный ИИ и ChatGPT: приложения, проблемы и сотрудничество ИИ и человека» . Журнал исследований и применений информационных технологий . 25 (3): 277–304. дои : 10.1080/15228053.2023.2233814 . ISSN 1522-8053 .
- ^ «Самое интересное в нем — сбои DALL-E 2 — IEEE Spectrum» . Spectrum.ieee.org . Архивировано из оригинала 15 июля 2022 года . Проверено 9 декабря 2023 г.
- ^ Брио Дж.П. (январь 2021 г.). «От искусственных нейронных сетей к глубокому обучению для генерации музыки: история, концепции и тенденции» . Нейронные вычисления и их приложения . 33 (1): 39–65. дои : 10.1007/s00521-020-05399-0 . ISSN 0941-0643 .
- ^ Чоу PS (6 июля 2020 г.). «Призрак в (Голливудской) машине: новые применения искусственного интеллекта в киноиндустрии». NECSUS_Европейский журнал медиаисследований . дои : 10.25969/MEDIAREP/14307 . ISSN 2213-0217 .
- ^ Ю Х, Хэ С, Гао Ю, Ян Дж, Ша Л, Чжан Ю и др. (июнь 2010 г.). «Динамическая регулировка сложности игрового ИИ для видеоигры Dead-End». 3-я Международная конференция по информатике и наукам о взаимодействии . IEEE. стр. 583–587. дои : 10.1109/icicis.2010.5534761 . ISBN 978-1-4244-7384-7 . S2CID 17555595 .
Библиография [ править ]
- Бхадешиа HKDH (1999). «Нейронные сети в материаловедении» (PDF) . ISIJ International . 39 (10): 966–979. дои : 10.2355/isijinternational.39.966 .
- Епископ К.М. (1995). Нейронные сети для распознавания образов . Кларендон Пресс. ISBN 978-0-19-853849-3 . ОСЛК 33101074 .
- Боргельт С (2003). Нейро-нечеткие системы: от основ искусственных нейронных сетей до связи с нечеткими системами . Посмотретьег. ISBN 978-3-528-25265-6 . OCLC 76538146 .
- Цыбенко Г (2006). «Приближение суперпозициями сигмоидальной функции» . В ван Шуппене Дж. Х. (ред.). Математика управления, сигналов и систем . Спрингер Интернэшнл. стр. 303–314. PDF
- Дьюдни АК (1997). Да, у нас нет нейтронов: поучительный экскурс в перипетии плохой науки . Нью-Йорк: Уайли. ISBN 978-0-471-10806-1 . OCLC 35558945 .
- Дуда Р.О., Харт П.Е., Сторк Д.Г. (2001). Классификация узоров (2-е изд.). Уайли. ISBN 978-0-471-05669-0 . OCLC 41347061 .
- Эгмонт-Петерсен М., де Риддер Д., Гендельс Х. (2002). «Обработка изображений нейронными сетями – обзор». Распознавание образов . 35 (10): 2279–2301. CiteSeerX 10.1.1.21.5444 . дои : 10.1016/S0031-3203(01)00178-9 .
- Фалман С., Лебьер С. (1991). «Архитектура обучения с каскадной корреляцией» (PDF) . Архивировано из оригинала (PDF) 3 мая 2013 года . Проверено 28 августа 2006 г.
- создан для Национального научного фонда , номер контракта EET-8716324, и Агентства перспективных исследовательских проектов Министерства обороны (DOD), приказ ARPA № 4976 в соответствии с контрактом F33615-87-C-1499.
- Герни К. (1997). Введение в нейронные сети . УКЛ Пресс. ISBN 978-1-85728-673-1 . OCLC 37875698 .
- Хайкин С.С. (1999). Нейронные сети: комплексная основа . Прентис Холл. ISBN 978-0-13-273350-2 . OCLC 38908586 .
- Герц Дж., Палмер Р.Г., Крог А.С. (1991). Введение в теорию нейронных вычислений . Аддисон-Уэсли. ISBN 978-0-201-51560-2 . ОСЛК 21522159 .
- Теория информации, логический вывод и алгоритмы обучения . Издательство Кембриджского университета. 25 сентября 2003 г. Бибкод : 2003itil.book.....М . ISBN 978-0-521-64298-9 . OCLC 52377690 .
- Крузе Р., Боргельт С., Клавонн Ф., Мовес С., Штайнбрехер М., Хелд П. (2013). Вычислительный интеллект: методологическое введение . Спрингер. ISBN 978-1-4471-5012-1 . OCLC 837524179 .
- Лоуренс Дж (1994). Введение в нейронные сети: проектирование, теория и приложения . Калифорнийское научное программное обеспечение. ISBN 978-1-883157-00-5 . OCLC 32179420 .
- Мастерс Т (1994). Обработка сигналов и изображений с помощью нейронных сетей: справочник по C++ . Дж. Уайли. ISBN 978-0-471-04963-0 . OCLC 29877717 .
- Маурер Х (2021). Когнитивная наука: механизмы интегративной синхронизации в когнитивных нейроархитектурах современного коннекционизма . ЦРК Пресс. дои : 10.1201/9781351043526 . ISBN 978-1-351-04352-6 . S2CID 242963768 .
- Рипли Б.Д. (2007). Распознавание образов и нейронные сети . Издательство Кембриджского университета. ISBN 978-0-521-71770-0 .
- Сигельманн Х, Зонтаг ЭД (1994). «Аналоговые вычисления с помощью нейронных сетей» . Теоретическая информатика . 131 (2): 331–360. дои : 10.1016/0304-3975(94)90178-3 . S2CID 2456483 .
- Смит М (1993). Нейронные сети для статистического моделирования . Ван Ностранд Рейнхольд. ISBN 978-0-442-01310-3 . OCLC 27145760 .
- Вассерман П.Д. (1993). Передовые методы нейронных вычислений . Ван Ностранд Рейнхольд. ISBN 978-0-442-00461-3 . ОСЛК 27429729 .
- Уилсон Х (2018). Искусственный интеллект . Издательство Грей Хаус. ISBN 978-1-68217-867-6 .

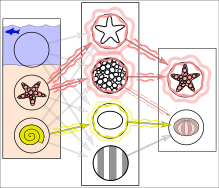



![{\displaystyle \textstyle C=E[(x-f(x))^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2929ecb1606fdfeaddc55477d9671e11c034e21c)