Групповой метод обработки данных

Групповой метод обработки данных (GMDH) — это семейство индуктивных алгоритмов компьютерного математического моделирования многопараметрических наборов данных, которое обеспечивает полностью автоматическую структурную и параметрическую оптимизацию моделей.

GMDH используется в таких областях, как интеллектуальный анализ данных , обнаружение знаний , прогнозирование , сложных систем моделирование , оптимизация и распознавание образов . Алгоритмы GMDH характеризуются индуктивной процедурой, которая осуществляет перебор постепенно усложняющихся полиномиальных моделей и выбор лучшего решения с помощью внешнего критерия .

Модель GMDH с несколькими входами и одним выходом представляет собой подмножество компонентов базовой функции (1):

$Y(x_{1},\dots ,x_{n})=a_{0}+\sum \limits _{i=1}^{m}a_{i}f_{i}$

где f _i — элементарные функции, зависящие от различных наборов входных данных, a _i — коэффициенты, а m — количество компонентов базовой функции.

Чтобы найти лучшее решение, алгоритмы GMDH рассматривают различные подмножества компонентов базовой функции (1), называемые частичными моделями . Коэффициенты этих моделей оцениваются методом наименьших квадратов . Алгоритмы GMDH постепенно увеличивают количество частичных компонентов модели и находят структуру модели с оптимальной сложностью, определяемой минимальным значением внешнего критерия . Этот процесс называется самоорганизацией моделей.

Первой базовой функцией, использованной в GMDH, был постепенно усложняющийся полином Колмогорова – Габора (2):

$Y(x_{1},\dots ,x_{n})=a_{0}+\sum \limits _{i=1}^{n}{a_{i}}x_{i}+\sum \limits _{i=1}^{n}{\sum \limits _{j=i}^{n}{a_{ij}}}x_{i}x_{j}+\sum \limits _{i=1}^{n}{\sum \limits _{j=i}^{n}{\sum \limits _{k=j}^{n}{a_{ijk}}}}x_{i}x_{j}x_{k}+\cdots$

Обычно используются более простые частичные модели с функциями до второй степени.

Индуктивные алгоритмы также известны как полиномиальные нейронные сети . Юрген Шмидхубер называет GMDH одним из первых методов глубокого обучения , отмечая, что он использовался для обучения восьмислойных нейронных сетей еще в 1971 году.

История

Автор ГМДГ – советский учёный профессор А.Г. Ивахненко.

Метод был разработан в 1968 году профессором Алексеем Григорьевичем Ивахненко в Институте кибернетики в Киеве .Этот индуктивный подход с самого начала представлял собой компьютерный метод, поэтому набор компьютерных программ и алгоритмов был основным практическим результатом, достигнутым на основе новых теоретических принципов. Благодаря политике автора по открытому коду метод быстро прижился в большом количестве научных лабораторий по всему миру. Поскольку большая часть рутинной работы переносится на компьютер, влияние человека на объективный результат сведено к минимуму. Фактически, этот подход можно рассматривать как одну из реализаций тезиса об искусственном интеллекте , который утверждает, что компьютер может выступать в качестве мощного советника для человека.

Разработка ГМДГ состоит из синтеза идей из разных областей науки: кибернетической концепции « черного ящика » и принципа последовательного генетический отбор парных признаков , теоремы Гёделя о неполноте и Габора , принцип «свободы выбора решений» и Бера . принцип внешних дополнений

GMDH — оригинальный метод решения задач структурно-параметрической идентификации моделей по экспериментальным данным в условиях неопределенности . Такая проблема возникает при построении математической модели , аппроксимирующей неизвестную закономерность исследуемого объекта или процесса. Он использует информацию о себе, неявно содержащуюся в данных. GMDH отличается от других методов моделирования активным применением следующих принципов : автоматическая генерация моделей, неубедительные решения и последовательный отбор по внешним критериям для поиска моделей оптимальной сложности. В нем использовалась оригинальная многоуровневая процедура автоматического формирования структуры моделей, имитирующая процесс биологического отбора с учетом попарно последовательных признаков. Такая процедура в настоящее время используется в сетях глубокого обучения . Для сравнения и выбора оптимальных моделей используются два или более подмножества выборки данных. Это позволяет избежать предварительных предположений, поскольку разделение выборки неявно учитывает различные типы неопределенностей при автоматическом построении оптимальной модели.

В ходе разработки была установлена ​​органичная аналогия между задачей построения моделей зашумленных данных и прохождением сигнала по каналу с шумом . Это позволило заложить основы теории помехоустойчивого моделирования. Основной результат этой теории состоит в том, что сложность оптимальной прогнозной модели зависит от уровня неопределенности данных: чем выше этот уровень (например, из-за шума), тем проще должна быть оптимальная модель (с меньшим количеством оцениваемых параметров). Это положило начало развитию теории GMDH как индуктивного метода автоматической адаптации оптимальной сложности модели к уровню изменения шума в нечетких данных . Поэтому GMDH часто считают оригинальной информационной технологией извлечения знаний из экспериментальных данных .

Период 1968–1971 гг. характеризуется применением только критерия регулярности для решения задач идентификации, распознавания образов и краткосрочного прогнозирования. В качестве эталонных функций использовались полиномы, логические сети, нечеткие множества Заде и формулы вероятности Байеса. Авторов порадовала очень высокая точность прогнозирования при использовании нового подхода. Помехоустойчивость не исследовалась.

Период 1972–1975 гг . Решена проблема моделирования зашумленных данных и неполной информационной базы. Предложен многокритериальный отбор и использование дополнительной априорной информации для повышения помехоустойчивости. Лучшие эксперименты показали, что при расширенном определении оптимальной модели по дополнительному критерию уровень шума может быть в десять раз больше сигнала. Затем она была улучшена с использованием Теоремы Шеннона об общей теории коммуникации.

Период 1976–1979 гг . Исследована сходимость многоуровневых алгоритмов GMDH. Показано, что некоторые многослойные алгоритмы имеют «ошибку многослойности» – аналогичную статической ошибке систем управления. В 1977 г. было предложено решение задач анализа объективных систем с помощью многоуровневых алгоритмов GMDH. Оказалось, что сортировка по ансамблю критериев позволяет найти единственную оптимальную систему уравнений и, следовательно, выявить элементы сложного объекта, их основные входные и выходные переменные.

Период 1980–1988 гг . Получено много важных теоретических результатов. Стало ясно, что полные физические модели нельзя использовать для долгосрочного прогнозирования. Доказано, что нефизические модели ГМДГ более точны для аппроксимации и прогнозирования, чем физические модели регрессионного анализа. Были разработаны двухуровневые алгоритмы, использующие для моделирования два разных временных масштаба.

С 1989 г. были разработаны и исследованы новые алгоритмы (AC, OCC, PF) непараметрического моделирования нечетких объектов и SLP для экспертных систем. Современный этап развития GMDH можно охарактеризовать как расцвет нейросетей глубокого обучения и параллельных индуктивных алгоритмов для многопроцессорных компьютеров.

Внешние критерии

Внешний критерий является одной из ключевых особенностей ГМДГ. Критерий описывает требования к модели, например минимизацию метода наименьших квадратов . Он всегда рассчитывается с использованием отдельной части выборки данных, которая не использовалась для оценки коэффициентов. Это дает возможность выбрать модель оптимальной сложности по уровню неопределенности входных данных. Существует несколько популярных критериев:

• Критерий регулярности (CR) – наименьшие квадраты модели по выборке B.
• Критерий минимальной систематической ошибки или согласованности - квадратичная ошибка разницы между оцененными выходными данными (или векторами коэффициентов) двух моделей, разработанных на основе двух различных выборок A и B, деленная на квадрат выходных данных, оцененных по выборке B. Сравнение моделей, использующих его. , позволяет получить согласованные модели и восстановить скрытый физический закон из зашумленных данных.
• Критерии перекрестной проверки .

Простое описание разработки модели с использованием GMDH

Для моделирования с использованием GMDH предварительно выбираются только критерий выбора и максимальная сложность модели. Затем процесс проектирования начинается с первого слоя и продолжается. Количество слоев и нейронов в скрытых слоях, структура модели определяются автоматически. Могут быть рассмотрены все возможные комбинации допустимых входов (все возможные нейроны). Затем полиномиальные коэффициенты определяются с использованием одного из доступных методов минимизации, такого как разложение по сингулярным значениям (с обучающими данными). Затем нейроны, имеющие лучшее значение внешнего критерия (для данных тестирования), сохраняются, а другие удаляются. Если внешний критерий лучшего нейрона слоя достигает минимума или превосходит критерий остановки, проектирование сети завершается и полиномиальное выражение лучшего нейрона последнего слоя вводится как функция математического прогнозирования; если нет, то будет создан следующий слой, и этот процесс продолжится.

Нейронные сети типа GMDH

Выбрать заказ на рассмотрение частичных моделей можно разными способами. Самый первый порядок рассмотрения, используемый в GMDH и первоначально названный многослойной индуктивной процедурой, является наиболее популярным. Это перебор постепенно усложняющихся моделей, генерируемых из базовой функции . На лучшую модель указывает минимум внешней критериальной характеристики. Многоуровневая процедура эквивалентна искусственной нейронной сети с полиномиальной функцией активации нейронов. Поэтому алгоритм с таким подходом обычно называют нейронной сетью типа GMDH или полиномиальной нейронной сетью. Ли показал, что нейронная сеть типа GMDH работает лучше, чем классические алгоритмы прогнозирования, такие как Single Exponential Smooth, Double Exponential Smooth, ARIMA и нейронная сеть обратного распространения ошибки.

Комбинаторная ГМДГ

Рис.1. Типичное распределение минимальных значений критерия регулярности для комбинаторных моделей GMDH различной сложности.

Еще одним важным подходом к рассмотрению частичных моделей, который становится все более популярным, является комбинаторный поиск, который может быть либо ограниченным, либо полным. Этот подход имеет некоторые преимущества по сравнению с полиномиальными нейронными сетями, но требует значительной вычислительной мощности и, следовательно, неэффективен для объектов с большим количеством входных данных. Важным достижением комбинаторного GMDH является то, что он полностью превосходит подход линейной регрессии, если уровень шума во входных данных больше нуля. Это гарантирует, что в ходе исчерпывающей сортировки будет найдена наиболее оптимальная модель.

Базовый комбинаторный алгоритм выполняет следующие шаги:

• Делит выборку данных как минимум на две выборки A и B.
• Генерирует подвыборки из A в соответствии с частичными моделями с постоянно возрастающей сложностью.
• Оценивает коэффициенты частичных моделей на каждом уровне сложности модели.
• Рассчитывает значение внешнего критерия для моделей на выборке B.
• Выбирает лучшую модель (набор моделей), указанную по минимальному значению критерия.
• Для выбранной модели оптимальной сложности пересчитываем коэффициенты на всей выборке данных.

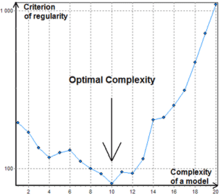
В отличие от нейронных сетей типа GMDH комбинаторный алгоритм обычно не останавливается на определенном уровне сложности, поскольку точкой увеличения значения критерия может быть просто локальный минимум, см. рис.1.

Алгоритмы

• Комбинаторный (КОМБИ)
• Многоуровневая итерация (MIA)
• ГН
• Объективный системный анализ (OSA)
• Гармоничный
• Двухуровневый (АРИМАД)
• Мультипликативно-аддитивный (МАА)
• Объективная компьютерная кластеризация (OCC);
• Алгоритм кластеризации Pointing Finger (PF);
• Комплексообразование аналогов (АК)
• Гармоническая редискретизация
• Алгоритм на основе многослойной теории статистических решений (MTSD)
• Группа эволюции адаптивных моделей (ИГРА)

Список программного обеспечения

• Проект FAKE GAME — с открытым исходным кодом. Кроссплатформенность.
• ГЭвом — Бесплатно по запросу для академического использования. Только для Windows.
• GMDH Shell — программное обеспечение для прогнозной аналитики и прогнозирования временных рядов на основе GMDH. Доступны бесплатная академическая лицензия и бесплатная пробная версия. Только для Windows.
• KnowledgeMiner — Коммерческий продукт. Только для Mac OS X. Доступна бесплатная демо-версия.
• Клиент PNN Discovery — Коммерческий продукт.
• Научный РПФ! — Бесплатное ПО, с открытым исходным кодом.
• wGMDH — плагин Weka , с открытым исходным кодом.
• Пакет R – открытый исходный код.
• Пакет R для задач регрессии – с открытым исходным кодом.
• Библиотека Python алгоритма MIA — с открытым исходным кодом.
• Библиотека Python основных алгоритмов GMDH (COMBI, MULTI, MIA, RIA) — с открытым исходным кодом.

Внешние ссылки

• Библиотека книг и статей GMDH
• Групповой метод обработки данных

Дальнейшее чтение

• АГ Ивахненко. Эвристическая самоорганизация в задачах технической кибернетики , Автоматика, т.6, 1970 — с. 207-219.
• С. Дж. Фарлоу . Методы самоорганизации в моделировании: алгоритмы типа GMDH . Нью-Йорк, Базель: Marcel Decker Inc., 1984, 350 стр.
• Х. Р. Мадала, А. Г. Ивахненко. Алгоритмы индуктивного обучения для моделирования сложных систем . CRC Press, Бока-Ратон, 1994.