Сверточная нейронная сеть

Чтобы узнать о других значениях, см. CNN (значения) .

Сверточная нейронная сеть ( CNN ) — это регуляризованный тип нейронной сети с прямой связью изучает разработку функций , которая самостоятельно посредством оптимизации фильтров (или ядра). Исчезающие и взрывные градиенты, наблюдаемые во время обратного распространения ошибки в более ранних нейронных сетях, предотвращаются за счет использования регуляризованных весов для меньшего количества соединений. Например, для каждого нейрона полносвязного слоя потребуется 10 000 весов для обработки изображения размером 100 × 100 пикселей. Однако, применяя ядра каскадной свертки (или взаимной корреляции), для обработки плиток размером 5x5 требуется всего 25 нейронов. Функции более высокого уровня извлекаются из более широких контекстных окон по сравнению с функциями более низкого уровня.

У них есть приложения:

• распознавание изображений и видео ,
• рекомендательные системы ,
• классификация изображений ,
• сегментация изображений ,
• анализ медицинских изображений ,
• обработка естественного языка ,
• интерфейсы мозг-компьютер , и
• financial time series.

CNNs are also known as shift invariant or space invariant artificial neural networks (SIANN), based on the shared-weight architecture of the convolution kernels or filters that slide along input features and provide translation-equivariant responses known as feature maps. Counter-intuitively, most convolutional neural networks are not invariant to translation, due to the downsampling operation they apply to the input.

Feed-forward neural networks are usually fully connected networks, that is, each neuron in one layer is connected to all neurons in the next layer. The "full connectivity" of these networks makes them prone to overfitting data. Typical ways of regularization, or preventing overfitting, include: penalizing parameters during training (such as weight decay) or trimming connectivity (skipped connections, dropout, etc.) Robust datasets also increase the probability that CNNs will learn the generalized principles that characterize a given dataset rather than the biases of a poorly-populated set.

Convolutional networks were inspired by biological processes in that the connectivity pattern between neurons resembles the organization of the animal visual cortex. Individual cortical neurons respond to stimuli only in a restricted region of the visual field known as the receptive field. The receptive fields of different neurons partially overlap such that they cover the entire visual field.

CNNs use relatively little pre-processing compared to other image classification algorithms. This means that the network learns to optimize the filters (or kernels) through automated learning, whereas in traditional algorithms these filters are hand-engineered. This independence from prior knowledge and human intervention in feature extraction is a major advantage.

Architecture

Comparison of the LeNet and AlexNet convolution, pooling and dense layers
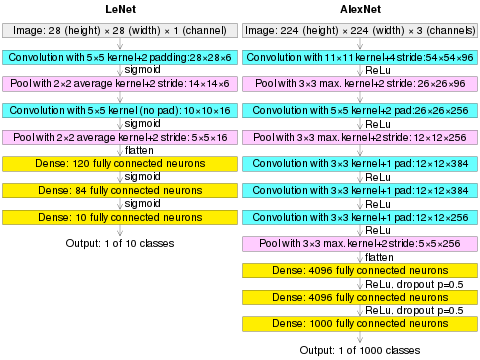
(AlexNet image size should be 227×227×3, instead of 224×224×3, so the math will come out right. The original paper said different numbers, but Andrej Karpathy, the head of computer vision at Tesla, said it should be 227×227×3 (he said Alex didn't describe why he put 224×224×3). The next convolution should be 11×11 with stride 4: 55×55×96 (instead of 54×54×96). It would be calculated, for example, as: [(input width 227 - kernel width 11) / stride 4] + 1 = [(227 - 11) / 4] + 1 = 55. Since the kernel output is the same length as width, its area is 55×55.)

Main article: Layer (deep learning)

A convolutional neural network consists of an input layer, hidden layers and an output layer. In a convolutional neural network, the hidden layers include one or more layers that perform convolutions. Typically this includes a layer that performs a dot product of the convolution kernel with the layer's input matrix. This product is usually the Frobenius inner product, and its activation function is commonly ReLU. As the convolution kernel slides along the input matrix for the layer, the convolution operation generates a feature map, which in turn contributes to the input of the next layer. This is followed by other layers such as pooling layers, fully connected layers, and normalization layers.Here it should be noted how close a convolutional neural network is to a matched filter.

Convolutional layers

In a CNN, the input is a tensor with shape:

(number of inputs) × (input height) × (input width) × (input channels)

After passing through a convolutional layer, the image becomes abstracted to a feature map, also called an activation map, with shape:

(number of inputs) × (feature map height) × (feature map width) × (feature map channels).

Convolutional layers convolve the input and pass its result to the next layer. This is similar to the response of a neuron in the visual cortex to a specific stimulus. Each convolutional neuron processes data only for its receptive field.

1D convolutional neural network feed forward example

Although fully connected feedforward neural networks can be used to learn features and classify data, this architecture is generally impractical for larger inputs (e.g., high-resolution images), which would require massive numbers of neurons because each pixel is a relevant input feature. A fully connected layer for an image of size 100 × 100 has 10,000 weights for each neuron in the second layer. Convolution reduces the number of free parameters, allowing the network to be deeper. For example, using a 5 × 5 tiling region, each with the same shared weights, requires only 25 neurons. Using regularized weights over fewer parameters avoids the vanishing gradients and exploding gradients problems seen during backpropagation in earlier neural networks.

To speed processing, standard convolutional layers can be replaced by depthwise separable convolutional layers, which are based on a depthwise convolution followed by a pointwise convolution. The depthwise convolution is a spatial convolution applied independently over each channel of the input tensor, while the pointwise convolution is a standard convolution restricted to the use of $1\times 1$ kernels.

Pooling layers

Convolutional networks may include local and/or global pooling layers along with traditional convolutional layers. Pooling layers reduce the dimensions of data by combining the outputs of neuron clusters at one layer into a single neuron in the next layer. Local pooling combines small clusters, tiling sizes such as 2 × 2 are commonly used. Global pooling acts on all the neurons of the feature map. There are two common types of pooling in popular use: max and average. Max pooling uses the maximum value of each local cluster of neurons in the feature map, while average pooling takes the average value.

Fully connected layers

Fully connected layers connect every neuron in one layer to every neuron in another layer. It is the same as a traditional multilayer perceptron neural network (MLP). The flattened matrix goes through a fully connected layer to classify the images.

Receptive field

In neural networks, each neuron receives input from some number of locations in the previous layer. In a convolutional layer, each neuron receives input from only a restricted area of the previous layer called the neuron's receptive field. Typically the area is a square (e.g. 5 by 5 neurons). Whereas, in a fully connected layer, the receptive field is the entire previous layer. Thus, in each convolutional layer, each neuron takes input from a larger area in the input than previous layers. This is due to applying the convolution over and over, which takes the value of a pixel into account, as well as its surrounding pixels. When using dilated layers, the number of pixels in the receptive field remains constant, but the field is more sparsely populated as its dimensions grow when combining the effect of several layers.

To manipulate the receptive field size as desired, there are some alternatives to the standard convolutional layer. For example, atrous or dilated convolution expands the receptive field size without increasing the number of parameters by interleaving visible and blind regions. Moreover, a single dilated convolutional layer can comprise filters with multiple dilation ratios, thus having a variable receptive field size.

Weights

Each neuron in a neural network computes an output value by applying a specific function to the input values received from the receptive field in the previous layer. The function that is applied to the input values is determined by a vector of weights and a bias (typically real numbers). Learning consists of iteratively adjusting these biases and weights.

The vectors of weights and biases are called filters and represent particular features of the input (e.g., a particular shape). A distinguishing feature of CNNs is that many neurons can share the same filter. This reduces the memory footprint because a single bias and a single vector of weights are used across all receptive fields that share that filter, as opposed to each receptive field having its own bias and vector weighting.

History

CNN are often compared to the way the brain achieves vision processing in living organisms.

Receptive fields in the visual cortex

Work by Hubel and Wiesel in the 1950s and 1960s showed that cat visual cortices contain neurons that individually respond to small regions of the visual field. Provided the eyes are not moving, the region of visual space within which visual stimuli affect the firing of a single neuron is known as its receptive field. Neighboring cells have similar and overlapping receptive fields. Receptive field size and location varies systematically across the cortex to form a complete map of visual space. The cortex in each hemisphere represents the contralateral visual field.

Their 1968 paper identified two basic visual cell types in the brain:

• simple cells, whose output is maximized by straight edges having particular orientations within their receptive field
• complex cells, which have larger receptive fields, whose output is insensitive to the exact position of the edges in the field.

Hubel and Wiesel also proposed a cascading model of these two types of cells for use in pattern recognition tasks.

Neocognitron, origin of the CNN architecture

The "neocognitron" was introduced by Kunihiko Fukushima in 1980.It was inspired by the above-mentioned work of Hubel and Wiesel. The neocognitron introduced the two basic types of layers in CNNs:

• A convolutional layer which contains units whose receptive fields cover a patch of the previous layer. The weight vector (the set of adaptive parameters) of such a unit is often called a filter. Units can share filters.
• Downsampling layers which contain units whose receptive fields cover patches of previous convolutional layers. Such a unit typically computes the average of the activations of the units in its patch. This downsampling helps to correctly classify objects in visual scenes even when the objects are shifted.

In 1969, Kunihiko Fukushima also introduced the ReLU (rectified linear unit) activation function. The rectifier has become the most popular activation function for CNNs and deep neural networks in general.

In a variant of the neocognitron called the cresceptron, instead of using Fukushima's spatial averaging, J. Weng et al. in 1993 introduced a method called max-pooling where a downsampling unit computes the maximum of the activations of the units in its patch. Max-pooling is often used in modern CNNs.

Several supervised and unsupervised learning algorithms have been proposed over the decades to train the weights of a neocognitron. Today, however, the CNN architecture is usually trained through backpropagation.

The neocognitron is the first CNN which requires units located at multiple network positions to have shared weights.

Convolutional neural networks were presented at the Neural Information Processing Workshop in 1987, automatically analyzing time-varying signals by replacing learned multiplication with convolution in time, and demonstrated for speech recognition.

Time delay neural networks

The time delay neural network (TDNN) was introduced in 1987 by Alex Waibel et al. for phoneme recognition and was one of the first convolutional networks, as it achieved shift-invariance. A TDNN is a 1-D convolutional neural net where the convolution is performed along the time axis of the data. It is the first CNN utilizing weight sharing in combination with a training by gradient descent, using backpropagation. Thus, while also using a pyramidal structure as in the neocognitron, it performed a global optimization of the weights instead of a local one.

TDNNs are convolutional networks that share weights along the temporal dimension. They allow speech signals to be processed time-invariantly. In 1990 Hampshire and Waibel introduced a variant that performs a two-dimensional convolution. Since these TDNNs operated on spectrograms, the resulting phoneme recognition system was invariant to both time and frequency shifts. This inspired translation invariance in image processing with CNNs. The tiling of neuron outputs can cover timed stages.

TDNNs now achieve the best performance in far-distance speech recognition.

Max pooling

In 1990 Yamaguchi et al. introduced the concept of max pooling, a fixed filtering operation that calculates and propagates the maximum value of a given region. They did so by combining TDNNs with max pooling to realize a speaker-independent isolated word recognition system. In their system they used several TDNNs per word, one for each syllable. The results of each TDNN over the input signal were combined using max pooling and the outputs of the pooling layers were then passed on to networks performing the actual word classification.

Image recognition with CNNs trained by gradient descent

Denker et al. (1989) designed a 2-D CNN system to recognize hand-written ZIP Code numbers. However, the lack of an efficient training method to determine the kernel coefficients of the involved convolutions meant that all the coefficients had to be laboriously hand-designed.

Following the advances in the training of 1-D CNNs by Waibel et al. (1987), Yann LeCun et al. (1989) used back-propagation to learn the convolution kernel coefficients directly from images of hand-written numbers. Learning was thus fully automatic, performed better than manual coefficient design, and was suited to a broader range of image recognition problems and image types. Wei Zhang et al. (1988) used back-propagation to train the convolution kernels of a CNN for alphabets recognition. The model was called Shift-Invariant Artificial Neural Network (SIANN) before the name CNN was coined later in the early 1990s. Wei Zhang et al. also applied the same CNN without the last fully connected layer for medical image object segmentation (1991) and breast cancer detection in mammograms (1994).

This approach became a foundation of modern computer vision.

LeNet-5

Main article: LeNet

LeNet-5, a pioneering 7-level convolutional network by LeCun et al. in 1995, classifies hand-written numbers on checks (British English: cheques) digitized in 32x32 pixel images. The ability to process higher-resolution images requires larger and more layers of convolutional neural networks, so this technique is constrained by the availability of computing resources.

It was superior than other commercial courtesy amount reading systems (as of 1995). The system was integrated in NCR's check reading systems, and fielded in several American banks since June 1996, reading millions of checks per day.

Shift-invariant neural network

A shift-invariant neural network was proposed by Wei Zhang et al. for image character recognition in 1988. It is a modified Neocognitron by keeping only the convolutional interconnections between the image feature layers and the last fully connected layer. The model was trained with back-propagation. The training algorithm was further improved in 1991 to improve its generalization ability. The model architecture was modified by removing the last fully connected layer and applied for medical image segmentation (1991) and automatic detection of breast cancer in mammograms (1994).

A different convolution-based design was proposed in 1988 for application to decomposition of one-dimensional electromyography convolved signals via de-convolution. This design was modified in 1989 to other de-convolution-based designs.

Neural abstraction pyramid

Neural abstraction pyramid

The feed-forward architecture of convolutional neural networks was extended in the neural abstraction pyramid by lateral and feedback connections. The resulting recurrent convolutional network allows for the flexible incorporation of contextual information to iteratively resolve local ambiguities. In contrast to previous models, image-like outputs at the highest resolution were generated, e.g., for semantic segmentation, image reconstruction, and object localization tasks.

GPU implementations

Although CNNs were invented in the 1980s, their breakthrough in the 2000s required fast implementations on graphics processing units (GPUs).

In 2004, it was shown by K. S. Oh and K. Jung that standard neural networks can be greatly accelerated on GPUs. Their implementation was 20 times faster than an equivalent implementation on CPU. In 2005, another paper also emphasised the value of GPGPU for machine learning.

The first GPU-implementation of a CNN was described in 2006 by K. Chellapilla et al. Their implementation was 4 times faster than an equivalent implementation on CPU. Subsequent work also used GPUs, initially for other types of neural networks (different from CNNs), especially unsupervised neural networks.

In 2010, Dan Ciresan et al. at IDSIA showed that even deep standard neural networks with many layers can be quickly trained on GPU by supervised learning through the old method known as backpropagation. Their network outperformed previous machine learning methods on the MNIST handwritten digits benchmark. In 2011, they extended this GPU approach to CNNs, achieving an acceleration factor of 60, with impressive results. In 2011, they used such CNNs on GPU to win an image recognition contest where they achieved superhuman performance for the first time. Between May 15, 2011, and September 30, 2012, their CNNs won no less than four image competitions. In 2012, they also significantly improved on the best performance in the literature for multiple image databases, including the MNIST database, the NORB database, the HWDB1.0 dataset (Chinese characters) and the CIFAR10 dataset (dataset of 60000 32x32 labeled RGB images).

Subsequently, a similar GPU-based CNN by Alex Krizhevsky et al. won the ImageNet Large Scale Visual Recognition Challenge 2012. A very deep CNN with over 100 layers by Microsoft won the ImageNet 2015 contest.

Intel Xeon Phi implementations

Compared to the training of CNNs using GPUs, not much attention was given to the Intel Xeon Phi coprocessor.A notable development is a parallelization method for training convolutional neural networks on the Intel Xeon Phi, named Controlled Hogwild with Arbitrary Order of Synchronization (CHAOS).CHAOS exploits both the thread- and SIMD-level parallelism that is available on the Intel Xeon Phi.

Distinguishing features

In the past, traditional multilayer perceptron (MLP) models were used for image recognition. However, the full connectivity between nodes caused the curse of dimensionality, and was computationally intractable with higher-resolution images. A 1000×1000-pixel image with RGB color channels has 3 million weights per fully-connected neuron, which is too high to feasibly process efficiently at scale.

CNN layers arranged in 3 dimensions

For example, in CIFAR-10, images are only of size 32×32×3 (32 wide, 32 high, 3 color channels), so a single fully connected neuron in the first hidden layer of a regular neural network would have 32*32*3 = 3,072 weights. A 200×200 image, however, would lead to neurons that have 200*200*3 = 120,000 weights.

Also, such network architecture does not take into account the spatial structure of data, treating input pixels which are far apart in the same way as pixels that are close together. This ignores locality of reference in data with a grid-topology (such as images), both computationally and semantically. Thus, full connectivity of neurons is wasteful for purposes such as image recognition that are dominated by spatially local input patterns.

Convolutional neural networks are variants of multilayer perceptrons, designed to emulate the behavior of a visual cortex. These models mitigate the challenges posed by the MLP architecture by exploiting the strong spatially local correlation present in natural images. As opposed to MLPs, CNNs have the following distinguishing features:

• 3D volumes of neurons. The layers of a CNN have neurons arranged in 3 dimensions: width, height and depth. Where each neuron inside a convolutional layer is connected to only a small region of the layer before it, called a receptive field. Distinct types of layers, both locally and completely connected, are stacked to form a CNN architecture.
• Local connectivity: following the concept of receptive fields, CNNs exploit spatial locality by enforcing a local connectivity pattern between neurons of adjacent layers. The architecture thus ensures that the learned "filters" produce the strongest response to a spatially local input pattern. Stacking many such layers leads to nonlinear filters that become increasingly global (i.e. responsive to a larger region of pixel space) so that the network first creates representations of small parts of the input, then from them assembles representations of larger areas.
• Shared weights: In CNNs, each filter is replicated across the entire visual field. These replicated units share the same parameterization (weight vector and bias) and form a feature map. This means that all the neurons in a given convolutional layer respond to the same feature within their specific response field. Replicating units in this way allows for the resulting activation map to be equivariant under shifts of the locations of input features in the visual field, i.e. they grant translational equivariance - given that the layer has a stride of one.
• Pooling: In a CNN's pooling layers, feature maps are divided into rectangular sub-regions, and the features in each rectangle are independently down-sampled to a single value, commonly by taking their average or maximum value. In addition to reducing the sizes of feature maps, the pooling operation grants a degree of local translational invariance to the features contained therein, allowing the CNN to be more robust to variations in their positions.

Together, these properties allow CNNs to achieve better generalization on vision problems. Weight sharing dramatically reduces the number of free parameters learned, thus lowering the memory requirements for running the network and allowing the training of larger, more powerful networks.

Building blocks

A CNN architecture is formed by a stack of distinct layers that transform the input volume into an output volume (e.g. holding the class scores) through a differentiable function. A few distinct types of layers are commonly used. These are further discussed below.

Neurons of a convolutional layer (blue), connected to their receptive field (red)

Convolutional layer

The convolutional layer is the core building block of a CNN. The layer's parameters consist of a set of learnable filters (or kernels), which have a small receptive field, but extend through the full depth of the input volume. During the forward pass, each filter is convolved across the width and height of the input volume, computing the dot product between the filter entries and the input, producing a 2-dimensional activation map of that filter. As a result, the network learns filters that activate when it detects some specific type of feature at some spatial position in the input.

Stacking the activation maps for all filters along the depth dimension forms the full output volume of the convolution layer. Every entry in the output volume can thus also be interpreted as an output of a neuron that looks at a small region in the input. Each entry in an activation map use the same set of parameters that define the filter.

Self-supervised learning has been adapted for use in convolutional layers by using sparse patches with a high-mask ratio and a global response normalization layer.

Local connectivity

Typical CNN architecture

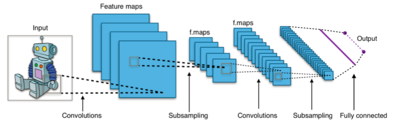
When dealing with high-dimensional inputs such as images, it is impractical to connect neurons to all neurons in the previous volume because such a network architecture does not take the spatial structure of the data into account. Convolutional networks exploit spatially local correlation by enforcing a sparse local connectivity pattern between neurons of adjacent layers: each neuron is connected to only a small region of the input volume.

The extent of this connectivity is a hyperparameter called the receptive field of the neuron. The connections are local in space (along width and height), but always extend along the entire depth of the input volume. Such an architecture ensures that the learned (British English: learnt) filters produce the strongest response to a spatially local input pattern.

Spatial arrangement

Three hyperparameters control the size of the output volume of the convolutional layer: the depth, stride, and padding size:

• The depth of the output volume controls the number of neurons in a layer that connect to the same region of the input volume. These neurons learn to activate for different features in the input. For example, if the first convolutional layer takes the raw image as input, then different neurons along the depth dimension may activate in the presence of various oriented edges, or blobs of color.
• Stride controls how depth columns around the width and height are allocated. If the stride is 1, then we move the filters one pixel at a time. This leads to heavily overlapping receptive fields between the columns, and to large output volumes. For any integer ${\textstyle S>0,}$ a stride S means that the filter is translated S units at a time per output. In practice, ${\textstyle S\geq 3}$ is rare. A greater stride means smaller overlap of receptive fields and smaller spatial dimensions of the output volume.
• Sometimes, it is convenient to pad the input with zeros (or other values, such as the average of the region) on the border of the input volume. The size of this padding is a third hyperparameter. Padding provides control of the output volume's spatial size. In particular, sometimes it is desirable to exactly preserve the spatial size of the input volume, this is commonly referred to as "same" padding.

Пространственный размер выходного тома является функцией размера входного тома. $W$, the kernel field size $K$ of the convolutional layer neurons, the stride $S$и количество заполнения нулями $P$ на границе. Тогда количество нейронов, «помещающихся» в данном объеме, равно:

$${\frac {W-K+2P}{S}}+1.$$

Если это число не является целым числом , то шаги неверны, и нейроны не могут быть выложены плиткой, чтобы симметрично разместиться во входном объеме . В общем, установка нулевого заполнения будет ${\textstyle P=(K-1)/2}$ когда шаг $S=1$ гарантирует, что входной и выходной том будут иметь одинаковый пространственный размер. Однако не всегда полностью необходимо задействовать все нейроны предыдущего слоя. Например, разработчик нейронной сети может решить использовать только часть заполнения.

Совместное использование параметров

Схема совместного использования параметров используется в сверточных слоях для управления количеством свободных параметров. Он основан на предположении, что если объект-заплатку полезно вычислить в какой-то пространственной позиции, то его также полезно вычислить и в других позициях. Обозначая одиночный двумерный срез глубины как срез глубины , нейроны в каждом срезе глубины ограничены использованием одних и тех же весов и смещений.

Поскольку все нейроны в одном срезе глубины имеют одни и те же параметры, прямой проход в каждом срезе глубины сверточного слоя можно вычислить как свертку весов нейронов с входным объемом. Поэтому наборы весов принято называть фильтром (или ядром ) , который свернут с входными данными. Результатом этой свертки является карта активации , а набор карт активации для каждого отдельного фильтра складываются вместе по измерению глубины для получения выходного объема. Совместное использование параметров способствует трансляционной инвариантности архитектуры CNN.

Иногда предположение о совместном использовании параметров может не иметь смысла. Это особенно актуально, когда входные изображения в CNN имеют определенную центрированную структуру; для которого мы ожидаем, что в разных пространственных точках будут изучены совершенно разные функции. Одним из практических примеров является случай, когда входными данными являются лица, которые были центрированы на изображении: мы могли бы ожидать, что в разных частях изображения будут изучены разные особенности глаз или волос. В этом случае принято ослаблять схему совместного использования параметров и вместо этого просто называть уровень «локально подключенным уровнем».

Слой объединения

Максимальное объединение с фильтром 2x2 и шагом = 2

Другая важная концепция CNN — это объединение, которое представляет собой форму нелинейной понижающей дискретизации . Существует несколько нелинейных функций для реализации пула, максимальный пул наиболее распространенной из которых является . Он разбивает входное изображение на набор прямоугольников и для каждой такой подобласти выводит максимум.

Интуитивно понятно, что точное местоположение объекта менее важно, чем его приблизительное расположение относительно других объектов. В этом заключается идея использования пула в сверточных нейронных сетях. Уровень объединения служит для постепенного уменьшения пространственного размера представления, уменьшения количества параметров, объема памяти и объема вычислений в сети и, следовательно, для контроля переобучения . Это известно как понижающая выборка. Обычно периодически вставляют слой объединения между последовательными сверточными уровнями (за каждым из которых обычно следует функция активации, такая как уровень ReLU ). в архитектуре CNN Хотя уровни объединения способствуют локальной трансляционной инвариантности, они не обеспечивают глобальную трансляционную инвариантность в CNN, если не используется форма глобального пула. Слой объединения обычно работает независимо на каждой глубине или срезе входных данных и изменяет их пространственный размер. Очень распространенной формой максимального пула является слой с фильтрами размера 2×2, применяемыми с шагом 2, который субдискретизирует каждый срез глубины во входных данных на 2 как по ширине, так и по высоте, отбрасывая 75% активаций:

$$f_{X,Y}(S)=\max _{a,b=0}^{1}S_{2X+a,2Y+b}.$$

В этом случае каждая максимальная операция превышает 4 числа. Размер глубины остается неизменным (это справедливо и для других форм объединения).

В дополнение к максимальному объединению, объединяющие единицы могут использовать другие функции, такие как среднее объединение или ℓ ₂ -нормы объединение . Исторически часто использовалось среднее объединение, но в последнее время оно вышло из моды по сравнению с максимальным объединением, которое на практике обычно работает лучше.

Из-за эффектов быстрого пространственного уменьшения размера представления, в последнее время наблюдается тенденция к использованию фильтров меньшего размера. или вообще отказаться от слоев объединения.

Объединение ROI до размера 2x2. В этом примере предложение региона (входной параметр) имеет размер 7x5.

Объединение « области интереса » (также известное как объединение областей интереса) — это вариант максимального объединения, при котором выходной размер фиксирован, а входной прямоугольник является параметром.

Пул — это метод понижающей дискретизации и важный компонент сверточных нейронных сетей для обнаружения объектов на основе Fast R-CNN. архитектура.

Максимальное объединение каналов

Уровень операции максимального объединения каналов (CMP) выполняет операцию MP вдоль стороны канала среди соответствующих позиций последовательных карт признаков с целью устранения избыточной информации. CMP позволяет собрать важные функции в меньшем количестве каналов, что важно для более детальной классификации изображений, требующей большего количества различающих функций. Между тем, еще одним преимуществом операции CMP является уменьшение количества каналов карт объектов перед их подключением к первому полносвязному (FC) уровню. Подобно операции MP, мы обозначаем входные карты признаков и выходные карты признаков слоя CMP как F ∈ R(C×M×N) и C ∈ R(c×M×N) соответственно, где C и c — это номера каналов входных и выходных карт объектов, M и N — это ширина и высота карт объектов соответственно. Обратите внимание, что операция CMP изменяет только номер канала карт объектов. Ширина и высота карт объектов не изменяются, в отличие от операции MP.

Слой ReLU

ReLU — это аббревиатура выпрямленной линейной единицы, введенная Кунихико Фукусимой в 1969 году. без насыщения ReLU применяет функцию активации ${\textstyle f(x)=\max(0,x)}$. Он эффективно удаляет отрицательные значения из карты активации, устанавливая их равными нулю. Это вносит нелинейность в функцию принятия решения и в сеть в целом, не затрагивая рецептивные поля слоев свертки.В 2011 году Ксавье Глоро, Антуан Бордес и Йошуа Бенжио обнаружили, что ReLU позволяет лучше обучать более глубокие сети. по сравнению с широко используемыми функциями активации до 2011 года.

Для увеличения нелинейности также можно использовать другие функции, например насыщающий гиперболический тангенс. $f(x)=\tanh(x)$, $f(x)=|\tanh(x)|$и сигмовидная функция ${\textstyle \sigma (x)=(1+e^{-x})^{-1}}$. ReLU часто предпочтительнее других функций, поскольку он обучает нейронную сеть в несколько раз быстрее без значительного снижения точности обобщения .

Полностью связный слой

После нескольких сверточных слоев и слоев максимального пула окончательная классификация выполняется через полностью связанные слои. Нейроны в полностью связном слое имеют связи со всеми активациями предыдущего слоя, как это видно в обычных (несверточных) искусственных нейронных сетях . Таким образом, их активации можно вычислить как аффинное преобразование с умножением матрицы , за которым следует смещение смещения ( векторное сложение изученного или фиксированного термина смещения).

Слой потерь

Основные статьи: Функция потерь и Функции потерь для классификации.

«Уровень потерь» или « функция потерь » определяет, как обучение наказывает за отклонение между прогнозируемыми выходными данными сети и истинными метками данных (во время контролируемого обучения). различные функции потерь В зависимости от конкретной задачи могут использоваться .

Функция потерь Softmax используется для прогнозирования одного класса из K взаимоисключающих классов. Сигмовидная кросс-энтропийная потеря используется для прогнозирования K независимых значений вероятности в $[0,1]$. Евклидова потеря используется для регрессии к с действительным значением. меткам $(-\infty ,\infty )$.

Гиперпараметры

Гиперпараметры — это различные настройки, которые используются для управления процессом обучения. CNN используют больше гиперпараметров , чем стандартный многослойный перцептрон (MLP).

Размер ядра

Ядро — это количество пикселей, обработанных вместе. Обычно это выражается в размерах ядра, например, 2x2 или 3x3.

Заполнение

Заполнение — это добавление (обычно) пикселей со значением 0 на границах изображения. Это делается для того, чтобы граничные пиксели не были занижены (не потеряны) в выходных данных, поскольку обычно они участвуют только в одном экземпляре рецептивного поля. Применяемое дополнение обычно на единицу меньше соответствующего размера ядра. Например, сверточный слой, использующий ядра 3x3, получит 2-пиксельную площадку, то есть по 1 пикселю с каждой стороны изображения.

Страйд

Шаг — это количество пикселей, на которое окно анализа перемещается на каждой итерации. Шаг 2 означает, что каждое ядро ​​смещено на 2 пикселя относительно своего предшественника.

Количество фильтров

Поскольку размер карты объектов уменьшается с глубиной, слои рядом с входным слоем, как правило, имеют меньше фильтров, а более высокие слои могут иметь больше. Чтобы уравнять вычисления на каждом слое, произведение значений признаков v _a на положение пикселя поддерживается примерно постоянным на всех слоях. Для сохранения большего количества информации о входных данных потребуется, чтобы общее количество активаций (количество карт объектов, умноженное на количество позиций пикселей) не уменьшалось от одного слоя к другому.

Количество карт признаков напрямую влияет на емкость и зависит от количества доступных примеров и сложности задачи.

Размер фильтра

Общие размеры фильтров, встречающиеся в литературе, сильно различаются и обычно выбираются на основе набора данных.

Задача состоит в том, чтобы найти правильный уровень детализации, чтобы создавать абстракции в нужном масштабе с учетом конкретного набора данных и без переобучения .

Тип и размер пула

Обычно используется максимальное объединение , часто с размером 2x2. Это означает, что входные данные значительно уменьшаются , что снижает затраты на обработку.

Увеличение пула уменьшает размерность сигнала и может привести к неприемлемой потере информации . Зачастую лучше всего работают непересекающиеся окна пула.

Дилатация

Расширение предполагает игнорирование пикселей внутри ядра. Это потенциально уменьшает обработку/память без значительной потери сигнала. Расширение 2 в ядре 3x3 расширяет ядро ​​до 5x5, при этом все еще обрабатывается 9 (равномерно расположенных) пикселей. Соответственно, расширение 4 расширяет ядро ​​до 7x7.

и

Обычно предполагается, что CNN инвариантны к сдвигам входных данных. Слои свертки или объединения внутри CNN, шаг которых не превышает единицы, действительно эквивалентны переводам входных данных. Однако слои с шагом больше единицы игнорируют теорему выборки Найквиста-Шеннона и могут привести к искажению входного сигнала. Хотя в принципе CNN способны реализовывать фильтры сглаживания, было замечено, что на практике этого не происходит. и дают модели, которые не эквивариантны переводам.Более того, если CNN использует полносвязные слои, трансляционная эквивалентность не подразумевает трансляционную инвариантность, поскольку полносвязные слои не инвариантны к сдвигам входных данных. Одним из решений для полной инвариантности трансляции является отказ от понижающей выборки по всей сети и применение глобального среднего пула на последнем уровне. Кроме того, было предложено несколько других частичных решений, таких как сглаживание перед операциями понижения разрешения. пространственные трансформаторные сети, увеличение данных , подвыборка в сочетании с объединением в пулы, и капсульные нейронные сети .

Оценка

Точность окончательной модели основана на части набора данных, выделенной в начале и часто называемой тестовым набором. такие методы, как k -кратная перекрестная проверка В других случаях применяются . Другие стратегии включают использование конформного предсказания .

Методы регуляризации

Основная статья: Регуляризация (математика)

Регуляризация — это процесс введения дополнительной информации для решения некорректной задачи или предотвращения переобучения . CNN используют различные типы регуляризации.

Эмпирический

Выбывание

Поскольку полносвязный слой занимает большую часть параметров, он склонен к переобучению. Одним из методов уменьшения переобучения является дропаут , представленный в 2014 году. На каждом этапе обучения отдельные узлы либо «выпадают» из сети (игнорируются) с вероятностью $1-p$ или сохраняется с вероятностью $p$, так что остается уменьшенная сеть; входящие и исходящие ребра к выпавшему узлу также удаляются. На этом этапе на данных обучается только сокращенная сеть. Удаленные узлы затем повторно вставляются в сеть с их первоначальными весами.

На этапах обучения, $p$ обычно составляет 0,5; для входных узлов оно обычно намного выше, поскольку информация напрямую теряется, когда входные узлы игнорируются.

Во время тестирования после завершения обучения нам в идеале хотелось бы найти выборочное среднее всех возможных значений. $2^{n}$ выпавшие сети; к сожалению, это невозможно для больших значений $n$. Однако мы можем найти приближение, используя полную сеть, в которой выход каждого узла взвешивается с коэффициентом $p$, поэтому ожидаемое значение вывода любого узла такое же, как и на этапах обучения. Это самый большой вклад метода отсева: хотя он эффективно генерирует $2^{n}$ нейронных сетей и, как таковые, позволяют комбинировать модели, во время тестирования необходимо тестировать только одну сеть.

Избегая обучения всех узлов на всех обучающих данных, отсев уменьшает переобучение. Метод также значительно повышает скорость обучения. Это делает комбинацию моделей практичной даже для глубоких нейронных сетей . Кажется, что этот метод уменьшает взаимодействие узлов, что позволяет им изучать более надежные функции. лучше обобщить на новые данные.

ДропКоннект

DropConnect — это обобщение исключения, при котором с вероятностью может быть отброшено каждое соединение, а не каждый выходной блок. $1-p$. Таким образом, каждый блок получает входные данные от случайного подмножества блоков на предыдущем уровне.

DropConnect аналогичен исключению, поскольку он вводит динамическую разреженность в модели, но отличается тем, что разреженность связана с весами, а не с выходными векторами слоя. Другими словами, полностью связанный уровень с DropConnect становится разреженным слоем, в котором соединения выбираются случайным образом на этапе обучения.

Стохастический пул

Основным недостатком Dropout является то, что он не дает тех же преимуществ для сверточных слоев, где нейроны не полностью связаны.

Еще до Dropout, в 2013 году, была использована техника под названием стохастический пул. обычные детерминированные операции объединения были заменены стохастической процедурой, в которой активация в каждой области объединения выбирается случайным образом в соответствии с полиномиальным распределением , заданным действиями в пределах региона объединения. Этот подход не содержит гиперпараметров и может сочетаться с другими подходами к регуляризации, такими как исключение и увеличение данных .

Альтернативный взгляд на стохастическое объединение состоит в том, что оно эквивалентно стандартному максимальному объединению, но со многими копиями входного изображения, каждая из которых имеет небольшие локальные деформации . Это похоже на явные упругие деформации входных изображений: который обеспечивает превосходную производительность при работе с набором данных MNIST . Использование стохастического объединения в многослойной модели приводит к экспоненциальному числу деформаций, поскольку выборка в более высоких слоях не зависит от выборки в нижних слоях.

Искусственные данные

Основная статья: Увеличение данных

Поскольку степень переобучения модели определяется как ее мощностью, так и объемом обучения, которое она получает, предоставление сверточной сети большего количества обучающих примеров может уменьшить переобучение. Поскольку доступных данных для обучения зачастую недостаточно, особенно если учесть, что некоторую часть следует сохранить для последующего тестирования, есть два подхода: либо сгенерировать новые данные с нуля (если это возможно), либо изменить существующие данные для создания новых. Последний используется с середины 1990-х годов. Например, входные изображения можно обрезать, вращать или масштабировать для создания новых примеров с теми же метками, что и исходный обучающий набор.

Явное

Ранняя остановка

Основная статья: Ранняя остановка

Один из самых простых способов предотвратить переобучение сети — просто остановить обучение до того, как произойдет переобучение. Недостатком этого является то, что процесс обучения останавливается.

Количество параметров

Еще один простой способ предотвратить переоснащение — ограничить количество параметров, обычно путем ограничения количества скрытых модулей в каждом слое или ограничения глубины сети. Для сверточных сетей размер фильтра также влияет на количество параметров. Ограничение количества параметров напрямую ограничивает прогнозирующую способность сети, уменьшая сложность функции, которую она может выполнять с данными, и, таким образом, ограничивает количество переобучения. Это эквивалентно « нулевой норме ».

Снижение веса

Простая форма добавленного регуляризатора — это затухание веса, которое просто добавляет дополнительную ошибку, пропорциональную сумме весов ( норма L1 ) или квадрату величины ( норма L2 ) весового вектора, к ошибке в каждом узле. Уровень приемлемой сложности модели можно снизить, увеличив константу пропорциональности (гиперпараметр «альфа»), тем самым увеличив штраф за большие весовые векторы.

Регуляризация L2 — наиболее распространенная форма регуляризации. Это можно реализовать путем штрафования квадратов всех параметров непосредственно в цели. Регуляризация L2 имеет интуитивную интерпретацию, заключающуюся в строгом наказании пиковых весовых векторов и предпочтении диффузных весовых векторов. Из-за мультипликативного взаимодействия между весами и входными данными это имеет полезное свойство, побуждающее сеть использовать все свои входные данные понемногу, а не часто использовать некоторые из своих входных данных.

Регуляризация L1 также распространена. Это делает весовые векторы разреженными во время оптимизации. Другими словами, нейроны с регуляризацией L1 в конечном итоге используют только редкое подмножество своих наиболее важных входных данных и становятся почти инвариантными к зашумленным входным сигналам. Регуляризацию L1 и L2 можно комбинировать; это называется эластичной сетевой регуляризацией .

Максимальные ограничения нормы

Другая форма регуляризации — установить абсолютную верхнюю границу величины весового вектора для каждого нейрона и использовать прогнозируемый градиентный спуск для обеспечения соблюдения ограничения. На практике это соответствует обычному обновлению параметров, а затем обеспечению соблюдения ограничения путем фиксации весового вектора. ${\vec {w}}$ каждого нейрона для удовлетворения $\|{\vec {w}}\|_{2}<c$. Типичные значения $c$ имеют порядок 3–4. В некоторых статьях сообщается об улучшениях при использовании этой формы регуляризации.

Иерархические системы координат

При объединении теряются точные пространственные отношения между частями высокого уровня (такими как нос и рот на изображении лица). Эти отношения необходимы для распознавания личности. Перекрытие пулов, так что каждый объект встречается в нескольких пулах, помогает сохранить информацию. Сам по себе перевод не может экстраполировать понимание геометрических отношений на радикально новую точку зрения, например, на другую ориентацию или масштаб. С другой стороны, люди очень хорошо умеют экстраполировать; увидев новую форму, они смогут распознать ее с другой точки зрения.

Более ранний распространенный способ решения этой проблемы — обучение сети на преобразованных данных в разных ориентациях, масштабах, освещении и т. д., чтобы сеть могла справиться с этими изменениями. Это требует больших вычислительных ресурсов для больших наборов данных. Альтернативой является использование иерархии систем координат и использование группы нейронов для представления сочетания формы объекта и его положения относительно сетчатки . Поза относительно сетчатки — это взаимосвязь между системой координат сетчатки и системой координат внутренних особенностей.

Таким образом, один из способов представить что-либо — это встроить в него систему координат. Это позволяет распознавать крупные черты лица, используя согласованность поз их частей (например, позы носа и рта позволяют последовательно прогнозировать позу всего лица). Этот подход гарантирует, что объект более высокого уровня (например, лицо) присутствует, когда объект более низкого уровня (например, нос и рот) соглашается с прогнозом позы. Векторы активности нейронов, представляющие позу («векторы позы»), позволяют осуществлять пространственные преобразования, смоделированные как линейные операции, которые облегчают сети изучение иерархии визуальных объектов и обобщение точек зрения. Это похоже на то, как зрительная система человека накладывает рамки координат для представления форм.

Приложения

Распознавание изображений

CNN часто используются в системах распознавания изображений . В 2012 году о частоте ошибок 0,23% . в базе данных MNIST сообщалось В другой статье об использовании CNN для классификации изображений сообщается, что процесс обучения был «на удивление быстрым»; в той же статье лучшие опубликованные результаты по состоянию на 2011 год были достигнуты в базе данных MNIST и базе данных NORB. Впоследствии аналогичный CNN назвал АлексНет выиграл конкурс ImageNet по крупномасштабному визуальному распознаванию 2012.

Применительно к распознаванию лиц CNN добились значительного снижения частоты ошибок. В другой статье сообщалось о 97,6% распознавании «5600 неподвижных изображений более 10 предметов». CNN использовались для оценки качества видео объективной после ручного обучения; полученная система имела очень низкую среднеквадратическую ошибку .

— Масштабный конкурс визуального распознавания ImageNet это эталон в классификации и обнаружении объектов, в котором участвуют миллионы изображений и сотни классов объектов. На ILSVRC 2014 г. В ходе масштабной задачи по визуальному распознаванию почти каждая команда с высоким рейтингом использовала CNN в качестве базовой структуры. Победитель ГуглЛеНет (основа DeepDream ) увеличил среднюю точность обнаружения объектов до 0,439329 и снизил ошибку классификации до 0,06656, что является лучшим результатом на сегодняшний день. В его сети применено более 30 слоев. Производительность сверточных нейронных сетей в тестах ImageNet была близка к показателям людей. Лучшие алгоритмы по-прежнему борются с маленькими или тонкими объектами, такими как маленький муравей на стебле цветка или человек, держащий в руке перо. У них также возникают проблемы с изображениями, искаженными фильтрами, что является все более распространенным явлением в современных цифровых камерах. Напротив, подобные изображения редко беспокоят людей. Однако у людей обычно возникают проблемы с другими проблемами. Например, они не умеют классифицировать объекты по детальным категориям, таким как конкретная порода собаки или вид птицы, тогда как сверточные нейронные сети справляются с этим.

В 2015 году многослойная CNN продемонстрировала способность распознавать лица под разными углами, в том числе перевернутыми, даже при частичном закрытии, с конкурентоспособными характеристиками. Сеть была обучена на базе данных из 200 000 изображений, включающих лица под разными углами и ориентациями, а также еще 20 миллионов изображений без лиц. Они использовали пакеты по 128 изображений в течение 50 000 итераций.

Видеоанализ

По сравнению с доменами данных изображений, работы по применению CNN для классификации видео относительно мало. Видео сложнее изображений, поскольку оно имеет другое (временное) измерение. Тем не менее, были изучены некоторые расширения CNN в область видео. Один из подходов состоит в том, чтобы рассматривать пространство и время как эквивалентные измерения входных данных и выполнять свертки как во времени, так и в пространстве. Другой способ — объединить функции двух сверточных нейронных сетей: одной для пространственного, а другой для временного потока. единицы долгосрочной краткосрочной памяти (LSTM) Рекуррентные обычно включаются после CNN для учета зависимостей между кадрами или между клипами. неконтролируемого обучения Были представлены схемы для обучения пространственно-временных функций, основанные на сверточных вентилируемых ограниченных машинах Больцмана. и независимый анализ подпространства. Его применение можно увидеть в модели преобразования текста в видео .

Обработка естественного языка

CNN также использовались для обработки естественного языка . Модели CNN эффективны для решения различных задач НЛП и достигли отличных результатов в семантическом анализе . получение поисковых запросов, моделирование предложений, классификация, прогноз и другие традиционные задачи НЛП. По сравнению с традиционными методами языковой обработки, такими как рекуррентные нейронные сети , CNN могут представлять различные контекстуальные реалии языка, которые не полагаются на предположение о последовательностях рядов, в то время как RNN лучше подходят, когда требуется классическое моделирование временных рядов.

Обнаружение аномалий

CNN с одномерными свертками использовалась во временных рядах в частотной области (спектральный остаток) с помощью неконтролируемой модели для обнаружения аномалий во временной области.

Открытие лекарств

CNN использовались при открытии лекарств . Прогнозирование взаимодействия между молекулами и биологическими белками может определить потенциальные методы лечения. В 2015 году Atomwise представила AtomNet, первую нейронную сеть глубокого обучения для разработки лекарств на основе структуры . Система обучается непосредственно на трехмерных представлениях химических взаимодействий. Подобно тому, как сети распознавания изображений учатся объединять меньшие, пространственно близкие объекты в более крупные и сложные структуры. AtomNet обнаруживает химические свойства, такие как ароматичность , sp. ³ углерода и водородной связи . Впоследствии AtomNet использовалась для прогнозирования новых биомолекул- кандидатов для лечения множества заболеваний, в первую очередь для лечения вируса Эбола. и рассеянный склероз .

Игра в шашки

CNN использовались в игре в шашки . С 1999 по 2001 год Фогель и Челлапилла опубликовали статьи, показывающие, как сверточная нейронная сеть может научиться играть в шашку, используя коэволюцию. В процессе обучения не использовались предыдущие человеческие профессиональные игры, а, скорее, основное внимание уделялось минимальному набору информации, содержащейся в шахматной доске: расположению и типу фигур, а также разнице в количестве фигур на двух сторонах. В конечном итоге программа ( Blondie24 ) была протестирована на 165 играх против игроков и заняла высшие 0,4%. Он также одержал победу над программой Chinook на ее «экспертном» уровне игры.

Иди

CNN использовались в компьютерном Go . В декабре 2014 года Кларк и Сторки опубликовали статью, показывающую, что CNN, обученная контролируемым обучением на основе базы данных профессиональных игр людей, может превзойти GNU Go и выиграть несколько игр против поиска по дереву Монте-Карло Fuego 1.1 за долю времени, которое потребовалось Fuego играть. Позже было объявлено, что большая 12-слойная сверточная нейронная сеть правильно предсказала профессиональный ход в 55% позиций, что соответствует точности игрока-человека с 6 даном . Когда обученная сверточная сеть использовалась непосредственно для игр в Го, без какого-либо поиска, она превзошла традиционную программу поиска GNU Go в 97% игр и сравнялась по производительности с программой поиска по дереву Монте-Карло Fuego, имитирующей десять тысяч игр (около миллион позиций) за ход.

использовала пару CNN для выбора ходов («политическая сеть») и оценки позиций («сеть ценности»), управляющих MCTS AlphaGo , которая первой обыграла лучшего игрока-человека того времени.

временных

Рекуррентные нейронные сети обычно считаются лучшими архитектурами нейронных сетей для прогнозирования временных рядов (и моделирования последовательностей в целом), но недавние исследования показывают, что сверточные сети могут работать сопоставимо или даже лучше. Расширенные извилины может позволить одномерным сверточным нейронным сетям эффективно изучать зависимости временных рядов. Свертки могут быть реализованы более эффективно, чем решения на основе RNN, и они не страдают от исчезновения (или взрыва) градиентов. Сверточные сети могут обеспечить повышенную эффективность прогнозирования, когда имеется несколько похожих временных рядов, на которых можно учиться. CNN также можно применять для дальнейших задач анализа временных рядов (например, классификации временных рядов). или квантильное прогнозирование ).

Культурное наследие и наборы

Поскольку археологические находки, такие как глиняные таблички с клинописью, все чаще приобретаются с помощью 3D-сканеров , становятся доступными наборы эталонных данных, включая HeiCuBeDa. предоставление почти 2000 нормализованных наборов 2-D и 3-D данных, подготовленных с помощью GigaMesh Software Framework . Таким образом, измерения на основе кривизны используются в сочетании с геометрическими нейронными сетями (GNN), например, для классификации периода тех глиняных табличек, которые являются одними из древнейших документов истории человечества.

Тонкая настройка

Для многих приложений данные обучения не очень доступны. Сверточные нейронные сети обычно требуют большого объема обучающих данных, чтобы избежать переобучения . Распространенным методом является обучение сети на большем наборе данных из связанной области. После того, как параметры сети сошлись, выполняется дополнительный этап обучения с использованием внутридоменных данных для точной настройки весов сети. Это называется трансферным обучением . Более того, этот метод позволяет успешно применять архитектуры сверточных сетей для решения задач с крошечными обучающими наборами.

Объяснения

Сквозное обучение и прогнозирование — обычная практика в компьютерном зрении . , требуются понятные человеку объяснения Однако для таких критически важных систем , как беспилотные автомобили . Благодаря недавним достижениям в области визуальной значимости , пространственного и временного внимания , наиболее важные пространственные области/временные моменты могут быть визуализированы, чтобы оправдать предсказания CNN.

Связанные архитектуры

Глубокие Q-сети

Глубокая Q-сеть (DQN) — это тип модели глубокого обучения, которая сочетает в себе глубокую нейронную сеть с Q-обучением , формой обучения с подкреплением . В отличие от более ранних агентов обучения с подкреплением, DQN, использующие CNN, могут учиться непосредственно на многомерных сенсорных входных данных посредством обучения с подкреплением.

Предварительные результаты были представлены в 2014 году, а сопроводительный документ — в феврале 2015 года. В исследовании описано применение игр для Atari 2600 . Этому предшествовали другие модели глубокого обучения с подкреплением.

Сети

Основная статья: Сеть глубоких убеждений

Сверточные сети глубокого убеждения (CDBN) имеют структуру, очень похожую на сверточные нейронные сети, и обучаются аналогично сетям глубокого убеждения. Поэтому они используют двумерную структуру изображений, как это делают CNN, и используют предварительное обучение, например, сети глубокого убеждения . Они предоставляют общую структуру, которую можно использовать во многих задачах обработки изображений и сигналов. Результаты сравнительного анализа стандартных наборов данных изображений, таких как CIFAR. были получены с использованием CDBN.

Известные библиотеки

• Caffe : библиотека для сверточных нейронных сетей. Создано Центром видения и обучения Беркли (BVLC). Он поддерживает как процессор, так и графический процессор. Разработан на C++ и имеет Python и MATLAB . оболочки
• Deeplearning4j : глубокое обучение Java и Scala с поддержкой нескольких графических процессоров в Spark . Библиотека глубокого обучения общего назначения для производственного стека JVM, работающая на движке научных вычислений C++. Позволяет создавать собственные слои. Интегрируется с Hadoop и Kafka.
• Dlib : набор инструментов для создания реальных приложений машинного обучения и анализа данных на C++.
• Microsoft Cognitive Toolkit : набор инструментов глубокого обучения, написанный Microsoft, с несколькими уникальными функциями, улучшающими масштабируемость на нескольких узлах. Он поддерживает полноценные интерфейсы для обучения C++ и Python, а также дополнительную поддержку вывода моделей на C# и Java.
• TensorFlow : Theano-подобная библиотека под лицензией Apache 2.0 Google с поддержкой CPU, GPU, собственного тензорного процессора (TPU), и мобильные устройства.
• Theano : эталонная библиотека глубокого обучения для Python с API, в значительной степени совместимым с популярной библиотекой NumPy . Позволяет пользователю писать символические математические выражения, а затем автоматически генерирует их производные, избавляя пользователя от необходимости кодировать градиенты или обратное распространение ошибки. Эти символические выражения автоматически компилируются в код CUDA для быстрой реализации на графическом процессоре .
• Torch : среда научных вычислений с широкой поддержкой алгоритмов машинного обучения, написанная на C и Lua .

См. также

• Внимание (машинное обучение)
• Свертка
• Глубокое обучение
• Обработка естественного языка
• Неокогнитрон
• Преобразование масштабно-инвариантного объекта
• Нейронная сеть с задержкой времени
• Блок обработки изображений

Внешние ссылки

• CS231n: Сверточные нейронные сети для визуального распознавания — зрении Стэнфордский компьютерном курс информатики Андрея Карпати по CNN в