Сеть глубоких убеждений

Схематический обзор глубокой сети убеждений. Стрелки обозначают направленные соединения в графической модели , которую представляет сеть.

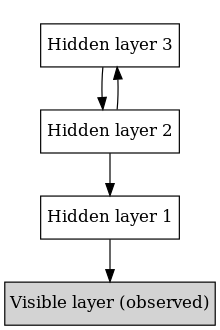
В машинном обучении сеть глубоких убеждений ( DBN ) представляет собой генеративную графическую модель или, альтернативно, класс глубокой нейронной сети , состоящей из нескольких слоев скрытых переменных («скрытых единиц») со связями между слоями, но не между единицами внутри. каждый слой.

При обучении на наборе примеров без присмотра DBN может научиться вероятностно реконструировать свои входные данные. Затем слои действуют как детекторы объектов . После этого этапа обучения DBN можно дополнительно обучить под наблюдением выполнению классификации .

DBN можно рассматривать как совокупность простых неконтролируемых сетей, таких как ограниченные машины Больцмана (RBM). или автоэнкодеры , где скрытый слой каждой подсети служит видимым слоем для следующей. RBM — это ненаправленная генеративная модель, основанная на энергии, с «видимым» входным слоем и скрытым слоем, а также связями между слоями, но не внутри них. Такая композиция приводит к быстрой, послойной неконтролируемой процедуре обучения, где контрастная дивергенция применяется к каждой подсети по очереди, начиная с «самой нижней» пары слоев (самый нижний видимый слой — это обучающий набор ).

Наблюдение Тот факт, что DBN можно обучать жадно , по одному уровню за раз, привел к созданию одного из первых эффективных алгоритмов глубокого обучения . В целом, существует множество привлекательных реализаций и применений DBN в реальных приложениях и сценариях (например, электроэнцефалография , открытие лекарств ).

Обучение

Метод обучения RBM, предложенный Джеффри Хинтоном для использования с моделями обучения « Продукт экспертов », называется контрастивной дивергенцией (CD). CD обеспечивает приближение к методу максимального правдоподобия , который в идеале можно было бы применять для изучения весов. При обучении одного RBM обновления веса выполняются с градиентным спуском по следующему уравнению: $w_{ij}(t+1)=w_{ij}(t)+\eta {\frac {\partial \log(p(v))}{\partial w_{ij}}}$

где, $p(v)$ - вероятность видимого вектора, которая определяется выражением $p(v)={\frac {1}{Z}}\sum _{h}e^{-E(v,h)}$. $Z$ - функция распределения (используется для нормализации) и $E(v,h)$ – энергетическая функция, присвоенная состоянию сети. Более низкая энергия указывает на то, что сеть находится в более «желательной» конфигурации. Градиент ${\frac {\partial \log(p(v))}{\partial w_{ij}}}$ имеет простую форму $\langle v_{i}h_{j}\rangle _{\text{data}}-\langle v_{i}h_{j}\rangle _{\text{model}}$ где $\langle \cdots \rangle _{p}$ представляют собой средние значения по отношению к распределению $p$. Проблема возникает при выборке $\langle v_{i}h_{j}\rangle _{\text{model}}$ поскольку для этого требуется расширенная попеременная выборка Гиббса . CD заменяет этот шаг, запуская попеременную выборку Гиббса для $n$ шаги (значения $n=1$ хорошо выступаем). После $n$ шагов, данные отбираются, и эта выборка используется вместо $\langle v_{i}h_{j}\rangle _{\text{model}}$. Процедура CD работает следующим образом:

1. Инициализируйте видимые единицы обучающим вектором.
2. Обновите скрытые блоки параллельно с видимыми блоками: $p(h_{j}=1\mid {\textbf {V}})=\sigma (b_{j}+\sum _{i}v_{i}w_{ij})$. $\sigma$ сигмовидная функция и $b_{j}$ это предвзятость $h_{j}$.
3. Обновите видимые модули параллельно с учетом скрытых модулей: $p(v_{i}=1\mid {\textbf {H}})=\sigma (a_{i}+\sum _{j}h_{j}w_{ij})$. $a_{i}$ это предвзятость $v_{i}$. Это называется этапом «реконструкции».
4. Повторно обновите скрытые единицы параллельно с учетом реконструированных видимых единиц, используя то же уравнение, что и на шаге 2.
5. Выполните обновление веса: $\Delta w_{ij}\propto \langle v_{i}h_{j}\rangle _{\text{data}}-\langle v_{i}h_{j}\rangle _{\text{reconstruction}}$.

После обучения RBM поверх него «накладывается» другой RBM, получающий входные данные от последнего обученного слоя. Новый видимый слой инициализируется обучающим вектором, а значения единиц в уже обученных слоях присваиваются с использованием текущих весов и смещений. Затем новый RBM обучается с помощью описанной выше процедуры. Весь этот процесс повторяется до тех пор, пока не будет достигнут желаемый критерий остановки.

Хотя приближение CD к максимальному правдоподобию является грубым (не соответствует градиенту какой-либо функции), оно эмпирически эффективно.

Ограниченная машина Больцмана (RBM) с полностью подключенными видимыми и скрытыми блоками. Обратите внимание, что здесь нет скрыто-скрытых или видимо-видимых связей.

См. также

• Байесовская сеть
• Сверточная сеть глубоких убеждений
• Глубокое обучение
• Энергетическая модель
• Многоуровневая ограниченная машина Больцмана

Внешние ссылки

• «Сети глубоких убеждений» . Учебники по глубокому обучению.
• «Пример сети глубоких убеждений» . Учебники по Deeplearning4j. Архивировано из оригинала 3 октября 2016 г. Проверено 22 февраля 2015 г.