Ленет

LeNet — это структура сверточной нейронной сети, предложенная ЛеКуном и др. в 1998 году. [1] В целом LeNet относится к LeNet-5 и представляет собой простую сверточную нейронную сеть . Сверточные нейронные сети — это своего рода нейронная сеть прямого распространения , искусственные нейроны которой могут реагировать на часть окружающих ячеек в диапазоне покрытия и хорошо работать при крупномасштабной обработке изображений.
История развития
[ редактировать ]LeNet-5 была одной из первых сверточных нейронных сетей и способствовала развитию глубокого обучения . С 1988 года, после многих лет исследований и множества успешных итераций, новаторская работа получила название LeNet-5.

В 1989 году Ян ЛеКун и др. в Bell Labs впервые применили алгоритм обратного распространения ошибки к практическим приложениям и полагали, что способность к обучению обобщению сети можно значительно улучшить, предоставив ограничения из предметной области задачи. Он объединил сверточную нейронную сеть, обученную алгоритмами обратного распространения ошибки для чтения рукописных чисел, и успешно применил ее для идентификации рукописных номеров почтовых индексов, предоставленных Почтовой службой США . Это был прототип того, что позже стало называться LeNet. [2] В том же году ЛеКун описал небольшую проблему распознавания рукописных цифр в другой статье и показал, что, хотя проблема линейно разделима, однослойные сети демонстрируют плохие возможности обобщения. При использовании детекторов признаков, инвариантных к сдвигу, в многослойной сети с ограничениями модель может работать очень хорошо. Он считал, что эти результаты доказывают, что минимизация количества свободных параметров в нейронной сети может повысить способность нейронной сети к обобщению. [3]
В 1990 году в их статье снова было описано применение сетей обратного распространения ошибки для распознавания рукописных цифр. Они выполнили лишь минимальную предварительную обработку данных, а модель была тщательно разработана для этой задачи и имела строгие ограничения. Входные данные состояли из изображений, каждое из которых содержало число, а результаты тестирования цифровых данных почтового индекса, предоставленные Почтовой службой США, показали, что уровень ошибок модели составлял всего 1%, а уровень отклонения — около 9%. [4]
Их исследования продолжались следующие четыре года, и в 1994 году была разработана база данных MNIST , для которой LeNet-1 была слишком мала, поэтому на ней была обучена новая NN LeNet-4. [5] Год спустя коллектив AT&T Bell Labs представил LeNet-5 и рассмотрел различные методы распознавания рукописных символов на бумаге, используя стандартные рукописные цифры для определения эталонных задач. Эти модели были сравнены, и результаты показали, что последняя сеть превзошла другие модели. [6] К 1998 году Ян ЛеКун, Леон Ботту , Йошуа Бенджио и Патрик Хаффнер смогли предоставить примеры практического применения нейронных сетей, такие как две системы для распознавания рукописных символов в Интернете и модели, способные считывать миллионы чеков в день. [1]
Исследования достигли больших успехов и вызвали интерес учёных к изучению нейронных сетей. Хотя архитектура наиболее эффективных сегодня нейронных сетей не такая же, как у LeNet, сеть стала отправной точкой для большого количества архитектур нейронных сетей, а также вдохновила эту область.
| 1989 | Янн ЛеКун и др. предложил первоначальную форму LeNet | ЛеКун, Ю.; Бозер, Б.; Денкер, Дж.С.; Хендерсон, Д.; Ховард, RE; Хаббард, В. и Джекель, Л.Д. (1989). Обратное распространение применяется к распознаванию рукописного почтового индекса. Нейронные вычисления, 1(4):541-551. [2] |
| 1989 | Ян ЛеКун доказывает, что минимизация количества свободных параметров в нейронных сетях может повысить способность нейронных сетей к обобщению. | ЛеКун, Ю. (1989). Стратегии обобщения и сетевого проектирования. Технический отчет CRG-TR-89-4, факультет компьютерных наук, Университет Торонто. [3] |
| 1990 | В их статье еще раз описывается применение сетей обратного распространения ошибки в распознавании рукописных цифр. | ЛеКун, Ю.; Бозер, Б.; Денкер, Дж.С.; Хендерсон, Д.; Ховард, RE; Хаббард, В. и Джекель, Л.Д. (1990). Распознавание рукописных цифр с помощью сети обратного распространения ошибки. Достижения в области нейронных систем обработки информации 2 (NIPS * 89). [4] |
| 1994 | Разработана база данных MNIST и LeNet-4. | |
| 1995 | Разработан LeNet-5, различные методы, применяемые для распознавания рукописных символов, рассмотрены и сравнены со стандартными тестами распознавания рукописных цифр. Результаты показывают, что сверточные нейронные сети превосходят все другие модели. | |
| 1998 | Практическое применение | ЛеКун, Ю.; Ботту, Л.; Бенджио Ю. и Хаффнер П. (1998). Градиентное обучение применительно к распознаванию документов. Труды IEEE. 86(11): 2278-2324. [1] |
Структура
[ редактировать ]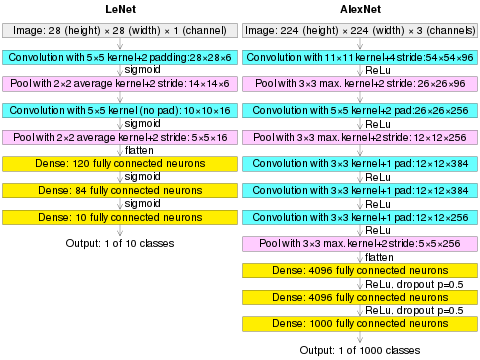
(Размер изображения AlexNet должен быть 227×227×3, а не 224×224×3, чтобы математические расчеты были верными. В исходной статье были указаны другие цифры, но Андрей Карпати, бывший руководитель отдела компьютерного зрения в Tesla, сказал это должно быть 227×227×3 (он сказал, что Алекс не объяснил, почему он поставил 224×224×3. Следующая свертка должна быть 11×11 с шагом 4: 55×55×96 (вместо 54×54×96). ). Это будет рассчитываться, например, как: [(входная ширина 227 - ширина ядра 11) / шаг 4] + 1 = [(227 - 11) / 4] + 1 = 55. Поскольку выходные данные ядра одинаковы. длина равна ширине, его площадь 55х55.)
Как представитель ранней сверточной нейронной сети, LeNet обладает основными модулями сверточной нейронной сети, такими как сверточный слой, слой пула и уровень полного соединения, что закладывает основу для будущего развития сверточной нейронной сети. Как показано на рисунке (входные данные изображения размером 32*32 пикселя): LeNet-5 состоит из семи слоев. Помимо ввода, каждый второй уровень может обучать параметры . На рисунке Cx представляет уровень свертки, Sx представляет уровень подвыборки, Fx представляет собой полный уровень соединения, а x представляет индекс слоя. [2] [7] [8]
Слой C1 представляет собой слой свертки с шестью ядрами свертки размером 5x5 и размером отображения объектов 28x28, что может предотвратить выпадение информации входного изображения за границу ядра свертки.
Слой S2 — это слой подвыборки/объединения, который выводит 6 графиков объектов размером 14x14. Каждая ячейка на каждой карте объектов соединена с окрестностями 2x2 на соответствующей карте объектов в C1.
Слой C3 представляет собой слой свертки с 16 ядрами свертки 5-5. Ввод первых шести карт признаков C3 представляет собой каждое непрерывное подмножество трех карт признаков в S2, вход следующих шести карт признаков поступает из входных данных четырех непрерывных подмножеств, а вход следующих трех карт признаков поступает из четыре разрывных подмножества. Наконец, входные данные для последнего графа признаков поступают из всех графов признаков S2.
Слой S4 аналогичен S2, имеет размер 2x2 и выводит 16 графиков функций 5x5.
Слой C5 — это слой свертки со 120 ядрами свертки размером 5x5. Каждая ячейка соединена с окрестностью 5*5 на всех 16 графах признаков S4. Здесь, поскольку размер графа функций S4 также равен 5x5, выходной размер C5 равен 1*1. Итак, S4 и C5 полностью связаны. C5 помечен как сверточный слой, а не как полностью связный слой, потому что, если входные данные LeNet-5 станут больше, а его структура останется неизменной, его выходной размер будет больше 1x1, т. е. не будет полностью связным слоем.
Слой F6 полностью подключен к C5, и выводятся 84 графа объектов.
Функции
[ редактировать ]- Каждый сверточный слой состоит из трех частей: функции свертки, объединения и нелинейной активации.
- Использование свертки для извлечения пространственных объектов (первоначально свертка называлась рецептивными полями)
- Средний слой подвыборки подвыборки
- Тана функция активации
- Использование MLP в качестве последнего классификатора
- Разреженные соединения между слоями для уменьшения сложности вычислений.
Приложение
[ редактировать ]Распознавание простых цифровых изображений — самое классическое приложение LeNet, поскольку оно было создано именно для этого.
Янн ЛеКун и др. создал первоначальную форму LeNet в 1989 году. Статья « Обратное распространение ошибки, примененная к распознаванию рукописного почтового индекса». [2] демонстрирует, как такие ограничения могут быть интегрированы в сеть обратного распространения ошибки через архитектуру сети. И он был успешно применен для распознавания рукописных цифр почтового индекса, предоставленных Почтовой службой США. [2]
Анализ развития
[ редактировать ]LeNet-5 означает появление CNN и определяет основные компоненты CNN . [1] Но в то время он не был популярен из-за отсутствия аппаратного обеспечения, особенно графических процессоров и других алгоритмов, таких как SVM, которые могли достичь аналогичных эффектов или даже превзойти LeNet.
После успеха AlexNet в 2012 году CNN стала лучшим выбором для приложений компьютерного зрения, и было создано множество различных типов CNN , например серия R- CNN . Сегодня модели CNN сильно отличаются от LeNet, но все они разработаны на основе LeNet.
Трехуровневая древовидная архитектура, имитирующая LeNet-5 и состоящая только из одного сверточного слоя, достигла аналогичного уровня успеха в наборе данных CIFAR-10. [9]
Увеличение количества фильтров для архитектуры LeNet приводит к степенному уменьшению частоты ошибок. Эти результаты показывают, что мелкая сеть может достичь той же производительности, что и архитектуры глубокого обучения. [10]
Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д Лекун, Ю.; Ботту, Л.; Бенджио, Ю.; Хаффнер, П. (1998). «Градиентное обучение, применяемое для распознавания документов» (PDF) . Труды IEEE . 86 (11): 2278–2324. дои : 10.1109/5.726791 . S2CID 14542261 .
- ^ Перейти обратно: а б с д и ЛеКун, Ю.; Бозер, Б.; Денкер, Дж.С.; Хендерсон, Д.; Ховард, RE; Хаббард, В.; Джекель, LD (декабрь 1989 г.). «Обратное распространение ошибки, примененное к распознаванию рукописного почтового индекса». Нейронные вычисления . 1 (4): 541–551. дои : 10.1162/neco.1989.1.4.541 . ISSN 0899-7667 . S2CID 41312633 .
- ^ Перейти обратно: а б Лекун, Янн (июнь 1989 г.). «Стратегии обобщения и сетевого проектирования» (PDF) . Технический отчет CRG-TR-89-4 . Департамент компьютерных наук Университета Торонто.
- ^ Перейти обратно: а б ЛеКун, Ю.; Бозер, Б.; Денкер, Дж.С.; Хендерсон, Д.; Ховард, RE; Хаббард, В.; Джекер, LD (июнь 1990 г.). «Распознавание рукописных цифр с помощью сети обратного распространения ошибки» (PDF) . Достижения в области нейронных систем обработки информации . 2 : 396–404.
- ^ http://yann.lecun.com/exdb/publis/pdf/bottou-94.pdf
- ^ https://www.eecis.udel.edu/~shatkay/Course/papers/NetworksAndCNNClasifiersIntroVapnik95.pdf
- ^ «LeNet of Convolutional Neural Network — Brook_icv — Blog Park» . www.cnblogs.com (на китайском языке (Китай)) Проверено 16 ноября 2019 г ..
- ^ «Подробное объяснение сверточной нейронной сети CNN глубокого обучения LeNet-5» . blog.csdn.net (на китайском языке (Китай)) . Проверено 16 ноября 2019 г.
- ^ Меир, Юваль; Бен-Ноам, Итамар; Цах, Ярден; Ходассман, Шири; Кантер, Идо (30 января 2023 г.). «Обучение древовидной архитектуре превосходит сверточную сеть прямого распространения» . Научные отчеты . 13 (1): 962. Бибкод : 2023НатСР..13..962М . дои : 10.1038/s41598-023-27986-6 . ISSN 2045-2322 . ПМЦ 9886946 . ПМИД 36717568 .
- ^ Меир, Юваль; Тевет, Офек; Цах, Ярден; Ходассман, Шири; Гросс, Ронит Д.; Кантер, Идо (20 апреля 2023 г.). «Эффективное поверхностное обучение как альтернатива глубокому обучению» . Научные отчеты . 13 (1): 5423. arXiv : 2211.11106 . Бибкод : 2023НатСР..13.5423М . дои : 10.1038/s41598-023-32559-8 . ISSN 2045-2322 . ПМЦ 10119101 . ПМИД 37080998 .