Функция активации

Функция активации узла в искусственной нейронной сети — это функция, которая вычисляет выходные данные узла на основе его отдельных входов и их весов. Нетривиальные задачи можно решить, используя всего несколько узлов, если функция активации нелинейна . ^[1] Современные функции активации включают плавную версию ReLU , GELU, которая использовалась в модели BERT 2018 года , ^[2] логистическая ( сигмовидная ) функция, используемая в модели распознавания речи 2012 года , разработанной Хинтоном и др., ^[3] ReLU , используемый в AlexNet 2012 года. модели компьютерного зрения ^[4]^[5] и в модели ResNet 2015 года .

Сравнение функций активации [ править ]

Помимо эмпирических характеристик, функции активации также обладают различными математическими свойствами:

Нелинейный: Когда функция активации нелинейна, можно доказать, что двухслойная нейронная сеть является универсальным аппроксиматором функции. ^[6]Это известно как Теорема универсального приближения . Функция активации идентичности не удовлетворяет этому свойству. Когда несколько уровней используют функцию активации идентификации, вся сеть эквивалентна одноуровневой модели.
Диапазон: Когда диапазон функции активации конечен, методы обучения на основе градиента имеют тенденцию быть более стабильными, поскольку представление шаблонов существенно влияет только на ограниченные веса. Когда диапазон бесконечен, обучение, как правило, более эффективно, поскольку представление шаблонов существенно влияет на большую часть весов. В последнем случае меньшие скорости обучения . обычно необходимы ^{[ нужна цитата ]}
Непрерывно дифференцируемый: Это свойство желательно ( ReLU не является непрерывно дифференцируемым и имеет некоторые проблемы с оптимизацией на основе градиента, но это все же возможно) для включения методов оптимизации на основе градиента. Функция активации двоичного шага не дифференцируема при 0 и дифференцируется до 0 для всех других значений, поэтому методы на основе градиента не могут добиться с ней прогресса. ^[7]

Эти свойства не оказывают решающего влияния на производительность и не являются единственными математическими свойствами, которые могут быть полезны. Например, строго положительный диапазон softplus делает его пригодным для прогнозирования отклонений в вариационных автоэнкодерах .

Математические детали [ править ]

Наиболее распространенные функции активации можно разделить на три категории: функции гребня , радиальные функции и функции складки .

Функция активации $f$ насыщает , если $\lim _{|v|\to \infty }|\nabla f(v)|=0$ . Оно ненасыщающее , если оно не насыщает. Ненасыщающие функции активации, такие как ReLU , могут быть лучше, чем насыщающие функции активации, поскольку они с меньшей вероятностью страдают от проблемы исчезающего градиента . ^[8]

Функции активации хребта [ править ]

Ридж-функции — это многомерные функции, действующие на линейную комбинацию входных переменных. Часто используемые примеры включают в себя: ^{[ нужны разъяснения ]}

Линейная активация: $\phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b}$ ,
Активация ReLU : $\phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )$ ,
Активация Хевисайда : $\phi (\mathbf {v} )=1_{a+\mathbf {v} '\mathbf {b} >0}$ ,
Логистическая активация: $\phi (\mathbf {v} )=(1+\exp(-a-\mathbf {v} '\mathbf {b} ))^{-1}$ .

В биологических нейронных сетях функция активации обычно представляет собой абстракцию, представляющую скорость срабатывания потенциала действия в клетке. ^[9]В своей простейшей форме эта функция является бинарной , то есть либо нейрон срабатывает, либо нет. Нейроны также не могут срабатывать быстрее определенной частоты, что мотивирует функции активации сигмовидной мышцы , диапазон которых составляет конечный интервал.

Функция выглядит как $\phi (\mathbf {v} )=U(a+\mathbf {v} '\mathbf {b} )$ , где $U$ – ступенчатая функция Хевисайда .

если линия имеет положительный наклон С другой стороны, , это может отражать увеличение скорости срабатывания, которое происходит по мере увеличения входного тока. Такая функция будет иметь вид $\phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b}$ .

Функции радиальной активации [ править ]

специальный класс функций активации, известный как радиальные базисные функции используется В RBF-сетях (RBF) , которые чрезвычайно эффективны в качестве универсальных аппроксиматоров функций. Эти функции активации могут принимать разные формы, но обычно они представляют собой одну из следующих функций:

Гауссово : $\,\phi (\mathbf {v} )=\exp \left(-{\frac {\|\mathbf {v} -\mathbf {c} \|^{2}}{2\sigma ^{2}}}\right)$
Мультиквадратика: $\,\phi (\mathbf {v} )={\sqrt {\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}}}$
Обратная мультиквадратика: $\,\phi (\mathbf {v} )=\left(\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}\right)^{-{\frac {1}{2}}}$
Полигармонические сплайны

где $\mathbf {c}$ вектор, представляющий центр функции и $a$ и $\sigma$ — параметры, влияющие на разброс радиуса.

Функции активации складывания [ править ]

Функции активации сворачивания широко используются в слоях объединения в сверточных нейронных сетях и в выходных слоях сетей многоклассовой классификации. Эти активации выполняют агрегирование входных данных, например, определение среднего , минимального или максимального значения . В мультиклассовой классификации softmax часто используется активация .

Таблица функций активации [ править ]

В следующей таблице сравниваются свойства нескольких функций активации, которые являются функциями одной складки $x$ предыдущего слоя или слоев:

Имя	Функция, $g(x)$	Производная от $g$ , $g'(x)$	Диапазон	Порядок преемственности
Личность	$x$	$1$	$(-\infty ,\infty )$	$C^{\infty }$
Бинарный шаг	${\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}$	$0$	$\{0,1\}$	$C^{-1}$
Логистический , сигмовидный или мягкий шаг	$\sigma (x)\doteq {\frac {1}{1+e^{-x}}}$	$g(x)(1-g(x))$	$(0,1)$	$C^{\infty }$
Гиперболический тангенс ( танх )	$\tanh(x)\doteq {\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	$1-g(x)^{2}$	$(-1,1)$	$C^{\infty }$
Soboleva modified hyperbolic tangent ( smht )	$\operatorname {smht} (x)\doteq {\frac {e^{ax}-e^{-bx}}{e^{cx}+e^{-dx}}}$		$(-1,1)$	$C^{\infty }$
Выпрямленный линейный агрегат (РеЛУ) ^[10]	${\begin{aligned}(x)^{+}\doteq {}&{\begin{cases}0&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}\\={}&\max(0,x)=x{\textbf {1}}_{x>0}\end{aligned}}$	${\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x>0\end{cases}}$	$[0,\infty )$	$C^{0}$
Линейная единица гауссовой ошибки (GELU) ^[2]	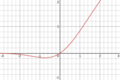${\begin{aligned}&{\frac {1}{2}}x\left(1+{\text{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right)\\{}={}&x\Phi (x)\end{aligned}}$	$\Phi (x)+x\phi (x)$	$(-0.17\ldots ,\infty )$	$C^{\infty }$
Софтплюс ^[11]	$\ln \left(1+e^{x}\right)$	${\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$
Экспоненциальный линейный блок (ЭЛУ) ^[12]	${\begin{cases}\alpha \left(e^{x}-1\right)&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}$ с параметром $\alpha$	${\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x>0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C^{1}&{\text{if }}\alpha =1\\C^{0}&{\text{otherwise}}\end{cases}}$
Масштабированный экспоненциальный линейный блок (SELU) ^[13]	$\lambda {\begin{cases}\alpha (e^{x}-1)&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}$ с параметрами $\lambda =1.0507$ и $\alpha =1.67326$	$\lambda {\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$
Выпрямленный линейный агрегат (Дырявый РеЛУ) ^[14]	${\begin{cases}0.01x&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}$	${\begin{cases}0.01&{\text{if }}x<0\\1&{\text{if }}x>0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$
Параметрический выпрямленный линейный блок (ПРеЛУ) ^[15]	${\begin{cases}\alpha x&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}$ с параметром $\alpha$	${\begin{cases}\alpha &{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$
Сигмовидный линейный блок (SiLU, ^[2] сморщивание сигмовидной кишки, ^[16] SiL, ^[17] или Свиш-‍1 ^[18])	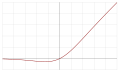${\frac {x}{1+e^{-x}}}$	${\frac {1+e^{-x}+xe^{-x}}{\left(1+e^{-x}\right)^{2}}}$	$[-0.278\ldots ,\infty )$	$C^{\infty }$
Гауссовский	$e^{-x^{2}}$	$-2xe^{-x^{2}}$	$(0,1]$	$C^{\infty }$

В следующей таблице перечислены функции активации, которые не являются функциями одного сгиба $x$ из предыдущего слоя или слоев:

Имя	Уравнение, $g_{i}\left({\vec {x}}\right)$	Производные , ${\frac {\partial g_{i}\left({\vec {x}}\right)}{\partial x_{j}}}$	Диапазон	Порядок преемственности
Софтмакс	${\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$ для $i$ = 1, …, $J$	$g_{i}\left({\vec {x}}\right)\left(\delta _{ij}-g_{j}\left({\vec {x}}\right)\right)$ ^[1]^[2]	$(0,1)$	$C^{\infty }$
Использовать полностью ^[19]	$\max _{i}x_{i}$	${\begin{cases}1&{\text{if }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{if }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

^ Здесь,

\delta _{ij}

это дельта Кронекера .

^ Например,

j

может перебирать количество ядер предыдущего слоя нейронной сети, в то время как

i

перебирает количество ядер текущего слоя.

функции активации Квантовые

В квантовых нейронных сетях с вентильной моделью , запрограммированных на квантовых компьютерах , основанных на квантовых перцептронах вместо вариационных квантовых схем, нелинейность функции активации может быть реализована без необходимости измерения выходного сигнала каждого перцептрона на каждом уровне. Квантовые свойства, загруженные в схему, такие как суперпозиция, могут быть сохранены путем создания ряда Тейлора аргумента, вычисленного самим персептроном, с подходящими квантовыми схемами, вычисляющими степени до желаемой степени аппроксимации. Благодаря гибкости таких квантовых схем их можно спроектировать так, чтобы аппроксимировать любую произвольную классическую функцию активации. ^[20]

См. также [ править ]

Ссылки [ править ]

^ Хинкельманн, Кнут. «Нейронные сети, стр. 7» (PDF) . Университет прикладных наук Северо-Западной Швейцарии . Архивировано из оригинала (PDF) 6 октября 2018 г. Проверено 6 октября 2018 г.
^ Перейти обратно: ^а ^б ^с Хендрикс, Дэн; Гимпел, Кевин (2016). «Линейные единицы гауссовой ошибки (GELU)». arXiv : 1606.08415 [ cs.LG ].
^ Хинтон, Джеффри; Дэн, Ли; Дэн, Ли; Ю, Донг; Даль, Джордж; Мохамед, Абдель-Рахман; Джейтли, Навдип; Старший, Эндрю; Ванхук, Винсент; Нгуен, Патрик; Сайнат, Тара ; Кингсбери, Брайан (2012). «Глубокие нейронные сети для акустического моделирования в распознавании речи». Журнал обработки сигналов IEEE . 29 (6): 82–97. дои : 10.1109/MSP.2012.2205597 . S2CID 206485943 .
^ Крижевский, Алекс; Суцкевер, Илья; Хинтон, Джеффри Э. (24 мая 2017 г.). «Классификация ImageNet с глубокими сверточными нейронными сетями» . Коммуникации АКМ . 60 (6): 84–90. дои : 10.1145/3065386 . ISSN 0001-0782 .
^ Университет короля Абдель Азиза; Аль-Джохания, Нора; Эльрефаи, Ламияа; Университет Бенха (30 июня 2019 г.). «Распознавание дорсальной вен руки с помощью сверточных нейронных сетей: подходы к обучению функциям и переносу обучения» (PDF) . Международный журнал интеллектуальной инженерии и систем . 12 (3): 178–191. дои : 10.22266/ijies2019.0630.19 .
^ Цыбенко, Г. (декабрь 1989 г.). «Приближение суперпозициями сигмоидальной функции» (PDF) . Математика управления, сигналов и систем . 2 (4): 303–314. дои : 10.1007/BF02551274 . ISSN 0932-4194 . S2CID 3958369 .
^ Снейман, Январь (3 марта 2005 г.). Практическая математическая оптимизация: введение в базовую теорию оптимизации, а также классические и новые градиентные алгоритмы . Springer Science & Business Media. ISBN 978-0-387-24348-1 .
^ Крижевский, Алекс; Суцкевер, Илья; Хинтон, Джеффри Э. (24 мая 2017 г.). «Классификация ImageNet с глубокими сверточными нейронными сетями» . Коммуникации АКМ . 60 (6): 84–90. дои : 10.1145/3065386 . ISSN 0001-0782 . S2CID 195908774 .
^ Ходжкин, Алабама; Хаксли, А. Ф. (28 августа 1952 г.). «Количественное описание мембранного тока и его применение к проводимости и возбуждению нерва» . Журнал физиологии . 117 (4): 500–544. doi : 10.1113/jphysicalol.1952.sp004764 . ПМК 1392413 . ПМИД 12991237 .
^ Наир, Винод; Хинтон, Джеффри Э. (2010), «Выпрямленные линейные единицы улучшают ограниченные машины Больцмана» , 27-я Международная конференция по машинному обучению , ICML'10, США: Omnipress, стр. 807–814, ISBN 9781605589077
^ Глорот, Ксавье; Борд, Антуан; Бенджио, Йошуа (2011). «Глубокие разреженные нейронные сети выпрямителя» (PDF) . Международная конференция по искусственному интеллекту и статистике .
^ Клеверт, Джорк-Арне; Унтертинер, Томас; Хохрайтер, Зепп (23 ноября 2015 г.). «Быстрое и точное глубокое сетевое обучение с помощью экспоненциальных линейных единиц (ELU)». arXiv : 1511.07289 [ cs.LG ].
^ Кламбауэр, Гюнтер; Унтертинер, Томас; Майр, Андреас; Хохрайтер, Зепп (08.06.2017). «Самонормализующиеся нейронные сети». Достижения в области нейронных систем обработки информации . 30 (2017). arXiv : 1706.02515 .
^ Маас, Эндрю Л.; Ханнун, Ауни Ю.; Нг, Эндрю Ю. (июнь 2013 г.). «Нелинейность выпрямителя улучшает акустические модели нейронных сетей». Учеб. ИКМЛ . 30 (1). S2CID 16489696 .
^ Каймин; Чжан, Сянюй; Рен, Шаоцин; Сунь, Цзянь (06 г. Хэ , февраля . 2015 )
^ Атто, Абдуррахман М.; Пастор Доминик; Мерсье, Грегуар (2008), «Плавное сжатие сигмовидного вейвлета для непараметрической оценки» (PDF) , Международная конференция IEEE по акустике, речи и обработке сигналов , 2008 г., стр. 3265–3268, doi : 10.1109/ICASSP.2008.4518347 , ISBN 978-1-4244-1483-3 , S2CID 9959057
^ Эльфвинг, Стефан; Учибе, Эйдзи; Дойя, Кенджи (2018). «Сигмовидные линейные единицы для аппроксимации функций нейронной сети при обучении с подкреплением». Нейронные сети . 107 : 3–11. arXiv : 1702.03118 . дои : 10.1016/j.neunet.2017.12.012 . ПМИД 29395652 . S2CID 6940861 .
^ Рамачандран, Праджит; Зоф, Баррет; Ле, Куок V (2017). «Поиск функций активации». arXiv : 1710.05941 [ cs.NE ].
^ Гудфеллоу, Ян Дж.; Вард-Фарли, Дэвид; Мирза, Мехди; Курвиль, Аарон; Бенджио, Йошуа (2013). «Максаут Нетворкс». Материалы семинара и конференции JMLR . 28 (3): 1319–1327. arXiv : 1302.4389 .
^ Маронезе, Марко; Дестри, Клаудио; Прати, Энрико (2022). «Квантовые функции активации для квантовых нейронных сетей». Квантовая обработка информации . 21 (4): 128. arXiv : 2201.03700 . Бибкод : 2022QuIP...21..128M . дои : 10.1007/s11128-022-03466-0 . ISSN 1570-0755 .

[1] Хинкельманн, Кнут. «Нейронные сети, стр. 7» (PDF) . Университет прикладных наук Северо-Западной Швейцарии . Архивировано из оригинала (PDF) 6 октября 2018 г. Проверено 6 октября 2018 г.

[ReferenceA-2] Перейти обратно: ^а ^б ^с Хендрикс, Дэн; Гимпел, Кевин (2016). «Линейные единицы гауссовой ошибки (GELU)». arXiv : 1606.08415 [ cs.LG ].

[3] Хинтон, Джеффри; Дэн, Ли; Дэн, Ли; Ю, Донг; Даль, Джордж; Мохамед, Абдель-Рахман; Джейтли, Навдип; Старший, Эндрю; Ванхук, Винсент; Нгуен, Патрик; Сайнат, Тара ; Кингсбери, Брайан (2012). «Глубокие нейронные сети для акустического моделирования в распознавании речи». Журнал обработки сигналов IEEE . 29 (6): 82–97. дои : 10.1109/MSP.2012.2205597 . S2CID 206485943 .

[4] Крижевский, Алекс; Суцкевер, Илья; Хинтон, Джеффри Э. (24 мая 2017 г.). «Классификация ImageNet с глубокими сверточными нейронными сетями» . Коммуникации АКМ . 60 (6): 84–90. дои : 10.1145/3065386 . ISSN 0001-0782 .

[5] Университет короля Абдель Азиза; Аль-Джохания, Нора; Эльрефаи, Ламияа; Университет Бенха (30 июня 2019 г.). «Распознавание дорсальной вен руки с помощью сверточных нейронных сетей: подходы к обучению функциям и переносу обучения» (PDF) . Международный журнал интеллектуальной инженерии и систем . 12 (3): 178–191. дои : 10.22266/ijies2019.0630.19 .

[6] Цыбенко, Г. (декабрь 1989 г.). «Приближение суперпозициями сигмоидальной функции» (PDF) . Математика управления, сигналов и систем . 2 (4): 303–314. дои : 10.1007/BF02551274 . ISSN 0932-4194 . S2CID 3958369 .

[7] Снейман, Январь (3 марта 2005 г.). Практическая математическая оптимизация: введение в базовую теорию оптимизации, а также классические и новые градиентные алгоритмы . Springer Science & Business Media. ISBN 978-0-387-24348-1 .

[8] Крижевский, Алекс; Суцкевер, Илья; Хинтон, Джеффри Э. (24 мая 2017 г.). «Классификация ImageNet с глубокими сверточными нейронными сетями» . Коммуникации АКМ . 60 (6): 84–90. дои : 10.1145/3065386 . ISSN 0001-0782 . S2CID 195908774 .

[9] Ходжкин, Алабама; Хаксли, А. Ф. (28 августа 1952 г.). «Количественное описание мембранного тока и его применение к проводимости и возбуждению нерва» . Журнал физиологии . 117 (4): 500–544. doi : 10.1113/jphysicalol.1952.sp004764 . ПМК 1392413 . ПМИД 12991237 .

[10] Наир, Винод; Хинтон, Джеффри Э. (2010), «Выпрямленные линейные единицы улучшают ограниченные машины Больцмана» , 27-я Международная конференция по машинному обучению , ICML'10, США: Omnipress, стр. 807–814, ISBN 9781605589077

[11] Глорот, Ксавье; Борд, Антуан; Бенджио, Йошуа (2011). «Глубокие разреженные нейронные сети выпрямителя» (PDF) . Международная конференция по искусственному интеллекту и статистике .

[12] Клеверт, Джорк-Арне; Унтертинер, Томас; Хохрайтер, Зепп (23 ноября 2015 г.). «Быстрое и точное глубокое сетевое обучение с помощью экспоненциальных линейных единиц (ELU)». arXiv : 1511.07289 [ cs.LG ].

[13] Кламбауэр, Гюнтер; Унтертинер, Томас; Майр, Андреас; Хохрайтер, Зепп (08.06.2017). «Самонормализующиеся нейронные сети». Достижения в области нейронных систем обработки информации . 30 (2017). arXiv : 1706.02515 .

[14] Маас, Эндрю Л.; Ханнун, Ауни Ю.; Нг, Эндрю Ю. (июнь 2013 г.). «Нелинейность выпрямителя улучшает акустические модели нейронных сетей». Учеб. ИКМЛ . 30 (1). S2CID 16489696 .

[15] Каймин; Чжан, Сянюй; Рен, Шаоцин; Сунь, Цзянь (06 г. Хэ , февраля . 2015 )

[refssbs1-16] Атто, Абдуррахман М.; Пастор Доминик; Мерсье, Грегуар (2008), «Плавное сжатие сигмовидного вейвлета для непараметрической оценки» (PDF) , Международная конференция IEEE по акустике, речи и обработке сигналов , 2008 г., стр. 3265–3268, doi : 10.1109/ICASSP.2008.4518347 , ISBN 978-1-4244-1483-3 , S2CID 9959057

[17] Эльфвинг, Стефан; Учибе, Эйдзи; Дойя, Кенджи (2018). «Сигмовидные линейные единицы для аппроксимации функций нейронной сети при обучении с подкреплением». Нейронные сети . 107 : 3–11. arXiv : 1702.03118 . дои : 10.1016/j.neunet.2017.12.012 . ПМИД 29395652 . S2CID 6940861 .

[18] Рамачандран, Праджит; Зоф, Баррет; Ле, Куок V (2017). «Поиск функций активации». arXiv : 1710.05941 [ cs.NE ].

[19] Гудфеллоу, Ян Дж.; Вард-Фарли, Дэвид; Мирза, Мехди; Курвиль, Аарон; Бенджио, Йошуа (2013). «Максаут Нетворкс». Материалы семинара и конференции JMLR . 28 (3): 1319–1327. arXiv : 1302.4389 .

[20] Маронезе, Марко; Дестри, Клаудио; Прати, Энрико (2022). «Квантовые функции активации для квантовых нейронных сетей». Квантовая обработка информации . 21 (4): 128. arXiv : 2201.03700 . Бибкод : 2022QuIP...21..128M . дои : 10.1007/s11128-022-03466-0 . ISSN 1570-0755 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]