Soboleva modified hyperbolic tangent
, Модифицированный гиперболический тангенс Соболевой также известный как (параметрическая) функция активации гиперболического тангенса, модифицированная Соболевой ([P]SMHTAF), [номер 1] — это специальная S-образная функция , основанная на гиперболическом тангенсе , определяемая формулой
| Уравнение | Управление левым хвостом | Управление правым хвостом |
|---|---|---|
 |  |
История
[ редактировать ]Первоначально эта функция была предложена как «модифицированный гиперболический тангенс». [номер 1] украинского моделирования ученого Елены В. Соболевой ( Елена В. Соболева ) как функция полезности для многокритериальной оптимизации и выбора при принятии решений . [1] [2] [3]
Практическое использование
[ редактировать ]С тех пор эта функция была введена в нейронных сетей . теорию и практику [4]
Он также использовался в экономике для моделирования потребления и инвестиций. [5] аппроксимировать вольт-амперные характеристики полевых транзисторов и светодиодов , [6] спроектировать антенные фидеры , [7] [ хищный издатель ] и анализировать температуру и плотность плазмы в диверторной зоне термоядерных реакторов . [8]
Чувствительность к параметрам
[ редактировать ]Производная функции определяется по формуле:
Следующие условия ограничивают функцию по осям y : a ≤ c , b ≤ d .
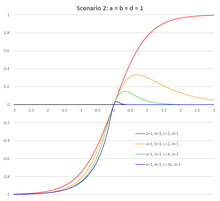
Было исследовано семейство рекуррентно-генерируемых параметрических гиперболических касательных функций активации Соболевой (NPSMHTAF, FPSMHTAF) с параметрами a = c и b = d . [9] Стоит отметить, что в этом случае функция не чувствительна к переворачиванию левого и правого параметров:
| Уравнение | Левая распространенность | Правое преобладание |
|---|---|---|
 |  |
Функция чувствительна к отношению коэффициентов знаменателя и часто используется без коэффициентов в числителе:
| Уравнение | Базовая диаграмма | Масштабированная функция |
|---|---|---|
Оцените конец: |  |  |
При параметрах a = b = c = d = 1 модифицированная гиперболическая функция тангенса сводится к обычной функции tanh ( x ), тогда как при a = b = 1 и c = d = 0 член становится равным sinh ( x ).
См. также
[ редактировать ]- Функция активации
- е (математическая константа)
- Теорема о равенстве вписанных окружностей , основанная на sinh
- Расстояние Хаусдорфа
- Обратные гиперболические функции
- Список интегралов от гиперболических функций
- Спирали Пуансо
- Сигмовидная функция
Примечания
[ редактировать ]- ^ Перейти обратно: а б Соболева предложила название «модифицированный гиперболический тангенс» (mtanh, mth), но поскольку другие авторы использовали это название и для других функций, некоторые авторы стали называть эту функцию «модифицированным гиперболическим тангенсом Соболевой».
Ссылки
[ редактировать ]- ^ Соболева Елена Владимировна; Бескоровайный, Владимир Валентинович (2008). Функция полезности в задачах структурной оптимизации распределенных объектов Функция для оценки полезности альтернатив в задачах структурной оптимизации территориально распределенных объектов . Четвертая научная конференция Харьковского университета Воздушных Сил имени Ивана Кожедуба, 16–17 апреля 2008 года (in Ukrainian). Kharkiv, Украина: Kharkiv University of Air Force (ХУПС/ХУПС). p. 121.
- ^ Soboleva, Elena Vladimirovna (2009). S-образная функция полезности част-ных критериев для многофакторной оценки проектных решений [ The S-shaped utility function of individual criteria for multi-objective decision-making in design ]. Материалы XIII Международного молодежного форума «Радиоэлектро-ника и молодежь в XXI веке» (Materials of the 13th international youth forum "Radioelectronics and youth in the 21st century") (in Russian). Kharkiv, Ukraine: Kharkiv National University of Radioelectronics (KNURE/ХНУРЕ). p. 247.
- ^ Beskorovainyi, Vladimir Valentinovich; Soboleva, Elena Vladimirovna (2010). ИДЕНТИФИКАЦИЯ ЧАСТНОй ПОлЕЗНОСТИ МНОГОФАКТОРНЫХ АлЬТЕРНАТИВ С ПОМОЩЬЮ S-ОБРАЗНЫХ ФУНКЦИй [Идентификация функций полезности при моделировании многоцелевого выбора с использованием S-образных функций] (PDF) . Проблемы бионики: Республиканский Межведомственный Научно-Технический Сборник БИОНИКА ИНТЕЛЛЕКТА [ Бионика интеллекта ] (на русском языке). Том. 72, нет. 1. Харьковский национальный университет радиоэлектроники (ХНУРЭ/ХНУРЕ). стр. 50–54. ISSN 0555-2656 . УДК 519.688:004.896. Архивировано (PDF) из оригинала 21 июня 2022 г. Проверено 19 июня 2020 г. (5 страниц) [1]
- ^ Малинова, Анна; Голев, Ангел; Илиев, Антон; Кюркчиев, Николай (август 2017 г.). «Семейство повторяющихся функций активации, основанных на функции Гудермана» (PDF) . Международный журнал инженерных исследований и исследований в области управления . 4 (8). Факультет математики и информатики Пловдивского университета имени Паисия Хилендарского, Пловдив, Болгария: 38–48. ISSN 2394-7659 . Архивировано (PDF) из оригинала 14 июля 2022 г. Проверено 19 июня 2020 г. (11 страниц) [2]
- ^ Орландо, Джузеппе (01 июля 2016 г.). «Дискретная математическая модель хаотической динамики в экономике: модель Калдора делового цикла» . Математика и компьютеры в моделировании . 8-й семинар СТРУКТУРНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ: Вычислительные аспекты; Под редакцией Николетты Дель Буоно, Роберто Гарраппы и Джулии Спалетты и «Нестандартные приложения компьютерной алгебры» (ACA'2013); Под редакцией Франсиско Ботаны, Антонио Эрнандо, Эухенио Роанеса-Лозано и Майкла Дж. Вестера. 125 : 83–98. дои : 10.1016/j.matcom.2016.01.001 . ISSN 0378-4754 .
- ^ Tuev, Vasily I.; Uzhanin, Maxim V. (2009). ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОЙ ФУНКЦИИ ГИПЕРБОЛИЧЕСКОГО ТАНГЕНСА ДЛЯ АППРОКСИМАЦИИ ВОЛЬТАМПЕРНЫХ ХАРАКТЕРИСТИК ПОЛЕВЫХ ТРАНЗИСТОРОВ [ Использование модифицированной функции гиперболического тангенса для аппроксимации вольт-амперных характеристик полевых транзисторов ] (на русском языке). Томск, Россия: Томский политехнический университет (ТПУ/ТПУ). стр. 135–138. № 4/314. Архивировано из оригинала 15 августа 2017 г. Проверено 5 ноября 2015 г. (4 страницы) [3]
- ^ Голев, Ангел; Джамийков, Тодор; Кюркчиев, Николай (23 ноября 2017 г.) [09 октября 2017 г., 19 августа 2017 г.]. «Сигмоидальные функции в антенно-фидерной технике» (PDF) . Международный журнал чистой и прикладной математики . 116 (4). Факультет математики и информатики, Пловдивский университет «Паисий Хилендарский», Пловдив, Болгария / Софийский технический университет , София, Болгария: Академические публикации, ООО: 1081–1092. doi : 10.12732/ijpam.v116i4.23 (неактивен 31 января 2024 г.). ISSN 1311-8080 . Архивировано (PDF) из оригинала 19 июня 2020 г. Проверено 19 июня 2020 г.
{{cite journal}}: CS1 maint: DOI неактивен по состоянию на январь 2024 г. ( ссылка ) (12 страниц) - ^ Рубино, Джулио (15 января 2018 г.) [14 января 2018 г.]. Анализ данных о выхлопных газах и моделирование усовершенствованной конфигурации дивертора (Диссертация). Докторская степень по совместным исследованиям в области термоядерной науки и техники XXX (на английском, итальянском и португальском языках). Падуя, Италия: Центр термоядерных исследований (CRF), Падуанский университет / Неаполитанский университет Федерико II / Высший технический институт (IST), Университет Лиссабона . п. 84. ID 10811. Архивировано из оригинала 19 июня 2020 г. Проверено 19 июня 2020 г.
{{cite book}}: CS1 maint: bot: статус исходного URL неизвестен ( ссылка ) (2+viii+3*iii+102 страницы) - ^ Голев, Ангел; Илиев, Антон; Кюркчиев, Николай (июнь 2017 г.). «Заметка о модифицированной функции активации гиперболического тангенса Соболевой» (PDF) . Международный журнал инновационной науки, техники и технологий (JISET) . 4 (6). Факультет математики и информатики Пловдивского университета имени Паисия Хилендарского, Пловдив, Болгария: 177–182. ISSN 2348-7968 . Архивировано (PDF) из оригинала 19 июня 2020 г. Проверено 19 июня 2020 г. (6 страниц) [4]
Дальнейшее чтение
[ редактировать ]- Илиев, Антон; Кюркчиев Николай; Марков, Святослав (2017). «Заметка о новой функции активации типа Гомпертца» . Биоматические коммуникации . 4 (2). Факультет математики и информатики Пловдивского университета имени Паисия Хилендарского, Пловдив, Болгария / Институт математики и информатики Болгарской академии наук , София, Болгария: Форум биоматематиков (BF). дои : 10.11145/10.11145/bmc.2017.10.201 . ISSN 2367-5233 . Архивировано из оригинала 20 июня 2020 г. Проверено 19 июня 2020 г. (20 страниц) [5]





