Авторегрессионная модель

В статистике, эконометрике и обработке сигналов авторегрессионная ( AR ) модель представляет собой представление типа случайного процесса; как таковая, она используется для описания определенных изменяющихся во времени процессов в природе, экономике, поведении и т. д. Модель авторегрессии определяет, что выходная переменная линейно зависит от ее собственных предыдущих значений и от стохастического члена (несовершенно предсказуемого термина); таким образом, модель имеет форму стохастического разностного уравнения (или рекуррентного соотношения), которое не следует путать с дифференциальным уравнением . Вместе с моделью скользящего среднего (MA) это частный случай и ключевой компонент более общих моделей временных рядов авторегрессии – скользящего среднего (ARMA) и авторегрессионного интегрированного скользящего среднего (ARIMA), которые имеют более сложную стохастические модели. состав; это также частный случай векторной авторегрессионной модели (VAR), которая состоит из системы более чем одного взаимосвязанного стохастического разностного уравнения с более чем одной развивающейся случайной величиной.

В отличие от модели скользящего среднего (MA), авторегрессионная модель не всегда стационарна, поскольку может содержать единичный корень.

Хотя модели большого языка называются авторегрессионными, они не являются классической моделью авторегрессии в этом смысле, поскольку они не линейны.

Определение

Обозначения $AR(p)$указывает на авторегрессионную модель порядка p . Модель AR( p ) определяется как

$X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}$

где $\varphi _{1},\ldots ,\varphi _{p}$ – параметры модели , а $\varepsilon _{t}$ это белый шум . Это можно эквивалентно записать с использованием оператора обратного сдвига B как

$X_{t}=\sum _{i=1}^{p}\varphi _{i}B^{i}X_{t}+\varepsilon _{t}$

так что, перемещая член суммирования в левую часть и используя полиномиальную запись , мы имеем

$\phi [B]X_{t}=\varepsilon _{t}$

Таким образом, авторегрессионную модель можно рассматривать как выходной сигнал всеполюсного фильтра с бесконечной импульсной характеристикой , входным сигналом которого является белый шум.

Некоторые ограничения параметров необходимы для того, чтобы модель оставалась стационарной в слабом смысле . Например, процессы в модели AR(1) с $|\varphi _{1}|\geq 1$не являются стационарными. В более общем смысле, чтобы модель AR( p ) была стационарной в слабом смысле, корни полинома $\Phi (z):=\textstyle 1-\sum _{i=1}^{p}\varphi _{i}z^{i}$ должен лежать вне единичного круга , т. е. каждый (комплексный) корень $z_{i}$ должен удовлетворить $|z_{i}|>1$ (см. стр. 89,92 ).

шоков

В процессе AR однократный шок влияет на значения развивающейся переменной бесконечно далеко в будущее. Например, рассмотрим модель AR(1) $X_{t}=\varphi _{1}X_{t-1}+\varepsilon _{t}$. Ненулевое значение для $\varepsilon _{t}$ в момент времени t =1 влияет $X_{1}$ по сумме $\varepsilon _{1}$. Тогда по уравнению АР для $X_{2}$ с точки зрения $X_{1}$, это влияет $X_{2}$ по сумме $\varphi _{1}\varepsilon _{1}$. Тогда по уравнению АР для $X_{3}$ с точки зрения $X_{2}$, это влияет $X_{3}$ по сумме $\varphi _{1}^{2}\varepsilon _{1}$. Продолжение этого процесса показывает, что эффект $\varepsilon _{1}$ никогда не заканчивается, хотя если процесс стационарен , то в пределе эффект уменьшается до нуля.

Поскольку каждый шок влияет на значения X бесконечно далеко в будущем от момента их возникновения, на любое заданное значение X _t влияют потрясения, происходящие бесконечно далеко в прошлом. В этом также можно убедиться, переписав авторегрессию

$\phi (B)X_{t}=\varepsilon _{t}\,$

(где постоянный член был исключен, предполагая, что переменная измерялась как отклонения от ее среднего значения) как

$X_{t}={\frac {1}{\phi (B)}}\varepsilon _{t}\,.$

Когда полиномиальное деление в правой части, полином в операторе обратного сдвига применяется к выполняется $\varepsilon _{t}$ имеет бесконечный порядок, то есть бесконечное число запаздывающих значений $\varepsilon _{t}$ появляются в правой части уравнения.

Характеристический полином

Автокорреляционную функцию процесса AR( p ) можно выразить как

$\rho (\tau )=\sum _{k=1}^{p}a_{k}y_{k}^{-|\tau |},$

где $y_{k}$ являются корнями многочлена

$\phi (B)=1-\sum _{k=1}^{p}\varphi _{k}B^{k}$

где B — оператор обратного сдвига , где $\phi (\cdot )$ — функция, определяющая авторегрессию, и где $\varphi _{k}$– коэффициенты авторегрессии. Формула справедлива только в том случае, если все корни имеют кратность 1.

Автокорреляционная функция процесса AR( p ) представляет собой сумму затухающих экспонент.

• Каждый действительный корень вносит в автокорреляционную функцию компонент, который затухает экспоненциально.
• Точно так же каждая пара комплексно-сопряженных корней вносит экспоненциально затухающее колебание.

Графики процессов AR( p )

АР(0); AR(1) с параметром AR 0,3; AR(1) с параметром AR 0,9; AR(2) с параметрами AR 0,3 и 0,3; и AR(2) с параметрами AR 0,9 и -0,8.

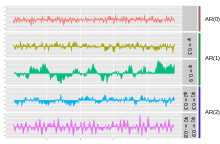
Простейшим процессом AR является AR(0), который не имеет зависимости между членами. На результат процесса влияет только фактор ошибки/инновации/шума, поэтому на рисунке AR(0) соответствует белому шуму.

Для процесса AR(1) с положительным $\varphi$, только предыдущий член процесса и шумовой член вносят вклад в выходной сигнал. Если $\varphi$ близко к 0, то процесс по-прежнему выглядит как белый шум, но поскольку $\varphi$приближается к 1, выход получает больший вклад от предыдущего члена относительно шума. Это приводит к «сглаживанию» или интеграции выходного сигнала, подобно фильтру нижних частот .

Для процесса AR(2) два предыдущих члена и шумовой член вносят вклад в выходные данные. Если оба $\varphi _{1}$ и $\varphi _{2}$положительны, выходной сигнал будет напоминать фильтр нижних частот с уменьшением высокочастотной части шума. Если $\varphi _{1}$ является положительным, пока $\varphi _{2}$отрицательно, то процесс благоприятствует изменению знака между членами процесса. Выходной сигнал колеблется. Это можно сравнить с обнаружением края или обнаружением изменения направления.

Пример: процесс AR(1)

Процесс AR(1) определяется следующим образом:

$$X_{t}=\varphi X_{t-1}+\varepsilon _{t}\,$$

где $\varepsilon _{t}$ представляет собой процесс белого шума с нулевым средним значением и постоянной дисперсией $\sigma _{\varepsilon }^{2}$. (Примечание: нижний индекс на $\varphi _{1}$ был отброшен.) Процесс является стационарным в слабом смысле , если $|\varphi |<1$поскольку он получается как выходной сигнал стабильного фильтра, входным сигналом которого является белый шум. (Если $\varphi =1$ тогда дисперсия $X_{t}$ зависит от временной задержки t, так что дисперсия ряда расходится к бесконечности при стремлении t к бесконечности и, следовательно, не является стационарной в слабом смысле.) $|\varphi |<1$, Значение $\operatorname {E} (X_{t})$одинаково для всех значений t по самому определению слабой смысловой стационарности. Если среднее значение обозначается $\mu$, это следует из

$$\operatorname {E} (X_{t})=\varphi \operatorname {E} (X_{t-1})+\operatorname {E} (\varepsilon _{t}),$$

что

$$\mu =\varphi \mu +0,$$

и поэтому

$\mu =0.$

Дисперсия ​ ​

${\textrm {var}}(X_{t})=\operatorname {E} (X_{t}^{2})-\mu ^{2}={\frac {\sigma _{\varepsilon }^{2}}{1-\varphi ^{2}}},$

где $\sigma _{\varepsilon }$ стандартное отклонение $\varepsilon _{t}$. Это можно показать, заметив, что

${\textrm {var}}(X_{t})=\varphi ^{2}{\textrm {var}}(X_{t-1})+\sigma _{\varepsilon }^{2},$

а затем заметив, что указанная выше величина является стабильной фиксированной точкой этого отношения.

Автоковариация выражением определяется

$B_{n}=\operatorname {E} (X_{t+n}X_{t})-\mu ^{2}={\frac {\sigma _{\varepsilon }^{2}}{1-\varphi ^{2}}}\,\,\varphi ^{|n|}.$

Видно, что автоковариационная функция затухает со временем затухания (также называемым постоянной времени ) $\tau =1-\varphi$.

преобразование Фурье Функция спектральной плотности представляет собой функции автоковариации. В дискретных терминах это будет преобразование Фурье с дискретным временем:

$\Phi (\omega )={\frac {1}{\sqrt {2\pi }}}\,\sum _{n=-\infty }^{\infty }B_{n}e^{-i\omega n}={\frac {1}{\sqrt {2\pi }}}\,\left({\frac {\sigma _{\varepsilon }^{2}}{1+\varphi ^{2}-2\varphi \cos(\omega )}}\right).$

Это выражение является периодическим из-за дискретного характера $X_{j}$, что проявляется в виде косинуса в знаменателе. Если предположить, что время выборки ( $\Delta t=1$) намного меньше времени затухания ( $\tau$), то мы можем использовать континуальное приближение для $B_{n}$:

$B(t)\approx {\frac {\sigma _{\varepsilon }^{2}}{1-\varphi ^{2}}}\,\,\varphi ^{|t|}$

что дает лоренцев профиль спектральной плотности:

$\Phi (\omega )={\frac {1}{\sqrt {2\pi }}}\,{\frac {\sigma _{\varepsilon }^{2}}{1-\varphi ^{2}}}\,{\frac {\gamma }{\pi (\gamma ^{2}+\omega ^{2})}}$

где $\gamma =1/\tau$ - угловая частота, связанная со временем затухания $\tau$.

Альтернативное выражение для $X_{t}$ можно получить, предварительно подставив $\varphi X_{t-2}+\varepsilon _{t-1}$ для $X_{t-1}$в определяющем уравнении. Продолжение этого процесса N раз дает

$X_{t}=\varphi ^{N}X_{t-N}+\sum _{k=0}^{N-1}\varphi ^{k}\varepsilon _{t-k}.$

Для N, стремящегося к бесконечности, $\varphi ^{N}$ будет приближаться к нулю и:

$X_{t}=\sum _{k=0}^{\infty }\varphi ^{k}\varepsilon _{t-k}.$

Видно, что $X_{t}$ белый шум свернут с $\varphi ^{k}$ядро плюс постоянное среднее значение. Если белый шум $\varepsilon _{t}$ это гауссов процесс тогда $X_{t}$также является гауссовским процессом. В других случаях центральная предельная теорема указывает, что $X_{t}$ будет примерно нормально распределено, когда $\varphi$ близко к единице.

Для $\varepsilon _{t}=0$, процесс $X_{t}=\varphi X_{t-1}$будет геометрическая прогрессия ( экспоненциальный рост или затухание). В этом случае решение можно найти аналитически: $X_{t}=a\varphi ^{t}$ Посредством чего $a$ — неизвестная константа ( начальное условие ).

/разности процесса AR(1

Модель AR(1) представляет собой аналог непрерывного процесса Орнштейна-Уленбека в дискретном времени . Поэтому иногда полезно понять свойства модели AR(1), представленной в эквивалентной форме. В этой форме модель AR(1) с параметром процесса $\theta \in \mathbb {R}$, дан кем-то

$X_{t+1}=X_{t}+(1-\theta )(\mu -X_{t})+\varepsilon _{t+1}$, где $|\theta |<1\,$, $\mu :=E(X)$ является средним значением модели, и $\{\epsilon _{t}\}$ представляет собой процесс белого шума с нулевым средним значением и постоянной дисперсией $\sigma$.

Переписав это как $X_{t+1}=\theta X_{t}+(1-\theta )\mu +\varepsilon _{t+1}$ и затем выводим (по индукции) $X_{t+n}=\theta ^{n}X_{t}+(1-\theta ^{n})\mu +\Sigma _{i=1}^{n}\left(\theta ^{n-i}\epsilon _{t+i}\right)$, можно показать, что

$\operatorname {E} (X_{t+n}|X_{t})=\mu \left[1-\theta ^{n}\right]+X_{t}\theta ^{n}$ и

$\operatorname {Var} (X_{t+n}|X_{t})=\sigma ^{2}{\frac {1-\theta ^{2n}}{1-\theta ^{2}}}$.

Выбор максимального лага

Основная статья: Частичная автокорреляционная функция

Частичная автокорреляция процесса AR(p) равна нулю при задержках, превышающих p, поэтому подходящим максимальным лагом p является тот, после которого все частичные автокорреляции равны нулю.

Расчет параметров АР

Существует много способов оценки коэффициентов, например, обычная процедура наименьших квадратов или метод моментов (с помощью уравнений Юла – Уокера).

Модель AR( p ) задается уравнением

$X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}.\,$

Он основан на параметрах $\varphi _{i}$где я = 1, ..., п . Существует прямое соответствие между этими параметрами и ковариационной функцией процесса, и это соответствие можно инвертировать для определения параметров из автокорреляционной функции (которая сама получается из ковариаций). Это делается с помощью уравнений Юла – Уокера.

–

Уравнения Юла-Уокера, названные в честь Удного Юла и Гилберта Уокера , представляют собой следующую систему уравнений.

$\gamma _{m}=\sum _{k=1}^{p}\varphi _{k}\gamma _{m-k}+\sigma _{\varepsilon }^{2}\delta _{m,0},$

где m = 0,…, p , что дает p + 1 уравнений. Здесь $\gamma _{m}$ — автоковариационная функция X _t , $\sigma _{\varepsilon }$ - стандартное отклонение входного шумового процесса, а $\delta _{m,0}$ – дельта - функция Кронекера .

Поскольку последняя часть отдельного уравнения отлична от нуля только в том случае, если m = 0 , набор уравнений можно решить, представив уравнения для m > 0 в матричной форме, получив таким образом уравнение

${\begin{bmatrix}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\\\vdots \\\gamma _{p}\\\end{bmatrix}}={\begin{bmatrix}\gamma _{0}&\gamma _{-1}&\gamma _{-2}&\cdots \\\gamma _{1}&\gamma _{0}&\gamma _{-1}&\cdots \\\gamma _{2}&\gamma _{1}&\gamma _{0}&\cdots \\\vdots &\vdots &\vdots &\ddots \\\gamma _{p-1}&\gamma _{p-2}&\gamma _{p-3}&\cdots \\\end{bmatrix}}{\begin{bmatrix}\varphi _{1}\\\varphi _{2}\\\varphi _{3}\\\vdots \\\varphi _{p}\\\end{bmatrix}}$

который можно решить для всех $\{\varphi _{m};m=1,2,\dots ,p\}.$ Оставшееся уравнение для m = 0 имеет вид

$\gamma _{0}=\sum _{k=1}^{p}\varphi _{k}\gamma _{-k}+\sigma _{\varepsilon }^{2},$

который однажды $\{\varphi _{m};m=1,2,\dots ,p\}$ известны, могут быть решены для $\sigma _{\varepsilon }^{2}.$

Альтернативная формулировка заключается в использовании автокорреляционной функции . Параметры АР определяются первыми p +1 элементами $\rho (\tau )$автокорреляционной функции. Полную автокорреляционную функцию затем можно получить путем рекурсивного вычисления

$\rho (\tau )=\sum _{k=1}^{p}\varphi _{k}\rho (k-\tau )$

низкого порядка Примеры некоторых процессов AR( p )

• р =1
  • $\gamma _{1}=\varphi _{1}\gamma _{0}$
  • Следовательно $\rho _{1}=\gamma _{1}/\gamma _{0}=\varphi _{1}$
• р =2
  • Уравнения Юла – Уокера для процесса AR (2) имеют вид

    $\gamma _{1}=\varphi _{1}\gamma _{0}+\varphi _{2}\gamma _{-1}$

    $\gamma _{2}=\varphi _{1}\gamma _{1}+\varphi _{2}\gamma _{0}$

    • Помните, что $\gamma _{-k}=\gamma _{k}$
    • Использование первого уравнения дает $\rho _{1}=\gamma _{1}/\gamma _{0}={\frac {\varphi _{1}}{1-\varphi _{2}}}$
    • Использование формулы рекурсии дает $\rho _{2}=\gamma _{2}/\gamma _{0}={\frac {\varphi _{1}^{2}-\varphi _{2}^{2}+\varphi _{2}}{1-\varphi _{2}}}$

Оценка параметров AR

Приведенные выше уравнения (уравнения Юла-Уокера) обеспечивают несколько способов оценки параметров модели AR( p ) путем замены теоретических ковариаций оценочными значениями. Некоторые из этих вариантов можно описать следующим образом:

• Оценка автоковариаций или автокорреляций. Здесь каждый из этих членов оценивается отдельно, используя традиционные оценки. Существуют разные способы сделать это, и выбор между ними влияет на свойства схемы оценки. Например, некоторые варианты выбора могут дать отрицательные оценки дисперсии.
• Формулировка в виде задачи регрессии по методу наименьших квадратов, в которой строится обычная задача прогнозирования по методу наименьших квадратов, основанная на прогнозировании значений X _t на основе p предыдущих значений той же серии. Это можно рассматривать как схему прогнозирования. Можно увидеть, что нормальные уравнения для этой задачи соответствуют аппроксимации матричной формы уравнений Юла – Уокера, в которой каждое появление автоковариации с одним и тем же запаздыванием заменяется несколько другой оценкой.
• Формулировка как расширенная форма обычной задачи прогнозирования методом наименьших квадратов. Здесь два набора уравнений прогнозирования объединяются в одну схему оценки и один набор нормальных уравнений. Один набор представляет собой набор уравнений прямого прогнозирования, а другой — соответствующий набор уравнений обратного прогнозирования, относящихся к обратному представлению модели AR:

$X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t+i}+\varepsilon _{t}^{*}\,.$

Здесь прогнозируемые значения X _t будут основаны на будущих значениях p того же ряда. Этот способ оценки параметров AR принадлежит Джону Паркеру Бургу, и называется методом Бурга: Бург и более поздние авторы назвали эти конкретные оценки «оценками максимальной энтропии». но причина этого применима к использованию любого набора оцененных параметров AR. По сравнению со схемой оценки, использующей только уравнения прямого прогнозирования, получаются разные оценки автоковариаций, и эти оценки имеют разные свойства устойчивости. Оценки Бурга особенно связаны с оценкой спектра максимальной энтропии .

Другие возможные подходы к оценке включают оценку максимального правдоподобия . Доступны два различных варианта максимального правдоподобия: в одном (в широком смысле эквивалентном схеме наименьших квадратов прямого прогнозирования) рассматриваемая функция правдоподобия соответствует условному распределению более поздних значений в серии с учетом начальных значений p в серии; во втором случае рассматривается функция правдоподобия, соответствующая безусловному совместному распределению всех значений в наблюдаемом ряду. Существенные различия в результатах этих подходов могут возникнуть, если наблюдаемый ряд короткий или процесс близок к нестационарности.

Спектр

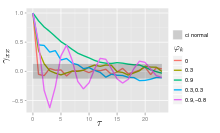
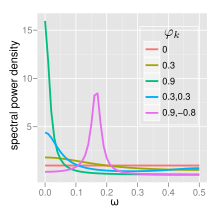
( Спектральная плотность мощности PSD) процесса AR( p ) с дисперсией шума $\mathrm {Var} (Z_{t})=\sigma _{Z}^{2}$ является

$S(f)={\frac {\sigma _{Z}^{2}}{|1-\sum _{k=1}^{p}\varphi _{k}e^{-i2\pi fk}|^{2}}}.$

АР(0)

Для белого шума (AR(0))

$S(f)=\sigma _{Z}^{2}.$

АР(1)

Для АР(1)

$S(f)={\frac {\sigma _{Z}^{2}}{|1-\varphi _{1}e^{-2\pi if}|^{2}}}={\frac {\sigma _{Z}^{2}}{1+\varphi _{1}^{2}-2\varphi _{1}\cos 2\pi f}}$

• Если $\varphi _{1}>0$имеется единственный спектральный пик при f=0, часто называемый красным шумом . Как $\varphi _{1}$становится ближе к 1, мощность на низких частотах увеличивается, т. е. увеличиваются временные задержки. Это фильтр нижних частот: при применении к свету полного спектра все, кроме красного света, будет фильтроваться.
• Если $\varphi _{1}<0$существует минимум при f=0, часто называемый синим шумом . Это аналогично действует как фильтр верхних частот: все, кроме синего света, будет фильтроваться.

АР(2)

Поведение процесса AR(2) полностью определяется корнями его характеристического уравнения , которое выражается через оператор запаздывания как:

$1-\varphi _{1}B-\varphi _{2}B^{2}=0,$

или, что эквивалентно, полюсами его передаточной функции , которая определяется в области Z следующим образом:

$H_{z}=(1-\varphi _{1}z^{-1}-\varphi _{2}z^{-2})^{-1}.$

Отсюда следует, что полюса представляют собой значения z, удовлетворяющие:

$1-\varphi _{1}z^{-1}-\varphi _{2}z^{-2}=0$,

который дает:

$z_{1},z_{2}={\frac {1}{2\varphi _{2}}}\left(\varphi _{1}\pm {\sqrt {\varphi _{1}^{2}+4\varphi _{2}}}\right)$.

$z_{1}$ и $z_{2}$ являются обратными характеристическим корням, а также собственными значениями матрицы временного обновления:

${\begin{bmatrix}\varphi _{1}&\varphi _{2}\\1&0\end{bmatrix}}$

Процессы AR(2) можно разделить на три группы в зависимости от характеристик их корней/полюсов:

• Когда $\varphi _{1}^{2}+4\varphi _{2}<0$, процесс имеет пару комплексно-сопряженных полюсов, создающих среднечастотный пик на:

$f^{*}={\frac {1}{2\pi }}\cos ^{-1}\left({\frac {\varphi _{1}}{2{\sqrt {-\varphi _{2}}}}}\right),$

с шириной полосы около пика, обратно пропорциональной модулям полюсов:

$|z_{1}|=|z_{2}|={\sqrt {-\varphi _{2}}}.$

Все члены, содержащие квадратные корни, действительны в случае комплексных полюсов, поскольку они существуют только тогда, когда $\varphi _{2}<0$.

В противном случае процесс имеет реальные корни, и:

• Когда $\varphi _{1}>0$ он действует как фильтр нижних частот белого шума со спектральным пиком на уровне $f=0$
• Когда $\varphi _{1}<0$ он действует как фильтр верхних частот белого шума со спектральным пиком на уровне $f=1/2$.

Процесс является нестационарным, когда полюса находятся на единичной окружности или за ее пределами, или, что то же самое, когда характеристические корни находятся на единичной окружности или внутри нее. Процесс устойчив, когда полюса находятся строго внутри единичного круга (корни строго вне единичного круга) или, что то же самое, когда коэффициенты находятся в треугольнике. $-1\leq \varphi _{2}\leq 1-|\varphi _{1}|$.

Полную функцию PSD можно выразить в реальной форме как:

$S(f)={\frac {\sigma _{Z}^{2}}{1+\varphi _{1}^{2}+\varphi _{2}^{2}-2\varphi _{1}(1-\varphi _{2})\cos(2\pi f)-2\varphi _{2}\cos(4\pi f)}}$

Реализации в пакетах статистики

• R , пакет статистики включает функцию ar .
• R, пакет astsa включает функцию sarima , подходящую для различных моделей, включая модели AR.
• MATLAB Набор инструментов эконометрики и панель инструментов идентификации системы включает авторегрессионные модели
• Matlab и Octave : набор инструментов TSA содержит несколько функций оценки для одномерных, многомерных и адаптивных авторегрессионных моделей.
• PyMC3 : среда байесовской статистики и вероятностного программирования поддерживает режимы авторегрессии с задержками .
• bayesloop поддерживает вывод параметров и выбор модели для процесса AR-1 с изменяющимися во времени параметрами.
• Python : реализация в моделях состояний.

Импульсный отклик

Импульсная реакция системы — это изменение развивающейся переменной в ответ на изменение значения шокового члена k периодов ранее в зависимости от k . Поскольку модель AR является частным случаем векторной авторегрессионной модели, здесь применяется вычисление импульсного отклика в векторной авторегрессии#импульсный отклик .

n -прогнозирование на шаг вперед

Как только параметры авторегрессии

$X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}\,$

были оценены, авторегрессию можно использовать для прогнозирования произвольного числа периодов в будущем. Сначала используйте t для обозначения первого периода, по которому данные еще недоступны; подставьте известные предыдущие значения X _t-i для i = 1, ..., p в уравнение авторегрессии, установив при этом член ошибки $\varepsilon _{t}$равно нулю (поскольку мы прогнозируем, что X _t будет равен его ожидаемому значению, а ожидаемое значение ненаблюдаемой ошибки равно нулю). Результатом уравнения авторегрессии является прогноз на первый ненаблюдаемый период. Затем используйте t для обозначения следующего периода, за который данные еще недоступны; снова для составления прогноза используется уравнение авторегрессии, с одним отличием: значение X за период до прогнозируемого сейчас неизвестно, поэтому вместо него используется его ожидаемое значение - прогнозируемое значение, возникающее на предыдущем этапе прогнозирования. . Затем для будущих периодов используется та же процедура, каждый раз с использованием еще одного прогнозного значения в правой части прогнозного уравнения до тех пор, пока после p прогнозов все p правых значений не станут прогнозными значениями из предыдущих шагов.

Существует четыре источника неопределенности в отношении прогнозов, полученных таким образом: (1) неопределенность относительно того, является ли модель авторегрессии правильной моделью; (2) неопределенность в отношении точности прогнозируемых значений, которые используются в качестве запаздывающих значений в правой части уравнения авторегрессии; (3) неопределенность относительно истинных значений коэффициентов авторегрессии; и (4) неопределенность относительно значения ошибки. $\varepsilon _{t}\,$на прогнозируемый период. Каждый из последних трех показателей можно оценить количественно и объединить, чтобы получить доверительный интервал для прогнозов на n шагов вперед; доверительный интервал станет шире по мере увеличения n из-за использования все большего числа оценочных значений для правых переменных.

См. также

• Модель скользящего среднего
• Линейное разностное уравнение
• Прогнозная аналитика
• Линейное прогнозирующее кодирование
• Резонанс
• Рекурсия Левинсона
• Процесс Орнштейна – Уленбека
• Бесконечная импульсная характеристика

Ссылки

• Миллс, Теренс К. (1990). Методы временных рядов для экономистов . Издательство Кембриджского университета. ISBN  9780521343398 .
• Персиваль, Дональд Б.; Уолден, Эндрю Т. (1993). Спектральный анализ для физических приложений . Издательство Кембриджского университета. Бибкод : 1993sapa.book.....P .
• Пандит, Судхакар М.; Ву, Шиен-Мин (1983). Временные ряды и системный анализ с приложениями . Джон Уайли и сыновья.

Внешние ссылки

• Авторегрессионный анализ (AR) Пола Бурка
• Лекция по эконометрике (тема: Модели авторегрессии) на YouTube Марка Тома