Случайное блуждание с максимальной энтропией

Случайное блуждание с максимальной энтропией ( MERW ) — популярный тип смещенного случайного блуждания по графу , в котором вероятности перехода выбираются в соответствии с принципом максимальной энтропии , который гласит, что распределение вероятностей , которое лучше всего представляет текущее состояние знаний, является тем, которое с наибольшей энтропией. В то время как стандартное случайное блуждание выбирает для каждой вершины равномерное распределение вероятностей среди ее исходящих ребер, локально максимизируя уровень энтропии , MERW максимизирует его глобально (среднее производство энтропии ), предполагая равномерное распределение вероятностей среди всех путей в данном графе.

MERW используется в различных областях науки. Прямое применение — это выбор вероятностей для максимизации скорости передачи через ограниченный канал, аналогично кодированию Фибоначчи . Его свойства также сделали его полезным, например, при анализе сложных сетей. например, прогнозирование ссылок , обнаружение сообщества, надежная транспортировка по сетям и меры центральности . Также при анализе изображений , например, для обнаружения областей визуальной значимости, локализация объекта, обнаружение взлома или проблема с трактографией .

Кроме того, он воссоздает некоторые свойства квантовой механики , предлагая способ исправить несоответствие между моделями диффузии и квантовыми предсказаниями, например, локализацию Андерсона .

Базовая модель

Слева: базовая концепция общего случайного блуждания (GRW) и случайного блуждания с максимальной энтропией (MERW).
Справа: пример их эволюции на одной и той же неоднородной двумерной решетке с циклическими граничными условиями – плотностью вероятности после 10, 100 и 1000 шагов при старте из одной вершины. Маленькие прямоугольники обозначают дефекты: все вершины, кроме отмеченных, имеют дополнительный петель (ребро к себе). Для правильных решеток (без дефектов) GRW и MERW идентичны. Хотя дефекты не сильно влияют на локальное поведение, они приводят здесь к совершенно иной глобальной стационарной вероятности. В то время как GRW (и основанная на нем стандартная диффузия ) приводит к почти однородной стационарной плотности, MERW обладает сильным свойством локализации, заключая ходоков в энтропийные ямы по аналогии с электронами в дефектной решетке полупроводника .

Рассмотрим график с $n$ вершины, определяемые матрицей смежности $A\in \left\{0,1\right\}^{n\times n}$: $A_{ij}=1$ если есть ребро из вершины $i$ к $j$, 0 в противном случае. Для простоты предположим, что это неориентированный граф , соответствующий симметричному $A$; однако MERW также можно обобщить для ориентированных и взвешенных графов (например, распределение Больцмана по путям вместо равномерного).

на этом графе мы хотели бы выбрать случайное блуждание В качестве марковского процесса : для каждой вершины $i$ и его исходящий край $j$, выберите вероятность $S_{ij}$ ходока, случайно воспользовавшегося этим краем после посещения $i$. Формально, найдите стохастическую матрицу $S$ (содержащий вероятности перехода цепи Маркова) такие, что

• $0\leq S_{ij}\leq A_{ij}$ для всех $i,j$ и
• $\sum _{j=1}^{n}S_{ij}=1$ для всех $i$.

Предполагая, что этот граф связен, а не периодичен , эргодическая теория утверждает, что эволюция этого случайного процесса приводит к некоторому стационарному распределению вероятностей. $\rho$ такой, что $\rho S=\rho$.

Используя энтропию Шеннона для каждой вершины и усредняя вероятность посещения этой вершины (чтобы иметь возможность использовать ее энтропию), мы получаем следующую формулу для среднего производства энтропии ( скорости энтропии ) случайного процесса:

$H(S)=\sum _{i=1}^{n}\rho _{i}\sum _{j=1}^{n}S_{ij}\log(1/S_{ij})$

Это определение оказывается эквивалентным асимптотической средней энтропии (на длину) распределения вероятностей в пространстве путей для этого случайного процесса.

В стандартном случайном блуждании, называемом здесь общим случайным блужданием (GRW), мы естественным образом выбираем, чтобы каждое исходящее ребро было равновероятным:

$S_{ij}={\frac {A_{ij}}{\sum \limits _{k=1}^{n}A_{ik}}}$.

Для симметричного $A$ это приводит к стационарному распределению вероятностей $\rho$ с

$\rho _{i}={\frac {\sum \limits _{j=1}^{n}A_{ij}}{\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}A_{ij}}}$.

Он локально максимизирует производство энтропии (неопределенность) для каждой вершины, но обычно приводит к неоптимальному среднему глобальному уровню энтропии. $H(S)$.

MERW выбирает стохастическую матрицу, которая максимизирует $H(S)$или, что то же самое, предполагает равномерное распределение вероятностей среди всех путей в данном графе. Его формула получается путем предварительного вычисления доминирующего собственного значения. $\lambda$ и соответствующий собственный вектор $\psi$ матрицы смежности, т.е. наибольшая $\lambda \in \mathbb {R}$ с соответствующими $\psi \in \mathbb {R} ^{n}$ такой, что $\psi A=\lambda \psi$. Тогда стохастическая матрица и стационарное распределение вероятностей имеют вид

$S_{ij}={\frac {A_{ij}}{\lambda }}{\frac {\psi _{j}}{\psi _{i}}}$

для которого каждый возможный путь длины $l$ из $i$-th к $j$-я вершина имеет вероятность

${\frac {1}{\lambda ^{l}}}{\frac {\psi _{j}}{\psi _{i}}}$.

Его уровень энтропии $\log(\lambda )$ и стационарное распределение вероятностей $\rho$ является

$\rho _{i}={\frac {\psi _{i}^{2}}{\|\psi \|_{2}^{2}}}$.

В отличие от GRW, вероятности перехода MERW обычно зависят от структуры всего графа (являются нелокальными). Следовательно, не следует представлять, что их непосредственно применяет ходок — если решения принимаются случайным образом, исходя из местной ситуации, как это сделал бы человек, подход GRW более уместен. MERW основан на принципе максимальной энтропии, что делает его самым безопасным предположением, когда у нас нет каких-либо дополнительных знаний о системе. Например, это было бы уместно для моделирования наших знаний об объекте, выполняющем некоторую сложную динамику – не обязательно случайную, как частица.

Эскиз вывода

Предположим для простоты, что рассматриваемый граф является ненаправленным, связным и апериодическим, что позволяет из теоремы Перрона–Фробениуса сделать вывод о единственности доминирующего собственного вектора. Следовательно $A^{l}$ может быть асимптотически ( $l\rightarrow \infty$) аппроксимируется $\lambda ^{l}\psi \psi ^{T}$ (или $\lambda ^{l}|\psi \rangle \langle \psi |$ в обозначениях бра-кет ).

MERW требует равномерного распределения по путям. Число $m_{il}$ путей длиной $2l$ и вершина $i$ в центре есть

$m_{il}=\sum _{j=1}^{n}\sum _{k=1}^{n}\left(A^{l}\right)_{ji}\left(A^{l}\right)_{ik}\approx \sum _{j=1}^{n}\sum _{k=1}^{n}\left(\lambda ^{l}\psi \psi ^{\top }\right)_{ji}\left(\lambda ^{l}\psi \psi ^{\top }\right)_{ik}=\sum _{j=1}^{n}\sum _{k=1}^{n}\lambda ^{2l}\psi _{j}\psi _{i}\psi _{i}\psi _{k}=\lambda ^{2l}\psi _{i}^{2}\underbrace {\sum _{j=1}^{n}\psi _{j}\sum _{k=1}^{n}\psi _{k}} _{=:b}$,

следовательно, для всех $i$,

$\rho _{i}=\lim _{l\rightarrow \infty }{\frac {m_{il}}{\sum \limits _{k=1}^{n}m_{kl}}}=\lim _{l\rightarrow \infty }{\frac {\lambda ^{2l}\psi _{i}^{2}b}{\sum \limits _{k=1}^{n}\lambda ^{2l}\psi _{k}^{2}b}}=\lim _{l\rightarrow \infty }{\frac {\psi _{i}^{2}}{\sum \limits _{k=1}^{n}\psi _{k}^{2}}}={\frac {\psi _{i}^{2}}{\sum \limits _{k=1}^{n}\psi _{k}^{2}}}={\frac {\psi _{i}^{2}}{\|\psi \|_{2}^{2}}}$.

Аналогично вычисляя распределение вероятностей для двух последовательных вершин, получаем, что вероятность оказаться в вершине $i$-я вершина и следующая за ней $j$-я вершина

${\frac {\psi _{i}A_{ij}\psi _{j}}{\sum \limits _{i'=1}^{n}\sum \limits _{j'=1}^{n}\psi _{i'}A_{i'j'}\psi _{j'}}}={\frac {\psi _{i}A_{ij}\psi _{j}}{\psi A\psi ^{\top }}}={\frac {\psi _{i}A_{ij}\psi _{j}}{\lambda \|\psi \|_{2}^{2}}}$.

Разделив на вероятность оказаться на $i$-я вершина, т.е. $\rho _{i}$, дает условную вероятность $S_{ij}$ принадлежащий $j$-я вершина, следующая после $i$-я вершина

$S_{ij}={\frac {A_{ij}}{\lambda }}{\frac {\psi _{j}}{\psi _{i}}}$.

Взвешенный MERW: ансамбль путей Больцмана

Мы предположили, что $A_{ij}\in \{0,1\}$ для MERW, соответствующего однородному ансамблю путей. Однако приведенный выше вывод работает для действительных неотрицательных $A$. Параметризация $A_{ij}=\exp(-E_{ij})$ и запрашиваем вероятность длины $l$ путь $(\gamma _{0},\ldots ,\gamma _{l})$, мы получаем:

${\textrm {Pr}}(\gamma _{0},\ldots ,\gamma _{l})=\rho _{\gamma _{0}}S_{\gamma _{0}\gamma _{1}}\ldots S_{\gamma _{l-1}\gamma _{l}}=\psi _{\gamma _{0}}{\frac {A_{\gamma _{0}\gamma _{1}}\ldots A_{\gamma _{l-1}\gamma _{l}}}{\lambda ^{l}}}\psi _{\gamma _{l}}=\psi _{\gamma _{0}}{\frac {\exp(-(E_{\gamma _{0}\gamma _{1}}+\ldots +E_{\gamma _{l-1}\gamma _{l}}))}{\lambda ^{l}}}\psi _{\gamma _{l}}$

Как и в распределении путей Больцмана для энергии, определяемом как сумма $E_{ij}$ по заданному пути. Например, это позволяет рассчитать распределение вероятностей закономерностей в модели Изинга .

Примеры

Слева: выбор оптимальной вероятности после символа 0 в кодировании Фибоначчи . Справа: одномерная дефектная решетка и ее стационарная плотность для длины 1000 цикла (имеет три дефекта). В то время как в стандартном случайном блуждании стационарная плотность пропорциональна степени вершины, что приводит здесь к разнице 3/2, в MERW плотность почти полностью локализована в наибольшей бездефектной области, аналогично основному состоянию , предсказанному квантовой механикой .

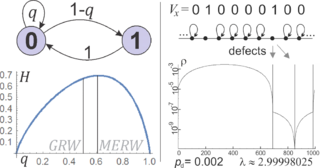
Давайте сначала рассмотрим простую нетривиальную ситуацию: кодирование Фибоначчи, когда мы хотим передать сообщение в виде последовательности 0 и 1, но не используя две последовательные единицы: после 1 должен быть 0. Чтобы максимизировать количество информации, передаваемой в такой последовательности, следует предположить равномерное распределение вероятностей в пространстве всех возможных последовательностей, удовлетворяющих этому ограничению. Чтобы практически использовать такие длинные последовательности, после 1 приходится использовать 0, но остается свобода выбора вероятности 0 после 0. Обозначим эту вероятность через $q$, то энтропийное кодирование позволит закодировать сообщение, используя выбранное распределение вероятностей. Стационарное распределение вероятностей символов для заданного $q$ оказывается $\rho =(1/(2-q),1-1/(2-q))$. Следовательно, производство энтропии $H(S)=\rho _{0}\left(q\log(1/q)+(1-q)\log(1/(1-q))\right)$, который максимизируется для $q=({\sqrt {5}}-1)/2\approx 0.618$, известное как золотое сечение . Напротив, стандартное случайное блуждание выберет неоптимальный вариант. $q=0.5$. Выбирая больший $q$ уменьшает количество информации, производимой после 0, а также уменьшает частоту 1, после чего мы не можем записать какую-либо информацию.

Более сложным примером является дефектная одномерная циклическая решетка: скажем, 1000 узлов соединены в кольцо, для которого все узлы, кроме дефектов, имеют петлю (ребро к себе). В стандартном случайном блуждании (GRW) стационарное распределение вероятностей будет иметь вероятность дефекта, составляющую 2/3 от вероятности вершин без дефектов - локализация почти отсутствует, также аналогично стандартной диффузии, которая является бесконечно малым пределом GRW. Для MERW нам нужно сначала найти доминирующий собственный вектор матрицы смежности – максимизируя $\lambda$ в:

$(\lambda \psi )_{x}=(A\psi )_{x}=\psi _{x-1}+(1-V_{x})\psi _{x}+\psi _{x+1}$

на все позиции $x$, где $V_{x}=1$ за дефекты, 0 в противном случае. Замена $3\psi _{x}$ и умножив уравнение на −1, получим:

$E\psi _{x}=-(\psi _{x-1}-2\psi _{x}+\psi _{x+1})+V_{x}\psi _{x}$

где $E=3-\lambda$ теперь минимизируется, становясь аналогом энергии. Формула внутри скобок представляет собой дискретный оператор Лапласа , что делает это уравнение дискретным аналогом стационарного уравнения Шредингера . Как и в квантовой механике, MERW предсказывает, что распределение вероятностей должно приводить точно к основному квантовому состоянию : $\rho _{x}\propto \psi _{x}^{2}$ с его сильно локализованной плотностью (в отличие от стандартной диффузии). Принимая бесконечно малый предел, мы можем получить стандартное непрерывное стационарное (независимое от времени) уравнение Шредингера ( $E\psi =-C\psi _{xx}+V\psi$ для $C=\hbar ^{2}/2m$) здесь.

См. также

• Принцип максимальной энтропии
• Центральность собственного вектора
• Цепь Маркова
• Локализация Андерсона

Внешние ссылки

• Габор Симони, Ю. Линь, З. Чжан, «Среднее время первого прохождения для случайных блужданий с максимальной энтропией в сложных сетях» . Научные отчеты, 2014.
• Модели электронной проводимости с использованием случайных блужданий с максимальной энтропией. Демонстрационный проект Wolfram