Уравнение Шрёдингера

Более общее введение в тему см. в разделе « Введение в квантовую механику» .

Уравнение Шредингера, начертанное на надгробии Аннемари и Эрвина Шредингеров. ( точечная запись Ньютона .) Для производной по времени используется

Уравнение Шрёдингера — это уравнение в частных производных , которое управляет волновой функцией квантовомеханической системы. Его открытие стало важной вехой в развитии квантовой механики . Оно названо в честь Эрвина Шредингера , который постулировал это уравнение в 1925 году и опубликовал его в 1926 году, что легло в основу работы, результатом которой стал его Нобелевская премия по физике в 1933 году.

Концептуально уравнение Шредингера является квантовым аналогом второго закона Ньютона в классической механике . Учитывая набор известных начальных условий, второй закон Ньютона делает математический прогноз относительно того, какой путь пойдет данная физическая система с течением времени. Уравнение Шредингера дает эволюцию во времени волновой функции , квантово-механической характеристики изолированной физической системы. Уравнение было постулировано Шредингером на основе постулата Луи де Бройля о том, что вся материя имеет связанную с ней волну материи . Уравнение предсказывало связанные состояния атома в соответствии с экспериментальными наблюдениями.

Уравнение Шрёдингера — не единственный способ изучать квантово-механические системы и делать предсказания. Другие формулировки квантовой механики включают матричную механику , введенную Вернером Гейзенбергом , и формулировку интеграла по траекториям , разработанную главным образом Ричардом Фейнманом . При сравнении этих подходов использование уравнения Шредингера иногда называют «волновой механикой». Уравнение Клейна-Гордона — это волновое уравнение , которое является релятивистской версией уравнения Шрёдингера. Уравнение Шрёдингера нерелятивистское, поскольку оно содержит первую производную по времени и вторую производную по пространству, и, следовательно, пространство и время не находятся в равных условиях.

Поль Дирак объединил специальную теорию относительности и квантовую механику в единую формулировку , которая упрощается до уравнения Шредингера в нерелятивистском пределе. Это уравнение Дирака , которое содержит единственную производную как в пространстве, так и во времени. УЧП со второй производной уравнения Клейна-Гордона привело к проблеме с плотностью вероятности, хотя это было релятивистское волновое уравнение . Плотность вероятности может быть отрицательной, что физически нежизнеспособно. Это было исправлено Дираком, взяв так называемый квадратный корень из оператора Клейна-Гордона и, в свою очередь, введя матрицы Дирака . В современном контексте уравнение Клейна-Гордона описывает частицы без спина , а уравнение Дирака описывает частицы со спином 1/2 .

Определение

Предварительные сведения

Комплексный график волновой функции , удовлетворяющей нерелятивистскому уравнению Шредингера с V = 0 . Подробнее см. волновой пакет.

Вводные курсы по физике или химии обычно знакомят с уравнением Шрёдингера таким образом, чтобы его можно было понять, зная только понятия и обозначения базового исчисления , особенно производных по пространству и времени. Особым случаем уравнения Шредингера, допускающим формулировку в этих терминах, является уравнение Шредингера в позиционном пространстве для одной нерелятивистской частицы в одном измерении: $$i\hbar {\frac {\partial }{\partial t}}\Psi (x,t)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}+V(x,t)\right]\Psi (x,t).$$Здесь, $\Psi (x,t)$ волновая функция, функция, которая присваивает комплексное число каждой точке $x$ в каждый момент времени $t$. Параметр $m$ - масса частицы, а $V(x,t)$ — это потенциал , который представляет среду, в которой существует частица. Константа $i$ – мнимая единица , а $\hbar$ — приведенная постоянная Планка , имеющая единицы действия ( энергия, умноженная на время).

Выйдя за рамки этого простого случая, математическая формулировка квантовой механики, разработанная Полем Дираком , Дэвид Хилберт , Джон фон Нейман , и Герман Вейль определяет состояние квантовомеханической системы как вектор $|\psi \rangle$ принадлежащий сепарабельному комплексному гильбертовому пространству ${\mathcal {H}}$. Постулируется, что этот вектор нормирован относительно внутреннего произведения гильбертова пространства, то есть в обозначениях Дирака он подчиняется $\langle \psi |\psi \rangle =1$. Точная природа этого гильбертова пространства зависит от системы - например, для описания положения и импульса гильбертово пространство представляет собой пространство функций, интегрируемых с квадратом. $L^{2}$, а гильбертово пространство для спина одиночного протона представляет собой двумерное комплексное векторное пространство $\mathbb {C} ^{2}$ с обычным внутренним продуктом.

Интересующие физические величины – положение, импульс, энергия, спин – представлены наблюдаемыми , которые являются самосопряженными операторами, действующими в гильбертовом пространстве. Волновая функция может быть собственным вектором наблюдаемой, и в этом случае она называется собственным состоянием , а связанное с ней собственное значение соответствует значению наблюдаемой в этом собственном состоянии. В более общем смысле, квантовое состояние представляет собой линейную комбинацию собственных состояний, известную как квантовая суперпозиция . Когда измеряется наблюдаемая величина, результатом будет одно из ее собственных значений с вероятностью, определяемой правилом Борна : в простейшем случае собственное значение $\lambda$ невырожден, а вероятность определяется выражением $|\langle \lambda |\psi \rangle |^{2}$, где $|\lambda \rangle$ является связанным с ним собственным вектором. В более общем смысле собственное значение вырождено, а вероятность определяется выражением $\langle \psi |P_{\lambda }|\psi \rangle$, где $P_{\lambda }$ является проектором на связанное с ним собственное пространство.

Собственное состояние импульса будет совершенно монохроматической волной бесконечной протяженности, которая не интегрируется с квадратом. Аналогично, собственное состояние положения будет дельта-распределением Дирака , не интегрируемым с квадратом и технически вообще не являющимся функцией. Следовательно, ни один из них не может принадлежать гильбертовому пространству частицы. Физики иногда рассматривают эти собственные состояния как «обобщенные собственные векторы» гильбертова пространства, состоящего из элементов вне этого пространства. Они используются для удобства вычислений и не представляют физические состояния. Таким образом, позиционно-пространственная волновая функция $\Psi (x,t)$ как использовано выше, может быть записано как внутренний продукт зависящего от времени вектора состояния $|\Psi (t)\rangle$ с нефизическими, но удобными «собственными состояниями положения» $|x\rangle$: $$\Psi (x,t)=\langle x|\Psi (t)\rangle .$$

Уравнение, зависящее от времени

Вид уравнения Шрёдингера зависит от физической ситуации. Наиболее общей формой является нестационарное уравнение Шрёдингера, которое описывает систему, развивающуюся во времени:

Зависящее от времени уравнение Шрёдингера   (общее)

$i\hbar {\frac {d}{dt}}\vert \Psi (t)\rangle ={\hat {H}}\vert \Psi (t)\rangle$

где $t$ это время, $\vert \Psi (t)\rangle$ – вектор состояния квантовой системы ( $\Psi$ греческая буква пси ), и ${\hat {H}}$ является наблюдаемой, гамильтоновым оператором .

Каждая из этих трех строк представляет собой волновую функцию, которая удовлетворяет зависящему от времени уравнению Шредингера для гармонического осциллятора . Слева: действительная часть (синий) и мнимая часть (красный) волновой функции. Справа: Распределение вероятности обнаружения частицы с этой волновой функцией в заданном положении. Две верхние строки представляют собой примеры стационарных состояний , соответствующих стоячим волнам . Нижний ряд представляет собой пример состояния, которое не является стационарным.

Термин «уравнение Шредингера» может относиться как к общему уравнению, так и к конкретной нерелятивистской версии. Общее уравнение действительно является довольно общим и используется во всей квантовой механике для всего, от уравнения Дирака до квантовой теории поля , путем включения различных выражений для гамильтониана. Конкретная нерелятивистская версия — это приближение, которое дает точные результаты во многих ситуациях, но только до определенной степени (см. релятивистскую квантовую механику и релятивистскую квантовую теорию поля ).

Чтобы применить уравнение Шредингера, запишите гамильтониан системы с учетом кинетической и потенциальной энергии частиц, составляющих систему, а затем подставьте его в уравнение Шредингера. Полученное уравнение в частных производных решается относительно волновой функции, содержащей информацию о системе. На практике квадрат абсолютного значения волновой функции в каждой точке принимается для определения функции плотности вероятности . Например, если задана волновая функция в позиционном пространстве $\Psi (x,t)$ как указано выше, у нас есть $$\Pr(x,t)=|\Psi (x,t)|^{2}.$$

Нестационарное уравнение

Описанное выше уравнение Шредингера, зависящее от времени, предсказывает, что волновые функции могут образовывать стоячие волны , называемые стационарными состояниями . Эти состояния особенно важны, поскольку их индивидуальное изучение в дальнейшем упрощает задачу решения нестационарного уравнения Шредингера для любого состояния. Стационарные состояния также можно описать более простой формой уравнения Шредингера - не зависящим от времени уравнением Шредингера.

Независимое от времени уравнение Шрёдингера ( общее )

$\operatorname {\hat {H}} |\Psi \rangle =E|\Psi \rangle$

где $E$ это энергия системы. Это используется только тогда, когда сам гамильтониан не зависит явно от времени. Однако даже в этом случае полная волновая функция зависит от времени, как объяснено в разделе о линейности ниже. На языке линейной алгебры это уравнение является уравнением на собственные значения . Следовательно, волновая функция является собственной функцией оператора Гамильтона с соответствующими собственными значениями $E$.

Характеристики

Линейность

Уравнение Шредингера представляет собой линейное дифференциальное уравнение , означающее, что если два вектора состояния $|\psi _{1}\rangle$ и $|\psi _{2}\rangle$ являются решениями, то и любая линейная комбинация $$|\psi \rangle =a|\psi _{1}\rangle +b|\psi _{2}\rangle$$двух векторов состояния, где a и b — любые комплексные числа. Более того, сумму можно расширить на любое количество векторов состояния. Это свойство позволяет суперпозициям квантовых состояний быть решениями уравнения Шрёдингера. В более общем плане считается, что общее решение уравнения Шрёдингера можно найти, взяв взвешенную сумму по базису состояний. Часто используемый выбор - это основа собственных состояний энергии , которые являются решениями независимого от времени уравнения Шредингера. В этом базисе зависящий от времени вектор состояния $|\Psi (t)\rangle$ можно записать как линейную комбинацию $$|\Psi (t)\rangle =\sum _{n}A_{n}e^{{-iE_{n}t}/\hbar }|\psi _{E_{n}}\rangle ,$$где $A_{n}$ комплексные числа и векторы $|\psi _{E_{n}}\rangle$ являются решениями нестационарного уравнения ${\hat {H}}|\psi _{E_{n}}\rangle =E_{n}|\psi _{E_{n}}\rangle$.

Унитарность

Дополнительная информация: теорема Вигнера и теорема Стоуна.

Удерживая гамильтониан ${\hat {H}}$ постоянная, уравнение Шрёдингера имеет решение $$|\Psi (t)\rangle =e^{-i{\hat {H}}t/\hbar }|\Psi (0)\rangle .$$Оператор ${\hat {U}}(t)=e^{-i{\hat {H}}t/\hbar }$ известен как оператор временной эволюции, и он унитарен : он сохраняет скалярное произведение между векторами в гильбертовом пространстве. Унитарность - это общая особенность эволюции во времени согласно уравнению Шредингера. Если исходное состояние $|\Psi (0)\rangle$, то состояние позже $t$ будет предоставлен $$|\Psi (t)\rangle ={\hat {U}}(t)|\Psi (0)\rangle$$для некоторого унитарного оператора ${\hat {U}}(t)$. Обратно, предположим, что ${\hat {U}}(t)$ представляет собой непрерывное семейство унитарных операторов, параметризованное $t$. Не умаляя общности , параметризацию можно выбрать так, чтобы ${\hat {U}}(0)$ является оператором идентификации и что ${\hat {U}}(t/N)^{N}={\hat {U}}(t)$ для любого $N>0$. Затем ${\hat {U}}(t)$ зависит от параметра $t$ таким образом, что $${\hat {U}}(t)=e^{-i{\hat {G}}t}$$для некоторого самосопряженного оператора ${\hat {G}}$, называемый генератором семейства ${\hat {U}}(t)$. равен 1 Гамильтониан является именно таким генератором (с точностью до коэффициента постоянной Планка, который в натуральных единицах ).Чтобы увидеть, что генератор является эрмитовым, обратите внимание, что при ${\hat {U}}(\delta t)\approx {\hat {U}}(0)-i{\hat {G}}\delta t$, у нас есть $${\hat {U}}(\delta t)^{\dagger }{\hat {U}}(\delta t)\approx ({\hat {U}}(0)^{\dagger }+i{\hat {G}}^{\dagger }\delta t)({\hat {U}}(0)-i{\hat {G}}\delta t)=I+i\delta t({\hat {G}}^{\dagger }-{\hat {G}})+O(\delta t^{2}),$$ так ${\hat {U}}(t)$ унитарна только в том случае, если в первом порядке ее производная эрмитова.

Изменения базы

Уравнение Шредингера часто представляется с использованием величин, изменяющихся в зависимости от положения, но как векторно-операторное уравнение оно имеет допустимое представление в любом произвольном полном базисе кетов в гильбертовом пространстве . Как упоминалось выше, для вычислительных целей используются также «базисы», лежащие вне физического гильбертова пространства. Это иллюстрируется уравнениями Шредингера в позиционном пространстве и импульсном пространстве для нерелятивистской бесспиновой частицы. Гильбертово пространство для такой частицы представляет собой пространство комплексных функций, интегрируемых с квадратом в трехмерном евклидовом пространстве, а его гамильтониан представляет собой сумму члена кинетической энергии, квадратичного по оператору импульса, и члена потенциальной энергии: $$i\hbar {\frac {d}{dt}}|\Psi (t)\rangle =\left({\frac {1}{2m}}{\hat {p}}^{2}+{\hat {V}}\right)|\Psi (t)\rangle .$$Письмо $\mathbf {r}$ для трехмерного вектора положения и $\mathbf {p}$ для трехмерного вектора импульса уравнение Шредингера в позиционном пространстве имеет вид $$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,t).$$Аналог в импульсном пространстве включает преобразования Фурье волновой функции и потенциала: $$i\hbar {\frac {\partial }{\partial t}}{\tilde {\Psi }}(\mathbf {p} ,t)={\frac {\mathbf {p} ^{2}}{2m}}{\tilde {\Psi }}(\mathbf {p} ,t)+(2\pi \hbar )^{-3/2}\int d^{3}\mathbf {p} '\,{\tilde {V}}(\mathbf {p} -\mathbf {p} '){\tilde {\Psi }}(\mathbf {p} ',t).$$Функции $\Psi (\mathbf {r} ,t)$ и ${\tilde {\Psi }}(\mathbf {p} ,t)$ получены из $|\Psi (t)\rangle$ к $$\Psi (\mathbf {r} ,t)=\langle \mathbf {r} |\Psi (t)\rangle ,$$$${\tilde {\Psi }}(\mathbf {p} ,t)=\langle \mathbf {p} |\Psi (t)\rangle ,$$где $|\mathbf {r} \rangle$ и $|\mathbf {p} \rangle$ не принадлежат самому гильбертовому пространству, но имеют четко определенные внутренние произведения со всеми элементами этого пространства.

При ограничении трех измерений одним измерением уравнение позиционного пространства представляет собой лишь первую форму уравнения Шредингера, приведенного выше . Связь между положением и импульсом в квантовой механике можно оценить в одном измерении. При каноническом квантовании классические переменные $x$ и $p$ повышаются до самосопряженных операторов ${\hat {x}}$ и ${\hat {p}}$ которые удовлетворяют каноническому коммутационному соотношению $$[{\hat {x}},{\hat {p}}]=i\hbar .$$Это означает, что $$\langle x|{\hat {p}}|\Psi \rangle =-i\hbar {\frac {d}{dx}}\Psi (x),$$поэтому действие оператора импульса ${\hat {p}}$ в представлении в позиционном пространстве ${\textstyle -i\hbar {\frac {d}{dx}}}$. Таким образом, ${\hat {p}}^{2}$ становится второй производной , а в трех измерениях вторая производная становится лапласианом $\nabla ^{2}$.

Каноническое коммутационное соотношение также подразумевает, что операторы положения и импульса являются Фурье-сопряженными друг с другом. Следовательно, функции, первоначально определенные в терминах зависимости от положения, можно преобразовать в функции импульса с помощью преобразования Фурье. В физике твердого тела уравнение Шредингера часто записывается для функций импульса, поскольку теорема Блоха обеспечивает периодические потенциальные пары кристаллической решетки. ${\tilde {\Psi }}(p)$ с ${\tilde {\Psi }}(p+K)$ только для дискретных обратной решетки векторов $K$. Это делает удобным решение уравнения Шредингера в импульсном пространстве в каждой точке зоны Бриллюэна независимо от других точек зоны Бриллюэна.

Вероятностный ток

Основные статьи: Вероятностный ток и уравнение непрерывности

Уравнение Шредингера согласуется с локальным сохранением вероятности . Это также гарантирует, что нормированная волновая функция остается нормированной после эволюции во времени. В матричной механике это означает, что оператор эволюции во времени является унитарным оператором . В отличие, например, от уравнения Клейна Гордона, хотя переопределенный внутренний продукт волновой функции может быть независимым от времени, общий объемный интеграл от квадрата модуля волновой функции не обязательно должен быть независимым от времени.

Уравнение непрерывности вероятности в нерелятивистской квантовой механике формулируется как: $${\frac {\partial }{\partial t}}\rho \left(\mathbf {r} ,t\right)+\nabla \cdot \mathbf {j} =0,$$где $$\mathbf {j} ={\frac {1}{2m}}\left(\Psi ^{*}{\hat {\mathbf {p} }}\Psi -\Psi {\hat {\mathbf {p} }}\Psi ^{*}\right)=-{\frac {i\hbar }{2m}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})={\frac {\hbar }{m}}\operatorname {Im} (\psi ^{*}\nabla \psi )$$— ток вероятности или поток вероятности (поток на единицу площади).

Если волновую функцию представить в виде ${\textstyle \psi ({\bf {x}},t)={\sqrt {\rho ({\bf {x}},t)}}\exp \left({\frac {iS({\bf {x}},t)}{\hbar }}\right),}$ где $S(\mathbf {x} ,t)$ — действительная функция, представляющая комплексную фазу волновой функции, то поток вероятности рассчитывается как: $$\mathbf {j} ={\frac {\rho \nabla S}{m}}$$Следовательно, говорят, что пространственное изменение фазы волновой функции характеризует поток вероятности волновой функции. Хотя ${\textstyle {\frac {\nabla S}{m}}}$ Этот термин, по-видимому, играет роль скорости, он не представляет скорость в точке, поскольку одновременное измерение положения и скорости нарушает принцип неопределенности .

Разделение переменных

Если гамильтониан не является явной функцией времени, уравнение Шрёдингера выглядит следующим образом: $$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right]\Psi (\mathbf {r} ,t).$$ Оператор слева зависит только от времени; тот, что справа, зависит только от пространства.Решение уравнения путем разделения переменных означает поиск решения вида произведения пространственной и временной частей. $$\Psi (\mathbf {r} ,t)=\psi (\mathbf {r} )\tau (t),$$где $\psi (\mathbf {r} )$ является функцией всех пространственных координат(ы) частицы(ов), составляющих только систему, и $\tau (t)$ является функцией только времени. Подставив это выражение на $\Psi$ в зависящую от времени левую часть показывает, что $\tau (t)$ – фазовый коэффициент: $$\Psi (\mathbf {r} ,t)=\psi (\mathbf {r} )e^{-i{Et/\hbar }}.$$Решение такого типа называется стационарным, поскольку единственной зависимостью от времени является фазовый множитель, который сокращается при расчете плотности вероятности по правилу Борна.

Пространственная часть полной волновой функции решает: $$\nabla ^{2}\psi (\mathbf {r} )+{\frac {2m}{\hbar ^{2}}}\left[E-V(\mathbf {r} )\right]\psi (\mathbf {r} )=0.$$где энергия $E$ появляется в фазовом коэффициенте.

Это распространяется на любое количество частиц в любом количестве измерений (в независимом от времени потенциале): решениями стоячей волны независимого от времени уравнения являются состояния с определенной энергией, а не распределение вероятностей различных энергий. В физике эти стоячие волны называются « стационарными состояниями » или « собственными состояниями энергии »; в химии их называют « атомными орбиталями » или « молекулярными орбиталями ». Суперпозиции собственных состояний энергии изменяют свои свойства в зависимости от относительных фаз между уровнями энергии. Собственные состояния энергии составляют основу: любая волновая функция может быть записана как сумма по дискретным энергетическим состояниям или как интеграл по непрерывным энергетическим состояниям, или, в более общем смысле, как интеграл по мере. Это спектральная теорема в математике, и в конечномерном пространстве состояний это просто утверждение полноты собственных векторов эрмитовой матрицы .

Разделение переменных также может быть полезным методом для независимого от времени уравнения Шредингера. Например, в зависимости от симметрии задачи декартовы оси могут быть разделены: $$\psi (\mathbf {r} )=\psi _{x}(x)\psi _{y}(y)\psi _{z}(z),$$или радиальные и угловые координаты могут быть разделены: $$\psi (\mathbf {r} )=\psi _{r}(r)\psi _{\theta }(\theta )\psi _{\phi }(\phi ).$$

Примеры

Смотрите также: Список квантовомеханических систем с аналитическими решениями.

Частица в коробке

Одномерный ящик потенциальной энергии (или бесконечная потенциальная яма)

Основная статья: Частица в коробке

Частица в одномерном ящике потенциальной энергии является наиболее математически простым примером, когда ограничения приводят к квантованию уровней энергии. Ящик определяется как имеющий нулевую потенциальную энергию внутри определенной области и бесконечную потенциальную энергию снаружи . Для одномерного случая в $x$ направлении, независимое от времени уравнение Шредингера может быть записано $$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi .$$

С дифференциальным оператором, определенным формулой $${\hat {p}}_{x}=-i\hbar {\frac {d}{dx}}$$предыдущее уравнение напоминает классический аналог кинетической энергии , $${\frac {1}{2m}}{\hat {p}}_{x}^{2}=E,$$с государством $\psi$ в этом случае имея энергию $E$ совпадает с кинетической энергией частицы.

Общие решения уравнения Шредингера для частицы в ящике: $$\psi (x)=Ae^{ikx}+Be^{-ikx}\qquad \qquad E={\frac {\hbar ^{2}k^{2}}{2m}}$$или, по формуле Эйлера , $$\psi (x)=C\sin(kx)+D\cos(kx).$$

Бесконечные потенциальные стенки ящика определяют значения $C,D,$ и $k$ в $x=0$ и $x=L$ где $\psi$ должно быть равно нулю. Таким образом, при $x=0$, $$\psi (0)=0=C\sin(0)+D\cos(0)=D$$и $D=0$. В $x=L$, $$\psi (L)=0=C\sin(kL),$$в котором $C$ не может быть нулевым, поскольку это противоречило бы постулату о том, что $\psi$ имеет норму 1. Следовательно, поскольку $\sin(kL)=0$, $kL$ должно быть целым числом, кратным $\pi$, $$k={\frac {n\pi }{L}}\qquad \qquad n=1,2,3,\ldots .$$

Это ограничение на $k$ подразумевает ограничение на уровни энергии, что дает $$E_{n}={\frac {\hbar ^{2}\pi ^{2}n^{2}}{2mL^{2}}}={\frac {n^{2}h^{2}}{8mL^{2}}}.$$

Конечная потенциальная яма — это обобщение проблемы бесконечной потенциальной ямы на потенциальные ямы конечной глубины. Задача о конечной потенциальной яме математически более сложна, чем задача о бесконечной частице в ящике, поскольку волновая функция не привязана к нулю на стенках ямы. Вместо этого волновая функция должна удовлетворять более сложным математическим граничным условиям, поскольку она отлична от нуля в областях вне ямы. Другой связанной с этим проблемой является проблема прямоугольного потенциального барьера , который обеспечивает модель эффекта квантового туннелирования , который играет важную роль в работе современных технологий, таких как флэш-память и сканирующая туннельная микроскопия .

Гармонический осциллятор

Гармонический осциллятор в классической механике (A–B) и квантовой механике (C–H). В (A–B) шарик, прикрепленный к пружине , колеблется вперед и назад. (C – H) – шесть решений уравнения Шредингера для этой ситуации. Горизонтальная ось — это положение, вертикальная ось — действительная (синяя) или мнимая часть (красная) волновой функции . Стационарные состояния или собственные состояния энергии, которые являются решениями независимого от времени уравнения Шрёдингера, показаны в C, D, E, F, но не G или H.

Основная статья: Квантовый гармонический осциллятор

Уравнение Шредингера для этой ситуации имеет вид $$E\psi =-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi +{\frac {1}{2}}m\omega ^{2}x^{2}\psi ,$$где $x$ это смещение и $\omega$ угловая частота. Кроме того, его можно использовать для приблизительного описания широкого спектра других систем, включая колеблющиеся атомы, молекулы и т. д. и атомы или ионы в решетках, и аппроксимация других потенциалов вблизи точек равновесия. Это также основа методов возмущений в квантовой механике.

Решения в позиционном пространстве: $$\psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\ \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\ e^{-{\frac {m\omega x^{2}}{2\hbar }}}\ {\mathcal {H}}_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right),$$где $n\in \{0,1,2,\ldots \}$, а функции ${\mathcal {H}}_{n}$ являются полиномами Эрмита порядка $n$. Набор решений может быть создан с помощью $$\psi _{n}(x)={\frac {1}{\sqrt {n!}}}\left({\sqrt {\frac {m\omega }{2\hbar }}}\right)^{n}\left(x-{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)^{n}\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{\frac {-m\omega x^{2}}{2\hbar }}.$$

Собственные значения $$E_{n}=\left(n+{\frac {1}{2}}\right)\hbar \omega .$$

Дело $n=0$ называется основным состоянием , его энергия называется энергией нулевой точки , а волновая функция является гауссовой .

Гармонический осциллятор, подобно частице в ящике, иллюстрирует общую особенность уравнения Шрёдингера, состоящую в том, что энергии связанных собственных состояний дискретизированы.

Атом водорода

Волновые функции в электрона атоме водорода на разных энергетических уровнях . Они построены в соответствии с решениями уравнения Шредингера.

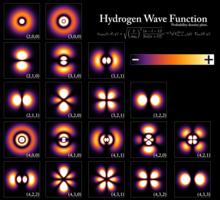
Уравнение Шредингера для электрона в атоме водорода (или водородоподобном атоме) имеет вид $$E\psi =-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}\psi -{\frac {q^{2}}{4\pi \varepsilon _{0}r}}\psi$$где $q$ - заряд электрона, $\mathbf {r}$ - положение электрона относительно ядра, $r=|\mathbf {r} |$ — величина относительного положения, потенциальный член обусловлен кулоновским взаимодействием , где $\varepsilon _{0}$ диэлектрическая проницаемость свободного пространства и $$\mu ={\frac {m_{q}m_{p}}{m_{q}+m_{p}}}$$ двумя телами , равная - это приведенная масса водорода ядра (просто протона ) с $m_{p}$ и электрон массы $m_{q}$. Отрицательный знак возникает в потенциальном члене, поскольку протон и электрон заряжены противоположно. Приведенная масса вместо массы электрона используется, поскольку электрон и протон вместе вращаются вокруг общего центра масс и представляют собой задачу двух тел, которую необходимо решить. Принципиальный интерес здесь представляет движение электрона, поэтому эквивалентной задачей одного тела является движение электрона с использованием приведенной массы.

Уравнение Шрёдингера для атома водорода можно решить методом разделения переменных. В этом случае сферические полярные координаты наиболее удобными являются . Таким образом, $$\psi (r,\theta ,\varphi )=R(r)Y_{\ell }^{m}(\theta ,\varphi )=R(r)\Theta (\theta )\Phi (\varphi ),$$где R — радиальные функции и $Y_{l}^{m}(\theta ,\varphi )$ являются сферическими гармониками степени $\ell$ и заказать $m$. Это единственный атом, для которого уравнение Шрёдингера решено точно. Многоэлектронные атомы требуют приближенных методов. Семейство решений: $$\psi _{n\ell m}(r,\theta ,\varphi )={\sqrt {\left({\frac {2}{na_{0}}}\right)^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\varphi )$$где

• $a_{0}={\frac {4\pi \varepsilon _{0}\hbar ^{2}}{m_{q}q^{2}}}$ – радиус Бора ,
• $L_{n-\ell -1}^{2\ell +1}(\cdots )$ являются обобщенными полиномами Лагерра степени $n-\ell -1$,
• $n,\ell ,m$ — главное , азимутальное и магнитное квантовые числа соответственно, которые принимают значения $n=1,2,3,\dots ,$ $\ell =0,1,2,\dots ,n-1,$ $m=-\ell ,\dots ,\ell .$

Примерные решения

Обычно невозможно точно решить уравнение Шредингера для ситуаций, представляющих физический интерес. Соответственно, приближенные решения получаются с использованием таких методов, как вариационные методы и аппроксимация ВКБ . Также принято рассматривать интересующую проблему как небольшую модификацию проблемы, которая может быть решена точно, с помощью метода, известного как теория возмущений .

Полуклассический предел

Один из простых способов сравнить классическую механику с квантовой — это рассмотреть эволюцию во времени ожидаемого положения и ожидаемого импульса, которую затем можно сравнить с эволюцией во времени обычного положения и импульса в классической механике. Значения квантового ожидания удовлетворяют теореме Эренфеста . Для одномерной квантовой частицы, движущейся в потенциале $V$, теорема Эренфеста гласит $$m{\frac {d}{dt}}\langle x\rangle =\langle p\rangle ;\quad {\frac {d}{dt}}\langle p\rangle =-\left\langle V'(X)\right\rangle .$$Хотя первое из этих уравнений согласуется с классическим поведением, второе — нет: если пара $(\langle X\rangle ,\langle P\rangle )$ если бы удовлетворялся второй закон Ньютона, правая часть второго уравнения должна была бы быть равна $$-V'\left(\left\langle X\right\rangle \right)$$что обычно не совпадает с $-\left\langle V'(X)\right\rangle$. Для генерала $V'$Следовательно, квантовая механика может привести к предсказаниям, в которых ожидаемые значения не имитируют классическое поведение. Однако в случае квантового гармонического осциллятора $V'$ является линейным, и это различие исчезает, так что в этом особом случае ожидаемое положение и ожидаемый импульс точно следуют классическим траекториям.

Для общих систем лучшее, на что мы можем надеяться, — это то, что ожидаемое положение и импульс будут примерно следовать классическим траекториям. Если волновая функция сильно сконцентрирована вокруг точки $x_{0}$, затем $V'\left(\left\langle X\right\rangle \right)$ и $\left\langle V'(X)\right\rangle$ будет почти одинаковым, так как оба будут примерно равны $V'(x_{0})$. В этом случае ожидаемое положение и ожидаемый импульс останутся очень близкими к классическим траекториям, по крайней мере, до тех пор, пока волновая функция остается сильно локализованной по положению.

Уравнение Шрёдингера в общем виде $$i\hbar {\frac {\partial }{\partial t}}\Psi \left(\mathbf {r} ,t\right)={\hat {H}}\Psi \left(\mathbf {r} ,t\right)$$тесно связано с уравнением Гамильтона – Якоби (HJE) $$-{\frac {\partial }{\partial t}}S(q_{i},t)=H\left(q_{i},{\frac {\partial S}{\partial q_{i}}},t\right)$$где $S$ это классическое действие и $H$ — функция Гамильтона (не оператор). Здесь обобщенные координаты $q_{i}$ для $i=1,2,3$ (используется в контексте HJE) может быть установлено в положение в декартовых координатах как $\mathbf {r} =(q_{1},q_{2},q_{3})=(x,y,z)$.

Замена $$\Psi ={\sqrt {\rho (\mathbf {r} ,t)}}e^{iS(\mathbf {r} ,t)/\hbar }$$где $\rho$ - плотность вероятности, в уравнение Шредингера, а затем переходя к пределу $\hbar \to 0$ в полученном уравнении получим уравнение Гамильтона–Якоби .

Матрицы плотности

Основная статья: Матрица плотности

Волновые функции не всегда являются наиболее удобным способом описания квантовых систем и их поведения. Когда подготовка системы известна лишь частично или когда исследуемая система является частью более крупного целого, матрицы плотности . вместо этого можно использовать Матрица плотности — это положительный полуопределенный оператор, которого след равен 1. (Также используется термин «оператор плотности», особенно когда основное гильбертово пространство бесконечномерно.) Множество всех матриц плотности выпукло и крайние точки — это операторы, проектирующие на векторы в гильбертовом пространстве. Это представления волновых функций в матрице плотности; в обозначениях Дирака они записываются $${\hat {\rho }}=|\Psi \rangle \langle \Psi |.$$

Аналог уравнения Шредингера для волновых функций в матрице плотности: $$i\hbar {\frac {\partial {\hat {\rho }}}{\partial t}}=[{\hat {H}},{\hat {\rho }}],$$где скобки обозначают коммутатор . Оно известно как уравнение фон Неймана, уравнение Лиувилля – фон Неймана или просто уравнение Шрёдингера для матриц плотности. Если гамильтониан не зависит от времени, это уравнение можно легко решить и получить $${\hat {\rho }}(t)=e^{-i{\hat {H}}t/\hbar }{\hat {\rho }}(0)e^{i{\hat {H}}t/\hbar }.$$

В более общем смысле, если унитарный оператор ${\hat {U}}(t)$ описывает эволюцию волновой функции на некотором интервале времени, то временная эволюция матрицы плотности на этом же интервале определяется выражением $${\hat {\rho }}(t)={\hat {U}}(t){\hat {\rho }}(0){\hat {U}}(t)^{\dagger }.$$

Унитарная эволюция матрицы плотности сохраняет ее энтропию фон Неймана .

Релятивистская квантовая физика и квантовая теория поля

Описанное выше одночастичное уравнение Шредингера справедливо по существу в нерелятивистской области. По одной из причин, он по существу инвариантен относительно преобразований Галилея , которые образуют группу симметрии ньютоновской динамики . Более того, процессы, которые изменяют количество частиц, естественны в теории относительности, и поэтому уравнение для одной частицы (или любого фиксированного их числа) может иметь лишь ограниченное применение. Более общую форму уравнения Шредингера, которая также применяется в релятивистских ситуациях, можно сформулировать в рамках квантовой теории поля (КТП), структуры, которая позволяет сочетать квантовую механику со специальной теорией относительности. Область, в которой оба одновременно применимы, может быть описана релятивистской квантовой механикой . В таких описаниях может использоваться временная эволюция, генерируемая гамильтоновым оператором, как в функциональном методе Шредингера .

Уравнения Клейна–Гордона и Дирака.

Попытки объединить квантовую физику со специальной теорией относительности начались с построения релятивистских волновых уравнений на основе релятивистского соотношения энергии и импульса. $$E^{2}=(pc)^{2}+\left(m_{0}c^{2}\right)^{2},$$вместо нерелятивистских уравнений энергии. Уравнение Клейна-Гордона и уравнение Дирака являются двумя такими уравнениями. Уравнение Клейна – Гордона, $$-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi +\nabla ^{2}\psi ={\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi ,$$было первым таким уравнением, полученным еще до нерелятивистского одночастичного уравнения Шредингера, и оно применимо к массивным бесспиновым частицам. Исторически Дирак получил уравнение Дирака, ища дифференциальное уравнение, которое было бы первого порядка как во времени, так и в пространстве, что является желательным свойством для релятивистской теории. Чтобы извлечь таким образом «квадратный корень» из левой части уравнения Клейна – Гордона, потребовалось разложить его на фактор в произведение двух операторов, которое Дирак написал, используя матрицы 4 × 4. $\alpha _{1},\alpha _{2},\alpha _{3},\beta$. Следовательно, волновая функция также стала четырехкомпонентной функцией, подчиняющейся уравнению Дирака, которое в свободном пространстве имеет вид $$\left(\beta mc^{2}+c\left(\sum _{n\mathop {=} 1}^{3}\alpha _{n}p_{n}\right)\right)\psi =i\hbar {\frac {\partial \psi }{\partial t}}.$$

Это снова имеет форму уравнения Шредингера, где производная по времени волновой функции задается гамильтоновым оператором, действующим на волновую функцию. Учет влияния на частицу требует модификации оператора Гамильтона. Например, гамильтониан Дирака для частицы массы m и электрического заряда q в электромагнитном поле (описываемом электромагнитными потенциалами φ и A ): $${\hat {H}}_{\text{Dirac}}=\gamma ^{0}\left[c{\boldsymbol {\gamma }}\cdot \left({\hat {\mathbf {p} }}-q\mathbf {A} \right)+mc^{2}+\gamma ^{0}q\varphi \right],$$в котором γ = ( γ ¹ , с ² , с ³ ) и γ ⁰ Дирака – гамма-матрицы , связанные со спином частицы. Уравнение Дирака справедливо для всех спин- 1/2 , частицы , а решениями уравнения являются 4-компонентные спинорные поля две из которых соответствуют частице, а две другие — античастице .

Для уравнения Клейна–Гордона общая форма уравнения Шредингера неудобна в использовании, и на практике гамильтониан не выражается аналогично гамильтониану Дирака. Уравнения для релятивистских квантовых полей, двумя примерами которых являются уравнения Клейна-Гордона и Дирака, можно получить другими способами, например, исходя из лагранжевой плотности и используя уравнения Эйлера-Лагранжа для полей или используя теорию представлений группа Лоренца , в которой определенные представления можно использовать для фиксации уравнения для свободной частицы заданного спина (и массы).

В общем, гамильтониан, который следует подставить в общее уравнение Шредингера, является не только функцией операторов положения и импульса (и, возможно, времени), но также и спиновых матриц. Кроме того, решения релятивистского волнового уравнения для массивной частицы со спином s представляют собой комплексные 2(2 s + 1) -компонентные спинорные поля .

Фокское пространство

В первоначальной формулировке уравнение Дирака представляет собой уравнение для одной квантовой частицы, точно так же, как одночастичное уравнение Шредингера с волновой функцией. $\Psi (x,t)$. Это имеет ограниченное применение в релятивистской квантовой механике, где число частиц не фиксировано. Эвристически это усложнение можно мотивировать, отметив, что эквивалентность массы и энергии подразумевает, что материальные частицы могут быть созданы из энергии. Распространенный способ решить эту проблему в КТП — ввести гильбертово пространство, в котором базисные состояния помечены числом частиц, так называемое пространство Фока . Затем можно сформулировать уравнение Шрёдингера для квантовых состояний в этом гильбертовом пространстве. Однако, поскольку уравнение Шрёдингера выбирает предпочтительную ось времени, лоренц-инвариантность теории больше не проявляется, и, соответственно, теорию часто формулируют другими способами.

История

Основная статья: Теоретическое и экспериментальное обоснование уравнения Шрёдингера

Эрвин Шрёдингер

Следуя Макса Планка квантованию света (см. «Излучение черного тела» ), Альберт Эйнштейн Планка интерпретировал кванты как фотоны , частицы света , и предположил, что энергия фотона пропорциональна его частоте , что является одним из первых признаков волны . – двойственность частиц . Поскольку энергия и импульс связаны так же, как частота и волновое число в специальной теории относительности , отсюда следует, что импульс $p$ фотона обратно пропорциональна его длине волны $\lambda$, или пропорционально его волновому числу $k$: $$p={\frac {h}{\lambda }}=\hbar k,$$где $h$ Планка постоянная и $\hbar ={h}/{2\pi }$ – приведенная постоянная Планка. Луи де Бройль предположил, что это верно для всех частиц, даже для частиц, имеющих массу, например электронов. Он показал, что, если предположить, что волны материи распространяются вместе со своими аналогами-частицами, электроны образуют стоячие волны , а это означает, что разрешены только определенные дискретные частоты вращения вокруг ядра атома. Эти квантованные орбиты соответствуют дискретным уровням энергии , и де Бройль воспроизвел формулу модели Бора для энергетических уровней. Модель Бора была основана на предположении о квантовании углового момента $L$ в соответствии с $$L=n{\frac {h}{2\pi }}=n\hbar .$$По мнению де Бройля, электрон описывается волной, и по окружности орбиты электрона должно уместиться целое число длин волн: $$n\lambda =2\pi r.$$

Этот подход по существу ограничивал электронную волну в одном измерении, вдоль круговой орбиты радиуса $r$.

В 1921 году, до де Бройля, Артур К. Ланн из Чикагского университета использовал тот же аргумент, основанный на пополнении релятивистского 4-вектора энергии-импульса , чтобы вывести то, что мы теперь называем соотношением де Бройля. В отличие от де Бройля, Ланн сформулировал дифференциальное уравнение, теперь известное как уравнение Шредингера, и нашел его собственные значения энергии для атома водорода; статья была отклонена журналом Physical Review . По словам Кеймена,

Развивая идеи де Бройля, физик Питер Дебай сделал небрежное замечание, что, если частицы ведут себя как волны, они должны удовлетворять некоторому волновому уравнению. Вдохновленный замечанием Дебая, Шредингер решил найти правильное трехмерное волновое уравнение для электрона. Он руководствовался аналогией Уильяма Роуэна Гамильтона между механикой и оптикой , закодированной в наблюдении, что предел нулевой длины волны оптики напоминает механическую систему — траектории световых лучей становятся острыми дорожками, подчиняющимися принципу Ферма , аналогу принципа наименьшего действия .

Уравнение, которое он нашел, $$i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi (\mathbf {r} ,t)+V(\mathbf {r} )\Psi (\mathbf {r} ,t).$$

К этому времени Арнольд Зоммерфельд уточнил модель Бора с помощью релятивистских поправок . Шредингер использовал релятивистское соотношение энергии-импульса, чтобы найти то, что сейчас известно как уравнение Клейна-Гордона в кулоновском потенциале (в натуральных единицах ): $$\left(E+{\frac {e^{2}}{r}}\right)^{2}\psi (x)=-\nabla ^{2}\psi (x)+m^{2}\psi (x).$$

Он нашел стоячие волны этого релятивистского уравнения, но релятивистские поправки не согласовывались с формулой Зоммерфельда. Обескураженный, он отложил свои расчеты и в декабре 1925 года уединился с любовницей в горной хижине.

Находясь в хижине, Шредингер решил, что его ранние нерелятивистские расчеты достаточно новы, чтобы их можно было опубликовать, и решил оставить проблему релятивистских поправок на будущее. Несмотря на трудности с решением дифференциального уравнения для водорода (он обратился за помощью к своему другу математику Герману Вейлю В статье, опубликованной в 1926 году, Шредингер показал, что его нерелятивистская версия волнового уравнения дает правильные спектральные энергии водорода. Шредингер вычислил спектральную серию водорода , рассматривая водорода атома электрон как волну. $\Psi (\mathbf {x} ,t)$, двигаясь в потенциальной яме $V$, созданный протоном . Это вычисление точно воспроизвело уровни энергии модели Бора .

Уравнение Шрёдингера детализирует поведение $\Psi$ но ничего не говорит о его природе . Шрёдингер пытался интерпретировать реальную часть $\Psi {\frac {\partial \Psi ^{*}}{\partial t}}$ как плотность заряда, а затем пересмотрел это предложение, заявив в своей следующей статье, что квадрат модуля $\Psi$ это плотность заряда. Однако этот подход не увенчался успехом. В 1926 году, всего через несколько дней после публикации этой статьи, Макс Борн успешно интерпретировал $\Psi$ как амплитуда вероятности , квадрат модуля которой равен плотности вероятности . Позже сам Шредингер объяснил эту интерпретацию следующим образом:

Уже упомянутая пси-функция.... теперь является средством прогнозирования вероятности результатов измерений. В нем воплощена мгновенно достигнутая сумма теоретически обоснованных будущих ожиданий, что-то вроде изложенной в каталоге.

— Эрвин Шрёдингер

Интерпретация

Основная статья: Интерпретации квантовой механики

Уравнение Шрёдингера позволяет рассчитать волновую функцию системы и понять, как она динамически изменяется во времени. Однако уравнение Шредингера прямо не говорит , что такое волновая функция. Смысл уравнения Шредингера и то, как математические объекты в нем связаны с физической реальностью, зависят от интерпретации квантовой механики принятой .

Согласно взглядам, которые часто объединяются в Копенгагенскую интерпретацию , волновая функция системы представляет собой набор статистической информации об этой системе. Уравнение Шрёдингера связывает информацию о системе в один момент времени с информацией о ней в другой момент. Хотя процесс эволюции во времени, представленный уравнением Шредингера, является непрерывным и детерминированным, поскольку знание волновой функции в один момент в принципе достаточно для расчета ее для всех будущих моментов времени, волновые функции также могут изменяться прерывисто и стохастически во время измерения . Согласно этой школе мысли, волновая функция меняется, потому что доступна новая информация. Волновая функция после измерения, как правило, не может быть известна до начала измерения, но вероятности для различных возможностей могут быть рассчитаны с использованием правила Борна . Другие, более поздние интерпретации квантовой механики, такие как реляционная квантовая механика и кбизм, также придают уравнению Шредингера статус такого рода.

Сам Шредингер предположил в 1952 году, что различные члены суперпозиции, развивающейся в соответствии с уравнением Шредингера, «не являются альтернативами, но все они действительно происходят одновременно». Это было интерпретировано как ранняя версия многомировой интерпретации Эверетта . Эта интерпретация, сформулированная независимо в 1956 году, утверждает, что все возможности, описанные квантовой теорией, одновременно возникают в мультивселенной, состоящей в основном из независимых параллельных вселенных. Эта интерпретация устраняет аксиому коллапса волновой функции, оставляя только непрерывную эволюцию по уравнению Шредингера, и поэтому все возможные состояния измеряемой системы и измерительного прибора вместе с наблюдателем присутствуют в реальной физической квантовой суперпозиции . Хотя мультивселенная детерминирована, мы воспринимаем недетерминированное поведение, управляемое вероятностями, потому что мы наблюдаем не мультивселенную в целом, а только одну параллельную вселенную в каждый момент времени. То, как именно это должно работать, было предметом многочисленных споров. Почему мы вообще должны присваивать вероятности результатам, которые наверняка произойдут в некоторых мирах, и почему вероятности должны определяться правилом Борна? Было предложено несколько способов ответа на эти вопросы в рамках многомировой структуры, но нет единого мнения относительно того, успешны ли они.

Механика Бома переформулирует квантовую механику, сделав ее детерминированной, ценой добавления силы, обусловленной «квантовым потенциалом». Он приписывает каждой физической системе не только волновую функцию, но и реальное положение, которое детерминировано развивается под действием нелокального ведущего уравнения. Эволюция физической системы всегда задается уравнением Шредингера вместе с ведущим уравнением.

См. также

• Уравнение углового дома
• Уравнение Фоккера – Планка
• Интерпретации квантовой механики
• Список вещей, названных в честь Эрвина Шредингера
• Логарифмическое уравнение Шрёдингера
• Нелинейное уравнение Шрёдингера
• уравнение Паули
• Квантовый канал
• Связь между уравнением Шредингера и формулировкой квантовой механики на основе интеграла по путям
• Картина Шрёдингера
• Распределение квазивероятностей Вигнера

Внешние ссылки

• «Уравнение Шрёдингера» . Энциклопедия математики . ЭМС Пресс . 2001 [1994].
• Квантовая кулинарная книга (PDF) и PHYS 201: Основы физики II Рамамурти Шанкара , Йельский университет OpenCourseware
• Современная революция в физике - онлайн-учебник.
• Квантовая физика I в MIT OpenCourseWare